Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.

Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) »]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
Косинус в квадрате
Косинус (cos) — это тригонометрическая функция, геометрически представляющая отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.
cos 2 (x)=cos(x)*cos(x)
Значение косинуса находится в диапазоне от -1 до +1.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата косинуса (косинуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат косинус любого угла.
Квадрат синуса, косинуса, тангенса, котангенса (альфа)
квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
sin в квадрате
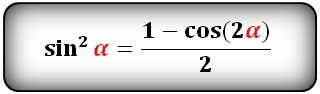
cos в квадрате
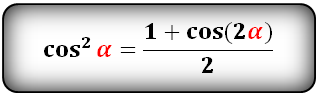
tg в квадрате
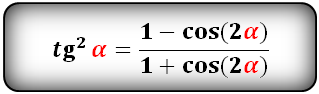
ctg в квадрате
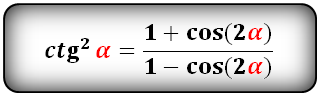
Подробности Автор: Administrator Опубликовано: 17 сентября 2011 Обновлено: 13 августа 2021
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза – сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза – это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс – «x», что не меняет сути).
Синус угла альфа (sin ∠α) – это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) – отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза – это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 – cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 – sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) < echo (Html::a(‘Войдите’, [‘/user/security/login’], [‘class’ =>”]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => ”]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else < if(!empty(Yii::$app->user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))< $name = Yii::$app->user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else < $name = ”; >echo ‘Получайте деньги за каждый набранный балл!’; > ?>–>
При правильном ответе Вы получите 8 баллов
Упростить выражение с квадратом косинуса:
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
28.01.17 / 22:14, Иван ИвановичОтветить -2
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение тригонометрических уравнений.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> –> Введите тригонометрическое уравнение
Решить уравнение
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Из определения косинуса следует, что ( -1 leqslant cos alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.
Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac<pi> <2>right] ); если a
Уравнение sin(х) = а
Из определения синуса следует, что ( -1 leqslant sin alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.
Уравнение sin х = а, где ( |a| leqslant 1 ), на отрезке ( left[ -frac<pi><2>; ; frac<pi> <2>right] ) имеет только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac<pi> <2>right] ); если а
Уравнение tg(х) = а
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.
Уравнение tg x = а для любого a имеет на интервале ( left( -frac<pi><2>; ; frac<pi> <2>right) ) только один корень. Если ( |a| geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac<pi> <2>right) ); если а
Решение тригонометрических уравнений
Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным
Решить уравнение 2 cos 2 (х) – 5 sin(х) + 1 = 0
Заменяя cos 2 (х) на 1 – sin 2 (х), получаем
2 (1 – sin 2 (х)) – 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) – 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y – 3 = 0, откуда y1 = -3, y2 = 0,5
1) sin(х) = – 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; ( x = (-1)^n text(0,5) + pi n = (-1)^n frac<pi> <6>+ pi n, ; n in mathbb )
Ответ ( x = (-1)^n frac<pi> <6>+ pi n, ; n in mathbb )
Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) – 4 = 0
Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 – sin 2 (6х)) + 4 sin(6х) – 4 = 0 => 3 sin 2 (6х) – 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 – 4y +1 =0, откуда y1 = 1, y2 = 1/3
Уравнение вида a sin(x) + b cos(x) = c
Решить уравнение 2 sin(x) + cos(x) – 2 = 0
Используя формулы ( sin(x) = 2sinfrac <2>cosfrac<2>, ; cos(x) = cos^2 frac <2>-sin^2 frac <2>) и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac <2>+ cos^2 frac <2>right) ) получаем
Поделив это уравнение на ( cos^2 frac <2>) получим равносильное уравнение ( 3 text^2frac <2>- 4 textfrac <2>+1 = 0 )
Обозначая ( textfrac <2>= y ) получаем уравнение 3y 2 – 4y + 1 = 0, откуда y1=1, y1= 1/3
В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 ) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt ):
Решить уравнение 4 sin(x) + 3 cos(x) = 5
Здесь a = 4, b = 3, ( sqrt = 5 ). Поделим обе части уравнения на 5:
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Решить уравнение sin(2х) – sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) – sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x – 1) = 0
Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х – х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0
Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) – sin 2 (x), то
cos(2x) = 1 – sin 2 (x) – sin 2 (x), cos(2x) = 1 – 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 – cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 – cos(2x)) + 2 (1 – cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0
cos^2(x) (уравнение)
Найду корень уравнения: cos^2(x)
Решение
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_ <1>= frac <sqrt- b><2 a>$$
$$w_ <2>= frac <- sqrt- b><2 a>$$
где D = b^2 – 4*a*c – это дискриминант.
Т.к.
$$a = 1$$
$$b = 0$$
$$c = 0$$
, то
Т.к. D = 0, то корень всего один.
$$w_ <1>= 0$$
делаем обратную замену
$$cos <left(x right)>= w$$
Дано уравнение
$$cos <left(x right)>= w$$
– это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = pi n + operatorname<left(w right)>$$
$$x = pi n + operatorname <left(w right)>- pi$$
Или
$$x = pi n + operatorname<left(w right)>$$
$$x = pi n + operatorname <left(w right)>- pi$$
, где n – любое целое число
подставляем w:
$$x_ <1>= pi n + operatorname <left(w_<1>right)>$$
$$x_ <1>= pi n + operatorname<left(0 right)>$$
$$x_ <1>= pi n + frac<pi><2>$$
$$x_ <2>= pi n + operatorname <left(w_<1>right)> – pi$$
$$x_ <2>= pi n – pi + operatorname<left(0 right)>$$
$$x_ <2>= pi n – frac<pi><2>$$
[spoiler title=”источники:”]
http://www.math-solution.ru/math-task/trigonometry-equality
http://www.kontrolnaya-rabota.ru/s/equal-one/any-uravnenie/expr/da8e133d680acd2bf1901c848355b5a2/
[/spoiler]
Квадрат синуса, косинуса, тангенса, котангенса (альфа)
Уравнения разложения тригонометрических функций:
квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
sin в квадрате
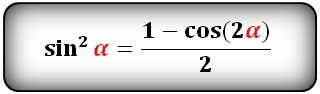
cos в квадрате
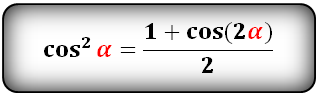
tg в квадрате
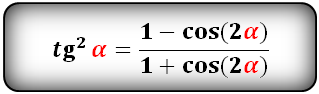
ctg в квадрате
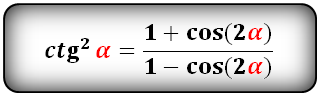
- Подробности
-
Автор: Administrator
-
Опубликовано: 17 сентября 2011
-
Обновлено: 13 августа 2021
Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Не хотят брать в 11 класс
1 ставка
Переход на домашнее обучение
1 ставка
(Вопрос по химии) Пять способов получения 2,8-диметилнонан.
1 ставка
Паникую из-за своего решения
1 ставка
Помогите с английским 21 упражнением, расставить a,an,the.
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Regin@
Ученик
(161),
закрыт
7 лет назад
Лучший ответ
Я
Ученик
(199)
14 лет назад
единица минус sin вадрат алфа
Остальные ответы
Andrey Kurgannikov
Мудрец
(12072)
14 лет назад
1-sin квадра альфа ))
ymka
Гуру
(3861)
14 лет назад
это выражение будет равно cos квадрат альфа
Похожие вопросы
Инженерный калькулятор онлайн с самыми точными расчетами!
Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.
Только корректные расчеты по всем правилам математики!
В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.
Всё для вашего удобства:
- быстрые вычисления и загрузка,
- верные расчеты по всем правилам,
- полный функционал,
- понятный интерфейс,
- адаптация под любой размер устройства
- бесплатно
- не надо ничего устанавливать,
- никакой всплывающей назойливой рекламы,
- подробная инструкция с примерами
Содержание справки:
1. Комплекс операций инженерного калькулятора
2. Инструкция по функциям инженерного калькулятора
3. Как пользоваться инженерным калькулятором – на примерах
- Как возвести в степень
- Как найти корень кубический
- Как найти корень на калькуляторе
- Как возвести в квадрат
4. Тригонометрический калькулятор онлайн – примеры
- Как произвести онлайн расчет синусов и косинусов, тангенсов
- Преобразование с кнопкой Dms и Deg на калькуляторе
- Десятичный логарифм онлайн
- Как пользоваться памятью на калькуляторе
Комплекс операций инженерного калькулятора
Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.
Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
- с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
- с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами
Инструкция по функциям инженерного калькулятора
Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн. Принцип работы с научным калькулятором такой: вводится число, с которым будет производиться вычисление, затем нажимается кнопка функции или операции, потом, если требуется, то еще цифра, например, степень, в конце – знак равенства.

- [Inv] – обратная функция для sin, cos, tan, переключает интерфейс на другие функции
- [Ln] – натуральный логарифм по основанию «e»
- [ ( ] и [ ) ] – вводит скобки
- [Int] – отображает целую часть десятичного числа
- [Sinh] – гиперболический синус
- [Sin] – синус заданного угла
- [X2] – возведение в квадрат (формула x^2)
- [n!] – вычисляет факториал введенного значения – произведение n последовательных чисел, начиная с единицы до самого введенного числа, например 4!=1*2*3*4, то есть 24
- [Dms] – переводит из десятичного вида в формат в градусы, минуты, секунды.
- [Cosh] – гиперболический косинус
- [Cos] – косинус угла
- [xy] – возведение икса в степ. игрик (формула x^y)
- [y√x] – извлечение корня в степени y из икс
- [Pi] – число Пи, выдает значение Pi для расчетов
- [tanh] – гиперболический тангенс
- [tan] – тангенс угла онлайн, tg
- [X3] – помогает возвести в степень 3, в куб (формула x^3)
- [3√x] – извлечь корень кубический
- [F – E] – переключает ввод чисел в экспоненциальном представлении и обратно
- [Exp] – позволяет вводить данные в экспоненциальном представлении.
- [Mod] – позволяет нам вычислить остаток от деления одного числа на другое
- [Log] – рассчитывает десятичный логарифм
- [10^x] – возведение десяти в произвольную степень
- [1/X] – подсчитывает обратную величину
- [e^x] – Возведение числа Эйлера в степень
- [Frac] – отсекает целую часть, оставляет дробную
- [sinh-1] – обратный гиперболический синус
- [sin-1] – арксинус или обратный синус, arcsin или 1/sin
- [deg] – перевод угла в градусах, минутах и секундах в десятичные доли градуса, подробнее
- [cosh-1] – обратный гиперболический косинус
- [cos-1] – аркосинус или обрат. косинус arccos или 1/cos
- [2*Pi] – рассчитывает число Пи, помноженное на два
- [tanh-1] – обрат. гиперболический тангенс
- [tan-1] – арктангенс или обратный тангенс, arctg
Как пользоваться MR MC M+ M- MS
Как пользоваться инженерным калькулятором – на примерах
Как возвести в степень
Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:
12 [xy] 3 [=]
12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]
Ответ: 1728
Как найти корень кубический
Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:
729 [3√x] [=]
729, [3√x] «кубический корень из икс», равенства [=]
Как найти корень на калькуляторе
Задача: Найти квадратный корень 36.
Решение: всё просто, нажимаем так:
36 [y√x] 2 [=]
36, [y√x] «корень из икса, в степени игрик», нужную нам степень 2, равно [=]
Ответ: 6
При помощи этой функции вы можете найти корень в любой степени, не только квадратный.
Как возвести в квадрат
Для возведения в квадрат онлайн вычислительная программа содержит две функции:
[xy] «икс в степени игрик», [X2] «икс в квадрате»
Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».
Например: 45 [xy] 6 [=]
Ответ: сорок пять в шестой степ. равно 8303765625
Тригонометрический калькулятор онлайн – примеры
Как произвести онлайн расчет синусов и косинусов, тангенсов
Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:
где Deg – градусы, Rad – измерение в радианах, Grad – в градах. По умолчанию включен режим расчета в градусах.
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90 [sin] [=]
Ответ: единица
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60 [cos] [=]
Решение: 0,5
Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО – арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.
Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе
[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 [Deg] [=] 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453
Десятичный логарифм онлайн
Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1 [log] [=]
Получается 0 в итоге. Для подсчета lg100 нажмем так:
100 [log] [=]
Решение: два. Как себя проверить? Что вообще такое десятичный логарифм – log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Так же вычисляется натуральный логарифм, но кнопкой [ln].
Как пользоваться памятью на калькуляторе
Существующие кнопки памяти: M+, M-, MR, MS, MC.
Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.
MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.
Пример. Внесем сто сорок пять в память программы:
145 [MR]
После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:
[MR]
На экране отобразится снова 145.
Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.
Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.
Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!
