В статье про прямоугольный треугольник посмотрели задачи связанные с синусами и косинусами из 1 части ОГЭ. Так что обязательно заглядывай.
Получается, что решить прямоугольный треугольник (найти все стороны и острые углы) можно довольно просто, зная всего лишь два элемента прямоугольного треугольника :две стороны (по теореме Пифагора) или сторону и острый угол (из определений синуса, косинуса, тангенса).
Но решить треугольник (найти все стороны и углы ) можно и произвольный, зная три элемента: три стороны, две стороны и угол, или два угла и сторону.
Для первых двух случаев в решении пользуются теоремой косинусов (вполне возможно эта тема вас поджидает уже на следующей неделе в школе, а может уже и была):
в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
- Если известны три стороны треугольника можно найти косинусы всех углов
- Если известны две стороны и угол между ними треугольника, то можно найти третью сторону.
В этом случае полезно пользоваться таблицей значений косинусов некоторых углов :
Рассмотрим решение задачи №16 из сборника Ященко (36 вариантов) на теорему косинусов :
Изобразим треугольник АВС и найдем в нем противолежащую сторону для угла АВС.
Из рисунка видно, что противолежащая сторона – это сторона АС.
Для стороны АС записываем теорему косинусов:
Подставим значения всех сторон:
Переносим все “свободные” числа (меняя знак) в левую часть равенства и считаем:
Находим косинус угла АВС, как неизвестный множитель:
Записываем ответ:
Если вы знаете того, кто готовится к ОГЭ, не забудьте поделиться с ним этой информацией. Всегда пригодится.
Продолжение следует…
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)
Теорема косинусов и синусов

О чем эта статья:
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 – 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
BC 2 = a 2 = (b cos α – c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α – 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) – 2bc cos α + c 2
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 – a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 – a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 – a 2
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 – (b × cos α) 2
- h 2 = a 2 – (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 – (b × cos α) 2 = a 2 – (c – b × cos α) 2
- a 2 = b 2 + c 2 – 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 – 2ac × cos β;
- c 2 = a 2 + b 2 – 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 – 2bc cos α
b 2 = c 2 + a 2 – 2ca cos β
c 2 = a 2 + b 2 – 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
-
Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
- Если c 2 2 + b 2 , то ∠C — острый.
Теорема косинусов
Страница содержит полную информацию о теореме косинусов, а также калькулятор, с помощью которого можно найти стороны и угол треугольника и формулу теоремы косинусов.
Теорема косинусов обобщает теорему Пифагора на произвольные плоские треугольники и устанавливает соотношение между сторонами треугольника и его углами.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Нахождение углов треугольника по заданным сторонам
Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.
От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.
Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).
Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c” />
a” />
b” />
В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.
Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)
Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.
[spoiler title=”источники:”]
http://mnogoformul.ru/teorema-kosinusov
http://planetcalc.ru/534/
[/spoiler]
Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.
Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.
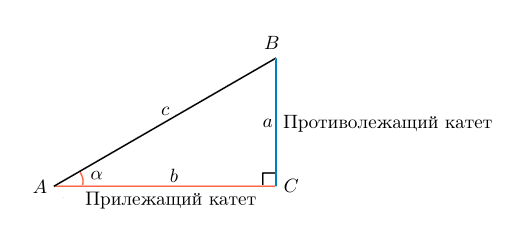
В случае с рисунком, описанным выше: cosα=bccosalpha=frac{b}{c}
Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.
Решение
Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.
a2+b2=c2a^2+b^2=c^2
62+b2=1026^2+b^2=10^2
36+b2=10036+b^2=100
b2=64b^2=64
b=8b=8
Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:
cosα=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8
Ответ
0.8
Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.
Решение
Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:
P=a+b+cP=a+b+c
25=9+4+c25=9+4+c
c=12c=12
При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:
cosα=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82
Ответ
0.820.82
Решение задач по математике от экспертов сайта Студворк!
Тест по теме “Вычисление косинуса”
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

| sin |
sin |
|
| cos |
1+tg |
cos |
| tg |
1+ctg |
sin |
| ctg |
tg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим. Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
получаем
то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
| 0 | |||||
| sin |
0 | ||||
| cos |
0 | ||||
| tg |
0 | − | |||
| ctg |
− | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и
и равными острыми углами А и

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos
и
т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол
равен
,
,
.
Найдите .

Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:

Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен
tg A =
Найдите AB.

Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A =
Найдите AH.

Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно
откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.

Решение:
Так как sin A = тогда
c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
=
получим
тогда BH = = 0,5,
AH = AB – BH = 18 – 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.

Решение:
Так как для АВС:
A =
sin В =
а для ВНС: sin В =
=
, откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:
По определению sin A= =
=
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A =
= 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:
По определению sin A = =
=
cos A =
=
=
тогда tg A = который найдем из
BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A =
Найдите АН.

Решение:
По определению tg A=
Для BHC:
, значит
СН =
Для АHC: tg A=
то
AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A =
Найдите АВ.
Решение:

Так как cos В = = sin A =
Из СВН имеем cos В =
=
тогда ВС =
В АВС имеем sinA =
=
тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:

Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A =
получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит
или
k = тогда
АС =
;
АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда
АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А =
= cos C =
Для АНВ: sin А =
=
то
=
АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:

В прямоугольном АСЕ sin А =
значит
= 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:

A-общий,
),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A =
то есть
АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A =
AC = 10
Найдите АВ.
Решение:

1-й способ.
Поскольку sin A =
то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то
откуда АВ =
= 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:

Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30
АВ = 2
Найдите высоту CH.
Решение:

Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС =
АВ =
В BHC:
то
следовательно, ВН =
BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2,
Найдите АH.
Решение:

Из АВС найдем ВС =
АВ = 1 (по свойству катета, лежащего против угла 30
),
то
Из ВСН:
то
следовательно,
ВН = ВС =
АН = АВ — НВ = 2 – = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Как находить косинус в треугольнике
Нередко в геометрических (тригонометрических) задачах требуется найти косинус угла в треугольнике, потому что косинус угла позволяет однозначно определить величину самого угла.

Инструкция
Чтобы найти косинус угла в треугольнике, длины сторон которого известны, можно воспользоваться теоремой косинусов. Согласно этой теореме, квадрат длины стороны произвольного треугольника равняется сумме квадратов двух его других сторон без удвоенного произведения длин этих сторон на косинус угла между ними:
а?=b?+c?-2*b*c*соs?, где:
а, b, с – стороны треугольника (точнее их длины),
? – угол, противоположный стороне а (его величина).
Из приведенного равенства легко находится соs?:
соs?=( b?+c?-а? )/(2*b*c)
Пример 1.
Имеется треугольник со сторонами а, b, с, равными 3, 4, 5 мм, соответственно.
Найти косинус угла, заключенного между большими сторонами.
Решение:
По условию задачи имеем:
а=3,
b=4,
с=5.
Обозначим противоположный стороне а угол через ?, тогда, согласно выведенной выше формуле, имеем:
соs?=(b?+c?-а? )/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40=32/40=0,8
Ответ: 0,8.
Если треугольник прямоугольный, то для нахождения косинуса угла достаточно знать длины всего двух любых сторон (косинус прямого угла равен 0).
Пусть имеется прямоугольный треугольник со сторонами а, b, с, где с – гипотенуза.
Рассмотрим все варианты:
Пример 2.
Найти соs?, если известны длины сторон а и b (катеты треугольника)
Воспользуемся дополнительно теоремой Пифагора:
c?=b?+а?,
с=v(b?+а?)
соs?=(b?+c?-а? )/(2*b*c)=(b?+b?+а?-а?)/(2*b*v(b?+а?))=(2*b?)/(2*b*v(b?+а?))=b/v(b?+а?)
Чтобы проверить правильность полученной формулы, подставим в нее значения из примера 1, т.е.
а=3,
b=4.
Проделав элементарные вычисления, получаем:
соs?=0,8.
Аналогично находится косинус в прямоугольном треугольнике в остальных случаях:
Пример 3.
Известны а и с (гипотенуза и противолежащий катет), найти соs?
b?=с?-а?,
b=v(c?-а?)
соs?=(b?+c?-а? )/(2*b*c)=(с?-а?+с?-а?)/(2*с*v(с?-а?))=(2*с?-2*а?)/(2*с*v(с?-а?))=v(с?-а?)/с.
Подставляя значения а=3 и с=5 из первого примера, получаем:
соs?=0,8.
Пример 4.
Известны b и с (гипотенуза и прилежащий катет).
Найти соs?
Произведя аналогичные (показанные в примерах 2 и 3 преобразования), получим, что в этом случае косинус в треугольнике вычисляется по очень простой формуле:
соs?=b/с.
Простота выведенной формулы объясняется элементарно: фактически, прилежащий к углу ? катет является проекцией гипотенузы, поэтому его длина равна длине гипотенузы, умноженной на соs?.
Подставляя значения b=4 и с=5 из первого примера, получим:
соs?=0,8
Значит, все наши формулы верны.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
