810°=360°*2+90°=720°+90° значит надо найти cos 810°=cos90°= 0
810 °это 2 полных оборота по 360 градусов и еще 90 градусов
Отмена
Марина Подкидкина
Отвечено 26 сентября 2019
-
Комментариев (0)
Добавить
Отмена
810°=360°*2+90°=720°+90° значит надо найти cos 810°=cos90°= 0
810 °это 2 полных оборота по 360 градусов и еще 90 градусов
parus77_zn
17 Май, 18

Тригонометрический круг со всеми значениями
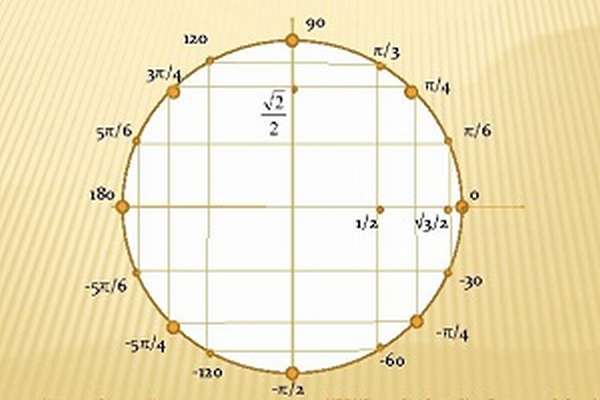
Тригонометрический круг один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.
Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.
Тригонометрическая окружность
Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.
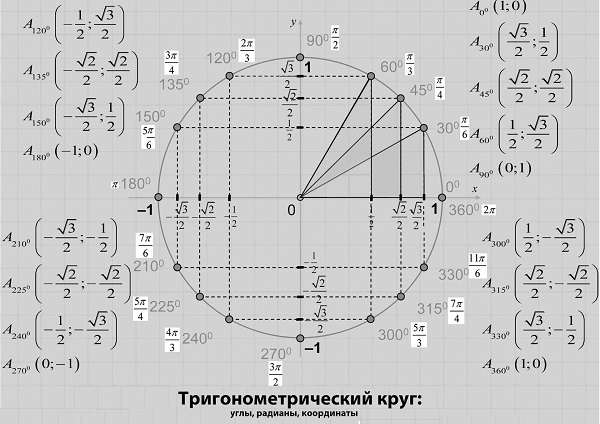
Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.
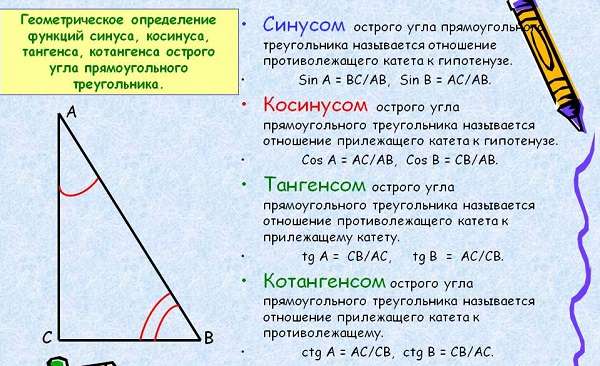
Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
Построение единичной окружности
Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.
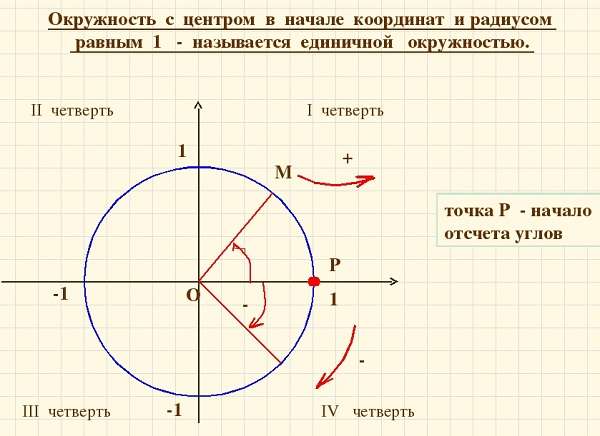
Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.
Сделать перевод этих показателей просто полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
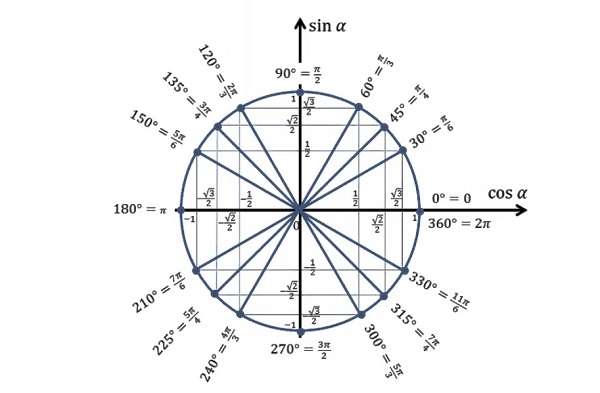
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° значения углов от 0 до ∏/2,
- от 90 до 180° значения углов от ∏/2 до ∏,
- от 180 до 270° от ∏ до 3*∏/2,
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.
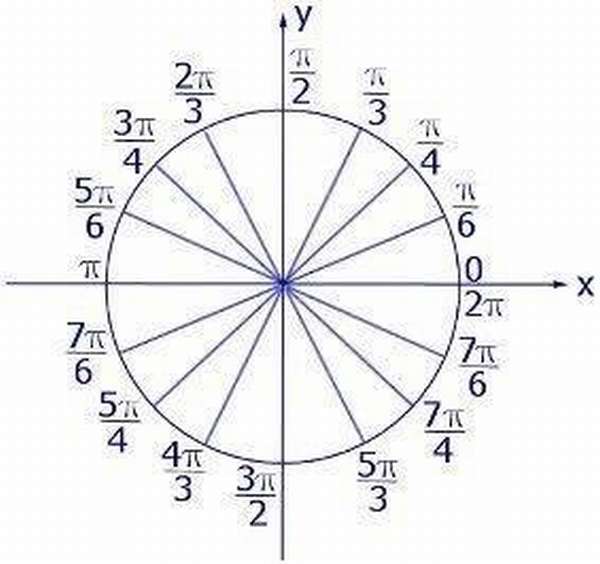
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Перевод углов из градусов в радианы
Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.
Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:
1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956
В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:
1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.

Косинус, синус, тангенс, котангенс на тригонометрической окружности
Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.
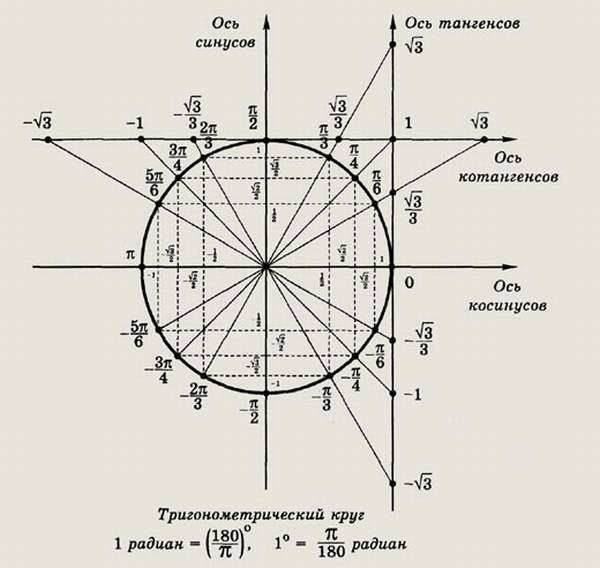
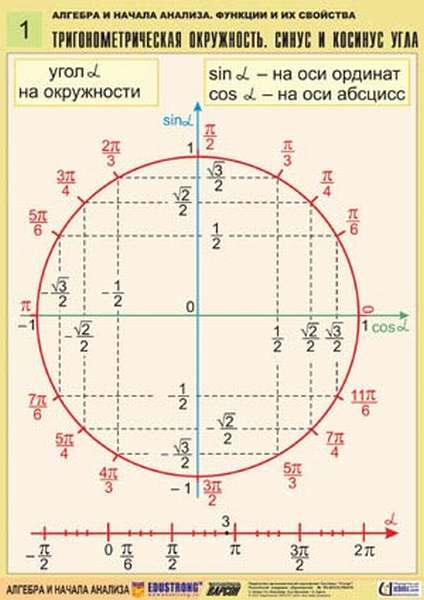
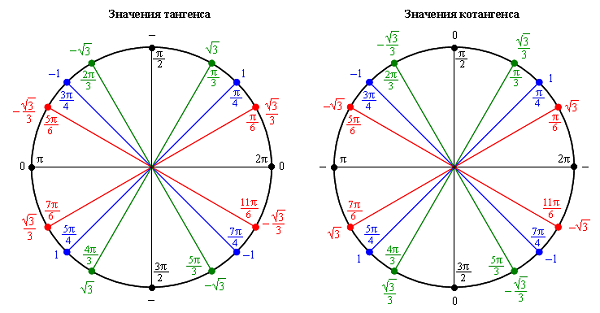
Заключение
В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии “на пальцах”.
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
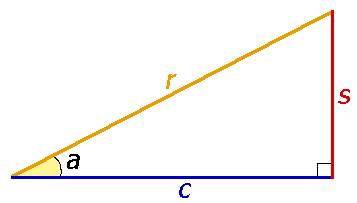
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|
| sin | 0 | 1 | √3 | – |
| ctg | – | √3 | 1 |
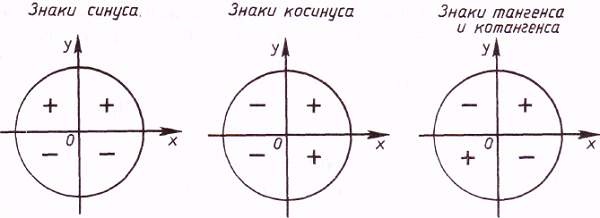
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. Единичная окружность
О чем эта статья: 10 класс, ЕГЭ/ОГЭ Статья находится на проверке у методистов Skysmart. Единичная окружность в тригонометрииВсе процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение. Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице. Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра. Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью. Поясним, как единичная окружность связана с тригонометрией. В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности. Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA. Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности. Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так: Радиан — одна из мер для определения величины угла. Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса. Число радиан для полной окружности — 360 градусов. Длина окружности равна 2πr, что превышает длину радиуса в 2π раза. Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан. Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса. Уравнение единичной окружности При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество: Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам. [spoiler title=”источники:”] http://matematika.club/articles/trigonometry/ http://skysmart.ru/articles/mathematic/edinichnaya-okruzhnost [/spoiler] |
Свойства натурального числа 810, 0x00032A, 0x32A: 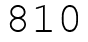
Рейтинг 0 из 10,
оценок: 0.
Системы счисления, перевод в систему счисления
Десятичное число 810
-
- 810 в шестнадцатеричной системе счисления
- 32A
-
- 810 в двоичной системе счисления
- 1100101010
-
- 810 в восьмеричной системе счисления
- 1452
Шестнадцатеричное число 32A
-
- 32A в десятичной системе
- 810
-
- 32A в двоичной системе
- 1100101010
-
- 32A в восьмеричной системе
- 1452
Двоичное число 1100101010
-
- 1100101010 в десятичной системе
- 810
-
- 1100101010 в шестнадцатеричной системе
- 32A
-
- 1100101010 в восьмеричной системе
- 1452
Восьмеричное число 1452
-
- 1452 в десятичной системе
- 810
-
- 1452 в шестнадцатеричной системе
- 32A
-
- 1452 в двоичной системе
- 1100101010
Основные арифметические и алгебраические свойства
-
- Число 810 на русском языке, number in Russian, число 810 прописью:
- восемьсот десять
-
- Четность
- Четное число 810
-
- Разложение на множители, делители числа 810
- 2, 3, 3, 3, 3, 5, 1
-
- Простое или составное число
- Составное число 810
-
- Числа делящиеся на целое число 810
- 1620, 2430, 3240, 4050, 4860, 5670, 6480, 7290
-
- Число 810 умноженное на число два
- 1620
-
- 810 деленное на число 2
- 405
-
- Список 8-ми простых чисел перед числом
- 809, 797, 787, 773, 769, 761, 757, 751
-
- Сумма десятичных цифр
- 9
-
- Количество цифр
- 3
-
- Десятичный логарифм 810
- 2.9084850188786
-
- Натуральный логарифм 810
- 6.6970342476665
-
- Это число Фибоначчи?
- Нет
-
- Число на 1 больше числа 810,
следующее число - число 811
- Число на 1 больше числа 810,
-
- Число на 1 меньше числа 810,
предыдущее число - 809
- Число на 1 меньше числа 810,
Степени числа, корни
-
- 810 во второй степени (в квадрате)
(функция x в степени 2 – x²) - 656100
- 810 во второй степени (в квадрате)
-
- В третьей степени (в кубе, 810 в степени 3, x³) равно
- 531441000
-
- Корень квадратный из 810
- 28.460498941515
-
- Корень кубический из числа 810 =
- 9.3216975178616
Тригонометрические функции, тригонометрия
-
- Синус, sin 810 градусов, sin 810°
- 1
-
- Косинус, cos 810 градусов, cos 810°
- 0
-
- Тангенс, tg 810 градусов, tg 810°
- 1.814582150355E+15
-
- Синус, sin 810 радиан
- -0.50631365209994
-
- Косинус, cos 810 радиан
- 0.86234939885015
-
- Тангенс, tg 810 радиан равно
- -0.5871328405575
-
- 810 градусов, 810° =
- 14.137166941154 радиан
-
- 810 радиан =
- 46409.581405597 градуса, 46409.581405597°
Контрольные суммы, хэши, криптография
-
- MD-5 хэш(810)
- b6edc1cd1f36e45daf6d7824d7bb2283
-
- CRC-32, CRC32(810)
- 901601828
-
- SHA-256 hash, SHA256(810)
- 5d85be4cc5af40a7cf2c4f0818d92689c185fdea6566745ef26305d80413f483
-
- SHA1, SHA-1(810)
- a1496d4ad0a359b6fe93d819e4a2141bd9d9ac35
-
- ГОСТ Р 34.11, GOST R 34.11-94, GOST(810)
- 9057aad3749a97c4df87bca4169b218297765473776426e42dc561a3c4b2f299
-
- Base64
- ODEw
Языки программирования
-
- C++, CPP, C значение 810
- 0x00032A, 0x32A
-
- Delphi, Pascal значение числа 810
- $00032A
Дата и время
-
- Конвертация UNIX timestamp 810 в дату и время
-
- UTC
- четверг, 1 января 1970 г., 0:13:30 GMT
- в Москве, Россия
- четверг, 1 января 1970 г., 3:13:30 Московское стандартное время
- в Лондоне, Великобритания
- четверг, 1 января 1970 г., 1:13:30 GMT+01:00
- в Нью-Йорке, США
- среда, 31 декабря 1969 г., 19:13:30 Восточно-американское стандартное время
Интернет
-
- Конвертация в IPv4 адрес Интернет
- 0.0.3.42
-
- 810 в Википедии:
- 810
Другие свойства числа
-
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/810
-
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/x32A
-
- Номер телефона
- 8-10
-
- Телефонный код страны
- +810
Цвет по числу 810, цветовая гамма
-
- html RGB цвет 810, 16-ричное значение
- #00032A – (0, 3, 42)
-
- HTML CSS код цвета #00032A
- .color-mn { color: #00032A; }
.color-bg { background-color: #00032A; }
Цвет для данного числа 810
Здесь вы можете изменить составляющую цвета для данного числа 810 или цвета 00032A:



