В оригинале надо было найти углы, но пару раз выкладывались задачи с арксинусом и как-то «не зашли» они, этот раз без них.
Задача простая — найти косинусы углов. Как и в любом вопросе, в этом тоже есть подсказка — или теорема косинусов, или теорема синусов, или тригонометрические функции в прямоугольном треугольнике. Последнее более вероятно. Ну а дальше несколько подсказок!
Биссектрисы. Какие треугольники отсекают биссектрисы от этой трапеции и почему они «такие»? Если с этим разберёмся — можно выразить через одну переменную сперва меньшее основание, а потом и большее. Ну а чтобы найти косинусы углов — можно сперва выполнить перенос одной боковой стороны к другой. Там сперва нужно будет сделать выводы. И готово.
Условие
Отношение оснований трапеции равно 3 : 2, а отношение боковых сторон равно 5 : 3 . Точка пересечения биссектрис углов при большем основании трапеции лежит на меньшем основании. Найдите косинусы углов трапеции.
Просто? Попробуйте эти:
💀 Площадь трапеции через основания и угол между боковыми сторонами
☠️ Площадь прямоугольной трапеции и пропорциональные отрезки
👻 Найти все углы трапеции
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,939 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Сообщения без ответов | Активные темы
Найти косинус угла в трапеции – помогите, не получается
Модераторы: Prokop, mad_math
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Toma |
|
|||
|
Если в трапеции [math]ABCD[/math] ([math]AB||DC[/math] ) [math]AB=6,~BC=3,~CD=4,~DA=2[/math], найти косинуса угла [math]C[/math]. Заранее пребольшое спасибо!
|
|||
| Вернуться к началу |
|
|||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти косинус угла между векторами
в форуме Аналитическая геометрия и Векторная алгебра |
Ilia213 |
2 |
185 |
19 дек 2022, 20:35 |
|
Найти косинус третьего угла треугольника
в форуме Геометрия |
Onex |
6 |
985 |
19 сен 2013, 15:49 |
|
Как найти косинус угла у вершины треугольника С ?
в форуме Аналитическая геометрия и Векторная алгебра |
Leonor19 |
2 |
429 |
01 окт 2016, 13:56 |
|
Найти косинус, синус и тангенс угла
в форуме Аналитическая геометрия и Векторная алгебра |
Cris_21 |
2 |
457 |
01 мар 2017, 02:15 |
|
Найти синус, косинус и котангенс угла
в форуме Тригонометрия |
nikpasternak |
3 |
413 |
20 мар 2018, 23:58 |
|
Косинус угла AOB
в форуме Алгебра |
belinum |
1 |
346 |
25 окт 2013, 19:15 |
|
Косинус половинного угла
в форуме Тригонометрия |
III_X |
12 |
1065 |
30 ноя 2013, 14:48 |
|
Косинус угла между сторонами
в форуме Аналитическая геометрия и Векторная алгебра |
Ket |
1 |
762 |
05 фев 2014, 06:19 |
|
Косинус угла между векторами p q
в форуме Векторный анализ и Теория поля |
proclown3 |
2 |
125 |
18 окт 2022, 21:35 |
|
Найдите косинус угла между векторами
в форуме Аналитическая геометрия и Векторная алгебра |
ivan kumaev |
1 |
82 |
20 дек 2022, 19:56 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.
Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.
- Угол трапеции при основании через высоту и прилегающую
боковую сторону - Угол трапеции через нижнее основание, боковую сторону и
диагональ - Угол равнобедренной трапеции через нижнее основание,
среднию линию и боковую сторону - Угол равнобедренной трапеции через среднию линию, верхнее
основание и боковую сторону - Острый угол при нижнем основании прямоугольной трапеции
через высоту и два основания - Острый угол при нижнем основании прямоугольной трапеции
через два основания и боковую сторону
Угол трапеции при основании через высоту и прилегающую боковую сторону
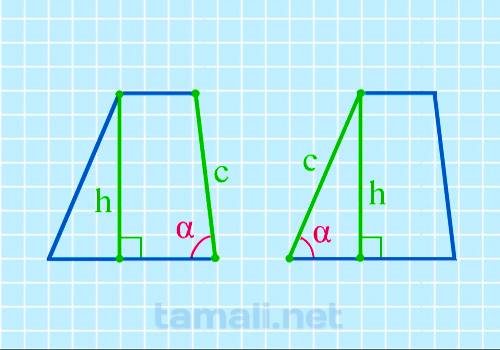
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы
sin α = h/с
где: h — высота трапеции, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.
Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции
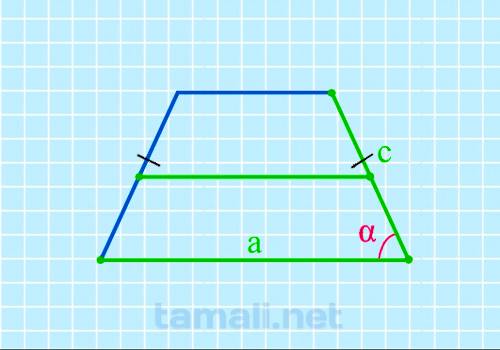
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:
cos α = (2a-2m) / 2c
где а — нижнее основание, m — средняя линия, с — боковая сторона.
Цифр после
запятой:
Результат в:
Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.
Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали
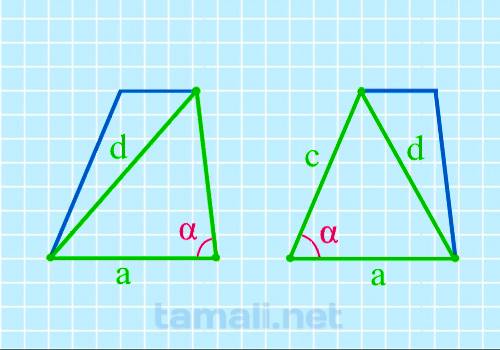
Если известны эти величины, воспользуемся формулой:
cos α= (a²+c²-d²) / 2ac
где а-нижнее основание, d-диагональ, с-боковая сторона.
Цифр после
запятой:
Результат в:
Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.
Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции
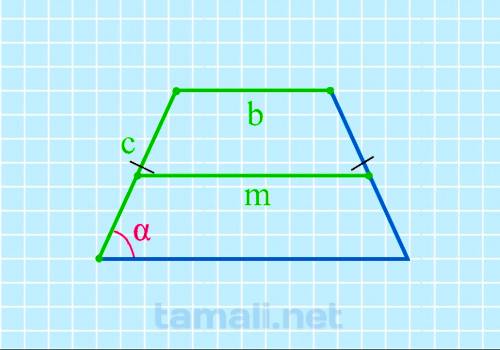
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:
cos α = (2m-2b) / 2c
где m — средняя линия, b — верхнее основание, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º
Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции
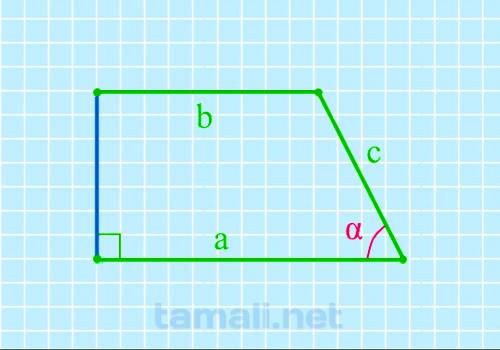
Находится по формуле
cos α = (a — b) / c
где a,b — основания, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º
Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции
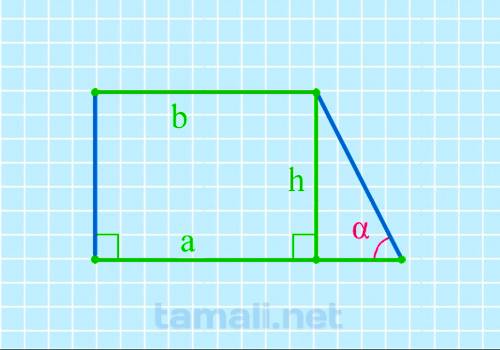
При известных указанных величинах воспользуемся следующей формулой:
tg(α) = h / (a-b)
где h — высота, a,b — верхнее и нижнее основания.
Цифр после
запятой:
Результат в:
Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.
Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.
Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.
Геометрия,
вопрос задал Iizziknya,
5 лет назад
Ответы на вопрос
Ответил siestarjoki
0
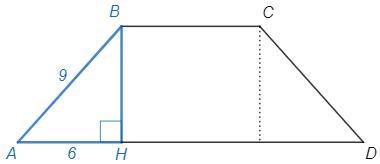
Опустим высоту BH.
Равнобедренная трапеция, AH= (AD-BC)/2 =6
cosA= AH/AB =6/9 =2/3
sinA= √(1 -cosA^2) =√5/3
tgA= sinA/cosA =√5/2
ctgA= 1/tgA =2/√5
Приложения:
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Алгебра,
8 месяцев назад
Cрочно! Заранее Спасибо! Даю 35 баллов.
Химия,
8 месяцев назад
Оксид елементу з вищою валентністю ІІІ групи головної підгрупи має відносну молекулярну масу 276. Визначте, що це за елемент.
Геометрия,
5 лет назад
Все условия задач на картинке…
История,
5 лет назад
Городские восстания (соляной и медный бунты).причины и итоги КРАТКО СРОЧНО дам 25 баллов.
История,
6 лет назад
Что такое АКАДЕМИЗМ, РАССКОВИЗАНТИЙСКИЙ СТИЛЬ, ЖАНДАРМЕРИЯ, ПРОМЫШЛЕНЫЙ ПЕРЕВОРОТ.
История,
6 лет назад
Запишите термины а) характеризующие политическую власть и ее органы. б) характеризующие жизнь в Нидерландах и их освободительную войну против испанского владычества.




