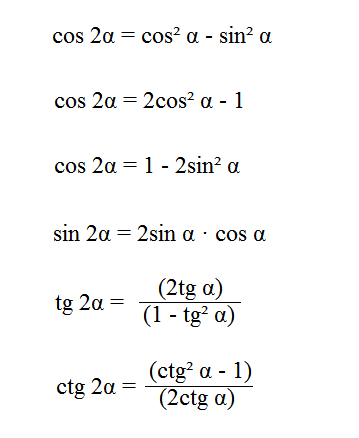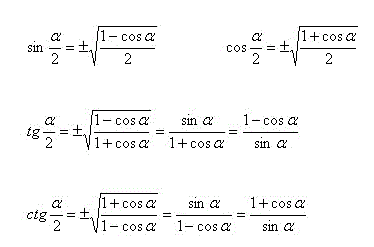Как найти косинус альфа пополам

Формулы половинного угла (аргумента) представляют собой противоположность формулам двойного угла , так как они выражают синус, косинус, тангенс и котангенс угла α2 при помощи тригонометрических функций угла α. В статье раскрыты формулы половинного угла и добавлены их доказательства с примерами решений.

Список формул половинного угла

Стандартные формулы половинного угла:

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы для sin и cos половинного угла справедливы при любом значении заданного угла α. Формулу для tg любого угла αопределяет tgα2, значение угла α≠π+2π·z при z равном любому целому числу ( выражение 1+cosα с таким же значением α не должно принимать значение 0). Формула ctg угла считается справедливой для любого угла α, где половинный угол имеет место быть, α≠2π·z.

Самые значимые формулы половинного угла для квадратов тригонометрических функций выводятся через положительное или отрицательное значение арифметического квадратного корня. Имеем формулы половинного угла:

sinα2=±1-cosα2, cosα2=±1+cosα2, tgα2=±1-cosα1+cosα, ctgα2=±1+cosα1-cosα

Знак «-» указывает, что тригонометрическая функция принадлежит определенной четверти угла α2.

Применим формулы на практике.

Доказательство формул половинного угла

Доказательство формул половинного угла основывается на формулах cos двойного угла cosα=1-2·sin2α2 и cosα=2·cos2α2-1. Упростив первое выражение по sin2α2, получим саму формулу половинного угла sin2α2=1-cosα2, второе выражение по cos2α2 получим cos2α2=1+cosα2.

Чтобы доказать формулы половинного угла для tg и ctg угла α2, необходимо применить основные тригонометрические тождества tgα2=sinα2cosα2 и ctgα2=cosα2sinα2, к ним необходимо добавить формулы половинного угла cos и sin, которые доказали выше. При подстановке получим выражения, имеющие вид:

tg2α2=sin2α2cos2α2=1-cosα21+cosα2=1-cosα1+cosα;ctg2α2=cos2α2sin2α2=1-cosα21+cosα2=1+cosα1-cosα;

Все формулы половинного угла были доказаны.

Примеры использования

Покажем применение формул половинного угла при решении примера.

Применяя формулу половинного угла, стоит учитывать тот факт, что угол может быть не явного вида α2 и α, а потребует дальнейшего приведения к стандартному виду. Главное условие – нахождение аргумента в правой части формул половинного угла было в 2 раза больше, чем в левой. Иначе применение формулы будет невозможно.

Если формула позволит записывать данное равенство таким образом sin27α=1-cos14α2 или sin2 5α17=1-cos10α172, то формула будет применима.

Для правильного преобразования и применения формул половинного аргумента необходимо досконально изучить свойства тригонометрических функций. Не любое выражение поддается такому преобразованию в тригонометрии. Необходимо внимательно следить за значениями углов тригонометрических функций и их нахождение в четвертях для определения знака для выражения.

Все формулы половинного угла в тригонометрии:

Формулы половинного угла (половинного аргумента) – это часть от всех основных тригонометрических формул. Они выражают функции синус, косинус, тангенс, котангенс угла `frac{alpha}2` через эти ж функции аргумента `alpha`. Они, можно сказать, противоположны формулам двойного угла. Ниже приведены все формулы половинных углов, их вывод, а также примеры решения задач с их использованием.

Список всех формул половинного угла

Их можно встретить записанными в двух видах. В первом каждая из тригонометрических функций выражается через радикал:

`sin frac alpha 2=pm sqrt{frac {1-cos alpha}2}`
`cos frac alpha 2=pm sqrt{frac {1+cos alpha}2}`
`tg frac alpha 2=pm sqrt{frac {1-cos alpha}{1+cos alpha}}=` `frac {sin alpha}{1+cos alpha}=frac {1-cos alpha}{sin alpha}`
`ctg frac alpha 2=pm sqrt{frac {1+cos alpha}{1-cos alpha}}=` `frac {sin alpha}{1-cos alpha}=frac {1+cos alpha}{sin alpha}`

Знак «+» или «-» перед корнями зависит от того, в какую из координатных четвертей попадает угол `frac{alpha}2`.

Во втором варианте имеем дело с квадратами тригонометрических функций половинного угла:

`sin^2 frac alpha 2=frac {1-cos alpha}2`
`cos^2 frac alpha 2=frac {1+cos alpha}2`
`tg^2 frac alpha 2=frac {1-cos alpha}{1+cos alpha}`
`ctg^2 frac alpha 2=frac {1+cos alpha}{1-cos alpha}`

Формула синуса и косинуса половинного угла имеет место при любом угле `alpha`.

Формула тангенса половинного угла справедлива для тех углов `alpha`, при которых определен `tg frac alpha 2`, то есть при ` alphanepi+2pi n, n in Z`.

Формула котангенса выполняется для тех `alpha`, при которых определен `ctg frac alpha 2`, то есть при ` alphane 2pi n, n in Z`.

С помощью следующего набора формул можно выразить каждую из тригонометрических функций угла `alpha` через тангенс половинного угла.

`sin alpha= frac{2tgfrac{alpha}{2}}{1 + tg^{2}frac{alpha}{2}},` ` alphane pi +2pi n, n in Z`
`cos alpha= frac{1 — tg^{2}frac{alpha}{2}}{1 + tg^{2}frac{alpha}{2}},` ` alpha ne pi +2pi n, n in Z`
`tg alpha= frac{2tgfrac{alpha}{2}}{1 — tg^{2}frac{alpha}{2}},` ` alpha ne pi +2pi n, n in Z,` ` alpha ne frac{pi}{2}+ pi n, n in Z`
`ctg alpha = frac{1 — tg^{2}frac{alpha}{2}}{2tgfrac{alpha}{2}},` ` alpha ne pi n, n in Z,` `alpha ne pi + 2pi n, n in Z`

Вывод формул половинного угла

Формула косинуса и синуса половинного угла выводится из формул косинуса двойного угла `cos 2alpha=1-2 sin^2 alpha` и `cos 2alpha=2 cos^2 alpha-1`. Запишем их в следующем виде: `cos alpha=1-2 sin^2 frac alpha 2` и `cos alpha=2 cos^2 frac alpha 2-1`. Выразив из первого равенства ` sin frac alpha 2` получим `sin frac alpha 2=pm sqrt{frac {1-cos alpha}2}`. Аналогично разрешив второе равенство относительно ` cos frac alpha 2` в результате будем иметь `cos frac alpha 2=pm sqrt{frac {1+cos alpha}2}`.

Формулы тангенса и котангенса половинного угла можно вывести, используя определения этих функций в виде `tg frac alpha 2=frac{sinfrac alpha 2}{cos frac alpha 2}` и `ctg frac alpha 2=frac{cos frac alpha 2}{sin frac alpha 2}`, а также две уже доказанные выше формулы для синуса и косинуса.

В результате будем иметь: `tg frac alpha 2=frac{sinfrac alpha 2}{cos frac alpha 2}=` `frac{pm sqrt{frac {1-cos alpha}2}}{pm sqrt{frac {1+cos alpha}2}}=` `pm sqrt{frac {1-cos alpha}{1+cos alpha}}` и `ctg frac alpha 2=frac{cosfrac alpha 2}{sin frac alpha 2}=` `frac{pm sqrt{frac {1+cos alpha}2}}{pm sqrt{frac {1-cos alpha}2}}=` `pm sqrt{frac {1+cos alpha}{1-cos alpha}}`.

Примеры использования при решении задач

Пример 1. Найти `cos 15^circ`, если известно, что `cos 30^circ=frac{sqrt3}2`.

Решение. Формула половинного угла для тригонометрической функции косинус имеет вид `cos^2 frac alpha 2=frac {1+cos alpha}2`. Подставив известные значения, имеем `cos^2 15^circ=frac {1+cos 30^circ}2=` `frac{1+frac{sqrt3}2}2=frac{2+sqrt3}4`. Имея значение `cos^2 15^circ`, найдем `cos 15^circ`. Поскольку угол 15 градусов лежит в первой координатной четверти, а косинус в этой четверти имеет знак «+», то `cos 15^circ=sqrt{frac{2+sqrt3}4}=` `frac{sqrt{2+sqrt3}}2`.

Ответ. `cos 15^circ=frac{sqrt{2+sqrt3}}2`.

Пример 2. Вычислить значение выражения `4cos frac {alpha}2+2cos alpha+5`, если `cos alpha=frac {1}8`.

Решение. Используя ту же формулу, что и в первом примере (`cos frac alpha 2=pm sqrt{frac {1+cos alpha}2}`) и известное значение косинуса, упростим выражение: `4sqrt{frac {1+cos alpha}2}+2cos alpha+5=4sqrt{frac {1+frac {1}8}2}+2 cdot frac {1}8+5=` `4sqrt{frac {9}16}+frac{1}4+5=8frac{1}4`.

Ответ. `4cos frac {alpha}2+2cos alpha+5=8frac{1}4`.

Еще несколько примеров с подробным объяснением посмотрите на видео:

В большинстве случаев формулы половинного угла используются при преобразовании тригонометрических выражений.

Материалы по теме:

• Тригонометрические формулы: косинус, синус и тангенс двойного угла
• Формулы понижения степени в тригонометрии: вывод и примеры
• Все формулы по тригонометрии
• Формулы приведения тригонометрических функций

Косинус половинного угла, формула

Данная формула позволяет найти косинус половинного угла зная косинус этого угла:

[
cosbigg(frac{α}{2}bigg) = sqrt{frac{1 + cos(α)}{2}}
]

Смотрите также: Синус половинного угла

Вычислить, найти косинус половинного угла, по формуле (1)

α° (градусов)

α´ (минут)

α˝ (секунд)

нажмите кнопку для расчета

Косинус половинного угла, формула	стр. 223

Что такое формулы половинного угла в тригонометрии

Перечислим их:

• (sin^2left(fracalpha2right)=frac{1-cosleft(alpharight)}2), где (alpha) — любой угол;
• (cos^2left(fracalpha2right)=frac{1+cosleft(alpharight)}2), где (alpha) — любой угол;
• (tan^2left(fracalpha2right)=frac{1-cosleft(alpharight)}{1+cosleft(alpharight)}), где (alphaneqmathrmpi+2mathrmpitimesmathrm z)  (z — любое целое число);
• (cot^2left(fracalpha2right)=frac{1+cosleft(alpharight)}{1-cosleft(alpharight)}), где (alphaneq2mathrmpitimesmathrm z) (z — любое целое число).

Все формулы половинного угла даны для вычисления квадрата функции. Выражение решается до конца с помощью нахождения арифметического квадратного корня, т.е.:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

• (sinleft(fracalpha2right)=pmsqrt{frac{1-cosleft(alpharight)}2});
• (cosleft(fracalpha2right)=pmsqrt{frac{1+cosleft(alpharight)}2});
• (tanleft(fracalpha2right)=pmsqrt{frac{1-cosleft(alpharight)}{1+cosleft(alpharight)}});
• (cotleft(fracalpha2right)=pmsqrt{frac{1+cosleft(alpharight)}{1-cosleft(alpharight)}}).

Знак, стоящий перед ответом, обозначает координатную четверть, в которой находится угол (fracalpha2. )

График:

Доказательство формул половинного угла

Данное доказательно основано на формулах косинуса двойного угла:

(cosleft(alpharight)=1-2timessin^2fracalpha2;)

(cosleft(alpharight)=2timescos^2(fracalpha2)-1.)

И основных тригонометрических тождествах:

(tanleft(fracalpha2right)=frac{sinleft({displaystylefracalpha2}right)}{cosleft({displaystylefracalpha2}right)};)

(cotleft(fracalpha2right)=frac{cosleft(fracalpha2right)}{sinleft(fracalpha2right)}.)

Вывод с доказательством через синус, косинус, тангенс и котангенс

Для доказательства формул синуса и косинуса половинного угла используем формулы косинуса двойного угла.

Решим первое равенство относительно (sin^2left(fracalpha2right)) для выведения синуса

Решим второе уравнение относительно (sin^2left(fracalpha2right)) для выведения косинуса.

Перейдем к приведению тангенса и котангенса половинного угла через тригонометрические тождества.

(tan^2left(fracalpha2right)=frac{sin^2left({displaystylefracalpha2}right)}{cos^2left(fracalpha2right)}=frac{displaystylefrac{1-cosleft(alpharight)}2}{displaystylefrac{1+cos(alpha)}2}=frac{1-cosleft(alpharight)}{1+cosleft(alpharight)} )

(cot^2left(fracalpha2right)=frac{cos^2left({displaystylefracalpha2}right)}{sin^2left(fracalpha2right)}=frac{displaystylefrac{1+cosleft(alpharight)}2}{displaystylefrac{1-cos(alpha)}2}=frac{1+cosleft(alpharight)}{1-cosleft(alpharight)})

ЧТД.

Пример задачи с решением

Задача 1

Косинус угла в 30 градусов равен (frac{sqrt3}2.)

Найдите косинус угла в 15 градусов.

Решение

Воспользуемся формулой половинного угла для косинуса. Получим:

(cos^2left(15^circright)=frac{1+cosleft(30^circright)}2=frac{1+{displaystylefrac{sqrt3}2}}2=frac{2+sqrt3}4.)

Угол в 15 градусов находится в первой координатной четверти. Следовательно, его косинус будет являться положительным. 

Ответ:

(cosleft(15^circright)=sqrt{frac{2+sqrt3}4}=frac{sqrt{2+sqrt3}}2.)

Half Angle formulas are used to find various values of trigonometric angles such as for 15°, 75°, and others, they are also used to solve various trigonometric problems.

Several trigonometric ratios and identities help in solving problems of trigonometry. The values of trigonometric angles 0°, 30°, 45°, 60°, 90°, and 180° for sin, cos, tan, cosec, sec, and cot are determined using a trigonometry table. Half-Angle formulas are widely used in mathematics, let’s learn about them in detail in this article. 

Half-Angle Formulae

For finding the values of angles apart from the well-known values of 0°, 30°, 45°, 60°, 90°, and 180°. Half angles are derived from double angle formulas and are listed below for sin, cos, and tan:

• sin (x/2) = ± [(1 – cos x)/ 2]^1/2
• cos (x/2) = ± [(1 + cos x)/ 2]^1/2
• tan (x/ 2) = (1 – cos x)/ sin x

Trigonometric identities of double-angle formulas are useful for the derivation of half-angle formulas.

Half Angle Identities

Half-angle identities for some popular trigonometric functions are,

• Half Angle Formula of Sin,

sin A/2 = ±√[(1 – cos A) / 2]

• Half Angle Formula of Cos, 

cos A/2 = ±√[(1 + cos A) / 2]

• Half Angle Formula of Tan,

tan A/2 = ±√[1 – cos A] / [1 + cos A]

tan A/2 = sin A / (1 + cos A)

tan A/2 = (1 – cos A) / sin A

Half Angle Formulas Derivation Using Double Angle Formulas

Half-Angle formulas are derived using double-angle formulas. Before learning about half-angle formulas we must learn about Double-angle in Trigonometry, most commonly used double-angle formulas in trigonometry are:

• sin 2x = 2 sin x cos x
• cos 2x = cos² x – sin² x
             = 1 – 2 sin²x
             = 2 cos²x – 1
• tan 2x = 2 tan x / (1 – tan²x)

Now replacing x with x/2 on both sides in the above formulas we get

• sin x = 2 sin(x/2) cos(x/2)
• cos x = cos² (x/2) – sin² (x/2)
            = 1 – 2 sin² (x/2)
            = 2 cos²(x/2) – 1
• tan A = 2 tan (x/2) / [1 – tan²(x/2)]

Half-Angle Formula for Cos Derivation

We use cos2x = 2cos²x – 1 for finding the Half-Angle Formula for Cos

Put x = 2y in the above formula

cos (2)(y/2) = 2cos²(y/2) – 1

cos y = 2cos²(y/2) – 1

1 + cos y = 2cos²(y/2) 

2cos²(y/2) = 1 + cosy

cos²(y/2) = (1+ cosy)/2

cos(y/2) = ± √{(1+ cosy)/2}

Half-Angle Formula for Sin Derivation

We use cos 2x = 1 – 2sin²x for finding the Half-Angle Formula for Sin

Put x = 2y in the above formula

cos (2)(y/2) = 1 – 2sin²(y/2)     

cos y = 1 – 2sin²(y/2)   

2sin²(y/2) = 1 – cosy

sin²(y/2) = (1 – cosy)/2

sin(y/2) = ± √{(1 – cosy)/2}

Half-Angle Formula for Tan Derivation

We know that tan x  = sin x / cos x such that,

tan(x/2) = sin(x/2) / cos(x/2)

Putting the values of half angle for sin and cos. We get,

tan(x/2) = ± [(√(1 – cosy)/2 ) / (√(1+ cosy)/2 )]

tan(x/2) = ± [√(1 – cosy)/(1+ cosy) ]

Rationalising the denominator

tan(x/2) = ± (√(1 – cosy)(1 – cosy)/(1+ cosy)(1 – cosy))

tan(x/2) = ± (√(1 – cosy)²/(1 – cos²y))

tan(x/2) = ± [√{(1 – cosy)²/( sin²y)}]

tan(x/2) = (1 – cosy)/( siny)

Also, Check

• Real-Life Applications of Trigonometry
• Sin Cos Formulas

Solved Examples on Half Angle Formulas

Example 1: Determine the value of sin 15°

Solution:

We know that the formula for half angle of sine is given by:

sin x/2 = ± ((1 – cos x)/ 2) ^1/2

The value of sine 15° can be found by substituting x as 30° in the above formula

sin 30°/2 = ± ((1 – cos 30°)/ 2) ^1/2

sin 15° = ± ((1 – 0.866)/ 2) ^1/2

sin 15° = ± (0.134/ 2) ^1/2

sin 15° = ± (0.067) ^1/2

sin 15° = ± 0.2588

Example 2: Determine the value of sin 22.5°

Solution:

We know that the formula for half angle of sine is given by:

sin x/2 = ± ((1 – cos x)/ 2) ^1/2

The value of sine 15° can be found by substituting x as 45° in the above formula

sin 45°/2 = ± ((1 – cos 45°)/ 2) ^1/2

sin 22.5° = ± ((1 – 0.707)/ 2) ^1/2

sin 22.5° = ± (0.293/ 2) ^1/2

sin 22.5° = ± (0.146) ^1/2

sin 22.5° = ± 0.382

Example 3: Determine the value of tan 15°

Solution:

We know that the formula for half angle of sine is given by:

tan x/2 = ± (1 – cos x)/ sin x

The value of tan 15° can be found by substituting x as 30° in the above formula

tan 30°/2 = ± (1 – cos 30°)/ sin 30°

tan 15° = ± (1 – 0.866)/ sin 30

tan 15° = ± (0.134)/ 0.5

tan 15° = ± 0.268

Example 4: Determine the value of tan 22.5°

Solution:

We know that the formula for half angle of sine is given by:

tan x/2 = ± (1 – cos x)/ sin x

The value of tan 22.5° can be found by substituting x as 45° in the above formula

tan 30°/2 = ± (1 – cos 45°)/ sin 45°

tan 22.5° = ± (1 – 0.707)/ sin 45°

tan 22.5° = ± (0.293)/ 0.707

tan 22.5° = ± 0.414

Example 5: Determine the value of cos 15°

Solution:

We know that the formula for half angle of sine is given by:

cos x/2 = ± ((1 + cos x)/ 2) ^1/2

The value of sine 15° can be found by substituting x as 30° in the above formula

cos 30°/2 = ± ((1 + cos 30°)/ 2) ^1/2

cos 15° = ± ((1 + 0.866)/ 2) ^1/2

cos 15° = ± (1.866/ 2) ^1/2

cos 15° = ± (0.933) ^1/2

cos 15° = ± 0.965

Example 6: Determine the value of cos 22.5°

Solution:

We know that the formula for half angle of sine is given by:

cos x/2 = ± ((1 + cos x)/ 2) ^1/2

The value of sine 15° can be found by substituting x as 45° in the above formula

cos 45°/2 = ± ((1 + cos 45°)/ 2) ^1/2

cos 22.5° = ± ((1 + 0.707)/ 2) ^1/2

cos 22.5° = ± (1.707/ 2) ^1/2

cos 22.5° = ± ( 0.853 ) ^1/2

cos 22.5° = ± 0.923

FAQs on Half-Angle Formula

Question 1: What is the use of Half-Angle Formulas?

Answer:

Half-Angle formulas are used for finding trigonometric ratios of half of the standard angles such as 15°,22.5° and others. They are also used for solving complex trigonometric equations and are required in solving integrals, and differential equations.

Question 2: What is Half Angle Formula for Sin?

Answer:

Half-Angle formula for sin is 

sin A/2 = ±√[(1 – cos A) / 2]

Also, for any triangle with sides a, b, and c and semiperimeter be s, then

sin A/2 = √[(s – b) (s – c) / bc]

Question 3: What is Half Angle Formula for Cosine?

Answer:

Half-angle formula for cos is

cos A/2 = ±√[(1 + cos A)/2]

Also, for any triangle with sides a, b, and c and semiperimeter be s, then

cos (A/2) = √[ s (s – a)/bc]

Question 4: What is the formula for cos θ?

Answer:

For any right-angled triangle, with an angle θ the formula that is used to calculate the Cosine of the angle (θ) is 

Cos(θ) = adjacent / hypotenuse