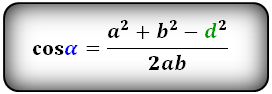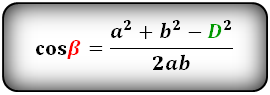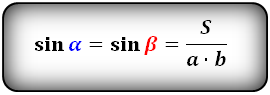maximandreev
+10
Решено
11 лет назад
Геометрия
5 – 9 классы
Площадь параллелограмма со сторонами 5 см и 8 см равна 32 см2. Найдите косинус наибольшего угла параллелограмма Решите пожалуйста)))
Смотреть ответ
1
Ответ
2
(9 оценок)
10
Santinello
11 лет назад
Светило науки – 25 ответов – 477 раз оказано помощи
Проведи к основанию высоту и вычисли её по формуле S=a*h(Площадь параллелограмма).Далее найди косинус острого угла, он будет равен 0,6.По формуле приведения(cos(180°-a),a-острый угол) косинус тупого угла(искомого)будет равен минус 0,6.
(9 оценок)
https://vashotvet.com/task/296544
Свойства углов параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
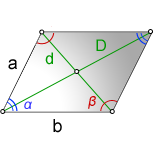
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и стороны:
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 05 ноября 2011
-
Обновлено: 13 августа 2021
several.wolf
Ученик
(234),
закрыт
7 лет назад
найдите косинус наибольшего угла параллелограмма
Naumenko
Высший разум
(856100)
10 лет назад
косинус тупого угла данного параллелограмма будет равен минус синусу острого.
чтобы найти синус острого угла. применим формулу площади параллелограмма как произведение длин 2-х соседних сторон на синус угла между ними.
откуда получается. что32= 5*8 *sina
дальнейший шаг очевиден. надеюсь.
Nikolay
Ученик
(119)
10 лет назад
Обозначим одну из сторон треугольника как x, тогда величина другой равна x+8 см.
Исходя из теоремы косинусов, получим:
282 = x2 + (x+8)2-2x(x+8)cos120o
784 = x2 + x2 +16x + 64 – 2x(x+8)(-0,5)
784 = 2×2+16x + 64 + x(x+8)
720 = 3×2 + 16x + 8x
3×2 + 24x +720 = 0
D=9216
x1=((-24)+96)/6=12 (второй корень является отрицательным числом и не имеет смысла в рамках решения задачи)
Таким образом, косинус угла P=12+(12+8)+28 = 60 см.
Ответ: 60 см
Здравствуйте, дорогие читатели. В этом выпуске разберемся, что нужно знать из 7 класса для легкого вычисления углов в параллелограмме и трапеции.
Как вы знаете, параллелограмм, прямоугольник, ромб и квадрат – это все параллелограммы. Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны.
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Значит для вычисления углов в параллелограмме и трапеции нам нужно вспомнить теоремы об углах, образованных при пересечении двух параллельных прямых секущей.
1) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусам.
Теперь применим это знание для решения задач из ОГЭ.
Задача №1
Для решения, воспользуемся свойством односторонних углов.
Для задания такого типа, можно мысленно продолжить стороны, у вас получится пересечение двух параллельных прямых секущей. Поэтому в данном случае воспользуемся тем, что сумма односторонних углов равна 180 градусов. Больший угол параллелограмма равен 180-61=119
Внимание!!! Будьте внимательны, в задании такого типа может быть написано, что нужно найти меньший угол. Меньший угол – это острый, больший угол – это тупой.
Точно также решается задача №2 с трапецией.
Меньший угол – это острый угол. Значит 180-131=49
Задача №3
Для решения такого типа задачи, нужно найти целый больший угол параллелограмма, он равен 70+35=105.
Найдем меньший угол параллелограмма – он острый, равен 180-105=75
2) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Для этой теоремы подходят следующие задачи:
Задача №4
Решение:
Угол 1 и угол 2 накрест лежащие, значит они раны. Так как АЕ биссектриса, то угол 2 равен углу 3. Значит угол А равен 33+33=66
Задача №5
Решение:
Так как трапеция равнобедренная, то углы при основаниях равны. Значит нам достаточно найти чему равен угол А, тогда мы найдем угол ADC.
Так как накрест лежащие углы при пересечении двух параллельных прямых секущей, равны, то угол А равен 50+30=80, значит угол ADC равен 80
В следующем выпуске, поговорим о том, как найти углы в параллелограмме, где используются другие свойства и теоремы, такие как свойство равнобедренного треугольника, сумма углов треугольника, свойство диагоналей ромба.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.