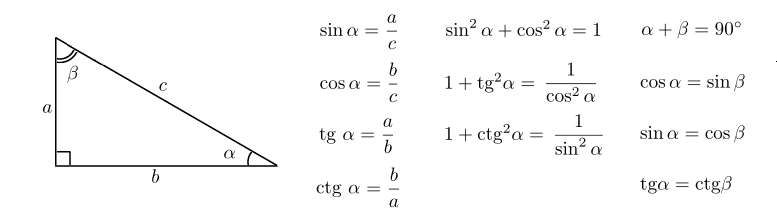Как найти косинус числа формула - Сайт, где вы сможете решить свои вопросы

Примеры:

(cos{⁡30^°}=)(frac{sqrt{3}}{2})
(cos⁡)(frac{π}{3})(=)(frac{1}{2})
(cos⁡2=-0,416…)

Содержание:

Аргумент и значение
Коcинус острого угла
Косинус числа
Косинус любого угла
Знаки по четвертям
Связь с другими функциями
Функция

Аргумент и значение

Косинус острого угла

Косинус острого угла можно определить с помощью прямоугольного треугольника – он равен отношению прилежащего катета к гипотенузе.

Пример:

1) Пусть дан угол и нужно определить косинус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить косинус.

Косинус острого угла больше (0) и меньше (1)

Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.

Косинус числа

Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: (frac{π}{2}), (frac{3π}{4}), (-2π).

Например, для числа (frac{π}{6}) – косинус будет равен (frac{sqrt{3}}{2}). А для числа (-)(frac{3π}{4}) он будет равен (-)(frac{sqrt{2}}{2}) (приблизительно (-0,71)).

Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.

Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.

Косинус любого угла

Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать – проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.

Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.

И, наконец, угол больше (360°) (угол КОС) – всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).

Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) – целых семь.

Стоит запомнить, что:

Косинус прямого угла равен нулю. Косинус тупого угла – отрицателен.

Знаки косинуса по четвертям

С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:

– там, где значения на оси от (0) до (1), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
– там, где значения на оси от (0) до (-1), косинус будет иметь знак минус (II и III четверти – фиолетовая область).

Пример. Определите знак (cos 1).
Решение: Найдем (1) на тригонометрическом круге. Будем отталкиваться от того, что (π=3,14). Значит единица, примерно, в три раза ближе к нулю (точке «старта»).

Если провести перпендикуляр к оси косинусов, то станет очевидно, что (cos⁡1) – положителен.
Ответ: плюс.

Связь с другими тригонометрическими функциями:

– синусом того же угла (или числа): основным тригонометрическим тождеством (sin^2⁡x+cos^2⁡x=1)
– тангенсом того же угла (или числа): формулой (1+tg^2⁡x=)(frac{1}{cos^2⁡x})
– котангенсом и синусом того же угла (или числа): формулой (ctgx=)(frac{cos{x}}{sin⁡x})
Другие наиболее часто применяемые формулы смотри здесь.

Функция (y=cos{x})

Если отложить по оси (x) углы в радианах, а по оси (y) – соответствующие этим углам значения косинуса, мы получим следующий график:

График данной функции называется косинусоида и обладает следующими свойствами:

– область определения – любое значение икса: (D(cos{⁡x} )=R)
– область значений – от (-1) до (1) включительно: (E(cos{x} )=[-1;1])
– четная: (cos⁡(-x)=cos{x})
– периодическая с периодом (2π): (cos⁡(x+2π)=cos{x})
– точки пересечения с осями координат:
ось абсцисс: (()(frac{π}{2})(+πn),(;0)), где (n ϵ Z)
ось ординат: ((0;1))
– промежутки знакопостоянства:
функция положительна на интервалах: ((-)(frac{π}{2})(+2πn;) (frac{π}{2})(+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: (()(frac{π}{2})(+2πn;)(frac{3π}{2})(+2πn)), где (n ϵ Z)
– промежутки возрастания и убывания:
функция возрастает на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
функция убывает на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
– максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=π+2πn), где (n ϵ Z).

Смотрите также:

Синус
Тангенс
Котангенс
Решение уравнения (cos⁡x=a)

Источник

Значения косинуса графически могут быть отображены в виде тригонометрической окружности, на которой угол α образует с осью прямоугольный треугольник. Из этого треугольника, спроецировав точку пересечения угла α с окружностью на ось синуса или косинуса, можно получить его приближенное значение.

Также тригонометрическая окружность показывает знак синуса и косинуса для каждого раскрытия угла α . Поскольку угол начинает раскрываться с правой стороны по оси косинусов, то значения косинуса угла α от 0° до 90° – положительны, так находятся правее нулевой точки отсчета. Угол α от 90° до 270° дает отрицательные значения косинусу, так как точка пересечения его с окружностью расположена левее оси синуса, то есть нуля. Косинус углов от 270° до 360° вновь становится положительным. Точные значения косинусов всех углов от 0° до 360° можно узнать из таблицы косинусов, приведенной ниже.

Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.

Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.

Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.

Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

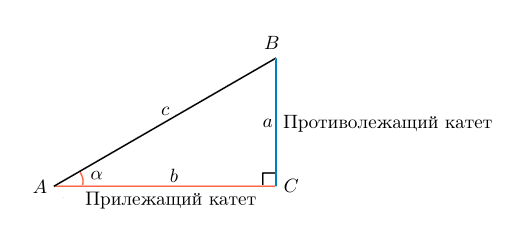
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).

Синус (sin) угла поворота

Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y

Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х

Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x

Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Синус и косинус определены для любых углов α .

Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )

Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )

При решении практических примеров не говорят “синус угла поворота α “. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности – точка A c координатами ( 1 , 0 ).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y

Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x

Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс – основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Коcинус – одна из тригонометрических функций. Значение косинуса определяется для угла или для числа (в этом случае используют числовую окружность).

Аргумент и значение

Косинус острого угла

Косинус острого угла можно определить с помощью прямоугольного треугольника – он равен отношению прилежащего катета к гипотенузе.

1) Пусть дан угол и нужно определить косинус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить косинус.

Косинус острого угла больше (0) и меньше (1)

Косинус числа

Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.

Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи : (frac<π><2>) , (frac<3π><4>) , (-2π).

Например, для числа (frac<π><6>) – косинус будет равен (frac<sqrt<3>><2>) . А для числа (-) (frac<3π><4>) он будет равен (-) (frac<sqrt<2>><2>) (приблизительно (-0,71)).

Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице .

Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.

Косинус любого угла

Стоит запомнить, что:

Косинус прямого угла равен нулю. Косинус тупого угла – отрицателен.

Знаки косинуса по четвертям

Если провести перпендикуляр к оси косинусов, то станет очевидно, что (cos⁡1) – положителен.
Ответ: плюс.

Связь с другими тригонометрическими функциями:

– синусом того же угла (или числа): основным тригонометрическим тождеством (sin^2⁡x+cos^2⁡x=1)
– тангенсом того же угла (или числа): формулой (1+tg^2⁡x=) (frac<1><cos^2⁡x>)
– котангенсом и синусом того же угла (или числа): формулой (ctgx=) (frac<cos><sin⁡x>)
Другие наиболее часто применяемые формулы смотри здесь .

Функция (y=cos)

График данной функции называется косинусоида и обладает следующими свойствами:

– область определения – любое значение икса: (D(cos <⁡x>)=R)
– область значений – от (-1) до (1) включительно: (E(cos )=[-1;1])
– четная: (cos⁡(-x)=cos)
– периодическая с периодом (2π): (cos⁡(x+2π)=cos)
– точки пересечения с осями координат:
ось абсцисс: (() (frac<π><2>) (+πn),(;0)), где (n ϵ Z)
ось ординат: ((0;1))
– промежутки знакопостоянства:
функция положительна на интервалах: ((-) (frac<π><2>) (+2πn;) (frac<π><2>) (+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: (() (frac<π><2>) (+2πn;) (frac<3π><2>) (+2πn)), где (n ϵ Z)
– промежутки возрастания и убывания:
функция возрастает на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
функция убывает на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
– максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=π+2πn), где (n ϵ Z).

Источник

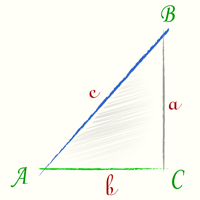
Косинус угла cos(A) — есть отношение прилежащего катета b к гипотенузе c

[ cos(A) = frac{b}{c} ]

Косинус угла — cos(A), таблица

0° Косинус угла 0 градусов	$ cos(0°) = cos(0) = 1 $	1.000
30° Косинус угла 30 градусов	$ cos(30°) = cosBig(Largefrac{pi}{6}normalsizeBig) = Largefrac{sqrt{3}}{2}normalsize $	0.866
45° Косинус угла 45 градусов	$ cos(45°) = cosBig(Largefrac{pi}{4}normalsizeBig) = Largefrac{sqrt{2}}{2}normalsize $	0.707
60° Косинус угла 60 градусов	$ cos(60°) = cosBig(Largefrac{pi}{3}normalsizeBig) = Largefrac{1}{2}normalsize $	0.500
90° Косинус угла 90 градусов	$ cos(90°) = cosBig(Largefrac{pi}{2}normalsizeBig) = 0 $	0.000

Вычислить, найти косинус угла cos(A) и угол, в прямоугольном треугольнике

Вычислить, найти косинус угла cos(A) по углу A в градусах

Вычислить, найти косинус угла cos(A) по углу A в радианах

Косинус угла — cos(A)	стр. 218

Источник

Определение косинуса угла

Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.

Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.

В случае с рисунком, описанным выше: cos⁡α=bccosalpha=frac{b}{c}

Задача 1

Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.

Решение

Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.

a2+b2=c2a^2+b^2=c^2

62+b2=1026^2+b^2=10^2

36+b2=10036+b^2=100

b2=64b^2=64

b=8b=8

Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:

cos⁡α=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8

Ответ

0.8

Задача 2

Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.

Решение

Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:

P=a+b+cP=a+b+c

25=9+4+c25=9+4+c

c=12c=12

При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:

cos⁡α=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82

Ответ

0.820.82

Решение задач по математике от экспертов сайта Студворк!

Тест по теме “Вычисление косинуса”

Источник

Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.

Синус, косинус, тангенс и котангенс. Определения

Зачем разделять понятия синуса, косинуса, тангенса и котангенса?

Определения тригонометрических функций

Что такое синус?

Синус угла (sin α) – это отношение противолежащего этому углу катета к гипотенузе.

Что такое косинус?

Косинус угла (cosα) – это отношение прилежащего катета к гипотенузе.

Что такое тангенс?

Тангенс угла (tg α) – это отношение противолежащего катета к прилежащему.

Котангенс угла (ctg α) – отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

Синус и косинус можно представить через экспоненту (экспоненциальная функция).

Приведем иллюстрацию.

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.

Что и почему важно и принято помнить в ходе такого нахождения?

Важно помнить!

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг – вся числовая прямая, то есть эти функции могут принимать любые значения.

Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором – теорему косинусов.

Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы.

Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).

Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.

Угол поворота

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.

Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).

Синус (sin или син) угла поворота

Синус угла поворота α – это ордината точки A1(x , y). sin α=y

Косинус (cos) угла поворота

Косинус угла поворота α – это абсцисса точки A1(x , y). cos α=икс

Тангенс (tg) угла поворота

Тангенс угла поворота α – это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx

Котангенс (ctg) угла поворота

Котанг угла поворота α – это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Важно помнить!

Простое правило: синус и косинус определены для любых углов α.

Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)

Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)

При решении практических примеров не говорят “синус угла поворота α”. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Например, синус числа 10π равен синусу угла поворота величиной 10π рад.

Начальная точка на окружности – точка A c координатами (1, 0).

Синус (sin) числа t

Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t=y

Косинус (cos) числа t

Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t=x

Тангенс (tg) числа t

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α, cos α, tg α, ctg α – это функции угла альфа, или функции углового аргумента.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс – основные тригонометрические функции.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.

sin α=A1HOA1=y1=y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Синус, косинус, тангенс и котангенс: основные формулы

Источник

Аргумент и значение

Косинус острого угла

Косинус острого угла можно определить с помощью прямоугольного треугольника – он равен отношению прилежащего катета к гипотенузе.

Косинус острого угла больше (0) и меньше (1)

Косинус числа

Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.

Косинус любого угла

Косинус прямого угла равен нулю. Косинус тупого угла – отрицателен.

Знаки косинуса по четвертям

Связь с другими тригонометрическими функциями:

Функция (y=cos{x})

Синус, косинус, тангенс и котангенс. Определения

Угол поворота

Числа

Тригонометрические функции углового и числового аргумента

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Коcинус – одна из тригонометрических функций. Значение косинуса определяется для угла или для числа (в этом случае используют числовую окружность).

Аргумент и значение

Косинус острого угла

Косинус острого угла можно определить с помощью прямоугольного треугольника – он равен отношению прилежащего катета к гипотенузе.

Косинус острого угла больше (0) и меньше (1)

Косинус числа

Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.

Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.

Косинус любого угла

Косинус прямого угла равен нулю. Косинус тупого угла – отрицателен.

Знаки косинуса по четвертям

Связь с другими тригонометрическими функциями:

Функция (y=cos)

Косинус угла — cos(A), таблица

Вычислить, найти косинус угла cos(A) и угол, в прямоугольном треугольнике

Вычислить, найти косинус угла cos(A) по углу A в градусах

Вычислить, найти косинус угла cos(A) по углу A в радианах

Косинус угла — cos(A)

Тест по теме “Вычисление косинуса”

Синус, косинус, тангенс и котангенс. Определения

Угол поворота

Числа

Тригонометрические функции углового и числового аргумента

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Синус, косинус, тангенс и котангенс: основные формулы

Вам также может понравиться

Как найти мощность тока при параллельном соединении

Как найди хорошего парикмахера

Как найти в контакте по email

Добавить комментарий Отменить ответ