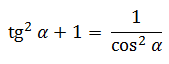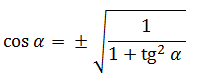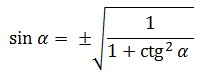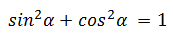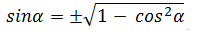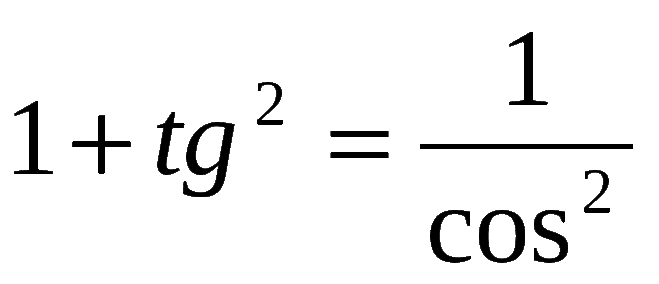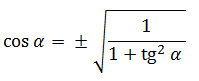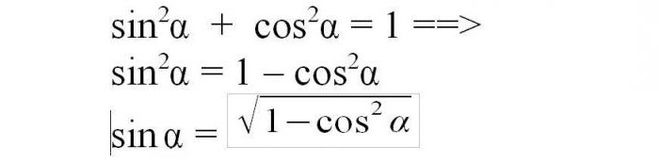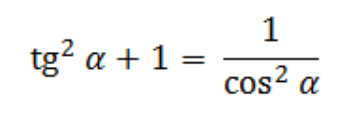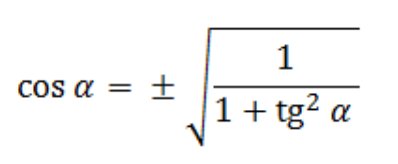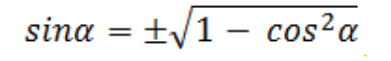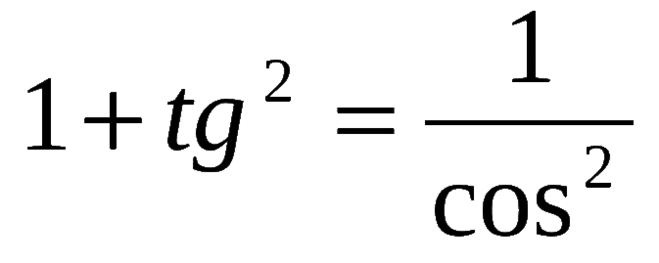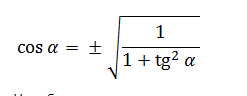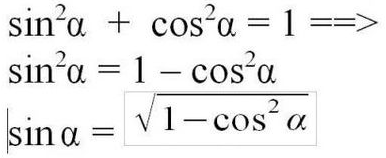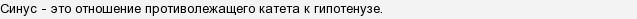Как найти косинус если знает только тангенс

Как найти синус, если известен тангенс? Как найти косинус, если известен тангенс? довольно часто при решении уравнений и упрощении тригонометрических выражений требуется найти синус или косинус через тангенс. Для этого существуют специальные формулы. Итак, для нахождения косинуса нужно извлечь квадратный корень из дроби в числителе которой единица, а в знаменателе выражение единица плюс тангенс в квадрате. А вот для того, чтобы найти синус нужно извлечь квадратный корень из выражения один минус дробь в числителе которой единица, а в знаменателе выражение единица плюс тангенс в квадрате. Но нужно обратить на знак синуса и косинуса, в зависимости от того в какой четверти находится угол. И если синус находим, то в 3 и 4 четвертях он будет отрицателен, а если косинус, то во второй и третьей. система выбрала этот ответ лучшим Ксарф­акс [156K] 4 года назад  Косинус через тангенс Для того, чтобы найти значение косинуса по известному тангенсу, нужно воспользоваться одним из тригонометрических тождеств. Сумма квадрата тангенса и единицы равна отношению единицы и квадрата косинуса. Отсюда можно выразить косинус: Наличие знака ± связано с тем, что в одних четвертях косинус угла может быть положительным, а в других – отрицательным. То есть в условии задачи должна оговариваться четверть, в которой находится угол. ** Пример. tgα = 1/√3, α находится в 1 четверти (0 < α < 90). Найдём косинус: cosα = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2. Итак, если тангенс равен 1/√3, то косинус равен √3/2. Нетрудно догадаться, что мы имели дело с углом 30°. Синус через тангенс Здесь также понадобятся тригонометрические тождества. Можно пойти двумя путями: 1) Выразить котангенс через тангенс и найти синус по котангенсу. 2) Найти косинус по тангенсу, а затем воспользоваться основным тригонометрическим тождеством. ** Пример. tgα = √3, α находится в 1 четверти (0 < α < 90). Найдём котангенс: ctga = 1 / tgα = 1 / √3. Теперь найдём синус: sina = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2. Или: cosa = √ ( 1 / (1 + 3)) = √ (1/4) = 1/2. sina = √ (1 – 1/4) = √ (3/4) = √3/2. Таким образом, если тангенс равен √3, то синус равен √3/2. Здесь также понятно, что это угол 60°. Серге­йНико­лаев [127K] 5 месяцев назад  Для этого существуют вполне определённые математические тригонометрические формулы. Например, косинус любого угла можно найти, зная его тангенс, исходя из соотношения что он равен корню квадратному из дроби, в числителе которой будет единица, а в знаменателе квадрат тангенса плюс единица. Только надо учитывать момент, что он может быть положительным и отрицательным. Зная косинус, несложно вычислить и синус любого угла, если вспомнить, что сумма их квадратов всегда равна единице. Также можно найти котангенс этого угла, разделив 1 на тангенс, а дальше воспользоваться аналогичной приведённой в первом абзаце формулой для синуса и котангенса. Optor­ius [13.8K] 6 месяцев назад  Синус и косинус через тангенс можно найти: 1 – По таблице значений тригонометрических функций некоторых углов. 2 – Через вычисления по формулам тригонометрических тождеств. Сначала находим косинус, затем по нему синус. 3 – Через универсальные тригонометрические подстановки (полуугловые подстановки). Такой способ обычно используют при вычислении интегралов, он дает приближенный результат. Для примера: Возьмем tg = √3. По таблице sin = √3/2 ≈ 0,866. По второму способу sin = √(1-1/4) ≈ 0,866. По третьему способу sin = √3/(7/4) ≈ 0,9897. Дмитр­ий Подко­паев [95] 2 года назад  Приведу на всякий случай, на мой взгляд, наиболее общий способ нахождения синуса и косинуса по тангенсу. Как говорится определил знак подставил в выражение и получил ответ. В алгебре и геометрии очень часто при решении задач используются тригонометрические формулы, которые чаще называют тригонометрическими тождествами. Из любого тригонометрического тождества несложно вывести новую формулу, необходимую для нахождения одной из величин, входящих в его состав. ****************­*****************­*****************­*****************­***** Для того, чтобы найти косинус угла, зная его тангенс, возьмем тригонометрическое тождество: . Из данного тождества выводим новую формулу для вычисления косинуса: Не забываем, что косинус может принимать как положительные, так и отрицательные значения в зависимости от четверти нахождения угла. ****************­*****************­*****************­*****************­***** Для вычисления синуса угла через его тангенс можно действовать по-разному. Например, вычислить по выведенной выше формуле косинус угла, а затем воспользоваться еще одним тригонометрическим тождеством и вывести из него формулу для вычисления синуса угла: Алиса в Стран­е [363K] 3 года назад  В тригонометрических тождествах нет, конечно, ничего сложного, вот только запомнить их все так, чтобы не пользоваться справочными материалами, обычному человеку достаточно трудно, поэтому всегда приходится где-то искать эти формулы. Вот одна из них: Из нее то мы и будем получать формулу для выполнения задания из вопроса, а именно – нахождения косинуса через тангенс, проведя несложные преобразования, получим: Как видите, действительно все очень просто. Теперь, найдя косинус, воспользуемся основным тригонометрическим тождеством, преобразуем его, чтобы найти синус через уже найденный косинус, формула такая: RIOLI­t [176K] 5 лет назад  конечно тангенс угла- это отношение синуса этого угла к косинусу того же угла- условно- а/б= с и а= с*в, в= а/с, сразу видно, что, кроме с, что- нибудь еще должно быть дано иначе не расколоть задачку, разве с будет равно 1 или еще какому замечательному значению, позволяющему определить величину угла угла. Krust­all [125K] 8 месяцев назад  Синус, косинус и тангенс являются тригонометрическими функциями. Исторически они возникли как отношения между сторонами прямоугольного треугольника, поэтому их удобнее вычислять через прямоугольный треугольник. Однако через него могут быть выражены только тригонометрические функции острых углов. Для тупых углов вам нужно будет вставить окружность. Иногда, необходимо найти синус или косинус через тангенс. Для этого существуют специальные формулы. Итак, чтобы найти косинус, нужно извлечь квадратный корень из дроби, в числителе которой единица, а в знаменателе выражение единица плюс тангенс к квадрату. Но чтобы найти синус, нужно извлечь квадратный корень из выражения один минус дробь в числителе которого единица, а в знаменателе выражение равно единице плюс касательная к квадрату. Но нужно обращать внимание на знак синуса и косинуса в зависимости от того, в какой четверти находится угол. И если мы найдем синус, то в 3-й и 4-й четвертях он будет отрицательным, а если косинус – во 2 и 3. Если говорить о тангенсе угла, то является отношением синуса по отношению к косинусу. Так, следует воспользоваться тригонометрическим тождеством. Согласно ему выводится формула, которую используем для того, чтобы вычислить косинус. Вы можете вычислить по формуле, а также воспользуюсь еще 1 тригонометрическим тождеством, выведя формула вычислить: Лара Изюми­нка [59.8K] 2 года назад  Итак , чтобы найти синус нужно взять корень из выражения 1 деленное на 1 плюс тангенс в квадрате. Далее по основному тригонометрическому тождесьву можно найти косинус. Для этого нужно извлечь квадратный корень их 1 минус только что найденнный синус в квадрате. sin=sqrt(1/(1+((1/tg)**2))) cos=sqrt(1/(1+((1/ctg)**2))) Знаете ответ?

Смотрите также: Что такое тангенс, катангенс, синус, косинус, секанс, касеканс? Как найти тангенс, если известен косинус и синус? Как выучить значения косинусов, синусов, тангенсов? Какова этимология слов “тангенс, котангенс, синус, косинус, тон”? А вам в жизни когда нибудь приходились столкнуться с косинусами, синусами? Как легко запомнить тригонометрический круг (единичную окружность)? Как узнать синус угла в треугольнике если известны синусы остальных углов? Определите знак выражения и как вы нашли? Sin имеет много рациональных значений, а в таблицах мало, почему (см.)? Для чего и где нужны математические Sin и Cos?

Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.

Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).

Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.

Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника

Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co

Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.

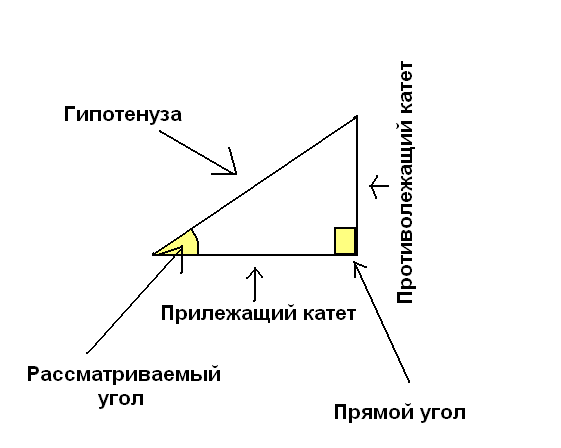
Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.

Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.

Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.

Итак,

Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.

Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.

Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.

Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.

Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.

Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.

Как найти углы в прямоугольном треугольнике, если известны стороны?

Дан треугольник АВС, угол С — прямой.

Стороны АВ, АС и ВС известны.

Т.к. угол С — прямой, он равен 90 градусам.

Другие углы можно найти, например, так:

если известен катет и гипотенуза

sinA = BC / AB,

sinB = AC / AB,

если известны два катета

tg A = BC / AC

tg B = AC / BC

Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.

Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.

Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.

sin 15° = 0,259

arcsin0,259 = 15°

Как найти углы в прямоугольном треугольнике, если известен один угол?

Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.

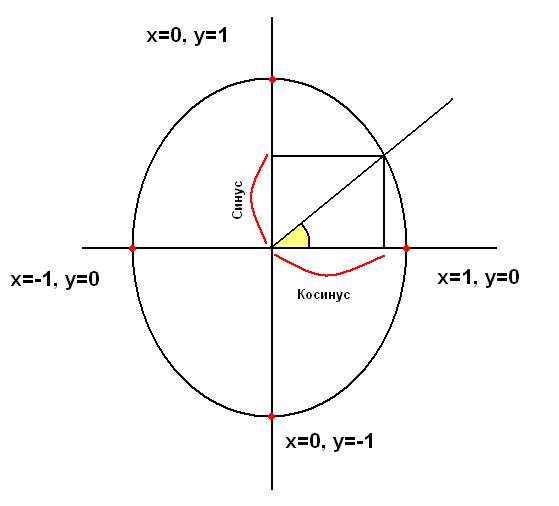
Еединичная окружность (единичный круг)

Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).

Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).

Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.

Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).

Координатные четверти отсчитываются так:

                        y

                       |

                       |

(II четверть)   |   (I четверть)

                       |

________________________ x

                       |0

                       |

(III четверть)  |   (IV четверть)

                       |

                       |

Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).

Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).

Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).

Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).

Например:

• углы первой четверти: 30 градусов, 85 градусов, пи/4;
• углы второй четверти: 120 градусов, 178 градусов;
• углы третьей четверти: 205 градусов, 260 градусов;
• углы четвертой четверти: 272 градуса, 305 градусов.

Тригонометрические функции

К тригонометрическим функциям относятся функции:

y = sin x;

y = cos x;

y = tg x;

y = ctg x;

y = sec x;

y = cosec x.

Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.

Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.

Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.

Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.

Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.

Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.

Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.

Как найти синус угла, если известен косинус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

sin²a = 1 − cos²a

|sin a| = КОРЕНЬ(1 − cos²a)

sin a = ± КОРЕНЬ(1 − cos²a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)

Как найти косинус угла, если известен синус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

cos²a = 1 − sin²a

|cos a| = КОРЕНЬ(1 − sin²a)

cos a = ± КОРЕНЬ(1 − sin²a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)

Как найти синус угла, если известен котангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + ctg² a = 1/sin² a

sin² a = 1 / (1 + ctg² a)

|sin a| = 1/ КОРЕНЬ(1 + ctg² a)

sin a = ±1/ КОРЕНЬ(1 + ctg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)

Как найти косинус угла, если известен тангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + tg² a = 1/cos² a

cos² a = 1 / (1 + tg² a)

|cos a| = 1/ КОРЕНЬ(1 + tg² a)

cos a = ±1/ КОРЕНЬ(1 + tg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)

Тригонометрическое тождество

Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.

Основные тригонометрические тождества:

sin²a + cos²a = 1

tg a = sin a / cos a

ctg a = cos a / sin a

sec a = 1 / cos a

cosec a = 1 / sin a

Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)

• arcsin — читается: арксинус;
• arcos — читается: арккосинус;
• arctg — читается: арктангенс;
• arcctg — читается: арккотангенс.

arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.

Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:

y = arcsin x sin y = x

Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:

y = arccos x cos y = x

Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:

y = arctg x tg y = x

Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:

y = arctg x tg y = x

Например,

sin 30° = 0,5

arcsin0,5 = 30°

Синусоида и косинусоида

График функции y = sin x называется синусоидой.

График функции y = cos x называется косинусоидой.

Источники информации:

• Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
• В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
• docme.ru — зачем нужна тригонометрия?
• ru.wikipedia.org — Википедия — тригонометрия;
• ru.wikihow.com — как изучать тригонометрию?

6 ответов:

Читайте также

Автор	Сообщение
	Заголовок сообщения: Зная тангенс, найти косинус Добавлено: 13 янв 2013, 11:35
Одарённый Зарегистрирован: 10 янв 2012, 21:35 Сообщений: 141 Cпасибо сказано: 36 Спасибо получено: 1 раз в 1 сообщении Очков репутации: -1	объясните,как это получилось?! оч надо Вложения: hw.jpg [ 5.31 Кб | Просмотров: 34255 ]
Вернуться к началу

Yurik	Заголовок сообщения: Re: Из tg в cos Добавлено: 13 янв 2013, 12:03
	[math]begin{gathered} tgalpha = frac{{sin alpha }}{{cos alpha }} = frac{{sqrt {1 – {{cos }^2}alpha } }}{{cos alpha }} = sqrt {frac{1}{{{{cos }^2}alpha }} – 1} = frac{3}{4},,, = > ,,,frac{1}{{{{cos }^2}alpha }} = frac{{25}}{{16}} hfill \ {cos ^2}alpha = frac{{16}}{{25}},,, = > ,,cos alpha = pm frac{4}{5} hfill \ end{gathered}[/math] Но гораздо проще представить себе тригонометрический круг, и всё станет понятным. Последний раз редактировалось Yurik 13 янв 2013, 12:19, всего редактировалось 1 раз.
Вернуться к началу
	За это сообщение пользователю Yurik “Спасибо” сказали: jackystorm

jackystorm	Заголовок сообщения: Re: Из tg в cos Добавлено: 13 янв 2013, 12:13
	Yurik писал(а): [math]begin{gathered} tgalpha = frac{{sin alpha }}{{cos alpha }} = frac{{sqrt {1 – {{cos }^2}alpha } }}{{cos alpha }} = sqrt {frac{1}{{{{cos }^2}alpha }} – 1} = frac{3}{4},,, = > ,,,frac{1}{{{{cos }^2}alpha }} = frac{{25}}{{16}} hfill \ {cos ^2}alpha = frac{{16}}{{25}},,, = > ,,cos alpha = pm frac{4}{5} hfill \ end{gathered}[/math] спасибо
Вернуться к началу

jackystorm	Заголовок сообщения: Re: Из tg в cos Добавлено: 13 янв 2013, 12:33
	Yurik писал(а): [math]begin{gathered} tgalpha = frac{{sin alpha }}{{cos alpha }} = frac{{sqrt {1 – {{cos }^2}alpha } }}{{cos alpha }} = sqrt {frac{1}{{{{cos }^2}alpha }} – 1} = frac{3}{4},,, = > ,,,frac{1}{{{{cos }^2}alpha }} = frac{{25}}{{16}} hfill \ {cos ^2}alpha = frac{{16}}{{25}},,, = > ,,cos alpha = pm frac{4}{5} hfill \ end{gathered}[/math] Но гораздо проще представить себе тригонометрический круг, и всё станет понятным. а можете объяснить,как тут (в показанном примере) из тех формул “формулы преобразования координат запишутся в виде: “ получается “Подставляем выражения “старых” координат через “новые” в исходное уравнение кривой и, проделав достаточно громоздкие, но простые преобразования, получаем: “ я пробовала подставлять,но у меня не сходится с тем,как у них
Вернуться к началу

jackystorm	Заголовок сообщения: Re: Из tg в cos Добавлено: 13 янв 2013, 13:01
Вернуться к началу

Формулы связи тригонометрических функций. Примеры из ЕГЭ

Внимание! Эти формулы работают только если аргументы у тригонометрических функций одинаковые, т.е.

(sin^2⁡ 776^° +cos^2⁡ 776^° =1)
(tg, 3xcdot ctg, 3x=1)

(sin^2⁡x+cos^2⁡3x≠1)
(tg, xcdot ctg, y≠1)

Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.

Примеры применения формул связи

Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения , заменяя одну функцию другой и так далее.

Пример. Найдите (5sin⁡,α), если (cos,⁡α=frac>) и (α∈(frac;2π)).
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:

Подставим вместо косинуса его значение:

Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида (x^2=a) (при (a>0)) два корня (x_1=sqrt) и (x_2=-sqrt). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»

Вернемся к задаче. Получилось, что синус может иметь значение (frac) , а может (-) (frac) . И какое значение нам надо выбрать — с минусом или плюсом? Тут нам на помощь приходит информация, что (α∈(frac;2π)). Давайте нарисуем числовую окружность и отметим отрезок ((frac;2π)).

Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).

Значит, в нашем случае (sin,⁡α=-frac) т.е. (5sin,⁡α=5cdot(-frac)=-1).

Пример.Найдите (tg,α), если (cos,⁡α=) (frac>) и (α∈(frac;2π)).
Решение. Есть 2 пути решения этой задачи:

— напрямую вычислить тангенс через формулу (tg^2α+1=) (frac) ;
— сначала с помощью тождества (sin^2⁡α+cos^2⁡α=1) найти (sin⁡,α), а потом через формулу (tg,α=) (frac) получить тангенс.

В учебниках обычно идут первым путем, поэтому мы пойдем вторым.

Пример. Известно, что (tg,α=-frac) и (frac<α<π). Найдите значения трех других тригонометрических функций угла (α).
Решение. Проще всего из тангенса найти котангенс:

Теперь вычислим косинус по упомянутой выше формуле:

Опять перед нами стоит выбор плюс или минус. Отметим отрезок ((frac;π)) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.

Очевидно, что косинус отрицателен в этой четверти, а значит (cos,⁡α=-) (frac) .

Осталось найти синус:

Опять используем круг, чтобы определить знак.

Пример (ЕГЭ). Найдите (tg^2 α), если (5 sin^2⁡α+13 cos^2⁡α=6).
Решение. Давайте пойдем от того, что известно. В равенстве (5 sin^2⁡α+13 cos^2⁡α=6) синус заменим на косинус:

Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения (tg^2α) хорошо подходит формула (tg^2α+1=) (frac) :

Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.

Пример. Упростите выражение (frac) (-ctg^2 α-cos^2 β).
Решение.

Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу.

Здравствуйте!
Помогите разобраться как найти cos, tg и ctg, если известен только sin.
Спасибо!

Разберемся, как найти cos, tg и ctg, если известен только sin.
Начнем с косинуса.
Синус и косинус связывает много тригонометрических тождеств, но наиболее часто используется и является зачастую самым удобным основное тригонометрическое тождество. С его помощью можно найти квадрат косинуса или сам косинус. Приведем вариант тождества для вычисления косинуса через синус:

Так можно найти квадрат косинуса:

Так можно найти косинус:

Рассмотрим тангенс.
Поскольку тангенс можно найти через отношение синуса на косинус, а косинус можно выразить через синус, то получим следующую формулу:

с котангенсом ситуация похожа на тангенс, только котангенс равен отношению косинуса к синусу, поскольку котангенс является обратной функцией к тангенсу. Получим соответственно обратную формулу и для его нахождения по сравнению с тангенсом:

Есть, конечно же, и другие формулы для вычисления значений заданных функций через синус, но представленные выше являются основными, тем более их можно не заучивать наизусть, а при необходимости вывести самостоятельно. Как видите, для этого достаточно знать только одну формулу и основное свойство функций тангенс и котангенс.

Как найти синус и косинус через тангенс?

Для того, чтобы найти значение косинуса по известному тангенсу, нужно воспользоваться одним из тригонометрических тождеств.

Сумма квадрата тангенса и единицы равна отношению единицы и квадрата косинуса.

Отсюда можно выразить косинус:

Наличие знака ± связано с тем, что в одних четвертях косинус угла может быть положительным, а в других — отрицательным.

То есть в условии задачи должна оговариваться четверть, в которой находится угол.

tgα = 1/√3, α находится в 1 четверти (0 < α < 90).

Найдём косинус: cosα = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2.

Итак, если тангенс равен 1/√3, то косинус равен √3/2.

Нетрудно догадаться, что мы имели дело с углом 30°.

Синус через тангенс

Здесь также понадобятся тригонометрические тождества.

Можно пойти двумя путями:

1) Выразить котангенс через тангенс и найти синус по котангенсу.

2) Найти косинус по тангенсу, а затем воспользоваться основным тригонометрическим тождеством.

tgα = √3, α находится в 1 четверти (0 < α < 90).

Найдём котангенс: ctga = 1 / tgα = 1 / √3.

Теперь найдём синус: sina = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2.

cosa = √ ( 1 / (1 + 3)) = √ (1/4) = 1/2.

sina = √ (1 — 1/4) = √ (3/4) = √3/2.

Таким образом, если тангенс равен √3, то синус равен √3/2.

Здесь также понятно, что это угол 60°.

В алгебре и геометрии очень часто при решении задач используются тригонометрические формулы, которые чаще называют тригонометрическими тождествами. Из любого тригонометрического тождества несложно вывести новую формулу, необходимую для нахождения одной из величин, входящих в его состав.

Для того, чтобы найти косинус угла, зная его тангенс, возьмем тригонометрическое тождество:

Из данного тождества выводим новую формулу для вычисления косинуса:

Не забываем, что косинус может принимать как положительные, так и отрицательные значения в зависимости от четверти нахождения угла.

Для вычисления синуса угла через его тангенс можно действовать по-разному.

Например, вычислить по выведенной выше формуле косинус угла, а затем воспользоваться еще одним тригонометрическим тождеством и вывести из него формулу для вычисления синуса угла:

довольно часто при решении уравнений и упрощении тригонометрических выражений требуется найти синус или косинус через тангенс.

Для этого существуют специальные формулы. Итак, для нахождения косинуса нужно извлечь квадратный корень из дроби в числителе которой единица, а в знаменателе выражение единица плюс тангенс в квадрате.

А вот для того, чтобы найти синус нужно извлечь квадратный корень из выражения один минус дробь

в числителе которой единица, а в знаменателе выражение единица плюс тангенс в квадрате.

Но нужно обратить на знак синуса и косинуса, в зависимости от того в какой четверти находится угол. И если синус находим, то в 3 и 4 четвертях он будет отрицателен, а если косинус, то во второй и третьей.