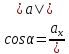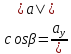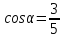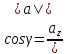Для удобства сразу же приведем таблицу с всеми тригонометрическими тождествами. Всегда удобно открыть формулы в одном месте, выбрать нужную и решить пример. После таблицы мы по отдельности рассмотрим каждую тригонометрическую формулу: обсудим ее вывод и порешаем примеры.
- Основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$ - Определение тангенса и котангенса через синус и косинус:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$ - Cвязь тангенса и котангенса:
$$tg(alpha)=frac{1}{ctg(alpha)};$$
$$tg(alpha)*ctg(alpha)=1;$$ - Тангенс через косинус. Котангенс через синус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$ctg(alpha)^2+1=frac{1}{sin(alpha)^2};$$ - Синус суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$ - Косинус суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$ - Тангенс суммы и разности:
$$tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};$$
$$tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};$$ - Котангенс суммы и разности:
$$сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};$$
$$сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};$$ - Двойной угол:
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$ - Тройной угол:
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$ - Формулы половинного угла:
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$ - Понижение степени:
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$ - Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$ - Преобразование произведения тригонометрических функций:
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$ - Формулы подстановки тангенса:
$$sin(alpha)=frac{2*tg(frac{alpha}{2})}{1+tg(frac{alpha}{2})^2};$$
$$cos(alpha)=frac{1-tg(frac{alpha}{2})^2}{1+tg(frac{alpha}{2})^2};$$
$$tg(alpha)=frac{2*tg(frac{alpha}{2})}{1-tg(frac{alpha}{2})^2};$$
$$ctg(alpha)=frac{1-tg(frac{alpha}{2})^2}{2*tg(frac{alpha}{2})};$$ - Формулы приведения можно найти в отдельной статье
Зачем нужны тригонометрические формулы?
Как видите, тригонометрических формул очень много. Тут еще и не все приведены. Но на ваше счастье, учить всю эту таблицу не нужно. Достаточно знать только основные: №1-6, 9. Остальные на ЕГЭ по профильной математике встречаются крайне редко, а если и попадутся, то, скорее всего, будут даны в справочных материалах.
Но для участия в олимпиадах или, если вы хотите поступать в сильный математический ВУЗ через вступительные экзамены, то вам может понадобиться вся таблица. По крайней мере, у вас точно должно быть представление о существовании таких формул, чтобы их вывести в случае необходимости. Да, большинство из них легко выводятся.
Тригонометрические формулы нужны, чтобы связать все тригонометрические функции между собой. Если вы знаете одну из функций, например, синус, то, используя эти формулы, можно легко найти оставшиеся три тригонометрические функции (косинус, тангенс и котангенс). Кроме этого тождества позволяют упростить выражение под тригонометрической функцией: например, выразить синус от двойного угла через комбинацию тригонометрических функций от одинарного угла, что бывает очень полезно при решении тригонометрических уравнений и неравенств.
Обсудим и порешаем примеры на все формулы из таблицы.
Основное тригонометрическое тождество
$$mathbf{sin(alpha)^2+cos(alpha)^2=1;}$$
Эту формулу можно считать главной и самой часто используемой в тригонометрии. Она выводится при помощи определения синуса и косинуса через прямоугольный треугольник и теоремы Пифагора. Не буду еще раз описывать вывод, с ним можно познакомиться в самой первой главе по тригонометрии.
При помощи основного тригонометрического тождества очень удобно искать значение синуса, если известен косинус и наоборот. Разберем пример:
Пример 1
Найдите (3sqrt{2}*sin(alpha)=?), если (cos(alpha)=frac{1}{3}) и (alphain(0;frac{pi}{2})). (ЕГЭ)
Чтобы найти значение выражения (3sqrt{2}*sin(alpha)) необходимо сначала найти значение синуса.
Формула, которая связывает и синус, и косинус – это основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$
Просто подставим в нее известное значение косинуса
$$sin(alpha)^2+left(frac{1}{3}right)^2=1;$$
$$sin(alpha)^2+frac{1}{9}=1;$$
$$sin(alpha)^2=1-frac{1}{9};$$
$$sin(alpha)^2=frac{8}{9};$$
$$sin(alpha)=pmsqrt{frac{8}{9}}=pmfrac{2sqrt{2}}{3};$$
Обратите внимание на знак (pm), отрицательное значение синуса нас тоже устраивает, так как при подстановке и возведении в квадрат знак минус исчезает.
В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?
В этом нам поможет дополнительное условие на (alphain(0;frac{pi}{2})), что соответсвует первой четверти на тригонометрической окружности. Раз (alpha) лежит в первой четверти, то синус должен быть положительный. Выбираем положительное значение синуса:
$$sin(alpha)=frac{2sqrt{2}}{3};$$
И подставим найденное значение в искомое выражение:
$$3sqrt{2}*sin(alpha)=3sqrt{2}*frac{2sqrt{2}}{3}=4.$$
Ответ: (4.)
Аналогично по основному тригонометрическому тождеству можно находить значение косинуса, если известен синус.
Основные тригонометрическое тождество это ключ к решению более половины всех тригонометрических уравнений.
Основные связи тригонометрических функций
А как найти тангенс или котангенс, если нам, например, известен косинус? Посмотрите на формулы №2, для того, чтобы найти тангенс, нужно знать и косинус, и синус:
$$mathbf{tg(alpha)=frac{sin(alpha)}{cos(alpha)};}$$
$$mathbf{ctg(alpha)=frac{cos(alpha)}{sin(alpha)};}$$
Но зная косинус, мы легко можем найти синус по основному тригонометрическому тождеству, а потом уже найти тангенс.
Пример 2
Найдите (tg(alpha)) и (ctg(alpha)), если (cos(alpha)=frac{sqrt{10}}{10}) и (alpha in (frac{3pi}{2};2pi)).
Сначала находим значение синуса:
$$sin(alpha)^2+cos(alpha)^2=1;$$
$$sin(alpha)^2+left(frac{sqrt{10}}{10}right)^2=1;$$
$$sin(alpha)^2+frac{1}{10}=1;$$
$$sin(alpha)^2=1-frac{1}{10};$$
$$sin(alpha)^2=frac{9}{10};$$
$$sin(alpha)=pmsqrt{frac{9}{10}}=pmfrac{3}{sqrt{10}};$$
Так как по условию задачи (alpha in (frac{3pi}{2};2pi)), что соответсвует четвертой четверти на тригонометрической окружности, то (sin(alpha)<0). Выбираем отрицательное значение:
$$sin(alpha)=-frac{3}{sqrt{10}};$$
Теперь нам известны значения и косинуса, и синуса, можем найти тангенс:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)}=frac{-frac{3}{sqrt{10}}}{frac{sqrt{10}}{10}}=-frac{3}{sqrt{10}}*frac{10}{sqrt{10}}=-3;$$
Котангенс можно найти аналогично по формуле:
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
Но поступим проще и воспользуемся тригонометрической формулой, связывающей тангенс с котангенсом:
$$mathbf{сtg(alpha)=frac{1}{tg(alpha)};}$$
$$сtg(alpha)=frac{1}{-3}=-frac{1}{3};$$
Ответ: (tg(alpha)=-3;) (ctg(alpha)=-frac{1}{3}.)
Как видите, чтобы найти тангенс или котангенс через косинус или синус, необходимо воспользоваться сразу двумя тригонометрическими формулами. Это не очень удобно, поэтому очень полезны тригонометрические формулы, связывающие тангенс с косинусом или котангенс с синусом напрямую:
$$mathbf{tg(alpha)^2+1=frac{1}{cos(alpha)^2};}$$
$$mathbf{ctg(alpha)^2+1=frac{1}{sin(alpha)^2};}$$
Вывод связи тангенса с косинусом и котангенса с синусом
Полезно знать, как они выводятся. Вывод, на самом деле, элементарный, с использованием основного тригонометрического тождества и определения тангенса через синус и косинус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$left(frac{sin(alpha)}{cos(alpha)}right)^2+1=frac{1}{cos(alpha)^2};$$
Приводим левую часть к общему знаменателю:
$$frac{sin(alpha)^2}{cos(alpha)^2}+frac{cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
$$frac{sin(alpha)^2+cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
В числителе у нас получилось основное тригонометрическое тождество:
$$frac{1}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
Получилось верное равенство – формула доказана. Аналогично доказывается формула для котангенса и синуса. (В качестве упражнения докажите ее сами).
Если решать пример №2 по этим формулам, то решение заметно сокращается:
$$tg(alpha)^2+1=frac{1}{left(frac{sqrt{10}}{10}right)^2};$$
$$tg(alpha)^2+1=10;$$
$$tg(alpha)^2=9;$$
$$tg(alpha)=pm3;$$
Так как (alpha in (frac{3pi}{2};2pi)), то тангенс будет отрицательным:
$$tg(alpha)=-3;$$
Формулы суммы и разности тригонометрических функций
- Синус суммы и разности:
$$mathbf{sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);}$$
$$mathbf{sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);}$$ - Косинус суммы и разности:
$$mathbf{cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);}$$
$$mathbf{cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);}$$ - Тангенс суммы и разности:
$$mathbf{tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};}$$
$$mathbf{tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};}$$ - Котангенс суммы и разности:
$$mathbf{сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};}$$
$$mathbf{сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};}$$
Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.
Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:
Пример 3
Упростить выражение (sin(frac{pi}{2}+alpha)).
Воспользуемся формулой синуса суммы:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(frac{pi}{2}+alpha)=sin(frac{pi}{2})*cos(alpha)+sin(alpha)*cos(frac{pi}{2})=$$
$$=1*cos(alpha)+sin(alpha)*0=cos(alpha);$$
Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:
Пример 4
Найдите значение (sin(15^o)=?)
(15^o) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим (15^o) в виде разности стандартных углов (15^o=45^o-30^o). И воспользуемся формулой синуса разности:
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(15^o)=sin(45^o-30^o)=sin(45^o)*cos(30^o)-sin(30^o)*cos(45^o)=$$
$$=frac{sqrt{2}}{2}*frac{sqrt{3}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
Вот мы наши синус (15^o). Получилось такое иррациональное некрасивое выражение, так и оставляем.
Ответ: (sin(15^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Пример 5
Найдите значение (cos(75^o)=?)
(75^o) можно представить в виде суммы стандартных углов (75^o=30^o+45^o). Здесь воспользуемся формулой косинуса суммы:
$$cos(alpha+beta)=cos(30^o)*cos(45^o)-sin(30^0)*sin(45^0)=$$
$$=frac{sqrt{3}}{2}*frac{sqrt{2}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что (cos(75^o)=sin(15^o)). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.
Ответ: (cos(75^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Мы не будем выводить эти формулы – это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.
Формулы двойного угла
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$
Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол (2alpha) через (alpha). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :
$$cos(2alpha)=cos(alpha+alpha)=cos(alpha)*cos(alpha)-sin(alpha)*sin(alpha)=cos(alpha)^2-sin(alpha)^2;$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=1-sin(alpha)^2-sin(alpha)^2=1-2sin(alpha)^2;$$
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=cos(alpha)^2-(1-cos(alpha)^2)=2cos(alpha)^2-1;$$
Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$sin(2alpha)=sin(alpha)*cos(alpha)+sin(alpha)*cos(alpha)=2sin(alpha)cos(alpha);$$
Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2alpha)=frac{sin(2alpha)}{cos(2alpha)}=frac{2sin(alpha)cos(alpha)}{cos(alpha)^2-sin(alpha)^2}=frac{frac{2sin(alpha)cos(alpha)}{cos(alpha)^2}}{frac{cos(alpha)^2-sin(alpha)^2}{cos(alpha)^2}}=frac{frac{2sin(alpha)}{cos(alpha)}}{1-frac{sin(alpha)^2}{cos(alpha)^2}}=frac{2tg(alpha)}{1-tg(alpha)^2};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2alpha)=frac{cos(2alpha)}{sin(2alpha)}=frac{cos(alpha)^2-sin(alpha)^2}{2sin(alpha)cos(alpha)}=frac{frac{cos(alpha)^2-sin(alpha)^2}{sin(alpha)^2}}{frac{2sin(alpha)cos(alpha)}{sin(alpha)^2}}=frac{frac{cos(alpha)^2}{sin(alpha)^2}-1}{frac{2cos(alpha)}{sin(alpha)}}=frac{ctg(alpha)^2-1}{2ctg(alpha)};$$
В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:
Пример 6
Найти значение (24cos(2alpha)=?), если (sin(alpha)=-0,2.)
Воспользуемся формулой косинуса двойного угла:
$$cos(2alpha)=1-2sin(alpha)^2;$$
$$24cos(2alpha)=24(1-2sin(alpha)^2)=24-48sin(alpha)^2=24-48*(-0,2)^2=24-48*0,04=22,08.$$
Пример 7
Найти значение (frac{10sin(6alpha)}{3cos(3alpha)}=?), если (sin(3alpha)=0,6.)
Используем синус двойного угла, для этого представим (6alpha=2*(3alpha)):
$$sin(6alpha)=sin(2*(3alpha))=2sin(3alpha)cos(3alpha);$$
$$frac{10sin(6alpha)}{3cos(3alpha)}=frac{10*2sin(3alpha)cos(3alpha)}{3cos(3alpha)}=frac{20sin(3alpha)}{3}=frac{20*0,6}{3}=frac{12}{3}=4.$$
Пример 8
Найти значение выражения (frac{12sin(11^o)cos(11^o)}{sin(22^o)}=?)
Замечаем, что (22^o=2*11^o) и воспользуемся синусом двойного угла:
$$frac{12sin(11^o)cos(11^o)}{sin(22^o)}=frac{12sin(11^o)cos(11^o)}{2sin(11^o)cos(11^o)}=frac{12}{2}=6.$$
Формулы тройного угла
Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$
Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$cos(3*alpha)=cos(2alpha+alpha)=cos(2alpha)*cos(alpha)-sin(2alpha)*sin(alpha)=$$
$$=(cos(alpha)^2-sin(alpha)^2)*cos(alpha)-2sin(alpha)*cos(alpha)*sin(alpha)=$$
$$=cos(alpha)^3-sin(alpha)^2*cos(alpha)-2sin(alpha)^2*cos(alpha)=$$
$$=cos(alpha)^3-3sin(alpha)^2*cos(alpha);$$
Если расписать (sin(alpha)^2=1-cos(alpha)^2), то получим еще один вариант формулы тройного угла:
$$cos(3*alpha)=cos(alpha)^3-3sin(alpha)^2*cos(alpha)=cos(alpha)^3-3(1-cos(alpha)^2)*cos(alpha)=$$
$$=4cos(alpha)^3-3cos(alpha);$$
Аналогично выводится формула синуса тройного угла:
$$sin(3alpha)=sin(2alpha+alpha)=sin(2alpha)*cos(alpha)+sin(alpha)*cos(2alpha)=$$
$$=2sin(alpha)*cos(alpha)*cos(alpha)+sin(alpha)*(cos(alpha)^2-sin(alpha)^2)=$$
$$=2sin(alpha)*cos(alpha)^2+sin(alpha)*cos(alpha)^2-sin(alpha)^3=3sin(alpha)*cos(alpha)^2-sin(alpha)^3;$$
Распишем по основному тригонометрическому тождеству (cos(alpha)^2=1-sin(alpha)^2) и подставим:
$$sin(3alpha)=3sin(alpha)*cos(alpha)^2-sin(alpha)^3=$$
$$=3sin(alpha)*(1-sin(alpha)^2)-sin(alpha)^3=3sin(alpha)-4sin(alpha)^3;$$
Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.
Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.
Формулы половинного угла (двойного аргумента)
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$
Формулы половинного угла это по сути формулы обратные формулам двойного угла. Достаточно запомнить их элементарный вывод, тогда учить совсем необязательно. Здесь важный момент, что любой угол (alpha) всегда можно представить в виде удвоенного угла (frac{alpha}{2}):
$$alpha=2*frac{alpha}{2};$$
Выведем формулу синуса половинного угла, для этого нам понадобится формула косинуса двойного угла:
$$cos(alpha)=1-2*sin(frac{alpha}{2})^2;$$
Выразим отсюда (sin(frac{alpha}{2})):
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
Иногда эту формулу записывают без квадрата:
$$sin(frac{alpha}{2})=pmsqrt{frac{1-cos(alpha)}{2}};$$
Плюс минус возникает при избавлении от квадрата.
Вывод косинуса половинного угла тоже получается из формулы косинуса двойного угла:
$$cos(alpha)=2*cos(frac{alpha}{2})^2-1;$$
$$cos(frac{alpha}{2})^2=frac{cos(alpha)+1}{2};$$
$$cos(frac{alpha}{2})=pmsqrt{frac{cos(alpha)+1}{2}};$$
Доказательство формул половинного угла для тангенса и котангенса следует из выше доказанных формул:
$$tg(frac{alpha}{2})=frac{sin(frac{alpha}{2})}{cos(frac{alpha}{2})}=frac{pmsqrt{frac{1-cos(alpha)}{2}}}{pmsqrt{frac{cos(alpha)+1}{2}}}=sqrt{frac{frac{1-cos(alpha)}{2}}{frac{cos(alpha)+1}{2}}}=frac{1-cos(alpha)}{1+cos(alpha)};$$
Точно так же для котангенса:
$$сtg(frac{alpha}{2})=frac{cos(frac{alpha}{2})}{sin(frac{alpha}{2})}=frac{pmsqrt{frac{cos(alpha)+1}{2}}}{pmsqrt{frac{1-cos(alpha)}{2}}}=sqrt{frac{frac{cos(alpha)+1}{2}}{frac{1-cos(alpha)}{2}}}=frac{1+cos(alpha)}{1-cos(alpha)};$$
Пример 9
При помощи формул половинного угла можно, например, посчитать (cos(15^o)):
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$cos(15^o)^2=frac{1+cos(30^o)}{2}=frac{1+frac{sqrt{3}}{2}}{2}=frac{2+sqrt{3}}{4};$$
$$cos(15^o)=sqrt{frac{2+sqrt{3}}{4}}.$$
Кстати, формулы половинного угла справедливы не только в явном виде, когда аргумент правой части формулы (alpha), а левой (frac{alpha}{2}). Но и в неявном, достаточно, чтобы аргумент правой части был больше аргумента левой в два раза:
$$sin(5alpha)=pmsqrt{frac{1-cos(10alpha)}{2}};$$
Формулы понижения степени
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$
Формулы понижения второй степени на самом деле дублируют формулы половинного угла.
Формулы понижения третей степени перестановкой слагаемых дублируют формулы тройного угла.
Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$
Формулы для суммы и разности тригонометрических функций полезны, если необходимо превратить сумму двух функций в произведение. Они в основном используются в уравнениях и преобразованиях сложных выражений, когда необходимо слагаемые разложить на множители.
Для вывода формул суммы и разности синусов и косинусов нам понадобится пара трюков и формулы синуса и косинуса суммы и разности (тут можно запутаться, в названиях формул, будьте внимательны). Вывод получается не самый очевидный.
Обратите внимание, что любой угол (alpha) можно представить в таком странном виде:
$$alpha=frac{alpha}{2}+frac{alpha}{2}+frac{beta}{2}-frac{beta}{2}=frac{alpha+beta}{2}+frac{alpha-beta}{2};$$
Аналогично угол (beta):
$$beta=frac{alpha+beta}{2}-frac{alpha-beta}{2};$$
Эти странности нам понадобятся при выводе формул, просто обратите на них внимание.
А теперь перейдем непосредственно к выводу формулы суммы синусов двух углов. Для начала распишем угла (alpha) и (beta) по формулам выше:
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2}); qquad (*)$$
Теперь воспользуемся формулами синуса суммы и синуса разности:
$$sin(gamma+sigma)=sin(gamma)*cos(sigma)+sin(sigma)*cos(gamma);$$
$$sin(gamma-sigma)=sin(gamma)*cos(sigma)-sin(sigma)*cos(gamma);$$
Только у нас под синусами будут стоять не (gamma) и (sigma), а целые выражения.
Пусть:
$$gamma=frac{alpha+beta}{2};$$
$$sigma=frac{alpha-beta}{2};$$
Применим формулы синуса суммы и разности в (*):
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2})=$$
$$=left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})+sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)+$$
$$+left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})-sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)=$$
$$=2*sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2}); $$
В самом конце мы просто раскрыли большие скобки и привели подобные слагаемые.
Аналогично выводятся все остальные формулы.
Пример 10
Вычислить (sin(165)+sin(75)=?)
(165^o) и (75^o) это не табличные углы. Значения синусов этих углов мы не знаем. Для решения этого примера воспользуемся формулой суммы синусов:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(165^o)+sin(75^o)=2*sinleft(frac{165^o+75^o}{2}right)*cosleft(frac{165^o-75^o}{2}right)=$$
$$=2*sin(120^o)*cos(45^o)=2*frac{sqrt{3}}{2}*frac{sqrt{2}}{2}=frac{sqrt{6}}{2}.$$
Преобразование произведения тригонометрических функций
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$
В некотором смысле формулы произведения синуса, косинуса, тангенса и котангенса являются обратными к тригонометрическим формулам суммы и разности тригонометрических функций. При помощи этих формул возможно перейти от произведения к сумме или разности.
Для вывода нам опять понадобятся формулы косинуса суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим эти две формулы. Для этого складываем их левые части и приравниваем сумме правых частей:
$$cos(alpha+beta)+cos(alpha-beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha)+cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Приводим подобные слагаемые:
$$cos(alpha+beta)+cos(alpha-beta)=2*cos(alpha)*cos(beta);$$
Отсюда получаем:
$$cos(alpha)*cos(beta)=frac{1}{2}*(cos(alpha+beta)+cos(alpha-beta));$$
Формула произведения косинусов доказана.
Произведение синусов доказывается похожим образом. Для этого домножим формулу косинуса суммы слева и справа на ((-1)):
$$-cos(alpha+beta)=-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Косинус разности оставим без изменений:
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим опять эти две формулы:
$$cos(alpha-beta)-cos(alpha+beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha)-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
$$cos(alpha-beta)-cos(alpha+beta)=2*sin(beta)*sin(alpha);$$
$$sin(beta)*sin(alpha)=frac{1}{2}*(cos(alpha-beta)-cos(alpha+beta));$$
Произведение синусов тоже доказано.
Для того, чтобы вывести формулу произведения синуса и косинуса, нам понадобятся формулы синуса суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
Сложим их:
$$sin(alpha+beta)+sin(alpha-beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha)+sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(alpha+beta)+sin(alpha-beta)=2*sin(alpha)*cos(beta);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
Пример 11
Вычислить (sin(75^o)*cos(15^o)=?)
Воспользуемся формулой произведения синуса и косинуса:
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
$$sin(75^o)*cos(15^o)=frac{1}{2}*(sin(75^o+15^o)+sin(75^o-15^o))=$$
$$=frac{1}{2}*(sin(90^o)+sin(60^o))=frac{1}{2}*(1+frac{sqrt{3}}{2})=frac{2+sqrt{3}}{4}.$$
Запросы «sin» и «синус» перенаправляются сюда; у терминов sin и синус есть также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.
Рис. 1.
Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса
Тригонометри́ческие фу́нкции — элементарные функции[1], которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.
Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям традиционно причисляют:
- прямые тригонометрические функции:
- синус (
);
- косинус (
);
- производные тригонометрические функции:
- тангенс
;
- котангенс
;
- секанс
;
- косеканс
;
- обратные тригонометрические функции:
- арксинус, арккосинус и т. д.
В типографике литературы на разных языках сокращённое обозначение тригонометрических функций различно, например, в англоязычной литературе тангенс, котангенс и косеканс обозначаются 


Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции (версинус и т. д.).
Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначны, периодичны и бесконечно дифференцируемы, за исключением счётного числа разрывов второго рода: у тангенса и секанса в точках 

Графики тригонометрических функций показаны на рис. 1.
Способы определения[править | править код]
Определение для любых углов[править | править код]
Рис. 2.
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически[3]. В декартовой системе координат на плоскости построим окружность единичного радиуса (






Синусом угла 






Косинусом угла 






Тангенсом угла 


Котангенсом угла 


Таким образом, определения тригонометрических функций выглядят следующим образом:
Нетрудно видеть, что такое определение также основывается на отношениях прямоугольного треугольника, с тем отличием, что учитывается знак (

В тригонометрии удобным оказывается вести счёт углов не в градусной мере, а в радианной. Так, угол в 






Наконец, определим тригонометрические функции вещественного числа 

Определение для острых углов[править | править код]
Рис. 4.
Тригонометрические функции острого угла
Определение тангенса. Марка СССР 1961 года
В геометрии тригонометрические функции острого угла определяются отношениями сторон прямоугольного треугольника[5]. Пусть 



Данное определение имеет некоторое методическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач о тупоугольных треугольниках. (См.: теорема синусов, теорема косинусов).
Определение как решений дифференциальных уравнений[править | править код]
Синус и косинус можно определить как единственные функции, вторые производные которых равны самим функциям, взятым со знаком минус:
То есть задать их как чётное (косинус) и нечётное (синус) решения дифференциального уравнения
с дополнительными условиями:


Определение как решений функциональных уравнений[править | править код]
Функции косинус и синус можно определить[7]
как решения (


при дополнительных условиях:




Определение через ряды[править | править код]
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу, и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также равенствами 



где
— числа Бернулли,
— числа Эйлера.
Значения тригонометрических функций для некоторых углов[править | править код]
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («
Значения косинуса и синуса на окружности
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций нестандартных углов[править | править код]
| Радианы | 
|

|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций для некоторых других углов
Свойства тригонометрических функций[править | править код]
Простейшие тождества[править | править код]
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности (
Это соотношение называется основным тригонометрическим тождеством.
Разделив это уравнение на квадрат косинуса и синуса соответственно, получим:
Из определения тангенса и котангенса следует, что
Любую тригонометрическую функцию можно выразить через любую другую тригонометрическую функцию с тем же аргументом (с точностью до знака из-за неоднозначности раскрытия квадратного корня). Нижеприведённые формулы верны для 
| sin | cos | tg | ctg | sec | cosec | |
|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Непрерывность[править | править код]
Чётность[править | править код]
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность[править | править код]
Функции 




Формулы приведения[править | править код]
Формулами приведения называются формулы следующего вида:
Здесь 



или что то же самое:
Некоторые формулы приведения:

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Интересующие формулы приведения так же могут легко быть получены рассмотрением функций на единичной окружности.
Формулы сложения и вычитания[править | править код]
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов[править | править код]
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
следует из формулы дополнения и формулы Гаусса для гамма-функции.
Из формулы Муавра можно получить следующие общие выражения для кратных углов:
где ![[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)


Формулы половинного угла:
Произведения[править | править код]
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени[править | править код]
Иллюстрация равенства
Суммы[править | править код]
Существует представление:
где угол 
Универсальная тригонометрическая подстановка[править | править код]
Все тригонометрические функции можно выразить через тангенс половинного угла:






Исследование функций в математическом анализе[править | править код]
Разложение в бесконечные произведения[править | править код]
Тригонометрические функции могут быть представлены в виде бесконечного произведения многочленов:
Эти соотношения выполняются при любом значении 
Непрерывные дроби[править | править код]
Разложение тангенса в непрерывную дробь:
Производные и первообразные[править | править код]
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:






Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом[8]:






Тригонометрические функции комплексного аргумента[править | править код]
Определение[править | править код]
Формула Эйлера:
Формула Эйлера позволяет определить тригонометрические функции от комплексных аргументов через экспоненту по аналогии с гиперболическими функциями, или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
где
Соответственно, для вещественного x:
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики[править | править код]
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
|
|
|
|
|
|
|

|

|

|

|

|

|
История названий[править | править код]
Линия синуса (линия 
Современные краткие обозначения 

Термины «тангенс» (лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
Позднее были введены и термины для обратных тригонометрических функций — арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс — с помощью добавления приставки «арк» (от лат. arcus — дуга), — Ж. Лагранжем и др.
См. также[править | править код]
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Интегральный секанс
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Тригонометрические тождества
- Тригонометрические функции от матрицы
- Тригонометрический ряд Фурье
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература[править | править код]
- Бермант А. Ф., Люстерник Л. А. Тригонометрия. — М.: Наука, 1967.
- Тригонометрические функции — статья из Большой советской энциклопедии. — М.: Советская энциклопедия, 1977. — Т. 26. — С. 204—206.
- Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6 www.alleng.ru/d/math/math42.htm
- Двайт Г. Б. Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
- Кожеуров П. А. Тригонометрия. — М.: Физматгиз, 1963.
- Маркушевич А. И. Замечательные синусы. — М.: Наука, 1974.
- Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1984. — И. М. Виноградов. Тригонометрические функции // Математическая энциклопедия. — М.: Советская энциклопедия. — 1977—1985.
- Тригонометрические функции // Энциклопедический словарь юного математика / Ред. коллегия, Гнеденко Б. В. (гл. ред.), Савин А. П. и др. — М.: Педагогика, 1985 (1989). — С. 299—301—305. — 352 с., ил. — ISBN 5-7155-0218-7 (С. 342, 343 — таблицы тригонометрических функций 0°-90°, в том числе в радианах)
- Тригонометрические функции // Справочник по математике (для ср. уч. заведений) / Цыпкин А. Г., под ред. Степанова С. А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 240—258. — 480 с.
Ссылки[править | править код]
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Trigonometric Functions (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций (в том числе нахождение углов треугольника по сторонам)
- Интерактивная карта значений тригонометрических функций
- Тригонометрические таблицы (0° — 360°)
- «Синус и косинус — это проценты» — перевод статьи How To Learn Trigonometry Intuitively | BetterExplained (англ.)
Примечания[править | править код]
- ↑ Справочник: Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с. Архивная копия от 19 января 2015 на Wayback Machine относит их к специальным функциям.
- ↑ Знак математический. // Большая советская энциклопедия. 1-е изд. Т. 27. — М., 1933.
- ↑ Справочник по элементарной математике, 1978, с. 282—284.
- ↑ Шахмейстер А. Х. Определение основных тригонометрических функций // Тригонометрия : [рус.] : книга / А. Х. Шахмейстер; под ред. Б. Г. Зива. — 3-е изд., стереотипное. — М. : Издательство МЦНМО ; СПб. : «Петроглиф» : «Виктория плюс», 2013. — С. 11, 14, 18, 20. — 752 с. : илл. — (Математика. Элективные курсы). — 1500 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-4439-0050-6. — ISBN 978-5-98712-042-2. — ISBN 978-5-91673-097-5.
- ↑ Справочник по элементарной математике, 1978, с. 271—272.
- ↑ Латинско-русский словарь. Дата обращения: 9 апреля 2023.
- ↑ Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. 1. — М.: Наука, 1998. — ISBN 5-02-015231-5.
- ↑ В формулах, содержащих логарифм в правой части равенств, константы интегрирования
, вообще говоря, различны для различных интервалов непрерывности.
определение, формула, таблица, график, свойства
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Тригонометрическая функция: Косинус угла (cos)
- Определение
- График косинуса
- Свойства косинуса
- Обратная к косинусу функция
- Таблица косинусов
Определение
Косинус острого угла α (cos α) – это отношение прилежащего катета (b) к гипотенузе (c) в прямоугольном треугольнике.
cos α = b / c
Например:
b = 4
c = 5
cos α = b / c = 4 / 5 = 0.8
График косинуса
Функция косинуса пишется как y = cos (x). График называется косинусоидой и в общем виде выглядит следующим образом:
Косинусоида – периодическая функция с основным периодом T = 2π.
Свойства косинуса
Ниже в табличном виде представлены основные свойства косинуса с формулами:
| Свойство | Формула | ||||
| Симметричность | cos (-α) = cos α | ||||
| Симметричность | cos (90°- α) = sin α | ||||
| Пифагорейская тригонометрическая идентичность | sin2 α + cos2 α = 1 | ||||
| cos α = sin α / tg α | |||||
| cos α = 1 / sec α | |||||
| Косинус двойного угла | cos 2α = cos2α — sin2α | ||||
| Косинус суммы углов | cos (α+β) = cos α cos β — sin α sin β | ||||
| Косинус разности углов | cos (α-β) = cos α cos β + sin α sin β | ||||
| Сумма косинусов | Разность косинусов | Произведение косинусов | Произведение косинуса и синуса | Производная косинуса | cos’ x = -sin x |
| Интеграл косинуса | ∫ cos x dx = sin x + C | ||||
| Формула Эйлера | cos x = (eix + e—ix) / 2 |
microexcel.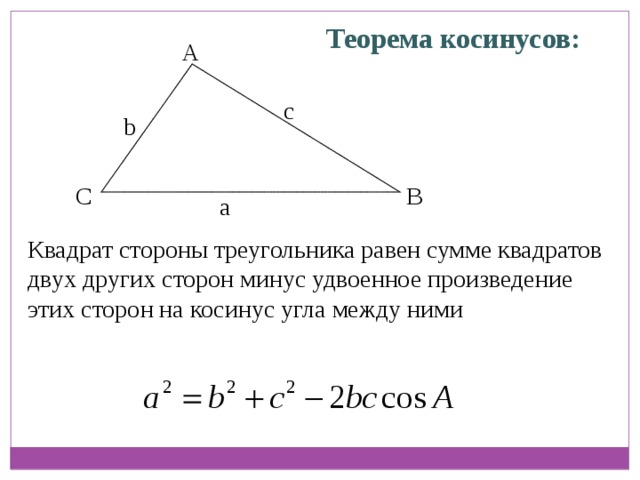
Обратная к косинусу функция
Арккосинус x – это обратная к косинусу функция x, при -1≤x≤1.
Если косинус у равняется х (cos y = x), значит арккосинус x равен у:
arccos x = cos-1 x = y
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
Таблица косинусов
| x (°) | x (рад) | cos x |
| 180° | π | -1 |
| 150° | 5π/6 | -√3/2 |
| 135° | 3π/4 | -√2/2 |
| 120° | 2π/3 | -1/2 |
| 90° | π/2 | 0 |
| 60° | π/3 | 1/2 |
| 45° | π/4 | √2/2 |
| 30° | π/6 | √3/2 |
| 0° | 0 | 1 |
microexcel.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Формула вычисления косинуса угла между векторами
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.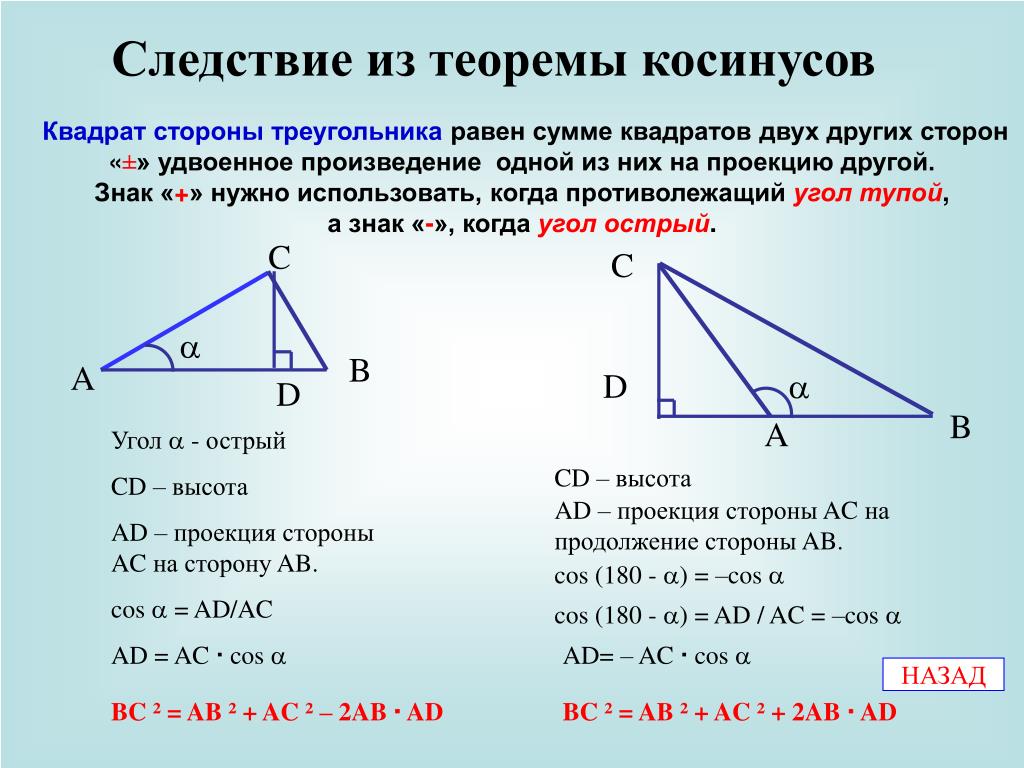
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Формула
Чтобы найти косинус угла между векторами нужно найти отношение скалярного произведения векторов и произведение их длин (модулей). Если векторы заданы на плоскости двумя координатами $ overline=(x_1;y_1) $ и $ overline=(x_2;y_2) $, то косинус угла между ними вычисляется по формуле:
В числителе находится скалярное произведение векторов, то есть каждая координата умножается на соответствующую координату другого вектора и при этом находится сумма всех произведений. А в знаменателе расположено произведение модулей векторов. Каждый модуль равен извлеченному квадратному корню из суммы квадратов координат вектора.
Примеры решений
Напомним как найти косинус угла между векторами. Необходимо определить на плоскости или в пространстве находятся векторы, то есть сколько у них координат. Затем воспользоваться подходящей формулой.
Первым делом вычисляем скалярное произведение: каждую координату одного вектора умножаем на соответствующую координату другого вектора, а потом суммируем произведения:
Далее находим чему равны модули каждого из векторов:
Теперь можно найти косинус угла между векторами подставив найденные значения в первую формулу:
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
| Пример |
| Даны два вектора $ overline =(3;1) $ и $ overline = (2;4) $.  Требуется найти косинус угла между векторами. Требуется найти косинус угла между векторами. |
| Решение |
примеры и решения, как найти косинус угла между векторами, вычислите угол между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Нахождение сторон треугольника через синус и косинус. Теорема Пифагора, чтобы найти катет прямоугольного треугольника
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу.
Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
Площадь треугольника равна половине произведения его сторон на синус угла между ними.
Доказательство:
Рассмотрим произвольный треугольник ABC.
.
Для начала введем прямоугольную систему координат и поместим начало координат в точку С. Расположим нашу систему координат так, чтобы точка B лежала на положительном направлении оси Сх, а точка А имела бы положительную ординату.
Если все выполнить правильно, то должен получится следующий рисунок.
Площадь данного треугольника можно вычислить по следующей формуле: S = (1/2)*a*h
, где h — это высота треугольника. В нашем случае высота треугольника h равна ординате точки А, то есть h = b*sin(C).
Учитывая полученные результат, формулу площади треугольника можно переписать следующим образом: S = (1/2)*a*b*sin(C). Что и требовалось доказать.
Решение задач
Задача 1. Найти площадь треугольника ABC, если а) AB = 6*√8 см, АС = 4 см, угол А = 60 градусов б) BC = 3 см, AB = 18*√2 см, угол B= 45 градусов в) AC = 14 см, CB = 7 см, угол C= 48 градусов.
Положим S — площадь треугольника ABC. По теореме о площади треугольника имеем:
S = (1/2)*AB*AC*sin(A).
Подставим в неё имеющиеся у нас значения:
60 = (1/2)*AB*15*sin30˚ = (1/2)*15*(1/2)*AB=(15/4)*AB.
Отсюда выражаем длину стороны AB: AB = (60*4)/15 = 16.
Сторону
треугольника дозволено обнаружить не только по периметру и площади, но и по заданной стороне и углам. Для этого применяются тригонометрические функции –
синус
и косинус
. Задачи с их применением встречаются в школьном курсе геометрии, а также в вузовском курсе аналитической геометрии и линейной алгебры.
Инструкция
1.
Если знаменита одна из сторон треугольника и угол между ней и иной его стороной, воспользуйтесь тригонометрическими функциями – синус
ом и косинус
ом. Представьте себе прямоугольный треугольник НBC , у которого угол? равен 60 градусам. Треугольник НBC показан на рисунке.
, как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус
– отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?
2.
Если в условии задачи, напротив, дан катет треугольника, обнаружьте его гипотенузу, руководствуясь дальнейшим соотношением между заданными величинами:BC=НB/sin ?По аналогии обнаружьте стороны треугольника и с применением косинус
а, изменив предыдущее выражение дальнейшим образом:cos ?=НC/BC
3.
В элементарной математике существует представление теоремы синус
ов. Руководствуясь фактами, которые описывает данная теорема, также дозволено обнаружить стороны треугольника. Помимо этого, она разрешает обнаружить стороны треугольника, вписанного в окружность, если знаменит вестим радиус последней.
Геометрическая фигура, состоящая из трёх точек, не принадлежащих одной прямой называемых вершинами, и трёх попарно соединяющих их отрезков, называемых сторонами, именуется треугольником. Существует уйма задач на нахождение сторон и углов треугольника по ограниченному числу начальных данных, одна из таких задач – нахождение стороны треугольника по одной из его сторон и двум
углам
.
Инструкция
1.
Пускай построен треугольник?ABC и знамениты – сторона BC и углы?? и??.Знаменито, что сумма углов всякого треугольника равна 180?, следственно в треугольнике?ABC угол?? будет равен?? = 180? – (?? + ??).Обнаружить стороны AC и AB дозволено применяя теорему синусов, которая гласитAB/sin?? = BC/sin?? = AC/sin?? = 2 * R, где R – радиус описанной около треугольника?ABC окружности,тогда получаемR = BC/sin??,AB = 2 * R * sin??,AC = 2 * R * sin??.Теорему синусов дозволено использовать при всяких данных 2-х углах и стороне.
2.
Стороны заданно треугольника дозволено обнаружить, вычислив его площадь по формулеS = 2 * R? * sin?? * sin?? * sin??,где R вычисляется по формулеR = BC/sin??, R – радиус описанной около треугольника?ABC отсюдаТогда
сторону
AB дозволено обнаружить, вычислив высоту, опущенную на неёh = BC * sin??,отсель по формуле S = 1/2 * h * AB имеемAB = 2 * S/hАналогичным образом дозволено вычислить сторону
AC.
3.
Если в качестве углов даны внешние углы треугольника?? и??, то обнаружить внутренние углы дозволено с поддержкой соответствующих соотношений?? = 180? – ??,?? = 180? – ??,?? = 180? – (?? + ??).Дальше действуем подобно первым двум пунктам.
Постижение треугольников ведется математиками на протяжении нескольких тысячелетий. Наука о треугольниках – тригонометрия – использует особые величины: синус и косинус.
Прямоугольный треугольник
Изначально синус и косинус появились из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было подмечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается неизменно идентичным.Именно так и были введены представления синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут использоваться не только в прямоугольных треугольниках.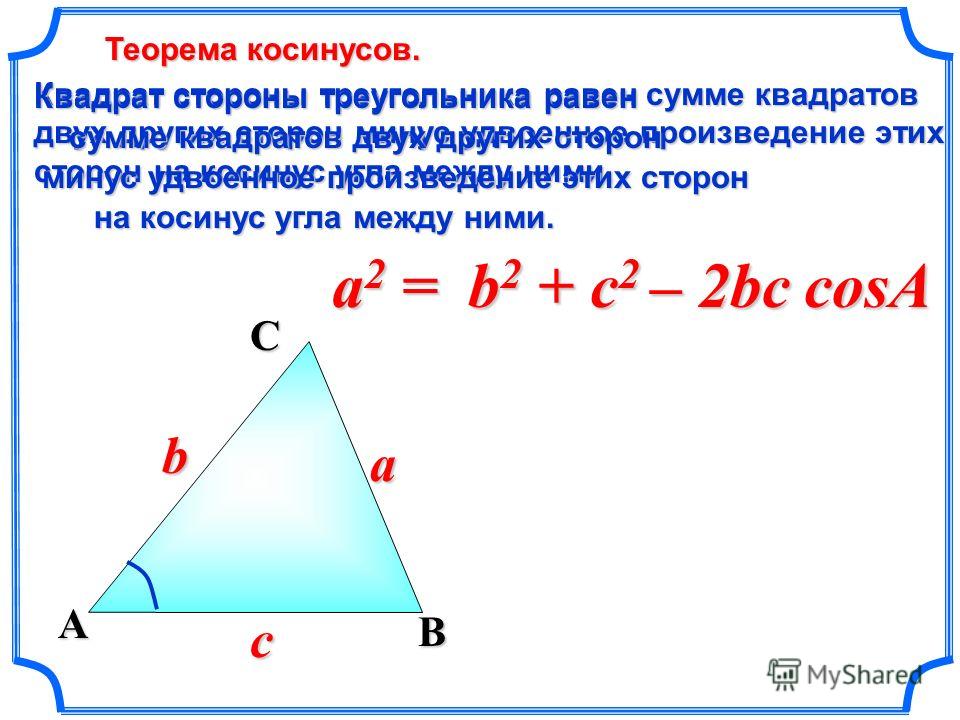
Производные
Производная – математический инструмент, показывающий, как стремительно меняется функция касательно метаморфозы ее довода. Производные применяются в алгебре, геометрии, экономике и физике, ряде технических дисциплин. При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса.
Применение в математике
Особенно зачастую синусы и косинусы применяются при решении прямоугольных треугольников и задач, связанных с ними. Удобство синусов и косинусов обнаружило свое отражение и в технике. Углы и стороны было примитивно оценивать по теоремам косинусов и синусов, разбивая трудные фигуры и объекты на «примитивные» треугольники. Инженеры и архитекторы, зачастую имеющие дело с расчетами соотношения сторон и градусных мер, тратили много времени и усилий для вычисления косинусов и синусов не табличных углов. Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов различных углов. В советское время некоторые преподаватели принуждали своих подопечных учить страницы таблиц Брадиса назубок.
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.
Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По синус угла в 30° равен 0.5
Площадь треугольника будет равна 3 кв. см.
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:
Площадь будет равна половине квадрата стороны, умноженной на дробь.
Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Подставляем данные в формулу
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать .
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
Из теоремы выводим формулы для поиска длины неизвестной стороны:
Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°. Для начала найдем недостающую сторону с
. По косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов.
Теперь используя формулу, найдем
Основное тригонометрическое тождество
12 ноября 2011
Это последний и самый главный урок, необходимый для решения задач B11. Мы уже знаем, как переводить углы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а также умеем определять знак тригонометрической функции, ориентируясь по координатным четвертям (см. урок «Знаки тригонометрических функций»).
Дело осталось за малым: вычислить значение самой функции — то самое число, которое записывается в ответ. Здесь на помощь приходит основное тригонометрическое тождество.
Основное тригонометрическое тождество.
Для любого угла α верно утверждение:
sin2 α + cos2 α = 1.
Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Обратите внимание на знак «±» перед корнями. Дело в том, что из основного тригонометрического тождества непонятно, каким был исходный синус и косинус: положительным или отрицательным. Ведь возведение в квадрат — четная функция, которая «сжигает» все минусы (если они были).
Именно поэтому во всех задачах B11, которые встречаются в ЕГЭ по математике, обязательно есть дополнительные условия, которые помогают избавиться от неопределенности со знаками. Обычно это указание на координатную четверть, по которой можно определить знак.
Внимательный читатель наверняка спросит: «А как быть с тангенсом и котангенсом?» Напрямую вычислить эти функции из приведенных выше формул нельзя. Однако существуют важные следствия из основного тригонометрического тождества, которые уже содержат тангенсы и котангенсы.
Важное следствие: для любого угла α можно переписать основное тригонометрическое тождество следующим образом:
Эти уравнения легко выводятся из основного тождества — достаточно разделить обе стороны на cos2 α (для получения тангенса) или на sin2 α (для котангенса).
Рассмотрим все это на конкретных примерах. Ниже приведены настоящие задачи B11, которые взяты из пробных вариантов ЕГЭ по математике 2012.
Задача. Найдите sin α, если известно следующее:
Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:
sin2 α + cos2 α = 1 ⇒ sin2 α + 99/100 = 1 ⇒sin2 α = 1/100 ⇒sin α = ±1/10 = ±0,1.
Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π/2; π), то в градусной мере это записывается так: α ∈ (90°; 180°).
Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1.
Задача. Найдите cos α, если известно следующее:
Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:
sin2 α + cos2 α = 1 ⇒ 3/4 + cos2 α = 1 ⇒cos2 α = 1/4 ⇒cos α = ±1/2 = ±0,5.
Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α принадлежит промежутку (π 3π/2). Переведем углы из радианной меры в градусную — получим: α ∈ (180°; 270°).
Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.
Задача. Найдите tg α, если известно следующее:
Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:
Получаем: tg α = ±3. Знак тангенса определяем по углу α.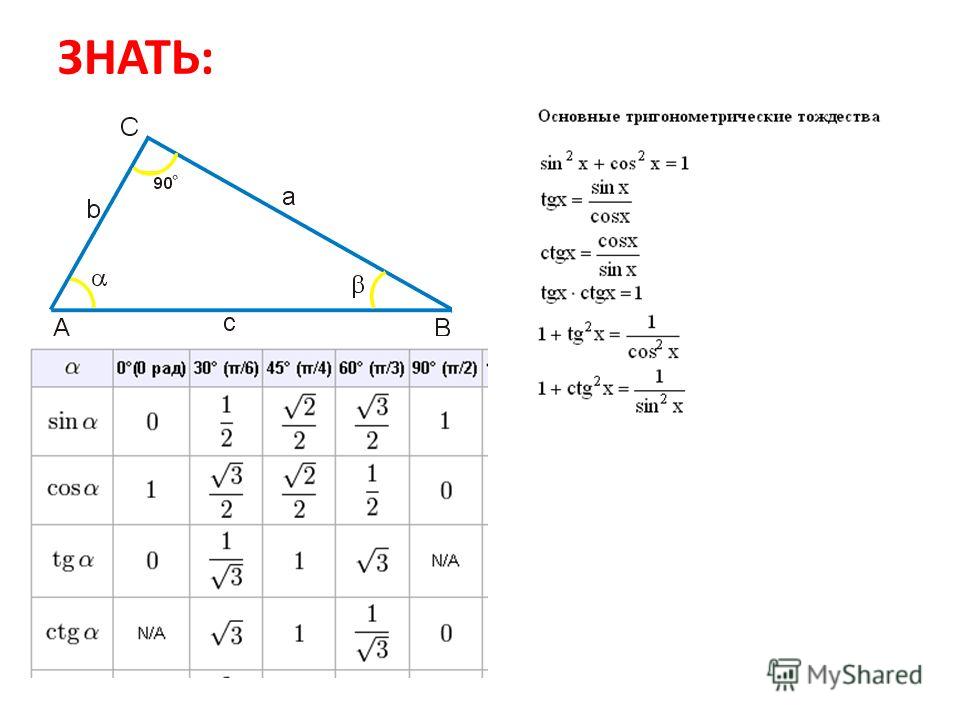
Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.
Задача. Найдите cos α, если известно следующее:
Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:
sin2 α + cos2 α = 1 ⇒ 0,64 + cos2 α = 1 ⇒cos2 α = 0,36 ⇒cos α = ±0,6.
Знак определяем по углу. Имеем: α ∈ (3π/2; 2π). Переведем углы из градусной меры в радианную: α ∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α = 0,6.
Задача. Найдите sin α, если известно следующее:
Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:
Отсюда получаем, что sin2 α = 1/25, т.е. sin α = ±1/5 = ±0,2.
Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2.
Смотрите также:
- Как формулы приведения работают в задаче B11
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Тест к параграфу «Что такое логарифм» (легкий)
- Решение задач B12: №440—447
- Задачи про температуру и энергию звезд
- Задача B4 про шерсть и свитер
Как найти косинус угла между двумя векторами
Формула
Чтобы найти косинус угла между векторами нужно найти отношение скалярного произведения векторов и произведение их длин (модулей). Если векторы заданы на плоскости двумя координатами $ overline=(x_1;y_1) $ и $ overline=(x_2;y_2) $, то косинус угла между ними вычисляется по формуле:
В числителе находится скалярное произведение векторов, то есть каждая координата умножается на соответствующую координату другого вектора и при этом находится сумма всех произведений.
Примеры решений
Напомним как найти косинус угла между векторами. Необходимо определить на плоскости или в пространстве находятся векторы, то есть сколько у них координат. Затем воспользоваться подходящей формулой.
Первым делом вычисляем скалярное произведение: каждую координату одного вектора умножаем на соответствующую координату другого вектора, а потом суммируем произведения:
Далее находим чему равны модули каждого из векторов:
Теперь можно найти косинус угла между векторами подставив найденные значения в первую формулу:
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение.
| Пример |
| Даны два вектора $ overline =(3;1) $ и $ overline = (2;4) $. Требуется найти косинус угла между векторами. |
| Решение |
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.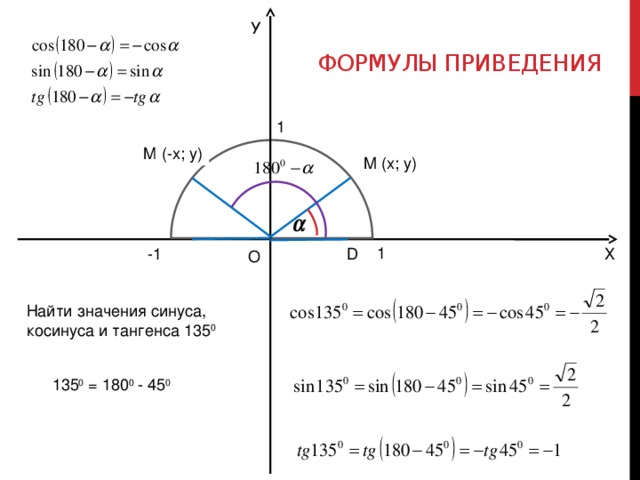
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми.
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Формула косинуса
— Что такое формулы косинуса? Примеры
Формулы косинуса — это формулы функции косинуса в тригонометрии. Функция косинуса (которую обычно называют «cos») — это одна из 6 тригонометрических функций, представляющая собой отношение прилежащего катета к гипотенузе. Существует несколько формул, связанных с функцией косинуса, которые можно вывести из различных тригонометрических тождеств и формул. Давайте изучим формулы косинуса вместе с несколькими решенными примерами.
Что такое формулы косинуса?
Формулы косинуса говорят о функции косинуса (cos). Рассмотрим прямоугольный треугольник, один из острых углов которого равен х. Тогда формула косинуса: cos x = (прилежащая сторона) / (гипотенуза), где «прилежащая сторона» — это сторона, примыкающая к углу x, а «гипотенуза» — это самая длинная сторона (сторона, противоположная прямому углу) треугольник.
Формулы косинуса с использованием тождества обратной величины
Мы знаем, что функция косинуса (cos) и функция секущей (sec) являются обратными величинами. т. е. если cos x = a/b, то sec x = b/a. Таким образом, формула косинуса с использованием одного из обратных тождеств имеет вид
cos x = 1 / (sec x)
Формулы косинуса с использованием тождества Пифагора
Одно из тригонометрических тождеств говорит о связи между sin и cos. Там написано: sin 2 x + cos 2 х = 1, для любого х. Мы можем решить это для cos x.
Рассмотрим SIN 2 X + COS 2 x = 1
Вычитание SIN 2 x с обеих сторон,
COS 2 x = 1 — SIN 2 x
Квадратный корень на обеих стороны,
cos x = ± √(1 — sin 2 x)
Формула косинуса с использованием тождеств кофункций
Тождества кофункций определяют отношение между кофункциями, которые являются sin, cos; sec, csc, tan и cot.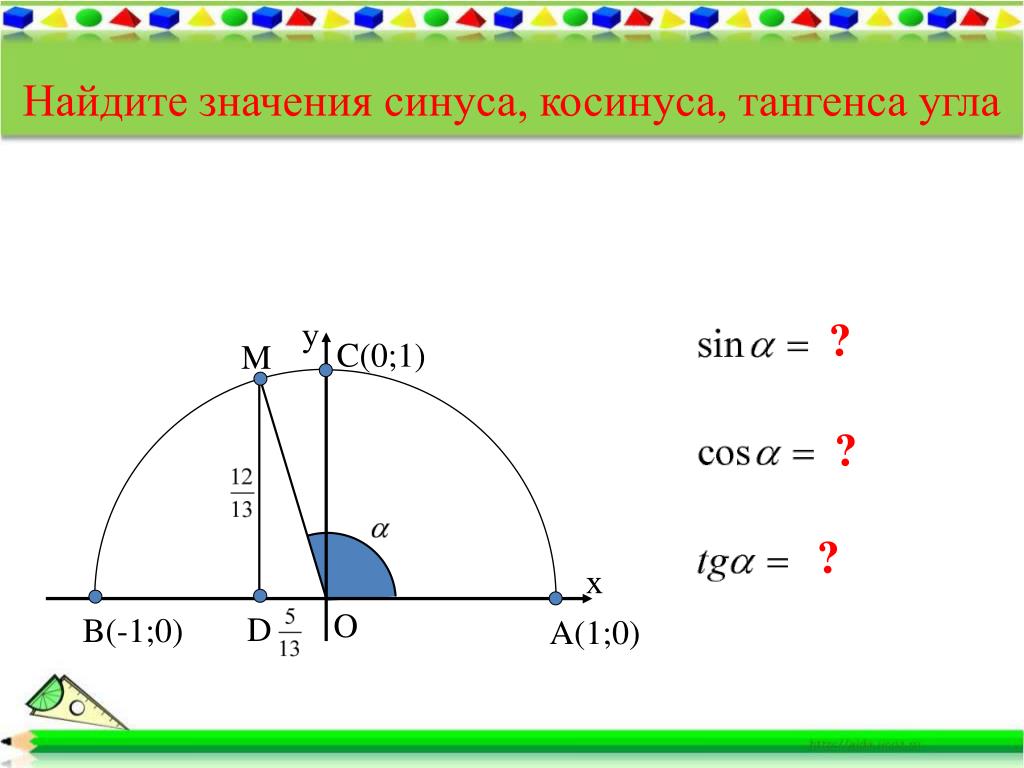
- cos x = sin (90 o — x) (ИЛИ)
- потому что х = грех (π/2 — х)
Формулы косинуса с использованием формул суммы/разности
У нас есть формулы суммы/разности для каждой тригонометрической функции, которая имеет дело с суммой углов (x + y) и разностью углов (x — y). Формулы суммы/разности функции косинуса:
- cos(x + y) = cos (x) cos(y) – sin (x) sin (y)
- cos (x – y) = cos (x) cos (y) + sin (x) sin (y)
Формула косинуса двойного угла
У нас есть формулы двойного угла в тригонометрии, которые имеют дело с двукратным углом. У нас есть несколько формул двойного угла для cos, и мы можем использовать одну из следующих при решении задачи в зависимости от доступной информации.
- cos 2x = cos 2 (x) – sin 2 (x)
- cos 2x = 2 cos 2 (x) − 1
- cos 2x = 1 – 2 sin 2 (x)
- cos 2x = [(1 — тангенс 2 х)/(1 + тангенс 2 х)]
Формула косинуса тройного угла
У нас есть формулы тройного угла для всех тригонометрических функций.
cos 3x = 4 cos 3 x — 3 cos x
Формула косинуса половинного угла
У нас есть формулы половинного угла в тригонометрии, которые имеют дело с половиной углы (x/2). Формула половинного угла функции косинуса:
cos (x/2) =± √[ (1 + cos x) / 2 ]
Формулы косинуса с использованием закона косинусов
Закон косинусов используется для нахождения недостающих сторон/углов в непрямом угле треугольник. Рассмотрим треугольник ABC, в котором AB = c, BC = a и CA = b. Формулы косинуса с использованием закона косинусов:
- cos A = (b 2 + c 2 — a 2 ) / (2bc)
- cos B = (c 2 + a 2 — b 2 ) / (2ac)
- cos C = (a 2 + b 2 — c 2 ) / (2ab)
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.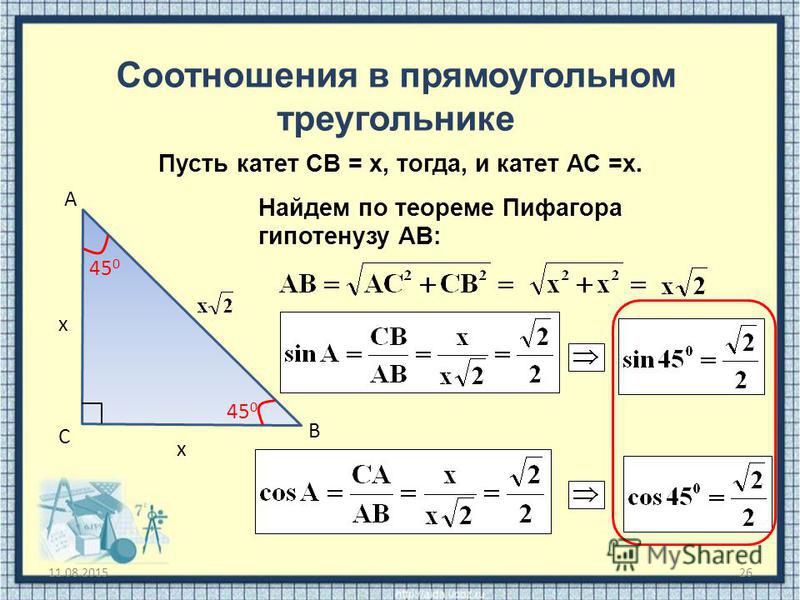
Записаться на бесплатный пробный урок
Примеры формул косинуса
Пример 1: Если sin x = 3/5 и x находится в первом квадранте, найдите значение cos x.
Решение:
Используя одну из формул косинуса,
cos x = ± √(1 — sin 2 x)
Поскольку x находится в первом квадранте, cos x положителен. Таким образом,
cos x = √(1 — sin 2 x)
Подставьте сюда sin x = 3/5,
cos x = √(1 — (3/5) 2 )
= √ (1 — 9/25)
=√ (16/25)
= 4/5
Ответ: , потому что х = 4/5.
Пример 2: Если sin (90 — A) = 1/2, то найдите значение cos A.
Решение:
Используя одну из формул косинуса,
cos A = sin (90 — A)
Дано, что sin (90 — A) = 1/2. Следовательно,
cos A = 1/2
Ответ: cos A = 1/2.
Пример 3: В треугольнике ABC AB = c, BC = a и CA = b. Кроме того, a = 55 единиц, b = 70 единиц и c = 50 единиц. Найдите cos A.
Решение:
Используя формулу косинуса закона косинусов,
cos A = (b 2 + C 2 — A 2 ) / (2BC)
= (70 2 + 50 2 — 55 2 ) / (2 · 70 · 50)
= 5 /5 /5 /5 /5 /5 / 8
Ответ: , потому что A = 5/8.
Часто задаваемые вопросы о формулах косинуса
Что такое формулы косинуса?
Формулы косинуса связаны с функцией косинуса. Важными формулами косинуса являются следующие:
- cos x = (прилежащая сторона) / (гипотенуза)
- cos х = 1 / (сек х)
- cos x = ± √(1 — sin 2 x)
- потому что х = грех (π/2 — х)
Как вывести формулу косинуса половинного угла?
Используя одну из формул двойного угла, cos 2x = 2 cos 2 x — 1.
Каковы применения формул косинуса?
Как мы узнали на этой странице, у нас есть несколько формул косинуса, и мы можем выбрать одну из них, чтобы доказать тригонометрическое тождество (или) найти значение функции косинуса с доступной информацией. Мы можем использовать формулы косинуса, чтобы найти недостающие углы или стороны в треугольнике. Мы также используем формулы косинуса в исчислении.
Как вывести формулу косинуса двойного угла?
Используя формулу суммы функции косинуса, мы имеем, cos(x + y) = cos (x) cos(y) – sin (x) sin (y). Подставив здесь x = y с обеих сторон, мы получим cos 2x = cos 2 x — sin 2 x. Используя тождество Пифагора sin 2 x + cos 2 x = 1, вместе с приведенной выше формулой мы можем вывести две другие формулы косинуса двойного угла: cos 2x = 2 cos 2 (x) − 1 и cos 2x = 1 – 2 грех 2 (х).
Косинус угла – формулы и примеры
Косинус угла находится путем отношения сторон прямоугольного треугольника. Косинус равен длине стороны, примыкающей к углу, деленной на длину гипотенузы. Косинус также равен синусу дополнительного угла. Значения косинусов важнейших углов можно получить, используя пропорции известных треугольников.
Здесь мы более подробно узнаем о косинусе углов и решим некоторые практические задачи.
ТРИГОНОМЕТРИЯ
Актуально для …
Изучение косинуса угла на примерах.
См. примеры
Содержание
ТРИГОНОМЕТРИЯ
Актуально для …
Изучение косинуса угла на примерах.
См. примеры
Определение косинуса угла
Косинус угла прямоугольного треугольника определяется как длина стороны, прилегающей к углу, деленная на длину гипотенузы треугольника. 9{circ}-theta)$
В радианах имеем:
$latex cos (theta)=sin (frac{pi}{2}-theta)$
Прямоугольные треугольники и косинусы
Рассмотрим прямоугольный треугольник ABC с прямым углом C.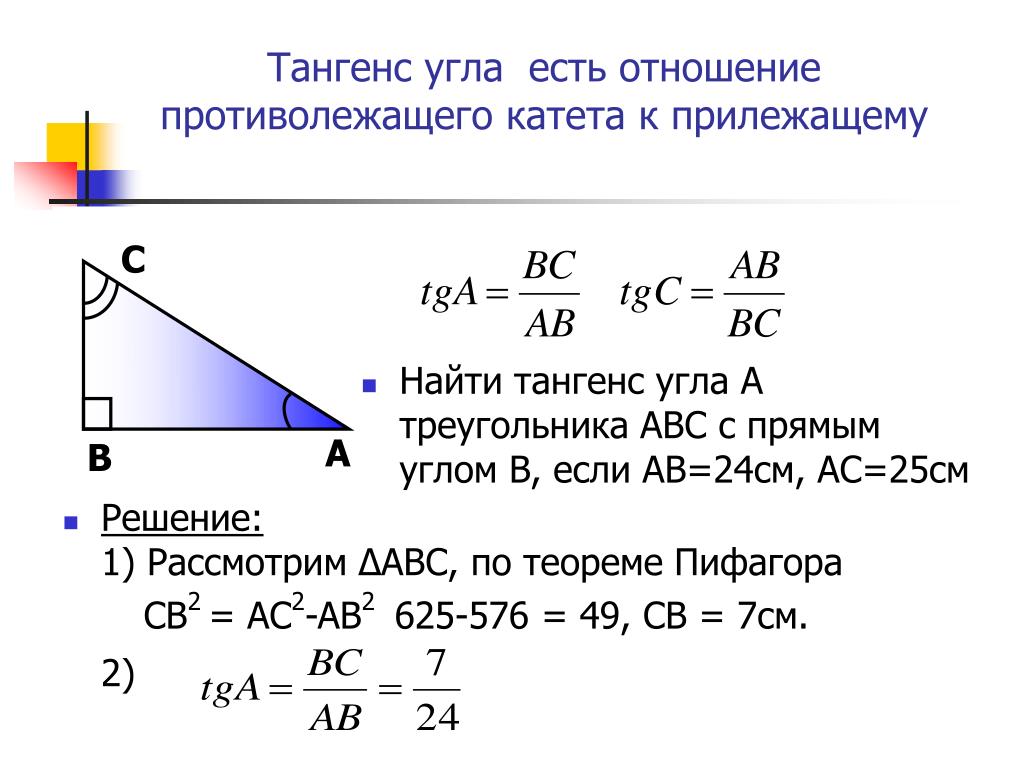
Поскольку сумма внутренних углов треугольника равна 180°, а угол С равен 90°, мы знаем, что углы А и В дополняют друг друга, то есть их сумма составляет 90°. Это означает, что косинус треугольника B равен синусу треугольника A.
Косинус угла прямоугольного треугольника равен прилежащему катету, деленному на гипотенузу:
$latex cos=frac{ text{adjacent}}{text{гипотенуза}}$
В приведенном выше треугольнике $latex cos(A)=frac{b}{c}$, а также $latex cos (B)=frac{a}{c}$. 9{circ}) = frac{sqrt{3}}{2}$.
| Degrees | Radians | Cosine |
| 90° | $latex frac{pi}{2}$ | 0 |
| 60° | $ латекс frac{pi}{3}$ | $latex frac{1}{2}$ |
| 45° | $latex frac{pi}{4}$ | $latex frac {sqrt{2}}{2}$ |
| 30° | $латекс frac{pi}{6}$ | $latex frac{sqrt{3}}{2}$ |
| 0° | 0 | 1 |
Начните сейчас: Изучите наши дополнительные ресурсы по математике Coine An9 9003
Примеры с ответами
Следующие примеры можно использовать, чтобы проследить процесс решения задач, связанных с косинусами.
ПРИМЕР 1
Если $латекс cos(A)=0,2$ и $латекс b = 3$, каково значение $латекс с$?
Решение
Ссылаясь на прямоугольный треугольник выше, мы видим, что мы имеем $latex cos (A) = frac{b}{c}$. Мы можем использовать значения, данные в этом уравнении, и найти c :
$latex cos(A)=frac{b}{c}$
$latex 0.2=frac{3}{c}$
$latex c=frac{3}{0.2}$
$latex c=15$
Значение гипотенузы равно 15.
ПРИМЕР 2
Если $latex a=10$ и $latex cos(B)=frac{1}{3}$, найдите значение $latex c$.
Решение
Из прямоугольного треугольника выше мы можем сделать вывод, что у нас есть $latex cos(B) = frac{a}{c}$. Используя значения, приведенные в формуле, и найдя c, , получим:
$latex cos(B)=frac{a}{c}$
$latex frac{1}{3}= frac{10}{c}$
$latex c=3(10)$
$latex c=30$
Значение гипотенузы равно 30.
ПРИМЕР 3
Каково значение А если у нас есть $латекс b=5$ и $латекс с=8$? 9{-1}}=51,3$°
Угол А равен 51,3°.
→ Калькулятор косинуса (градусы и радианы)
Косинус угла – практические задачи
Применяйте полученные знания о косинусе угла для решения следующих практических задач. Если вам нужна помощь с этим, вы можете посмотреть примеры с ответами выше.
Если у нас $латекс b=2,25$ и $латекс cos(A)=0,15$, каково значение c?
Выберите ответ
$латекс с=10$
$латекс c=12$
$латекс c=13$
$latex c=15$
Если у нас есть $latex a=12$ и $latex cos(B)=frac{1}{3}$, каково значение c?
Выберите ответ
$латекс c=24$
$латекс c=28$
$латекс c=36$
$latex c=42$
Если у нас есть $latex b=6,4$ и $latex c=7,8$, каково значение A?
Выберите ответ
$латекс A=31,7$°
$латекс A=34,9$°
$латекс A=37,4$°
$latex A=41.
См. также
Хотите узнать больше о косинусе угла? Взгляните на эти страницы:
- Калькулятор косинуса (градусы и радианы)
- График косинуса с примерами
- Период функции косинуса – формулы и примеры
- Амплитуда функций косинуса – формулы и примеры
Изучайте математику с помощью наших дополнительных ресурсов по различным темам
УЗНАТЬ БОЛЬШЕ
Что такое формулы косинуса? — GeeksforGeeks
Тригонометрия — это дисциплина математики, изучающая отношения между длинами сторон и углами прямоугольного треугольника. Тригонометрические функции, также известные как гониометрические функции, угловые функции или круговые функции, — это функции, которые устанавливают связь между углом и отношением двух сторон прямоугольного треугольника. Шесть основных тригонометрических функций — это синус, косинус, тангенс, котангенс, секанс и косеканс. Тригонометрические углы — это углы, определяемые соотношениями тригонометрических функций. Тригонометрические углы представляют собой тригонометрические функции. Значение угла может быть где угодно между 0-360°.
Прямоугольный треугольник
Как показано на рисунке выше, в прямоугольном треугольнике:
- Гипотенуза: Сторона, противоположная прямому углу, является гипотенузой. Это самая длинная сторона прямоугольного треугольника. прямоугольного треугольника, противоположного углу 90°.
- Основание: Сторона, на которой лежит угол С, называется основанием.
- Перпендикуляр: Это сторона, противоположная рассматриваемому углу C.
Тригонометрические функции
Тригонометрия имеет 6 основных тригонометрических функций: синус, косинус, тангенс, косеканс, секанс и котангенс. Теперь давайте рассмотрим тригонометрические функции. Шесть тригонометрических функций следующие:
- синус: отношение перпендикуляра к гипотенузе определяется как синус и представляется как sin θ
- косинус: отношение основания к гипотенузе определяется как косинус и представлен как cos θ
- тангенс: соотношение синуса и косинуса угла определяется как тангенс.
Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как тангенс θ.
- косеканс: Это величина, обратная sin θ, обозначается как cosec θ.
- секанс: Это величина, обратная cos θ, обозначается как sec θ.
- Котангенс: Это величина, обратная тангенсу θ, и обозначается как cot θ.
Согласно изображению выше, тригонометрические отношения равны
sin θ = перпендикуляр/гипотенуза = AB/AC
косинус θ = основание/гипотенуза = BC/AC
Ab/bc
cosecant θ = гипотенуза/перпендикулярный = ac/ab
secant θ = гипотенуза/основание = AC/BC
Cotangent θ = основание/перпендикуляр = BC/AB
Обратная идентичность
. θ = 1/ cosec θ ИЛИ cosec θ = 1/ sin θ
cos θ = 1/ с θ ИЛИ с θ = 1 / cos θ
cot θ = 1 / tan θ ИЛИ tan θ = 1 / cot θ
cot θ = Cos θ / sin θ ИЛИ tan sin θ / cos θ
tan θ.
Тригонометрические тождества дополнительных и дополнительных углов
Дополнительные углы: Пара углов, сумма которых равна 90°. Тождества дополнительных углов:
sin (90° – θ) = cos θ
cos (90° – θ) = sin θ
tan (90° – θ) = cot θ
cot (90° – θ) = tan θ
с (90° – θ) = cosec θ
cosec (90 ° – θ) = sec θ
Дополнительные углы: Пара углов, сумма которых равна 180°. Тождества дополнительных углов:
sin (180° – θ) = sin θ
cos (180° – θ) = – cos θ
tan (180° – θ) = – tan θ
3 90 (180° – θ) = – кроватка θ
сек (180° – θ) = – сек θ
cosec (180° – θ) = – cosec θ
Формулы косинуса с использованием тождества Пифагора
Одно из тригонометрических тождеств между sin и cos. Он представляет Sin 2 x + cos 2 x = 1
SIN 2 X + COS 2 x = 1
Теперь вычитая грех 2 x с обеих сторон,
Cos 2 x = 1 – sin 2 x
теперь квадрат с обеих сторон
cos x = ± √(1 – sin 2 x)
Формулы косинуса с формулами суммы/разности
+ y) и разности углов (x – y).

Формулы функции косинуса с формулами разности сумм: cos (x) cos (y) + sin (x) sin (y)
Формулы косинуса с использованием закона косинусов
Этот закон используется для нахождения недостающих сторон/углов в непрямоугольном треугольнике. Предположим, треугольник ABC, в котором AB = c, BC = a и CA = b.
Косинутные формулы —
COS A = (B 2 + C 2 — A 2 )/(2BC)
COS B = (C 2 + A 2 2020202020202020202 – b 2 )/(2ac)
cos C = (a 2 + b 2 – c 2 )/(2ab)
Формула косинуса двойного угла
В тригонометрии при работе с двукратным углом. Существует несколько видов формул косинуса двойного угла, и, исходя из этого, мы используем одну из следующих при решении задачи в зависимости от доступной информации.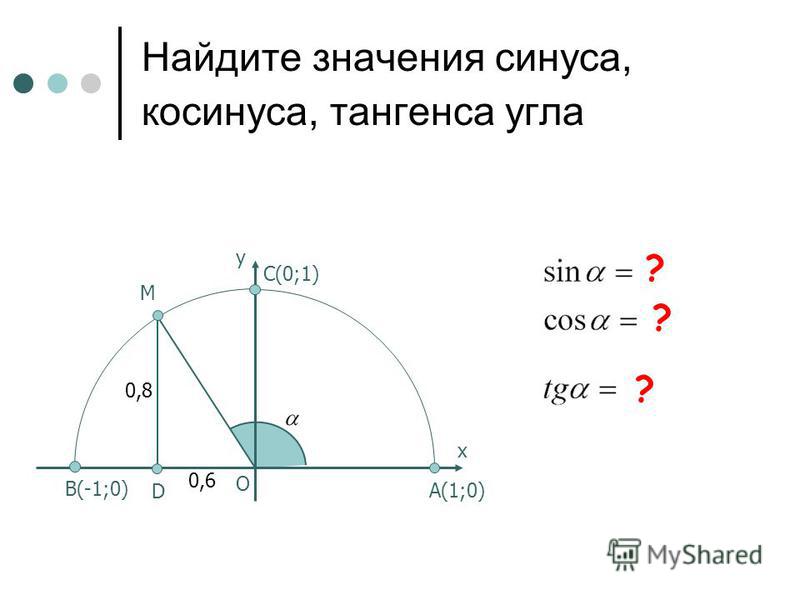
cos 2x = cos 2 (x) – sin 2 (x)
cos 2x = 2 cos 2 (x) − 1
cos 2x = 1 – 2 sin 2 (x)
cos 2x = [(1 – tan 2 x)/(1 + 1 tan 20 x) 90 90 ]
Формула тройного угла косинуса
COS 3X = 4COS 3 x — 3COSX
Проблемы выборки
. Проблема 1: if A = 3/5. первом квадранте, найдите значение cos a.
Решение:
Используя одну из формул косинуса,
cos a = ± √(1 – sin 2 a)
Поскольку a находится в первом квадранте, cos a положителен. Таким образом,
cos a = √(1 – sin 2 a)
Подставим здесь sin a = 3/5, = √(1 – 9/25)
cos a =√ (16/25)
cos a = 4/5
Задача 2: Если sin (90 – A) = 2/3, то найти значение cos A.
Решение:
Используя одну из формул косинуса,
cos A = sin (90 – A)
при условии, что sin (90 – A) = 2/3. Следовательно,
cos A = 2/3
Значение cos A равно 1/2.
Задача 3. В треугольнике ABC AB = c, BC = a и CA = b. Кроме того, a = 50 единиц, b = 60 единиц и c = 30 единиц. Найдите cos A.
Решение:
Используя формулу косинуса закона косинусов,
cos a = (B 2 + C 2 — A 2 ) / (2BC)
= (60 2 + 30 2 — 50 2 ) / (2 · 2 2 — 50 2 ) / (2 60 · 30)
= (3600 + 900 – 2500) / 3600
= 2000 / 3600
cos A = 5/9.
Задача 4. Если cos A = 4/5, cos B = 12/13, найдите значение cos (A+B)?
Решение:
Здесь дано cos A = 4/5, cos B = 12/13
, поскольку A и B оба лежат в 4-м квадранте, а в 4-м квадранте Sin A и Sin B будут отрицательными.

Следовательно,
sin a = — √ (1 — cos 2 a)
= √ {1 — (4/5) 2 }
= — √ (1 — 16/25)
= -3/5
sin b =-√ (1-cos 2 B)
=-√ {1-(12/13) 2 }
= -5/13
Теперь
По формулам
cos(A + B) = cos (A) cos(B) – sin (A) sin (B)
= 4/5 × 12/13 – (-3/5)( -5/13)
= 48.
Solution:
Given that
LHS = cos4x
= cos2(2x)
= cos 2x {cos 2x = 1 – 2 sin 2 (x)}
= 1 – 2 sin 2 2(x)
= 1 – 2 (sin2x) 2
= 1- 2 (2SINX COSX) 2
= 1- 8SIN 2 XCOS 2 X
= RHS
HENCE PRED. Формулы угла, полуугла и приведения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19003
- OpenStax
- OpenStax
Развитие навыков
- Используйте формулы двойного угла, чтобы найти точные значения.

- Используйте формулы двойного угла для проверки тождества.
- Используйте формулы сокращения для упрощения выражения.
- Используйте формулы половинного угла, чтобы найти точные значения.
Велосипедные рампы, сделанные для соревнований (см. рисунок (PageIndex{1})) должны различаться по высоте в зависимости от уровня навыков участников. Для продвинутых участников угол, образованный рампой и землей, должен быть (theta) таким, что (tan theta=dfrac{5}{3}). Угол делится пополам для новичков. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Рисунок (PageIndex{1}): Велосипедные рампы для опытных гонщиков имеют более крутой наклон, чем для новичков.
Использование формул двойного угла для нахождения точных значений
В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций.
Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где (alpha=beta). Вывод формулы двойного угла для синуса начинается с формулы суммы
[sin(alpha+beta)=sin alpha cos beta+cos alpha sin beta. nonumber]
Если мы позволим (alpha=beta=theta), то получим
[begin{align*} sin(theta+theta)&= sin theta потому что тета+кос тета sin тета\ sin(2тета)&= 2sin тета cos тета. end{align*}]
Существует три варианта формулы двойного угла для косинуса. Во-первых, исходя из формулы суммы (cos(alpha+beta)=cos alpha cos beta−sin alpha sin beta), и пусть (alpha=beta= тета), у нас есть 92theta} end{align*}]
Как: Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение
- Нарисуйте треугольник, чтобы отражать предоставленную информацию.
- Определите правильную формулу двойного угла.

- Подставьте значения в формулу на основе треугольника.
- Упростить.
Пример (PageIndex{1}): использование формулы двойного угла для нахождения точного значения, включающего тангенс
Учитывая, что (tan theta=−dfrac{3}{4}) и (theta) находится в квадранте II, найдите следующее:
- (sin(2theta) )
- (cos(2тета))
- (загар(2тета))
Решение
Если мы нарисуем треугольник, отражающий предоставленную информацию, мы сможем найти значения, необходимые для решения задач на изображении. Нам даны (tan theta=−dfrac{3}{4}), такие что (theta) находится в квадранте II. Тангенс угла равен противолежащей стороне относительно прилежащей стороны, а поскольку (theta) находится во втором квадранте, прилежащая сторона находится на 92\ c&= 5 end{align*}]
Теперь мы можем нарисовать треугольник, подобный показанному на рисунке (PageIndex{2}).

Рисунок (PageIndex{2})
- Начнем с написания формулы двойного угла для синуса.
(sin(2theta)=2 sin theta cos theta)
Мы видим, что нам нужно найти (sin theta) и (cos theta). На основании рисунка (PageIndex{2}) мы видим, что гипотенуза равна (5), поэтому (sin θ=35), (sin θ=35) и ( cos θ=−45). Подставьте эти значения в уравнение и упростите. 92}\
&= dfrac{-dfrac{3}{2}}{1-dfrac{9}{16}}\
&= -dfrac{3}{2}left( dfrac{16}{7}right)\
&= -dfrac{24}{7}
end{align*}]Упражнение (PageIndex{1})
Учитывая (sin alpha=dfrac{5}{8}),с (theta) в квадранте I, найдите (cos(2 альфа)).
- Ответить
(cos(2alpha)=dfrac{7}{32})
Пример (PageIndex{2}): использование формулы двойного угла для косинуса без точных значений 92 3x end{выравнивание*}]
Анализ
Этот пример показывает, что мы можем использовать формулу двойного угла без точных значений.
Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.
Использование формул двойного угла для проверки идентичности
Установление идентичности с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для получения формул суммы и разности. Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной. 92 theta}{tan theta}}\ &= dfrac{2}{cot theta-tan theta} qquad text {Используйте взаимное тождество для } dfrac{1}{tan тета} end{выравнивание*}]
Анализ
Вот случай, когда более сложная часть исходного уравнения оказалась справа, но мы решили работать с левой частью. Однако, если бы мы выбрали для перезаписи левую часть, мы бы работали в обратном направлении, чтобы получить эквивалентность. Например, предположим, что мы хотели показать
92 тета)
Использование формул приведения для упрощения выражения
Формулы двойного угла можно использовать для получения формул приведения, которые являются формулами, которые мы можем использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса.
3(2x)=left[ dfrac{ 1}{2} sin(2x) right] [ 1−cos(4x) ) 92 x\[5pt] &= dfrac{10}{4}+dfrac{10}{2} cos(2x)+dfrac{10}{8}+dfrac{10}{8} cos(4x)\[5pt] &= dfrac{30}{8}+5cos(2x)+dfrac{10}{8}cos(4x)\[5pt] &= dfrac{ 15}{4}+5cos(2x)+dfrac{5}{4}cos(4x) end{align*}]
Использование формул половинного угла для нахождения точных значений
Следующий набор тождеств — это набор формул половинного угла , которые могут быть получены из формул приведения, и мы можем использовать их, когда имеем угол, равный половине размера особого угла. Если мы заменим (theta) на (dfrac{alpha}{2}), формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для (sinleft(dfrac{ alpha}{2}right)). Обратите внимание, что формулам половинного угла предшествует знак (pm) . Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается (dfrac{alpha}{2}) .
92left(dfrac{alpha}{2}right)&= dfrac{1-cosleft(2cdot dfrac{alpha}{2}right)}{1+cos влево (2 cdot dfrac { alpha} {2} right)} \ tan left ( dfrac { alpha} {2} right) & = pm sqrt { dfrac {1- cos alpha}{1+cos alpha}} end{align*}]
ФОРМУЛЫ ПОЛУУГЛОВ
Формулы для полууглов следующие:
[begin{align} sinleft(dfrac{alpha}{2}right)&=pm sqrt{dfrac{1-cosalpha}{2}} label{halfsine} \[5pt] cos влево ( dfrac { alpha} {2} right) & = pm sqrt { dfrac {1+ cos alpha} {2}} \ [5pt] tan left ( dfrac { alpha {2}right) &=pm sqrt{dfrac{1-cosalpha}{1+cosalpha}} =dfrac{sinalpha}{1+cosalpha} =dfrac{1-cosalpha}{sinalpha}end{align}] 9{circ}}{2}}\
&= sqrt{dfrac{1-dfrac{sqrt{3}}{2}}{2}}\
&= sqrt{dfrac{ dfrac{2-sqrt{3}}{2}}{2}}\
&= sqrt{dfrac{2-sqrt{3}}{4}}\
&= dfrac{ sqrt{2-sqrt{3}}}{2}
end{align*}]Помните, что мы можем проверить ответ с помощью графического калькулятора.

Анализ
Обратите внимание, что мы использовали только положительный корень, потому что (sin(15°)) положительно.
Howto: Зная тангенс угла и квадрант, в котором находится угол, найдите точные значения тригонометрических функций половины угла.
- Нарисуйте треугольник для представления данной информации.
- Определите правильную формулу половинного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Пример (PageIndex{8}): поиск точных значений с использованием тождеств половинного угла III, найдите точное значение следующего:
- (sinleft(dfrac{alpha}{2}right))
- (cosвлево(dfrac{alpha}{2}вправо))
- (tanleft(dfrac{alpha}{2}right))
Решение
Используя данную информацию, мы можем нарисовать треугольник, показанный на рисунке (PageIndex{3}).
Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить {17}).
Рисунок (PageIndex{3})
- Прежде чем мы начнем, мы должны помнить, что если (α) находится в квадранте III, то (180°<alpha<270°),so (dfrac{180°}{2}<dfrac {альфа}{2}<dfrac{270°}{2}). Это означает, что конечная сторона (dfrac{alpha}{2}) находится в квадранте II, так как (90°<dfrac{alpha}{2}<135°). Чтобы найти (sin dfrac{alpha}{2}), начнем с записи формулы половинного угла для синуса. Затем мы подставляем значение косинуса, которое мы нашли из треугольника на рисунке (PageIndex{3}), и упрощаем. [begin{align*} sin dfrac{alpha}{2}&= pm sqrt{dfrac{1-cos alpha}{2}}\ &= pm sqrt{ dfrac{1-(-dfrac{15}{17})}{2}}\ &= pm sqrt{dfrac{dfrac{32}{17}}{2}}\ &= pm sqrt{dfrac{32}{17}cdot dfrac{1}{2}}\ &= pm sqrt{dfrac{16}{17}}\ &= pm dfrac{ 4}{sqrt{17}}\ &= dfrac{4sqrt{17}}{17} end{align*}] Мы выбираем положительное значение (sin dfrac{alpha} {2}) поскольку угол оканчивается в квадранте II, а синус положителен в квадранте II.

- Чтобы найти (cos dfrac{alpha}{2}), мы напишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника на рисунке (PageIndex{3} ) и упростить. [ begin{align*} cos dfrac{alpha}{2}&= pm sqrt{dfrac{1+cos alpha}{2}}\ &= pm sqrt{ dfrac {1+left(-dfrac{15}{17}right)}{2}}\ &= pm sqrt{dfrac{dfrac{2}{17}}{2}} &= pm sqrt{dfrac{2}{17}cdot dfrac{1}{2}}\ &= pm sqrt{dfrac{1}{17}}\ &= — dfrac{sqrt{17}}{17} end{align*}] Мы выбираем отрицательное значение (cos dfrac{alpha}{2}) , потому что угол находится в квадранте II, потому что косинус отрицательно во II квадранте.
- Чтобы найти (tan dfrac{alpha}{2}), запишем формулу половинного угла для тангенса. Снова подставляем значение косинуса, которое мы нашли из треугольника на рисунке (PageIndex{3}), и упрощаем. [begin{align*} tan dfrac{alpha}{2}&= pm sqrt{dfrac{1-cos alpha}{1+cos alpha}}\ &= pm sqrt{dfrac{1-left(-dfrac{15}{17}right)}{1+left(-dfrac{15}{17}right)}}\ &= pm sqrt{dfrac{dfrac{32}{17}}{dfrac{2}{17}}}\ &= pm sqrt{dfrac{32}{2}}\ &= — sqrt{16}\ &= -4 end{align*}] Мы выбираем отрицательное значение (tan dfrac{alpha}{2}) потому что (dfrac{alpha}{ 2}) лежит в квадранте II, а тангенс отрицателен в квадранте II.

Упражнение (PageIndex{5})
Учитывая, что (sin alpha=-dfrac{4}{5}) и (alpha) лежит в квадранте IV, найдите точное значение (cos влево(dfrac{alpha}{2}вправо)).
- Ответить
(-dfrac{2}{sqrt{5}})
Пример (PageIndex{9}): нахождение измерения половинного угла
Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа сконструирована для соревнований высокого уровня с углом (θ) , образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если (tan θ=53) для соревнований более высокого уровня, каково измерение угла для соревнований новичков? 92&=34\ c&=sqrt{34} end{align*}]
Рисунок (PageIndex{4})
Мы видим, что (cos theta= dfrac{3}{sqrt{34}}=dfrac{3sqrt{34}}{34}). Мы можем использовать формулу половинного угла для тангенса: Поскольку (tan theta) находится в первом квадранте, то и (tan dfrac{theta}{2}).

[begin{align*}
tan dfrac{theta}{2}&= sqrt{dfrac{1-dfrac{3sqrt{34}}{34}}{1+ dfrac{3sqrt{34}}{34}}}\ 9{−1}(0,57)≈29,7°). Таким образом, угол рампы для соревнований новичков равен (≈29,7°).Media
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с формулами двойного угла, половинного угла и сокращения.
- Двухугольные удостоверения
- Полуугольные тождества
Ключевые уравнения
92 тета=dfrac{1−cos(2theta)}{1+cos(2theta)})
Формулы двойного угла
Формулы половинного угла
(sin dfrac{alpha}{2}=pm sqrt{dfrac{1−cos alpha}{2}})
(cos dfrac{alpha}{2}=pm sqrt{dfrac{1+cos alpha}{2}})
(tan dfrac{alpha}{2}=pm sqrt{dfrac{1−cos alpha}{1+cos alpha}})
(=dfrac{sin alpha}{1+cos alpha})
(=dfrac{1−cos alpha}{sin alpha})
Ключевые понятия
- Тождества двойных углов получаются из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса.
См. Пример (PageIndex{1}), Пример (PageIndex{2}), Пример (PageIndex{3}) и Пример (PageIndex{4}).
- Формулы редукции особенно полезны в математических вычислениях, поскольку они позволяют уменьшить мощность тригонометрического члена. См. Пример (PageIndex{5}) и Пример (PageIndex{6}).
- Формулы половинного угла позволяют нам найти значение тригонометрических функций, содержащих половинные углы, независимо от того, известен исходный угол или нет. См. Пример (PageIndex{7}), Пример (PageIndex{8}) и Пример (PageIndex{9}).
Авторы
Эта страница под названием 7.3: Формулы двойного угла, половинного угла и сокращения распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- расчетный график: да
- формулы двойного угла
- формула половинного угла
- формулы половинного угла
- Теорема Пифагора
- формулы приведения
- источник@https://openstax.
org/details/books/precalculus
Правило косинуса — математика GCSE
Введение
Что такое правило косинусов?
Как я могу использовать правило косинусов?
Как найти недостающую сторону или угол треугольника по правилу косинусов
Рабочий лист правила косинуса
Распространенные заблуждения
Похожие уроки
Практикуйте вопросы по правилу косинусов
Экзаменационные вопросы по правилу косинусов GCSE
Вы знали?
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Еженедельные онлайн-уроки повторения математики GCSE теперь доступны
Узнать больше
Введение
Что такое правило косинусов?
Как я могу использовать правило косинусов?
Как найти недостающую сторону или угол треугольника по теореме косинусов
Рабочий лист правила косинуса
Распространенные заблуждения
Похожие уроки
Практикуйте вопросы по правилу косинусов
Правило косинуса экзаменационные вопросы GCSE
Вы знали?
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о правиле косинуса, в том числе о том, как использовать правило косинуса для нахождения недостающих сторон и углов в непрямоугольных треугольниках и когда использовать правило косинуса вместо использования правила синусов, теоремы Пифагора или SOHCAHTOA.

Существуют также листы правил косинуса, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое правило косинусов?
правило косинусов (или закон косинусов) — это формула, которую можно использовать для вычисления недостающих сторон треугольника или для нахождения недостающего угла. Для этого нам нужно знать две схемы формулы и то, что представляет каждая переменная.
Посмотрите на треугольник ABC ниже.Этот треугольник устроен точно так же, как правило синусов, со сторонами, обозначенными строчными буквами, и противоположными углами, обозначенными теми же заглавными буквами, например. сторона b противоположна углу B. 9{2}-2bccos(A)\]
Что такое правило косинусов
Как я могу использовать правило косинусов?
Мы можем использовать правило косинусов, чтобы найти недостающие стороны и недостающие углы в треугольниках.

- Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.
Чтобы использовать правило косинусов, нам нужно рассмотреть угол, лежащий между двумя известными сторонами.
Взгляните на диаграмму,
Здесь угол A лежит между сторонами b и c (что-то вроде углового бутерброда).
Мы всегда обозначаем угол, который будем использовать, как A, тогда не имеет значения, как вы обозначите другие вершины (углы). Угол B и угол C могут быть любой вершиной, причем стороны b и стороны c являются их противоположными сторонами.
2 Укажите теорему косинусов, затем подставьте данные значения в формулу.
Теперь, когда мы знаем, какие стороны и углы у нас есть, нам нужно подставить эту информацию в правило косинусов.
Затем мы можем решить это уравнение, чтобы найти недостающую сторону или угол. 92}{2bc}Одно уравнение является перестановкой другого.
3 Решите уравнение .

Как только все подставлено в уравнение косинусов, мы можем решить уравнение для вычисления неизвестной стороны или угла.
Как найти недостающую сторону или угол треугольника, используя правило косинуса
Чтобы найти недостающую сторону или угол треугольника, используя правило косинуса:
- Обозначьте каждый угол (A, B, C) и каждая сторона (a, b, c) треугольника.
- Укажите теорему косинусов, затем подставьте данные значения в формулу.
- Решите уравнение.
Объясните, как найти недостающую сторону или угол треугольника с помощью теоремы косинусов
Рабочий лист по правилу косинуса
Получите бесплатный рабочий лист по правилу косинуса, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Икс
Рабочий лист правила косинуса
Получите бесплатный рабочий лист по правилу косинусов, содержащий более 20 вопросов и ответов.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры правила косинуса (недостающая сторона)
Пример 1: найдите недостающую сторону, используя правило косинуса
Найдите значение x для треугольника ABC, исправьте до 2 знаков после запятой.
- Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.
Вершины уже помечены буквой A, расположенной на используемом нами угле, поэтому нам нужно только пометить противоположные стороны a, b и c. 9{2}&=14,38516072…\
\x&=sqrt{14.38516072…}\
\x&=3,79mathrm{см}quad(2dp)\
end{aligned}Пример 2: найти недостающую сторону по теореме косинусов
Найти длину PQ для треугольника PQR, исправить до 3-х значащих цифр.
Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.
Здесь нам важно обозначить угол, который нам нужно использовать в первую очередь.
Для ответа на этот вопрос нам нужно найти сторону длины x, противоположную углу R. 9{2}&=110619,7432…\
\x&=sqrt{110619.7432…}\
\x&=333mathrm{m}quad(3sf)\
end{aligned}Пример 3: найдите недостающую сторону, используя правило косинуса
Найдите длину z для треугольника XYZ. Запишите свой ответ с подходящей степенью точности.
Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.
Чтобы найти длину z, нам нужно знать противоположный угол при Z. Поскольку мы знаем два других угла, 180 − (79{2}&=0,253939877…\
\z&=sqrt{0.253939877…}\
\z&=0,504mathrm{мм}quad(3dp)\
end{align}Примеры правила косинуса (недостающий угол)
Пример 4: найти недостающий угол, используя правило косинуса
Найдите величину угла θ для равнобедренного треугольника ABC. Запишите свой ответ с двумя значащими цифрами.
Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.

Здесь вершины уже помечены, и угол, который нам нужно найти, уже равен A, поэтому нам просто нужно заполнить противоположные стороны a, b и c. 9{ circ} четырехъядерный (2sf) \
end{aligned}Пример 5: найти недостающий угол по теореме косинусов
Найти величину угла θ для треугольника EFG. Напишите свой ответ с тремя значащими цифрами.
Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.
Здесь нам нужно пометить каждую вершину и угол. Поскольку нам нужно знать угол при F, он будет помечен как A, а противоположная сторона помечена как a. Остальные вершины помечены как B и C (неважно какие), а их противоположные стороны b и c указаны ниже. 9{ circ} четырехъядерный (3sf) \
end{aligned}Пример 6: найдите недостающий тупой угол, используя правило косинусов
Найдите величину угла θ для треугольника XYZ. Запишите свой ответ с точностью до 2 знаков после запятой.

Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.
Здесь нам нужно пометить каждую вершину и угол. Поскольку нам нужно знать угол при Z, он будет помечен как A, а противоположная сторона помечена как a. Остальные вершины обозначены как B и C, а их противоположные стороны b и c соответственно. 9{ circ} четырехъядерный (2dp) \
end{align}Распространенные заблуждения
- Теорема Пифагора и тригонометрия
Распространенной ошибкой является использование теоремы Пифагора вместо тригонометрии для нахождения недостающей стороны непрямого угла
3 9003 9003 Функция синуса вместо функции косинуса
Распространенной ошибкой является использование функции синуса вместо функции косинуса
- Неправильная маркировка вершин и сторон
«А» — угол между двумя сторонами b и c.
Обычно вместо угла А используется один из углов треугольника, поэтому расчет будет неверным.
- неправильно, используя правило косинуса в качестве 2 = B 2 + C 2 + 2BCCOS (A)
Здесь 2BCCOS (A) добавлено к B 2 + C , 2BCCOS (A) добавлено к B 2 + C . 2 . Это очень распространенное заблуждение, которого легко избежать.
- Подстановка ошибок
Распространенной ошибкой является неправильная подстановка в правило косинуса с использованием длины стороны ‘a’ вместо угла A
- Подстановка значений без правильного применения правила косинуса BIDMAS
При вычислении правила косинусов важно соблюдать порядок операций.
- Есть ли неоднозначный случай для правила косинуса, как для правила синусов?
Простой ответ — нет из-за природы функции косинуса и связи с нахождением угла внутри треугольника.
Например.
Если вы возьмете cos(60), это вернет тот же ответ на калькуляторе, что и cos(300).Сумма углов треугольника должна составлять 180º, поэтому ни один из углов не будет больше 180º. Важно помнить, что арккосинус любого числа от 0 до -1 вернет тупой угол. Дополнительные сведения см. в разделе Тригонометрические графики.
Правило косинуса является частью нашей серии уроков по тригонометрии. Возможно, вам будет полезно начать с основного урока по тригонометрии, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения более подробной информации по отдельным темам. Другие уроки в этой серии включают:
- Тригонометрия
- SOHCATOA
- Правило синусов
- График Tan
- График Cos
- График Sin
- Тригонометрические функции
{ круг}
end{выровнено}(1)
2. Четырехугольник ABCD составлен из двух треугольников.

Найдите длину AD.
(5 баллов)
Показать ответ
tan(44)=frac{BD}{76}
(1)
begin{выровнено}
BD&=76 times tan(44)\\
BD&=73,39 mathrm{см}
end{выровнено}(1)
9{2}&=1066,228
end{выровнено}(1)
begin{выровнено}
a&=sqrt{1066.228}\\
а&=32,7mathrm{км}
end{выровнено}(1)
Знаете ли вы?
Правило косинуса получено из использования теоремы Пифагора c 2 = a 2 + b 2 и функции косинуса:
[ cos(theta)=frac{A}{ H}]
Для этого треугольник разбивается на два прямоугольных треугольника. Затем мы можем использовать теорему Пифагора, чтобы вычислить c 2 и 2 отдельно, а затем мы используем функцию косинуса для вычисления ширины одного из двух треугольников.

Примечание. Вы не обязаны знать, как вывести правило косинуса, однако для его вывода требуется только знание учебного плана GCSE, как и для вывода квадратичной формулы.
Контрольный список для обучения
Теперь вы научились:
- знать и применять правило косинусов для нахождения неизвестных длин и углов
Все еще застрял?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять или изменять ваши настройки файлов cookie. Принять
Калькулятор закона косинусов
Создано Богной Шик и Ханной Памула, докторантами
Отредактировано Джеком Боуотером
Последнее обновление: 03 сентября 2022 г.

Содержание:
- Что такое закон косинусов4 формула 9005 косинусов?
- Применение закона косинусов
- Доказательство закона косинусов
- Как пользоваться калькулятором закона косинусов
- Закон косинусов — пример SSS треугольных задач. Вы узнаете, что такое закон косинусов (также известный как правило косинусов), закон косинусов формула и ее приложения. Прокрутите вниз, чтобы узнать, когда и как использовать закон косинусов, и ознакомьтесь с доказательствами этого закона. Благодаря этому калькулятору треугольников вы сможете быстро найти свойства любого произвольного треугольника.
Но если вам почему-то интересно, что такое косинус, лучше взгляните на наш калькулятор косинуса.
Формула закона косинусов
Закон косинусов гласит, что для треугольника со сторонами и углами, обозначенными символами, как показано выше,
a² = b² + c² - 2bc * cos(α)
b² = a² + c² - 2ac * cos(β)
c² = a² + b² - 2ab * cos(γ)
8 Для прямоугольного треугольника угол гамма, который является углом между катетамиaиb, равен 90°.Косинус 90° = 0, поэтому в этом частном случае формула закона косинусов сводится к известному уравнению теоремы Пифагора:
a² = b² + c² - 2bc * cos(90°)
a² = b² + c²Что такое закон косинусов?
Закон косинусов (альтернативно формула косинуса или правило косинуса) описывает отношение между длинами сторон треугольника и косинусом его углов. Его можно применять ко всем треугольникам, а не только к прямоугольным. Этот закон обобщает теорему Пифагора, так как позволяет вычислить длину одной из сторон, зная длину обеих сторон и угол между ними.
Закон появился в Элементе Евклида, математическом трактате, содержащем определения, постулаты и геометрические теоремы. Евклид не сформулировал его так, как мы изучаем его сегодня, поскольку понятие косинуса еще не было разработано.
AB² = CA² + CB² - 2 * CA * CH(для острых углов, «+» для тупых)Однако мы можем легко переформулировать теорему Евклида в текущей форме формулы косинуса:
CH = CB * cos(γ), поэтомуAB² = CA² + CB² - 2 * CA * (CB * cos(γ))Меняя обозначения, получаем знакомое выражение:
c² = a² + b² - 2ab * cos(γ)первое явное уравнение косинуса было представлено персидским математиком д'Аль-Каши в 15 веке.
В 16 веке закон был популяризирован известным французским математиком Виете, прежде чем он получил свою окончательную форму в 19 веке.
Применение закона косинусов
Вы можете преобразовать эти формулы закона косинусов для решения некоторых задач триангуляции (решение треугольника). Вы можете использовать их, чтобы найти:
- Третья сторона треугольника , зная две стороны и угол между ними (SAS):
а = √[b² + c² - 2bc * cos(α)]b = √[a² + c² - 2ac * cos(β)]с = √[a² + b² - 2ab * cos(γ)]- Углы треугольника , зная все три стороны (SSS):
α = arccos [(b² + c² - a²)/(2bc)]β = arccos [(a² + c² - b²)/(2ac)]γ = arccos [(a² + b² - c²)/(2ab)]- Третья сторона треугольника , зная две стороны и угол, противолежащий одной из них (SSA):
а = b * cos(γ) ± √[c² - b² * sin²(γ)]b = c * cos(α) ± √[a² - c² * sin²(α)]c = a * cos(β) ± √[b² - a² * sin²(β)]Просто помните, что зная две стороны и прилежащий угол, можно получить два различных возможных треугольника (или одно или ноль положительных решений, в зависимости от заданных данных).
Вот почему мы решили реализовать в этом инструменте SAS и SSS, но не SSA.
Закон косинусов является одним из основных законов и широко используется во многих геометрических задачах. Мы также используем этот закон во многих Omnitools, если упомянуть лишь некоторые из них:
- калькулятор угла треугольника
- Калькулятор площади треугольника
- калькулятор периметра треугольника
- Калькулятор треугольной призмы
Также калькулятор закона косинусов можно совмещать с законом синусов для решения других задач, например, нахождения стороны треугольника по двум углам и одной стороне (AAS и ASA).
Доказательство закона косинусов
Есть много способов доказать уравнение уравнения косинусов. Вы уже читали об одном из них — он исходит непосредственно из формулировки закона Евклидом и применения теоремы Пифагора. Вы можете написать другие доказательства закона косинусов, используя:
1. Тригонометрия
Проведите линию для высоты треугольника и разделите перпендикулярную к ней сторону на две части:
b = b₁ + b₂
Из определения синуса и косинуса,b₁может быть выражено какa * cos(γ)иb₂ = c * cos(α).Отсюда:
b = a * cos(γ) + c * cos(α)и, умножив это наb, мы получим:
b² = ab * cos(γ) + bc * cos(α )(1)Аналогичные уравнения можно вывести для двух других сторон:
a² = ac * cos(β) + ab * cos(γ)(2)
c² = bc * cos(α) + ac * cos(β)(3)Чтобы закончить доказательство закона косинусов, нужно сложить уравнения (1) и (2) и вычесть (3):
a² + b² - c² = ac * cos(β) + ab * cos(γ) + bc * cos(α) + ab * cos(γ) - bc * cos(α) - ac * cos(β)
Сокращение и упрощение уравнения дают одну из форм теоремы косинусов: )Изменяя порядок их сложения и вычитания, можно вывести формулу другого закона косинуса.
2. Формула расстояния
Пусть
C = (0,0),A = (b,0), как на картинке.Чтобы найти координаты B, мы можем использовать определение синуса и косинуса:
B = (a * cos(γ), a * sin(γ))Из формулы расстояния мы можем найти что:
c = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(a * cos(γ) - b)² + (a * sin(γ) - 0)²]Таким образом:
c² = a² * cos(γ)² - 2ab * cos(γ) + b² + a² * sin(γ)²
c² = b² + a²(sin(γ)² + cos(γ)²) - 2ab * cos(γ)Поскольку сумма квадратов синуса и косинуса равна 1, получаем окончательную формулу:
3.
Теорема Птолемея
Предположим, у нас есть треугольник ABC, нарисованный по описанной окружности, как показано на рисунке.
Постройте конгруэнтный треугольник ADC, где AD = BC и DC = BA
Высоты из точек B и D делят основание AC на E и F соответственно. CE равно FA.
Из определения косинуса мы можем выразить CE как
a * cos(γ).Таким образом, мы можем написать, что
BD = EF = AC - 2 * CE = b - 2 * a * cos(γ).Тогда для нашего четырехугольника ADBC мы можем использовать теорему Птолемея , которая объясняет связь между четырьмя сторонами и двумя диагоналями. Теорема утверждает, что для вписанных четырехугольников сумма произведений противоположных сторон равна произведению двух диагоналей:
ВС * DA + CA * BD = AB * CD, в нашем случае:
.
a² + b * (b - 2 * a * cos(γ)) + a² = c²После сокращения получаем окончательную формулу:
c² = a² + b² - 2ab * cos(γ))Большим преимуществом этих трех доказательств является их универсальность — они работают для остроугольных, прямоугольных и тупоугольных треугольников.

- Использование закона синусов
- Использование определения скалярного произведения
- Сравнение площадей
- Геометрия круга
Последние два доказательства требуют различия между различными случаями треугольника. Доказательство, основанное на определении скалярного произведения, показано в другой статье, а доказательство с использованием закона синусов довольно сложное, поэтому мы решили не воспроизводить его здесь. Если вам интересно узнать об этих доказательствах закона косинусов, ознакомьтесь с объяснением в Википедии.
Как пользоваться калькулятором закона косинусов
Начните с формулирования проблемы. Например, вы можете знать две стороны треугольника и угол между ними и искать оставшуюся сторону.
Введите известные значения в соответствующие поля этого калькулятора треугольников.
Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.
Посмотрите, как наш калькулятор закона косинусов выполнит все расчеты за вас!
Закон косинусов — пример SSS
Если ваша задача состоит в том, чтобы найти углы треугольника по всем трем сторонам, все, что вам нужно сделать, это использовать преобразованные формулы правила косинуса:
α = arccos [(b² + c² - a²)/(2bc)]
β = arccos [(a² + c² - b²)/(2ac)]
γ = arccos [(a² + b² - c²)/(2ab)]Вычислим один из углов. Предположим, у нас есть a = 4 дюйма, b = 5 дюймов и c = 6 дюймов. Мы будем использовать первое уравнение, чтобы найти α:
α = arccos [(b² + c² - a²)/(2bc)]
= arccos [(5² + 6² - 4²)/(2 * 5 * 6)]
= arccos [( 25 + 36 - 16)/60]
= arccos [(45/60)] = arccos [0,75]
α = 41,41°Второй угол можно вычислить из второго уравнения аналогично, а третий угол можно найти, зная, что сумма углов треугольника равна 180° (π/2).

Если вы хотите сэкономить время, введите длины сторон в наш калькулятор закона синусов — наш инструмент — беспроигрышный вариант! Просто следуйте этим простым шагам:
- Выберите вариант в зависимости от заданных значений . Нам нужно подобрать второй вариант — SSS (3 стороны) .
- Введите известные значения . Введите стороны: a = 4 дюйма, b = 5 дюймов и c = 6 дюймов.
- Калькулятор показывает результат! В нашем случае углы равны α = 41,41°, β = 55,77° и γ = 82,82°.
После такого объяснения мы уверены, что вы поняли, что такое закон косинуса и когда его использовать. Попробуйте этот инструмент, выполните несколько упражнений и помните, что практика делает его постоянным!
Часто задаваемые вопросы
Когда следует использовать закон косинусов?
Используйте закон косинусов, если вам нужно вычислить:
- Сторона треугольника через две другие стороны и угол между ними.

- Три угла треугольника при данных его сторонах.
- Сторона треугольника, если даны две другие стороны и угол, противолежащий одной из этих сторон.
Когда следует использовать закон косинусов против теоремы Пифагора?
Закон косинусов является обобщением теоремы Пифагора, поэтому всякий раз, когда работает последняя, можно применять и первую. Но не наоборот!
Закон косинусов справедлив только для прямоугольных треугольников?
Нет , закон косинусов справедлив для всех треугольников. На самом деле, применяя закон косинусов к прямоугольному треугольнику, вы придёте к старой доброй теореме Пифагора.
Чему равна третья сторона треугольника со сторонами 5 и 6?
Кроме двух сторон нужно знать один из внутренних углов треугольника. Допустим, это угол γ = 30° между сторонами 5 и 6 . Тогда:
- Вспомните формулу закона косинусов c² = a² + b² — 2ab × cos(γ)
- Подставьте значения a = 5 , b = 6 , γ = 30° .

| tg(2α) = | 2tg(α)
1 – tg2(α) |
| ctg(2α) = | ctg2(α) – 1
2ctg(α) |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2021
Направляющие
косинусы вектора.
Направляющие
косинусы вектора a –
это косинусы углов, которые вектор
образует с положительными полуосями
координат.
Чтобы
найти направляющие косинусы вектора a
необходимо соответствующие координаты
вектора поделить на модуль вектора.
Свойство:
Сумма квадратов направляющих косинусов
равна единице.
Так
в случае
плоской задачи
направляющие косинусы вектора a = {ax; ay}
находятся по формулам:
;
Пример
вычисления направляющих косинусов
вектора:
Найти
направляющие косинусы вектора a = {3; 4}.
Решение:
|a| =
;
Так
в случае
пространственной задачи
направляющие косинусы вектора a
= {ax;
ay;
az}
находятся по формулам:


Пример
вычисления направляющих косинусов
вектора
Найти
направляющие косинусы вектора a
= {2; 4; 4}.
Решение:
|a|
=
;

|
§ |
|
Направление
Рис.
Из
Легко 1) 2) координаты |
“Как
найти направляющие косинусы вектора”
Обозначьте
через альфа, бета и гамма углы, образованные
вектором а с положительным направлением
координатных осей (см. рис.1). Косинусы
этих углов называются направляющими
косинусами вектора а.
1
Так
как координаты а
в декартовой прямоугольной системе
координат равны проекциям вектора на
координатные оси, то
а1 = |a|cos(альфа), a2
= |a|cos(бета), a3 = |a|cos(гамма). Отсюда:
cos
(альфа)=a1||a|, cos(бета) =a2||a|, cos(гамма)=
a3/|a|.
При
этом
|a|=sqrt(a1^2+ a2^2+ a3^2). Значит
cos
(альфа)=a1|sqrt(a1^2+
a2^2+ a3^2), cos(бета)
=a2|sqrt(a1^2+ a2^2+ a3^2),
cos(гамма)=
a3/sqrt(a1^2+ a2^2+ a3^2).
2
Следует
отметить основное свойство направляющих
косинусов. Сумма квадратов направляющих
косинусов вектора равна единице.
Действительно,
cos^2(альфа)+cos^2(бета)+cos^2(гамма)=
=
a1^2|(a1^2+ a2^2+ a3^2)+ a2^2|(a1^2+ a2^2+ a3^2)+ a3^2/(a1^2+ a2^2+
a3^2) =
=(a1^2+ a2^2+ a3^2)|(a1^2+ a2^2+ a3^2) = 1.
3
Первый
способ
Пример:
дано: вектор а={1, 3, 5). Найти его направляющие
косинусы.
Решение. В соответствии с
найденным выпишем:
|а|= sqrt(ax^2+ ay^2+
az^2)=sqrt(1+9 +25)=sqrt(35)=5,91.
Таким образом, ответ можно
записать в следующей форме:
{cos(альфа),
cos(бета), cos(гамма)}={1/sqrt(35), 3/sqrt (35),
5/(35)}={0,16;0,5;0,84}.
4
Второй
способ
При
нахождении направляющих косинусов
вектора а, можно использовать методику
определения косинусов углов с помощью
скалярного произведения. В данном случае
в виду имеются углы между
а и направляющими единичными векторами
прямоугольных декартовых координат i,
j и k. Их координаты {1, 0, 0}, {0, 1, 0}, {0, 0, 1},
соответственно.
Следует напомнить,
что скалярное произведение векторов
определяется так.
Если
угол между векторами ф, то скалярное
произведение двух ветров (по определению)
– это число, равное произведению модулей
векторов на cosф. (a, b) = |a||b|cos ф. Тогда, если
b=i, то (a, i) = |a||i|cos(альфа),
или a1 =
|a|cos(альфа). Далее все действия выполняются
аналогично способу 1, с учетом координат
j и k.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #








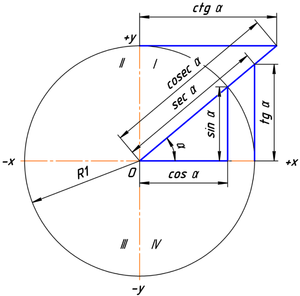













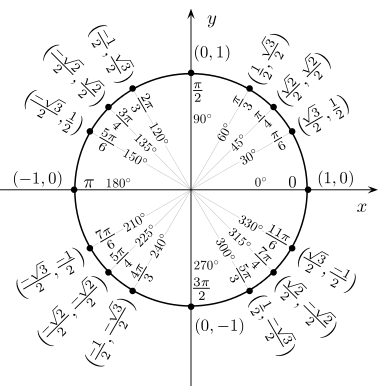







































![sin(nalpha)=sum_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}cos^{n-2k-1}alpha,sin^{2k+1}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb020e5dfc3b2d5dfe1d1a0c571487ce387a8153)
![cos(nalpha)=sum_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}cos^{n-2k}alpha,sin^{2k}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/84f285d7cb530e87d8a9e33cff84fd4a4c9a8205)
![mathrm{tg}(nalpha)=frac{sin(nalpha)}{cos(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{tg}^{2k+1}alpha}}{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{tg}^{2k}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/8800a20a70495802fc2de287bb98d155e14720b1)
![mathrm{ctg}(nalpha)=frac{cos(nalpha)}{sin(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{ctg}^{n-2k}alpha}}{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{ctg}^{n-2k-1}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/90744f04ee2a1e34b1f0763e310c1c1d071f240d)



























































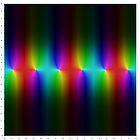


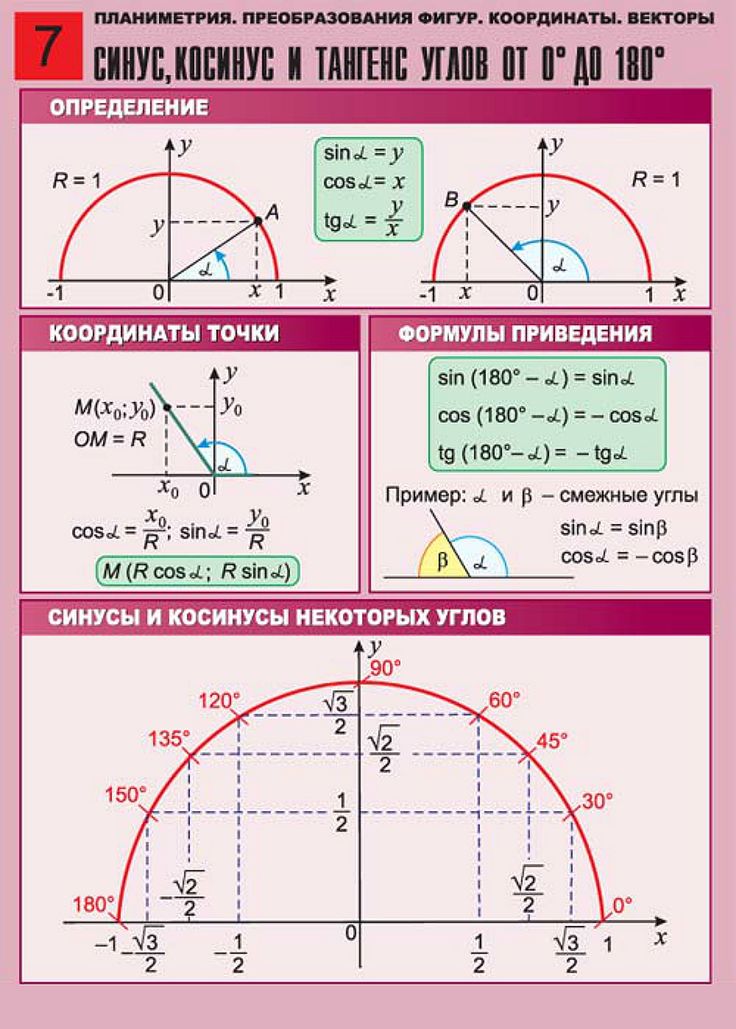

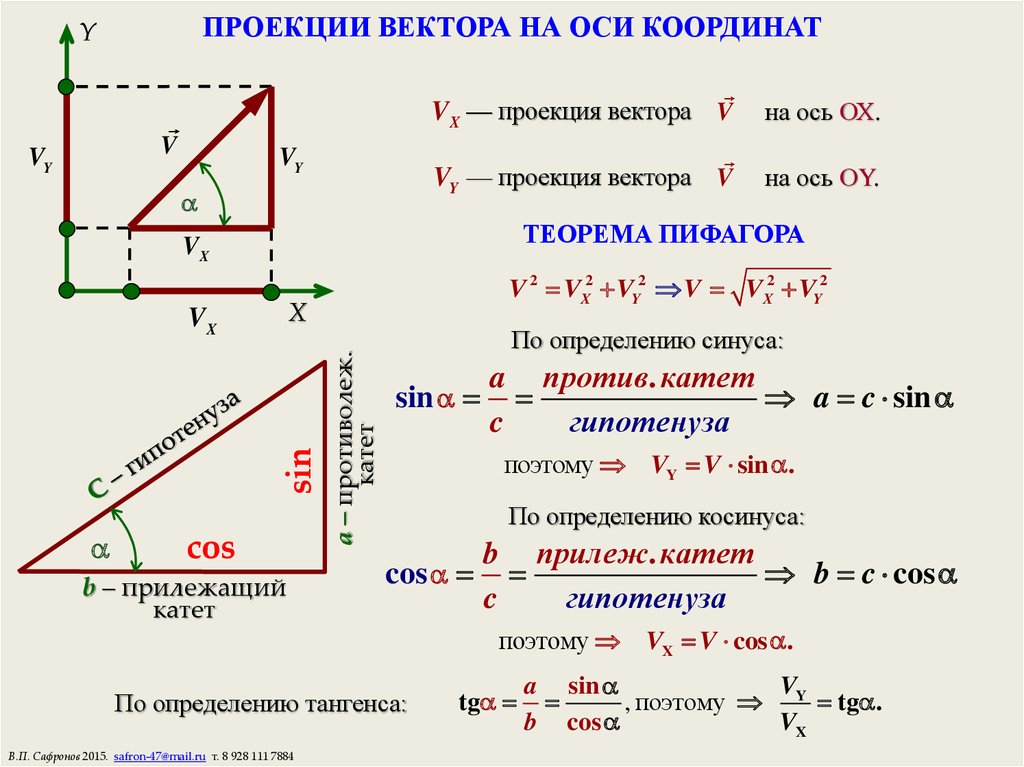 Для любого угла α верно утверждение:
Для любого угла α верно утверждение: Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как тангенс θ.
Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как тангенс θ. 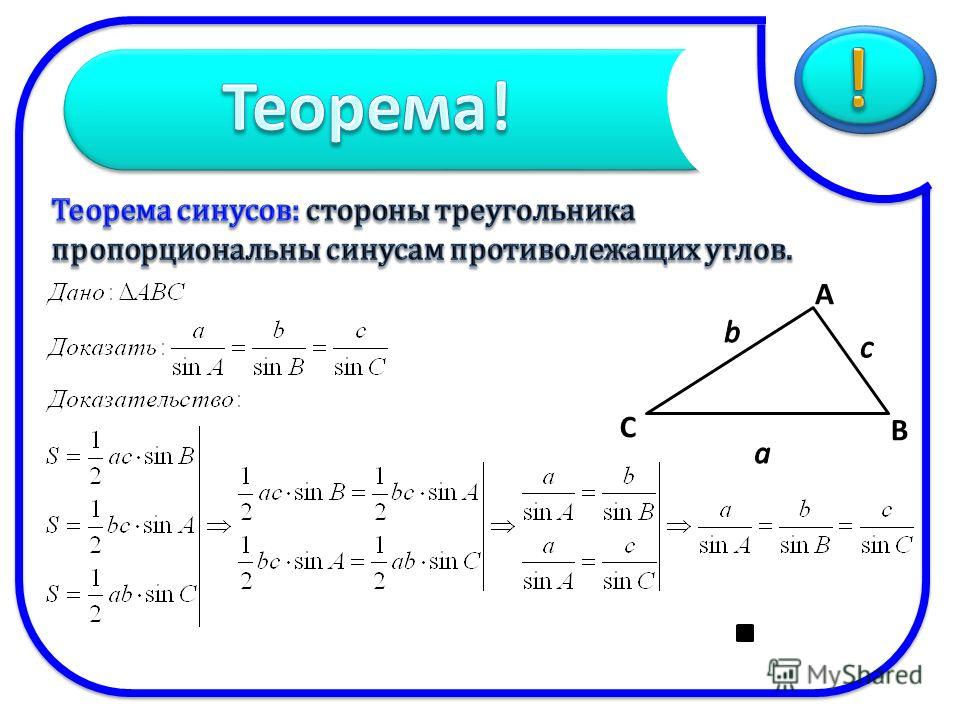


 Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где (alpha=beta). Вывод формулы двойного угла для синуса начинается с формулы суммы
Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где (alpha=beta). Вывод формулы двойного угла для синуса начинается с формулы суммы 
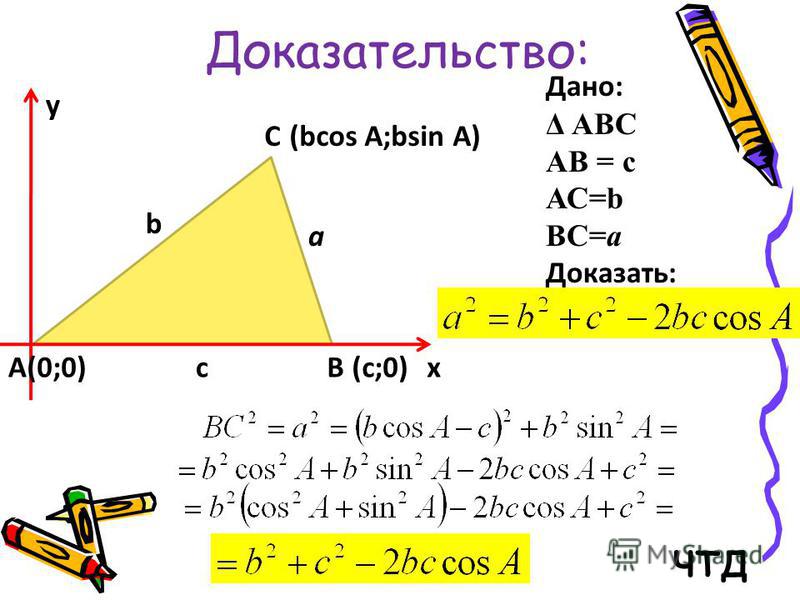
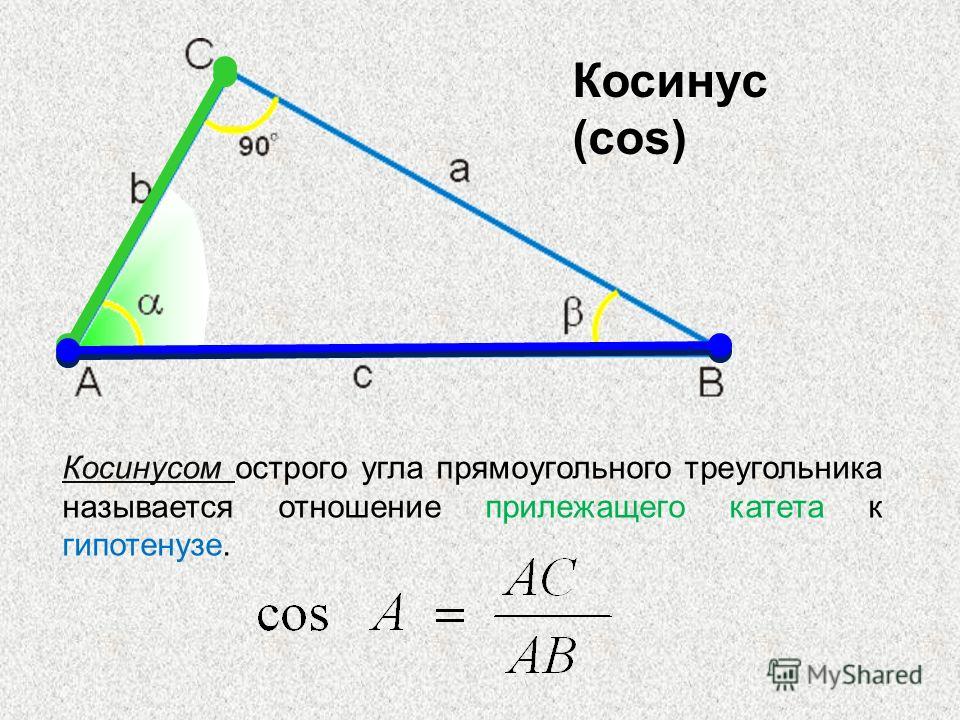 Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.
Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.  3(2x)=left[ dfrac{ 1}{2} sin(2x) right] [ 1−cos(4x) ) 92 x\[5pt] &= dfrac{10}{4}+dfrac{10}{2} cos(2x)+dfrac{10}{8}+dfrac{10}{8} cos(4x)\[5pt] &= dfrac{30}{8}+5cos(2x)+dfrac{10}{8}cos(4x)\[5pt] &= dfrac{ 15}{4}+5cos(2x)+dfrac{5}{4}cos(4x) end{align*}]
3(2x)=left[ dfrac{ 1}{2} sin(2x) right] [ 1−cos(4x) ) 92 x\[5pt] &= dfrac{10}{4}+dfrac{10}{2} cos(2x)+dfrac{10}{8}+dfrac{10}{8} cos(4x)\[5pt] &= dfrac{30}{8}+5cos(2x)+dfrac{10}{8}cos(4x)\[5pt] &= dfrac{ 15}{4}+5cos(2x)+dfrac{5}{4}cos(4x) end{align*}]  92left(dfrac{alpha}{2}right)&= dfrac{1-cosleft(2cdot dfrac{alpha}{2}right)}{1+cos влево (2 cdot dfrac { alpha} {2} right)} \ tan left ( dfrac { alpha} {2} right) & = pm sqrt { dfrac {1- cos alpha}{1+cos alpha}} end{align*}]
92left(dfrac{alpha}{2}right)&= dfrac{1-cosleft(2cdot dfrac{alpha}{2}right)}{1+cos влево (2 cdot dfrac { alpha} {2} right)} \ tan left ( dfrac { alpha} {2} right) & = pm sqrt { dfrac {1- cos alpha}{1+cos alpha}} end{align*}] 
 Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить {17}).
Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить {17}). 

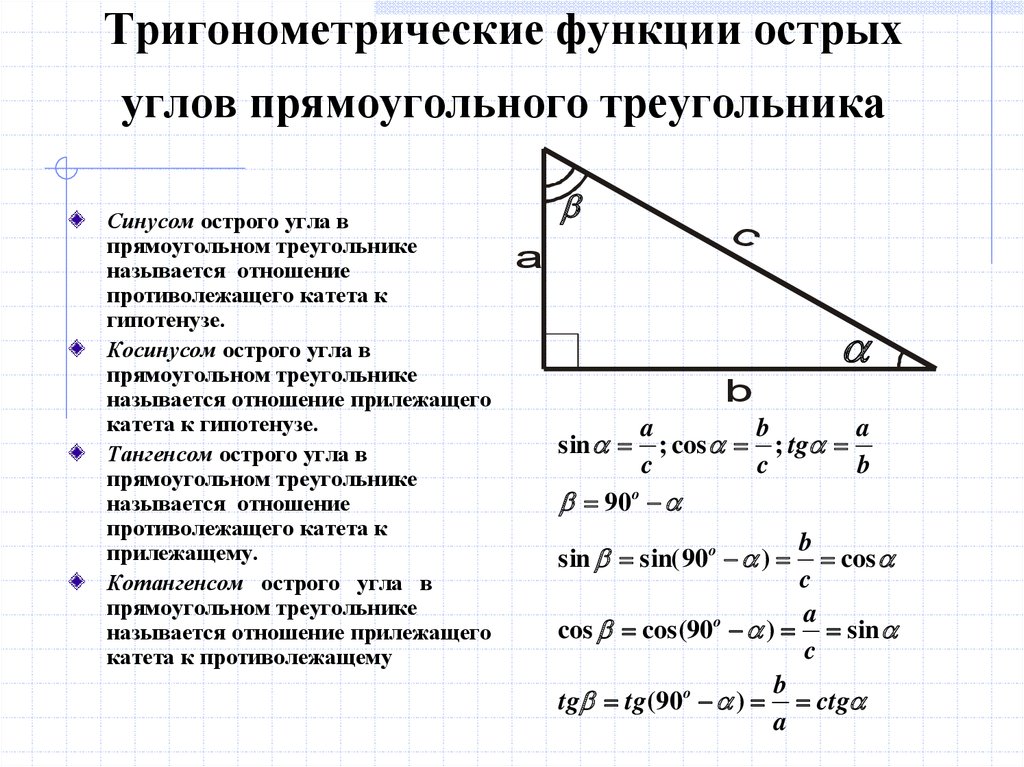
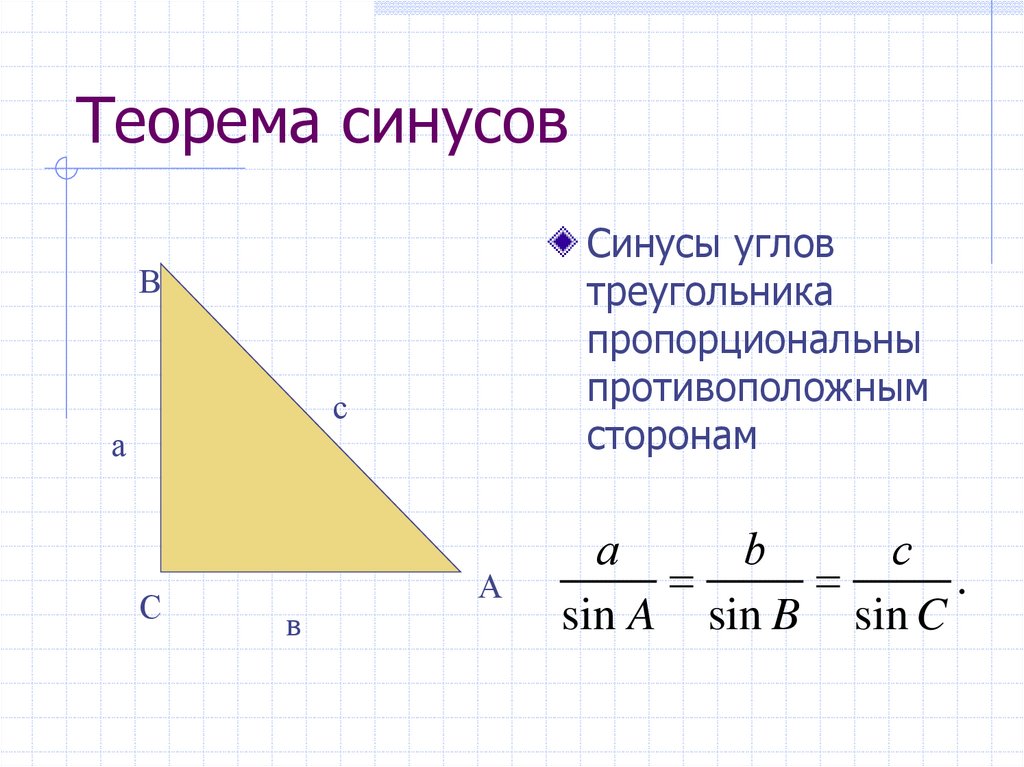 См. Пример (PageIndex{1}), Пример (PageIndex{2}), Пример (PageIndex{3}) и Пример (PageIndex{4}).
См. Пример (PageIndex{1}), Пример (PageIndex{2}), Пример (PageIndex{3}) и Пример (PageIndex{4}). 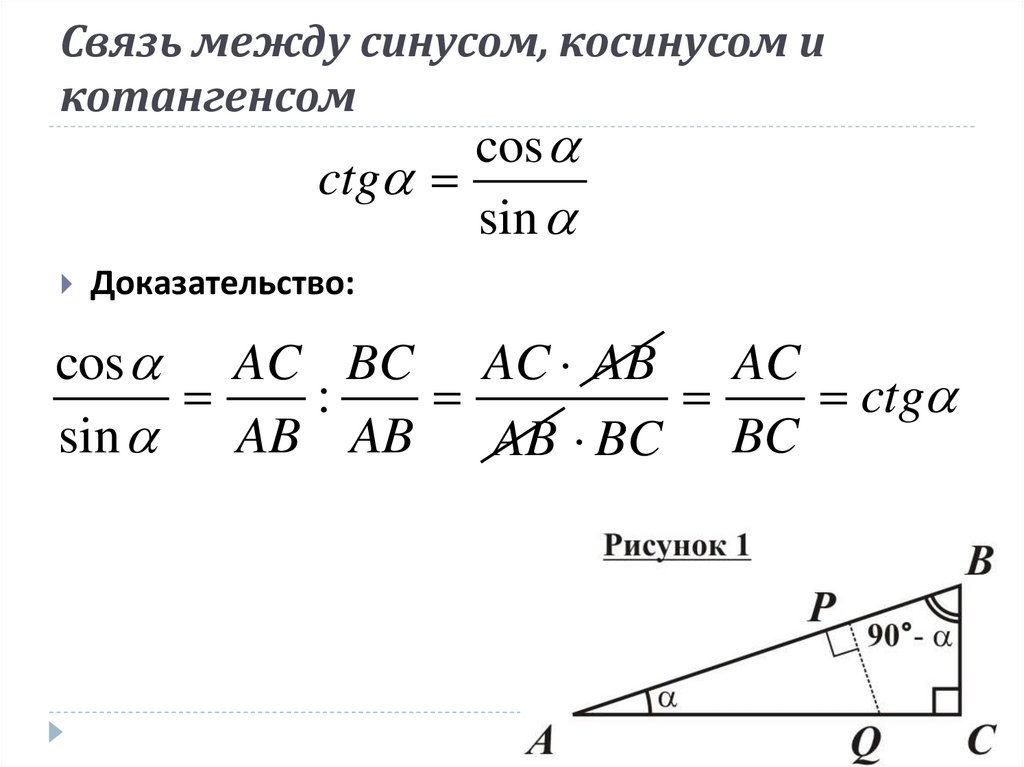 org/details/books/precalculus
org/details/books/precalculus 
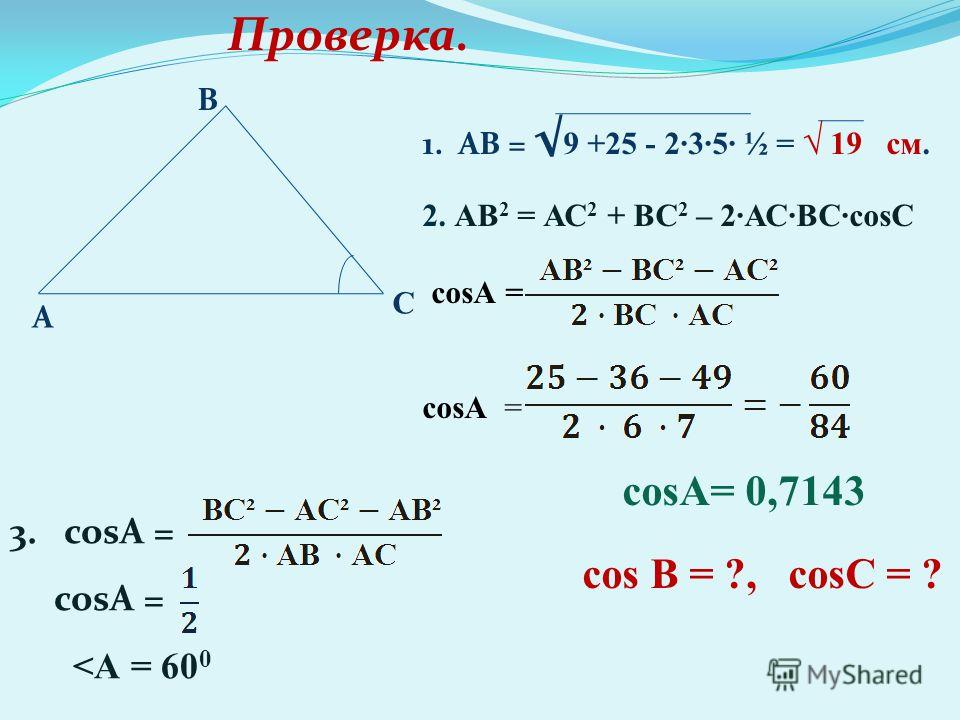
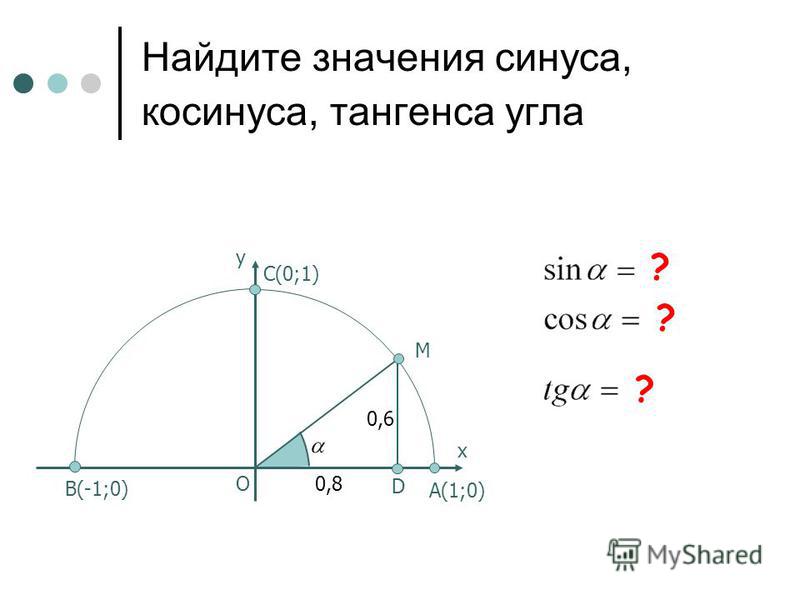
 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.  Для ответа на этот вопрос нам нужно найти сторону длины x, противоположную углу R. 9{2}&=110619,7432…\
Для ответа на этот вопрос нам нужно найти сторону длины x, противоположную углу R. 9{2}&=110619,7432…\

 Обычно вместо угла А используется один из углов треугольника, поэтому расчет будет неверным.
Обычно вместо угла А используется один из углов треугольника, поэтому расчет будет неверным. 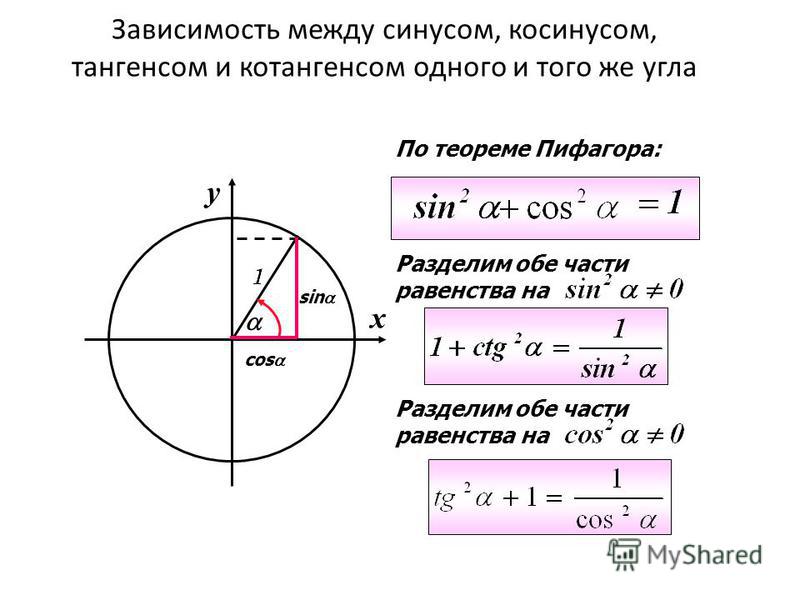 Например.
Например. 


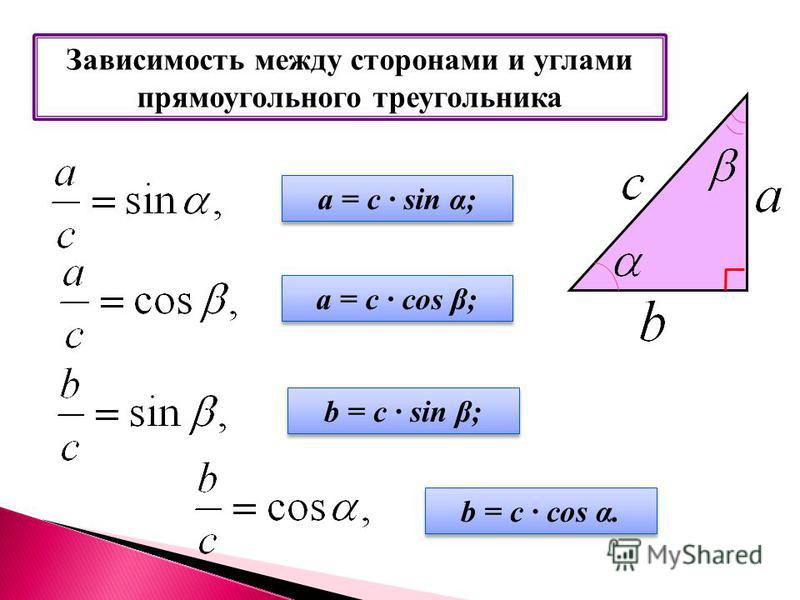 Косинус 90° = 0, поэтому в этом частном случае формула закона косинусов сводится к известному уравнению теоремы Пифагора:
Косинус 90° = 0, поэтому в этом частном случае формула закона косинусов сводится к известному уравнению теоремы Пифагора:  В 16 веке закон был популяризирован известным французским математиком Виете, прежде чем он получил свою окончательную форму в 19 веке.
В 16 веке закон был популяризирован известным французским математиком Виете, прежде чем он получил свою окончательную форму в 19 веке. 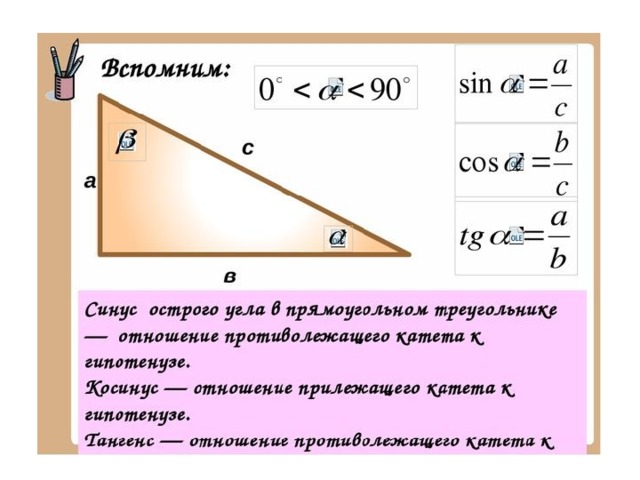 Вот почему мы решили реализовать в этом инструменте SAS и SSS, но не SSA.
Вот почему мы решили реализовать в этом инструменте SAS и SSS, но не SSA.  Отсюда:
Отсюда:  Теорема Птолемея
Теорема Птолемея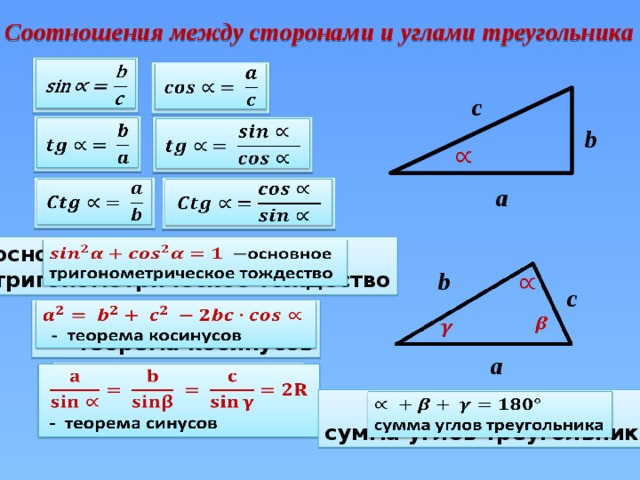
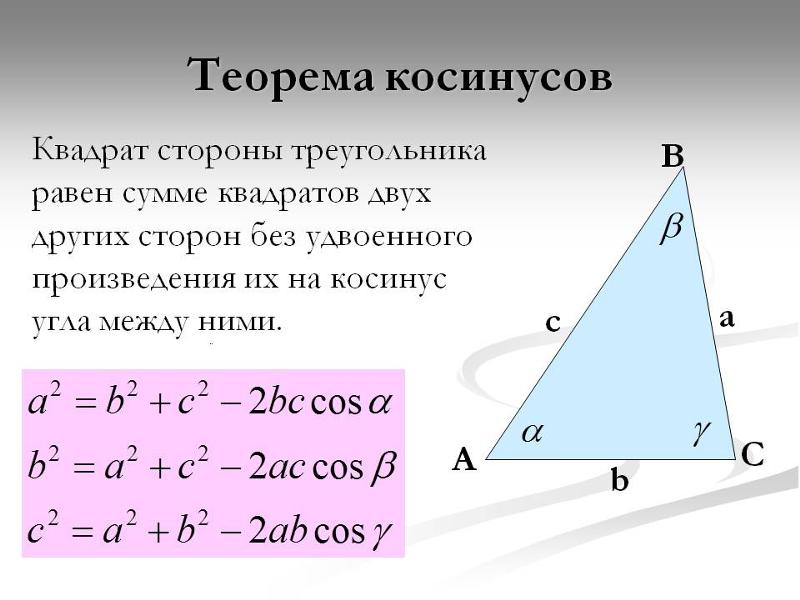 Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.
Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.