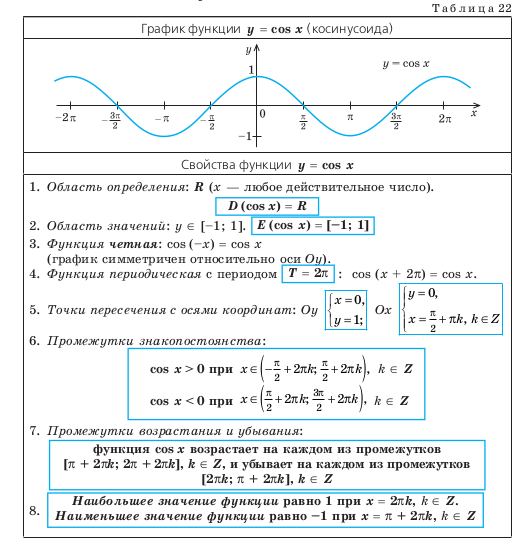
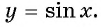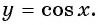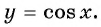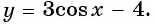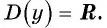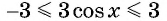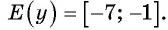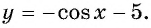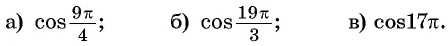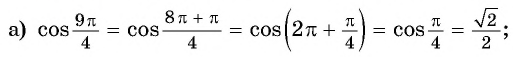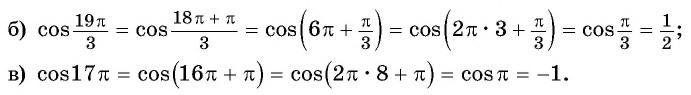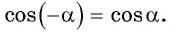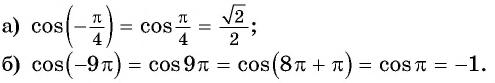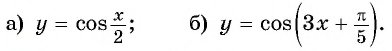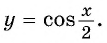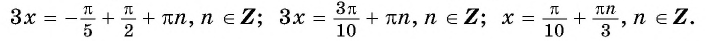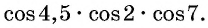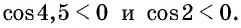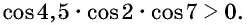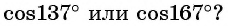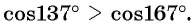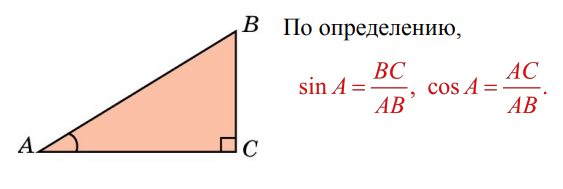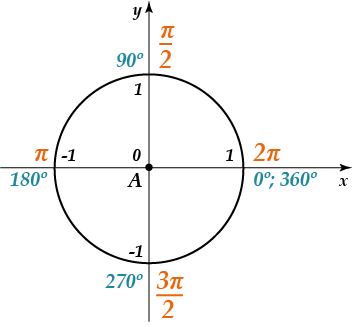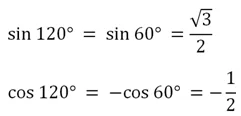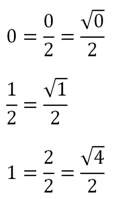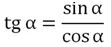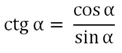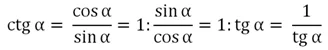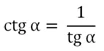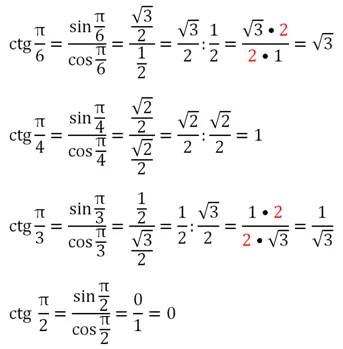- Развертка абсциссы движения точки по числовой окружности в функцию от угла
- Свойства функции y=cosx
- Примеры
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
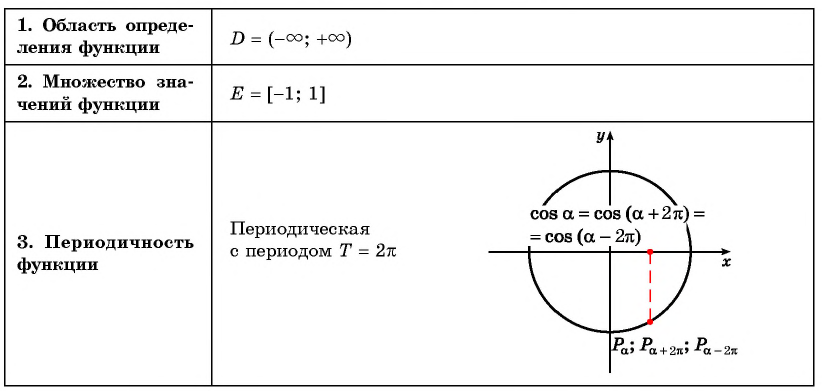
Развертка абсциссы движения точки по числовой окружности в функцию от угла (см. §2 данного справочника).
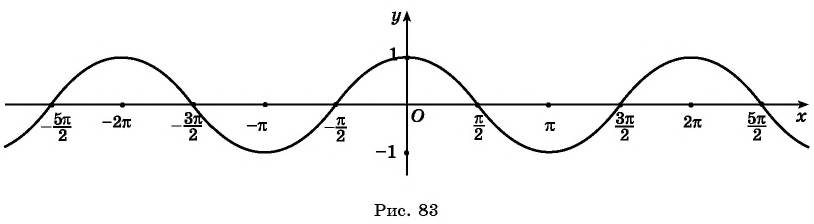
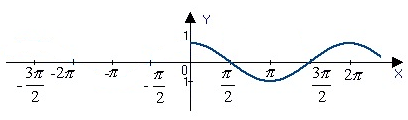
Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
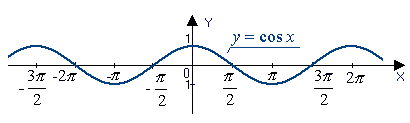
В результате получаем график y=cosx для любого (xinmathbb{R}).
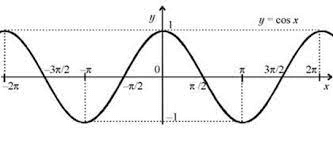
График y=cosx называют косинусоидой.
Часть косинусоиды для –π≤x≤π называют волной косинусоиды.
Часть косинусоиды для (-fracpi2leq xleqfracpi2) называют полуволной или аркой косинусоиды.
Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».
п.2. Свойства функции y=cosx
1. Область определения (xinmathbb{R}) – множество действительных чисел.
2. Функция ограничена сверху и снизу $$ -1leq cosxleq 1 $$ Область значений (yin[-1;1])
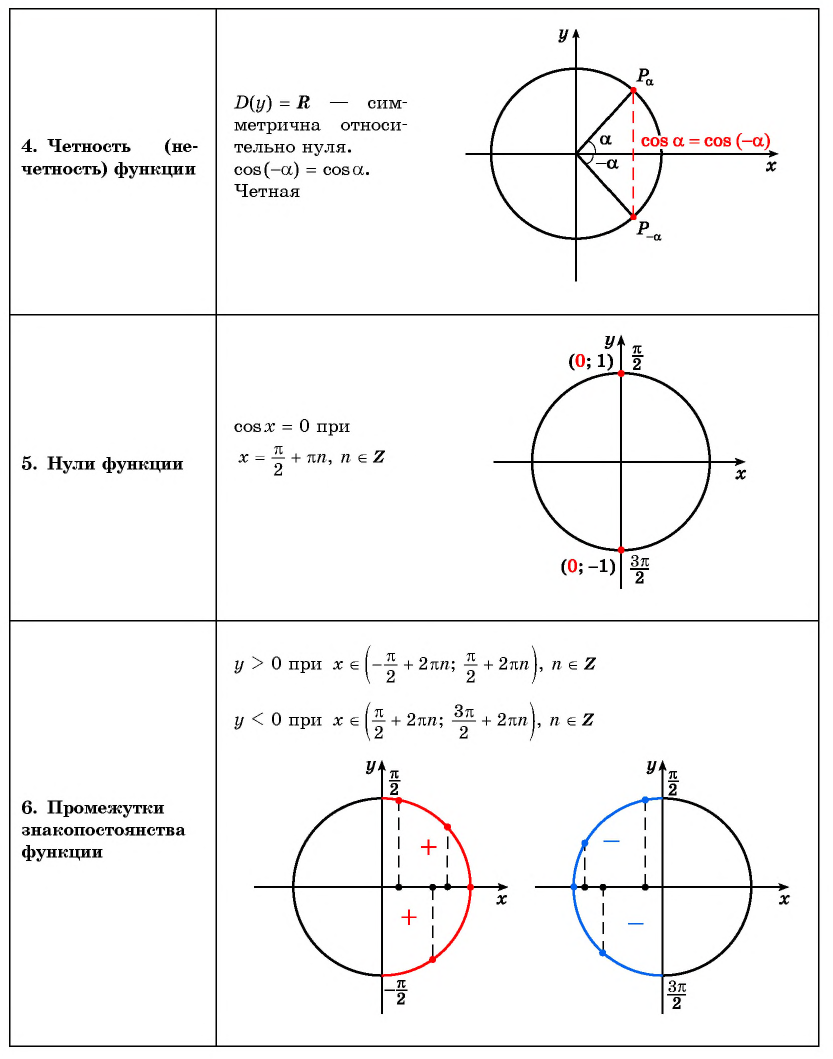
3. Функция чётная $$ cos(-x)=cosx $$
4. Функция периодическая с периодом 2π $$ cos(x+2pi k)=cosx $$
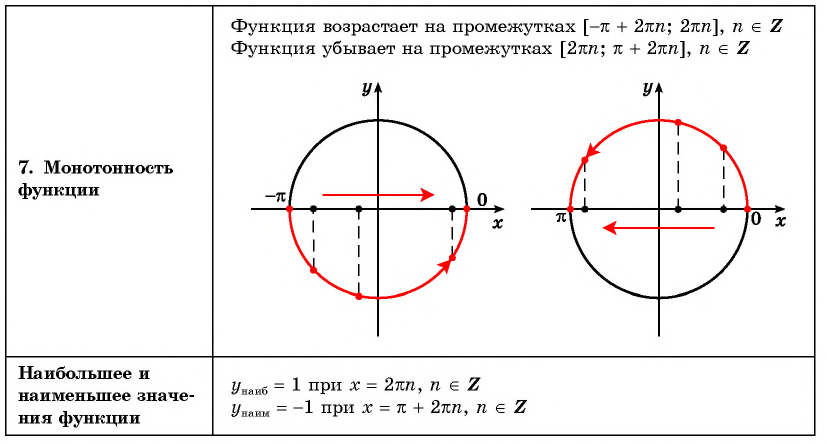
5. Максимальные значения (y_{max}=1) достигаются в точках $$ x=2pi k $$ Минимальные значения (y_{min}=-1) достигаются в точках $$ x=pi+2pi k $$ Нули функции (y_{0}=cosx_0=0) достигаются в точках (x=fracpi2 +pi k)
6. Функция возрастает на отрезках $$ -pi+2pi kleq xleq 2pi k $$ Функция убывает на отрезках $$ 2pi kleq xleqpi+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:
a) (left[fracpi6; frac{3pi}{4}right]) $$ y_{min}=cosleft(frac{3pi}{4}right)=-frac{sqrt{2}}{2}, y_{max}=cosleft(fracpi6right)=frac{sqrt{3}}{2} $$ б) (left[frac{5pi}{6}; frac{5pi}{3}right]) $$ y_{min}=cos(pi)=-1, y_{max}=cosleft(frac{5pi}{3}right)=frac12 $$
Пример 2. Решите уравнение графически:
a) (cosx=fracpi2-x)
Один корень: (x=fracpi2)
б) (cosx-x=1)
(cosx=x+1)
Один корень: x = 0
в) (cosx-x^2=1)
(cosx=x^2+1) 
Один корень: x = 0
г*) (cosx-x^2+frac{pi^2}{4}=0)
(cosx=x^2-frac{pi^2}{4})
(y=x^2-frac{pi^2}{4}) – парабола ветками вверх, с осью симметрии (x_0=0) (ось OY) и вершиной (left(0; -frac{pi^2}{4}right)) (см. §29 справочника для 8 класса)
Два корня: (x_{1,2}=pmfracpi2)
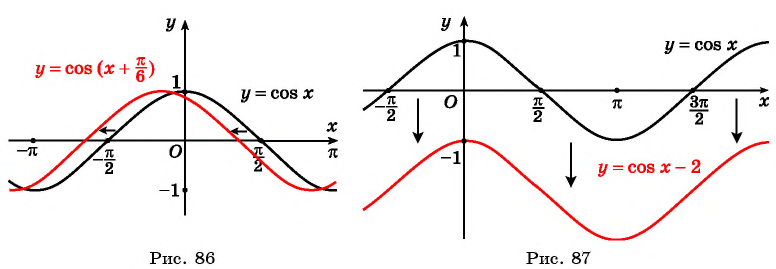
Пример 3. Постройте в одной системе координат графики функций $$ y=cosx, y=-cosx, y=2cosx, y=cosx-2 $$ 
(y=-cosx) – отражение исходной функции (y=cosx) относительно оси OX. Область значений (yin[-1;1]).
(y=2cosx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=cosx-2) – исходная функция опускается вниз на 2. Область значений (yin[-3;-1]).
Пример 4. Постройте в одной системе координат графики функций $$ y=cosx, y=cos2x, y=cosfrac{x}{2} $$ 
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под косинусом изменяет период колебаний.
(y=cosx) – главная арка косинуса соответствует отрезку (-fracpi2leq xleqfracpi2)
(y=cos2x) – период уменьшается в 2 раза, главная арка укладывается в отрезок (-fracpi4leq xleqfracpi4).
(y=cosfrac{x}{2}) – период увеличивается в 2 раза, главная арка растягивается в отрезок (-pi leq xleq pi).
14. Свойства функций синуса, косинуса, тангенса
и котангенса и их графики
14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК
Т а б л и ц а 21
График функции y = sin x (синусоида)
Свойства функции y = sin x
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:
1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями
координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее
З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох
(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордина-
та соответствующей точки единичной окружности
(рис. 79). Поскольку ординату можно найти для
любой точки единичной окружности (в силу того,
что через любую точку окружности всегда можно
провести единственную прямую, перпендикуляр-
ную оси ординат), то область определения функции
y = sin x — все действительные числа. Это можно за-
писать так: D (sin x) = R.
Для точек единичной окружности ординаты нахо-
дятся в промежутке [–1; 1] и принимают все значения
от –1 до 1, поскольку через любую точку отрезка [–1; 1]
оси ординат (который является диаметром единичной
окружности) всегда можно провести прямую, перпендикулярную оси орди-
нат, и получить точку окружности, которая имеет рассматриваемую орди-
нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].
Это можно записать так: E (sin x) = [–1; 1].
Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окружности является точка A, то есть при 
Наименьшее значение функции sin x равно минус единице. Это значение
достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть
при
Как было показано в § 13, синус — нечетная функция: sin(-x)= – sin x,
поэтому ее график симметричен относительно начала координат.
В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом
T = 2π: sin (x + 2π) = sin x , таким образом, через промежутки длиной 2π вид графика функции sin x повторя-
ется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной 2 π , а
потом полученную линию парал лельно перенести вправо и влево вдоль оси Ox на расстояние kT = 2πk , где
k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых sin x, то есть ордината соответствующей точки единичной окруж
ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-
ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).
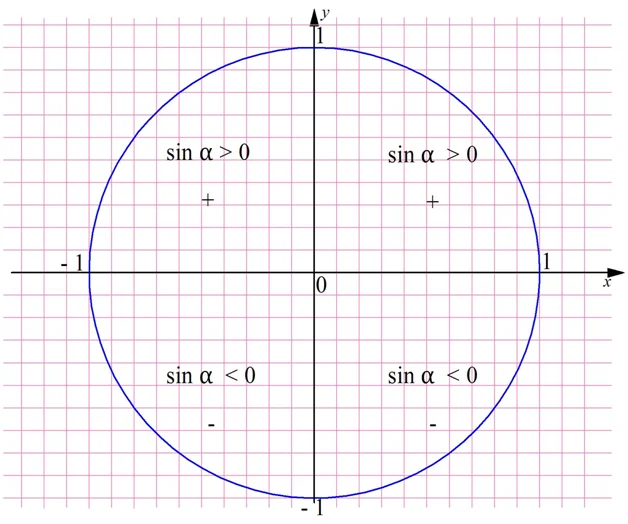
Промежутки знакопостоянства . Как было обосновано в § 13, значения
функции синус положительны (то есть ордината соответствующей точки
единичной окружности положительна) в I и II четвертях (рис. 80). Таким
образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех
x ∈ (2πk; π + 2πk), k ∈ Z.
Значения функции синус отрицательны (то есть ордината соответствую-
щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-
Промежутки возрастания и убывания
Учитывая периодичность функции sin x с периодом T = 2π, достаточно
исследовать ее на возрастание и убывание на любом промежутке длиной
2π, например на промежутке 
то при увеличении аргумента x (x 2 > x 1 ) ордината соответствующей точки единичной окружности увеличивается (то есть
sin x 2 > sin x 1 ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,
делаем вывод, что она такж е возрастает на каждом из промежутков
Если x ∈ 
окружности уменьшается (то есть sin x 2 1 ), таким образом, на этом промежутке функция sin x убывает. Учитывая
периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой
функции (с периодом 2π), д о статочно сначала построить график на любом промежутке длиной 2π, на пример на
промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината
соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на
промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для
построения графика на промежутке [–π; 0] отображаем полученную кривую симметрич но относительно начала координат
Поскольку мы построили график на
промежутке длиной 2π, то, учитывая
периодичность синуса (с периодом 2π),
повторяем вид графика на каждом про-
межутке длиной 2π (то есть переносим па-
раллельно график вдоль оси Ох на 2πk,
где k — целое число).
Получаем график, который называется
З а м е ч а н и е. Тригонометрические функции широко применяются в ма тематике, физике и технике. Например,
множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,
описываются функцией, которая задается формулой y = A sin (ωх + φ). Та кие процессы называют гармоническими
колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль
координатных осей и параллельным пере носом вдоль оси Ох. Чаще всего гармоническое колебание является функцией
времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная
фаза,
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК
Объяснение и обоснование
Напомним, что значение косинуса — это абсцис-
са соответствующей точки единичной окружности
(рис. 85). Поскольку абсциссу можно найти для лю-
бой точки единичной окружности (в силу того, что
через любую точку окружности, всегда можно про-
вести единственную прямую, перпендикулярную оси
абсцисс), то область определения функции y = cos x —
все действительные числа. Это можно записать так:
D (cos x) = R.
Для точек единичной окружности абсциссы нахо-
дятся в промежутке [–1; 1] и принимают все значе-
ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной
всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следователь но, область значений функции y = cos x:
y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это
зна чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окруж ности является точка B, то есть при x = π + 2πk, k ∈ Z.
Как было показано в § 13, косинус — четная функция : cos (–x) = cos x, поэтому ее график симметричен относительно оси
Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом
T = 2π: cos (x + 2π) = cos x. Таким об разом, через промежутки длиной 2π вид графика функции cos x повторяется.
Чтобы найти точки пересечения графика функции с осями координат , напомним, что на оси Oy значение x = 0. Тогда
соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только
тогда, когда на единичной окружности будут выбраны точки C или D, то есть при 
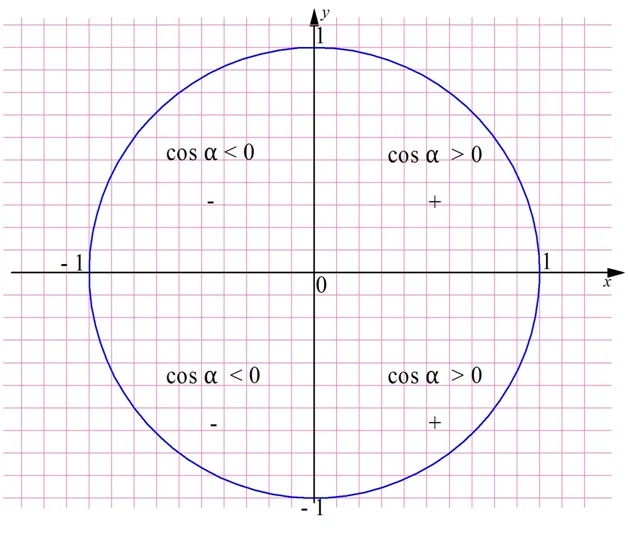
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции косинус положительны (то есть абсцисса соответствующей точки
единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-
тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех 
Значения функции косинус отрицательны (то есть абсцисса соответству-
ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,
поэтому cos x
Промежутки возрастания и убывания
Учитывая периодичность функции cos x (T = 2π), достаточно исследовать
ее на возрастание и убывание на любом промежутке длиной 2π, например
на промежутке [0; 2π].
Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x 2 > x 1 ) абсцисса соответствующей точки единичной
окружности уменьшается (то есть cos x 2 1 ), следовательно, на этом промежутке функция cos x убывает. Учитывая
периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.
Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x 2 > x 1 ) аб-
сцисса соответствующей точки единичной окружности увеличивается (то
есть cos x 2 >cos x 1 ), таким образом, на этом промежутке функция cos x
возрастает. Учитывая периодичность функции cos x, делаем вывод, что
она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.
Проведенное исследование позволяет построить график функции y = cos x
аналогично тому, как был построен график функ-
ции y = sin x. Но график функции у = cos x можно
также получить с помощью геометрических преоб-
разований графика функции у = sin х, используя
Эту формулу можно обосновать, например, так.
Рассмотрим единичную окружность (рис. 88), отметим на ней точки
Функция y = cos x, её свойства и график
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x косинусоидой .
Часть косинусоиды для –π≤x≤π называют волной косинусоиды .
Часть косинусоиды для (-fracpi2leq xleqfracpi2) называют полуволной или аркой косинусоиды .
Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».
п.2. Свойства функции y=cosx
1. Область определения (xinmathbb) – множество действительных чисел.
2. Функция ограничена сверху и снизу $$ -1leq cosxleq 1 $$ Область значений (yin[-1;1])
3. Функция чётная $$ cos(-x)=cosx $$
4. Функция периодическая с периодом 2π $$ cos(x+2pi k)=cosx $$
5. Максимальные значения (y_=1) достигаются в точках $$ x=2pi k $$ Минимальные значения (y_=-1) достигаются в точках $$ x=pi+2pi k $$ Нули функции (y_<0>=cosx_0=0) достигаются в точках (x=fracpi2 +pi k)
6. Функция возрастает на отрезках $$ -pi+2pi kleq xleq 2pi k $$ Функция убывает на отрезках $$ 2pi kleq xleqpi+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1. Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:
a) (left[fracpi6; frac<3pi><4>right]) $$ y_=cosleft(frac<3pi><4>right)=-frac<sqrt<2>><2>, y_=cosleft(fracpi6right)=frac<sqrt<3>> <2>$$ б) (left[frac<5pi><6>; frac<5pi><3>right]) $$ y_=cos(pi)=-1, y_=cosleft(frac<5pi><3>right)=frac12 $$
Пример 2. Решите уравнение графически:
a) (cosx=fracpi2-x)
Один корень: (x=fracpi2)
б) (cosx-x=1)
(cosx=x+1)
Один корень: x = 0
в) (cosx-x^2=1)
(cosx=x^2+1)
Один корень: x = 0
г*) (cosx-x^2+frac<pi^2><4>=0)
(cosx=x^2-frac<pi^2><4>)
(y=x^2-frac<pi^2><4>) – парабола ветками вверх, с осью симметрии (x_0=0) (ось OY) и вершиной (left(0; -frac<pi^2><4>right)) (см. §29 справочника для 8 класса)
Два корня: (x_<1,2>=pmfracpi2)
Пример 3. Постройте в одной системе координат графики функций $$ y=cosx, y=-cosx, y=2cosx, y=cosx-2 $$
(y=-cosx) – отражение исходной функции (y=cosx) относительно оси OX. Область значений (yin[-1;1]).
(y=2cosx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=cosx-2) – исходная функция опускается вниз на 2. Область значений (yin[-3;-1]).
Пример 4. Постройте в одной системе координат графики функций $$ y=cosx, y=cos2x, y=cosfrac <2>$$
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под косинусом изменяет период колебаний.
(y=cosx) – главная арка косинуса соответствует отрезку (-fracpi2leq xleqfracpi2)
(y=cos2x) – период уменьшается в 2 раза, главная арка укладывается в отрезок (-fracpi4leq xleqfracpi4).
(y=cosfrac<2>) – период увеличивается в 2 раза, главная арка растягивается в отрезок (-pi leq xleq pi).
Синус (sin x) и косинус (cos x) – свойства, графики, формулы
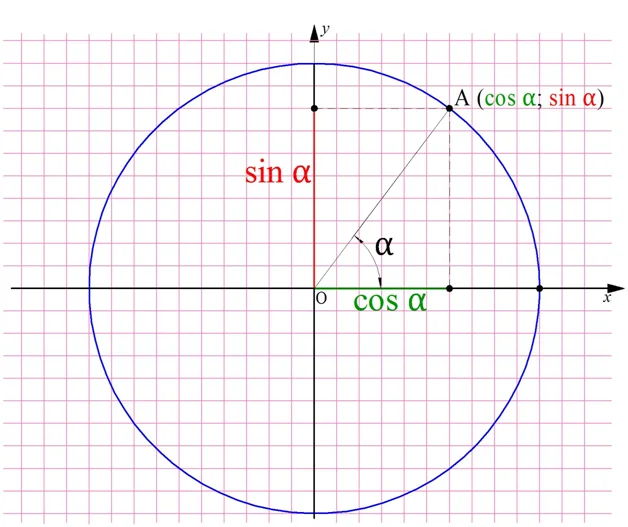
Геометрическое определение синуса и косинуса
α – угол, выраженный в радианах.
Тригонометрическое определение
С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.
На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.
Рис. 2. Тригонометрическое определение синуса и косинуса
Косинус угла – это абсцисса точки. Синус угла – это ордината точки.
На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.
Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол . На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.
Рис. 3. Синус и косинус во II, III и IV четвертях
Табличные значения синуса и косинуса
Абсцисса точки 0 равна 1 , ордината точки 0 равна 0 . Следовательно,
[spoiler title=”источники:”]
http://reshator.com/sprav/algebra/10-11-klass/funkciya-y-cosx-svojstva-i-grafik/
http://calcsbox.com/post/sinus-sin-x-i-kosinus-cos-x-svojstva-grafiki-formuly.html
[/spoiler]
Преподаватель который помогает студентам и школьникам в учёбе.
Содержание:
Некоторые свойства функции
Например, областью определения функции 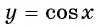
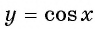
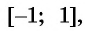
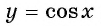
Определение функции y=cos x
Определение:
Зависимость, при которой каждому действительному числу 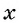
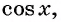
Свойства функции y=cos x
Свойства функции 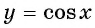
График функции y=cos x
График функции 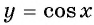
Пример №1
Определите, какие из данных точек принадлежат графику функции
Решение:
а) Подставим в формулу 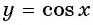
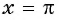
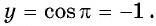
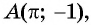
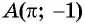
б) При 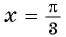
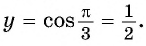
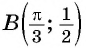
в) При 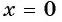
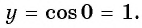
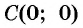
г) При 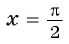
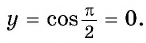
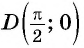
Пример №2
Найдите область определения и множество значений функции
Решение:
Областью определения функции является множество всех действительных чисел, т. е.
Множеством значений функции 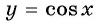
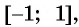
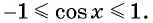
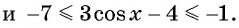
Пример №3
Найдите наименьшее значение функции
Решение:
Так как 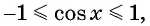
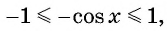
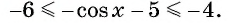
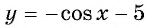
Пример №4
Используя свойство периодичности функции 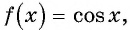
Решение:
Так как число 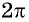
- Заказать решение задач по высшей математике
Пример №5
Используя свойство четности функции 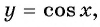
Решение:
Так как функция 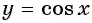
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
а) 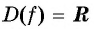
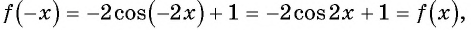
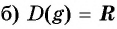
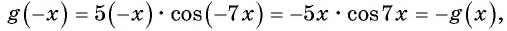
Пример №7
Найдите нули функции:
Решение:
а) Пусть 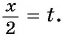
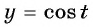
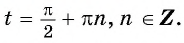
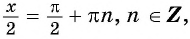
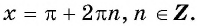
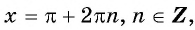
б) Пусть 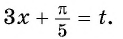
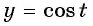
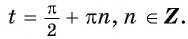
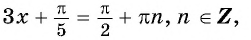
Таким образом, числа 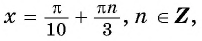
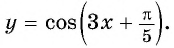
Пример №8
Определите знак произведения
Решение:
Так как 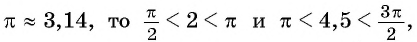
4,5 радиана и 2 радиана принадлежат промежутку 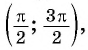
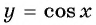
Угол 7 радиан принадлежит промежутку, на котором функция 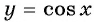
Пример №9
Что больше:
Решение:
Так как функция 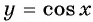
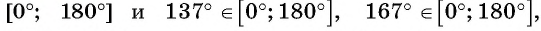
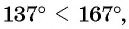
Пример №10
Постройте график функции:
Решение:
а) График функции 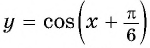
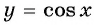
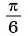
б) График функции 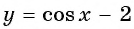
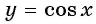
- Функции y=tg x и y=ctg x – их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
Определения
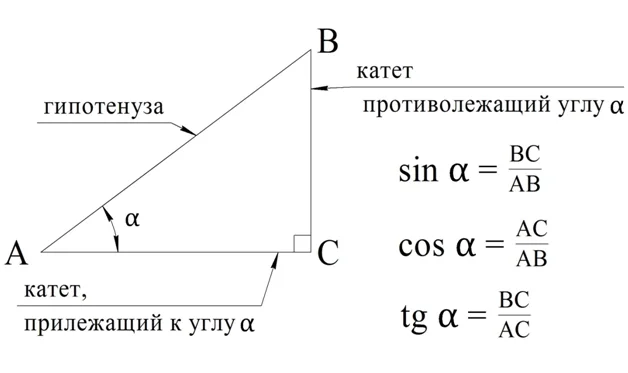
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе.
Синус угла А обозначается sin A.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.
Косинус угла А обозначается cos A.
Наглядно это видно на следующем рисунке:
Функция косинуса: свойства и значения функции косинус
Определение
Функцией косинуса называют элементарную тригонометрическую функцию, выражающую зависимость угла при вершине треугольника от отношения прилежащей его стороны к гипотенузе.
- Основные свойства функции косинус следующие:
- Область определения функции косинуса (значений, которые может принимать аргумент x) – множество всех действительных чисел;
- Значения функции косинус – это (+1) и (-1) и множество действительных чисел между ними.
- Наименьшее значение функции косинус равно 1, а наибольшее – (-1);
- Функция чётная, т. е. cos(-x) = cos(x);
- Функция периодическая. Её период равен 2π;
- Наибольшего своего значения функция косинус x достигает в точках x=2πk;
- Наименьшее значение функции косинус x будет в точках x= π/2+2πk;
- Область возрастания функции cos(x): -π+2πk<=x<=2πk;
- Область убывания функции cos(x): 2πk<= π+2πk;
- Функция не имеет разрывов, т. е. непрерывна.
График функции косинус
Графиком функции является косинусоида. Он получается из графика синуса с помощью параллельного переноса на расстояние [frac{pi}{2}] влево. Он выглядит следующим образом:
Как построить график функции косинус икс
График функции косинуса можно построить следующим образом:
Используем данные единичной окружности, приведённой на рисунке выше.
Из рисунка единичной окружности видно, что в точке ноль ордината функции равна единице. В точке π/2 по оси X значение Y равно 0. В точке π по оси X ордината равна (-1). В точке 3π/2 значение функции снова равно 0, а в точке 2π значение по оси X равно 1. Отметим все названные точки.
Соединим их плавной линией
Т. к. наша функция чётная (свойство №4), её график симметричен оси Y. Зеркально отразим его. Помимо этого нам известно, что период функции равен 2π. Из данного свойства следует неограниченная повторяемость кусочка функции между 0 и 2π в обе стороны вдоль оси X. График функции косинус x построен.
Нет времени решать самому?
Наши эксперты помогут!
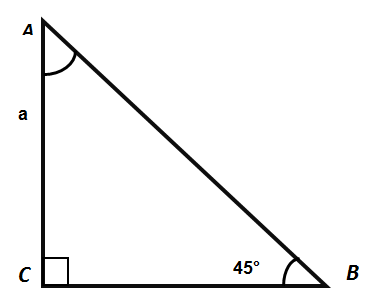
Как найти значение функции косинуса при x равном 45 градусам
Построим прямоугольный треугольник с катетами, равняющимися единице. Сумма углов любого треугольника, как известно, равна 180 градусам. Если вычтем из них прямой угол, получим сумму двух оставшихся углов. Это углы при вершинах A и B. Так как катеты равны, то и выше названные углы равны и каждый из них составляет (180 – 90)/2 = 45 градусов.
По теореме Пифагора гипотенуза его в этом случае будет равна [c=sqrt{a^{2}+a^{2}}=sqrt{1+1}=sqrt{2}]
Из определения косинуса находим [cos (a)=1 / sqrt{2}]
После вычисления и округления числа получим 0,7071. Это и есть косинус 45 градусов.
План урока:
Синус и косинус угла на единичной окружности
График синуса и косинуса
Тангенс угла
График тангенса
Котангенс угла
Синус и косинус угла на единичной окружности
Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:
С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что
ВС = АВ•sinα = 5•0,8 = 4
Если известно, что cosα = 0,6, то мы сможем найти и второй катет:
cosα = АС/АВ
АС = АВ•cosα = 5•0,6 = 3
Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:
tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)
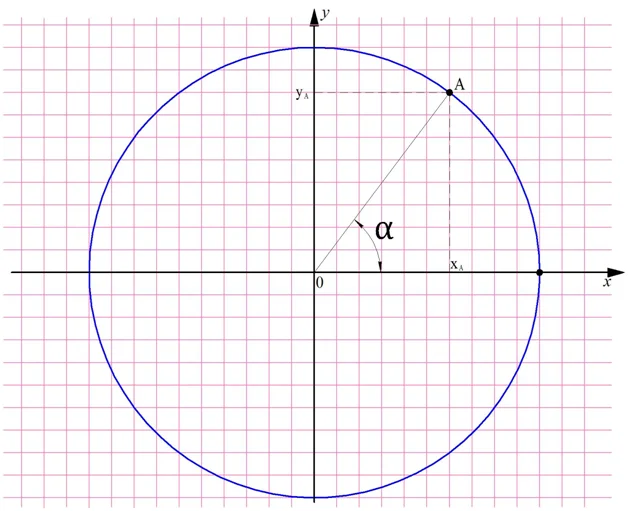
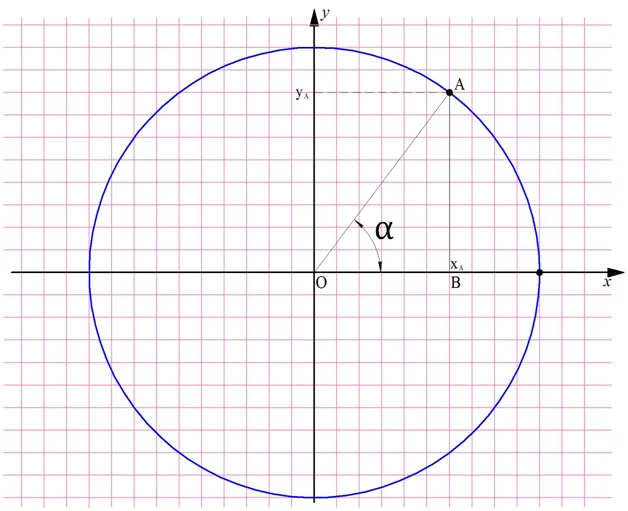
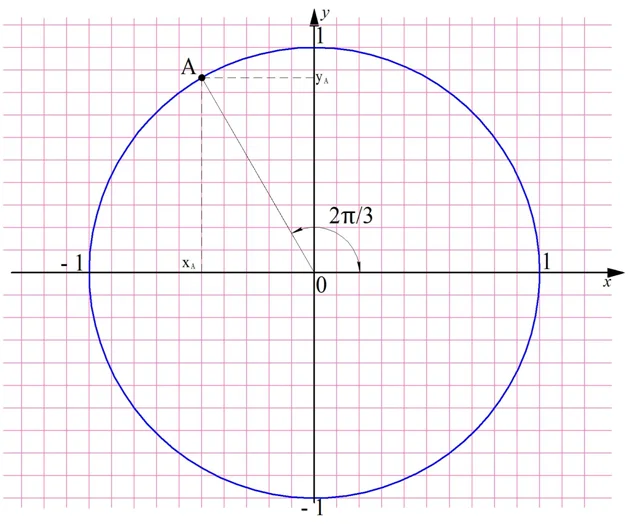
Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты хА и уА:
Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:
Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле
АВ = sinα•ОА
Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда
АВ = sinα•ОА = sinα•1 = sinα
С другой стороны, видно, что величина отрезка АВ равна координате уА. Получается, что уА = АВ = sinα, или
уА = sinα
Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:
ОВ = cosα•ОА
Учитывая, что ОА = 1, а длина ОВ равна координате хА, мы получим следующее:
хА = ОВ = cosα•ОА = cosα•1 = cosα
то есть координата хА равна cos α:
хА = cosα
Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.
Таким образом, нам удалось дать новое определение синусу и косинусу угла:
Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 <α < 90°. На единичной окружности можно отложить любой угол, то есть теперь мы можем вычислять тригонометрические ф-ции для произвольных значений α. При этом синус и косинус могут оказаться отрицательными величинами. Например, для угла α = 2π/3 косинус окажется отрицательным, ведь координата хА соответствующей ему точки окажется левее нуля на горизонтальной оси Ох:
Заметим, что знак синуса и косинуса определяется той четвертью, в которой будет располагаться точка на окружности. Углам в диапазоне 0 <α<π/2 соответствует I четверть, здесь все тригонометрические ф-ции принимают положительные значения. Ко II четверти относятся углы из промежутка π/2 <α<π. Здесь косинус становится меньше нуля, а синус остается положительным. В III четверти будут располагаться точки, соответствующие углам из интервала π <α< 3π/2, у них отрицательны и синус, и косинус. Наконец, к IV четверти относят углы из диапазона 3π/2 <α< 2π. Здесь отрицателен синус, а косинус больше нуля.
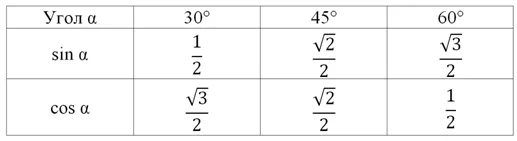
Как же определять значение синуса угла и его косинуса? Из геометрии нам уже известны их значения для трех углов: 30°, 45° и 60°:
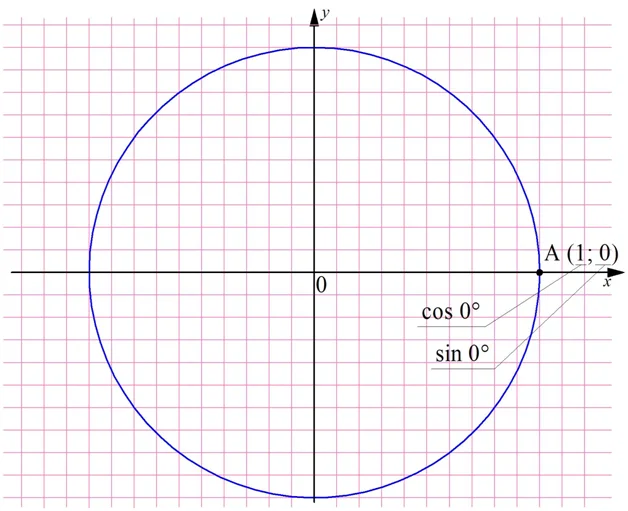
Далее определим тригонометрические ф-ции угла, равного нулю. Если такой угол отложить на единичной окружности, то ему будет соответствовать точка А с координатами (1; 0). Поэтому
sin 0° = уА = 0
cos 0° = xА = 1
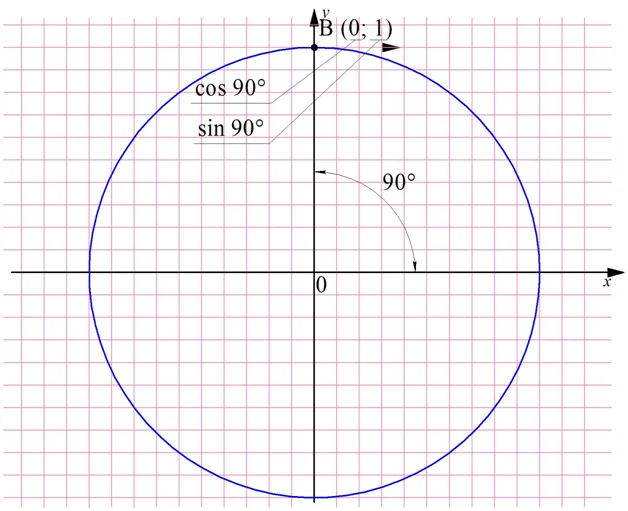
Аналогичным образом можно найти значение этих ф-ций и для угла 90°. Прямому углу на единичной окружности соответствует точка В с координатами (0; 1). Поэтому
sin90° = уВ = 1
cos90° = xВ = 0
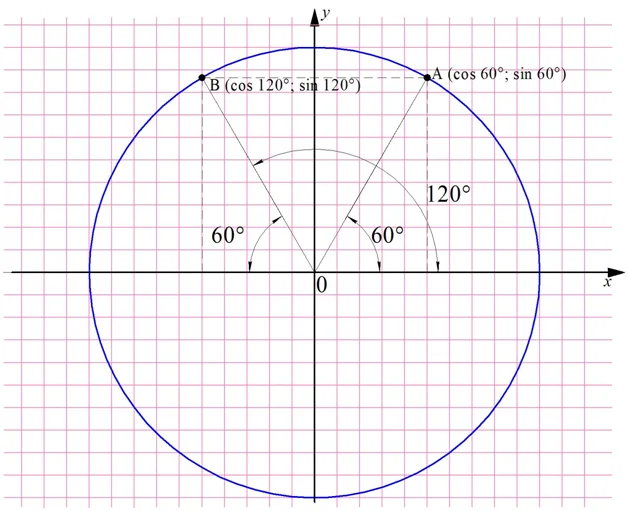
Для определения тригонометрических ф-ций у углов, больших 90°, удобно использовать симметрию. Например, пусть необходимо вычислить синус для угла 120°. Отложим на окружности две точки, В и А. Первая будет соответствовать 120°, а вторая 60°:
Видно, что эти точки находятся на одном горизонтальном уровне, то есть их ординаты (координаты у) одинаковы. При этом абсциссы у них противоположны, ведь точки симметричны относительно оси Оу. Отсюда можно сделать вывод, что
уВ = уА
хВ = – хА
Но координаты А – это синус и косинус 60°, а координаты В являются тригонометрическими ф-циями угла 120°. То есть можно записать
sin 120° = sin 60°
cos 120° = – cos 60°
Так как для угла 60° значения синуса и косинуса нам уже известны, то можно записать:
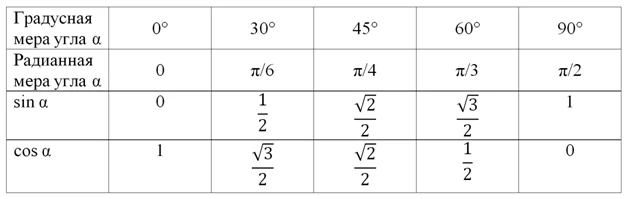
В будущем мы изучим более простые способы вычисления синуса и косинуса углов, больших 90°, когда построения нам уже не потребуются. Однако сразу заметим, что в первую очередь необходимо запомнить значения синуса и косинуса для пяти углов: 0°, 30°, 45°, 60°, 90°. Приведем таблицу значений тригонометрических функций:
Некоторые люди испытывают проблемы с запоминанием этой таблицы. Однако ее можно представить в более простом виде. Заменим числа 0, 1 и 1/2 следующими выражениями с корнями:
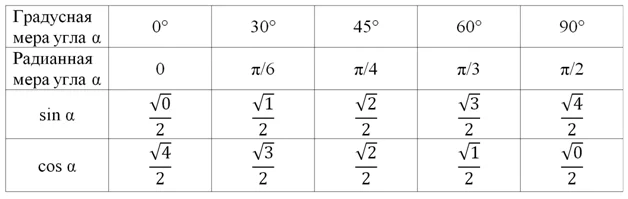
С учетом этого таблицу тригонометрических функций можно переписать так:
Теперь в каждой ячейке стоит дробь, у которой знаменатель равен двум. В числителе же стоит корень. Обратите внимание, что у синуса под корнем последовательно стоят числа 0, 1, 2, 3, и 4. У косинуса эти же числа идут в обратном порядке – от четверки до нуля. В таком виде таблицу запомнить проще.
Для вычисления тригонометрических ф-ций углов, не попадающих в диапазон 0 ⩽ α < 2π их надо привести к этому самому диапазону. Напомним, что для этого можно просто добавить к углу несколько полных оборотов, или отнять их.
Задание. Вычислите cos 7π/3.
Решение. Угол 7π/3 равен углу π/3:
7π/3 = 6π/3 + π/3 = 2π + π/3 = π/3
Значит, и косинус у угла 7π/3 будет равен косинусу угла π/3:
cos 7π/3 = cosπ/3 = 1/2
Ответ: 1/2.
График синуса и косинуса
Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток [– 1; 1].
Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).
Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.
Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.
Мы знаем, что
sin 0 = 0
sin π/6 = 1/2
sin π/2 = 1
Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:
С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:
Теперь соединим их плавной кривой:
Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:
Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:
Получили ещё два участка графика, на промежутках [– 2π; 0] и [2π; 4π]. Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:
В результате мы получили кривую, которую называют синусоидой.
Теперь построим график косинуса. Мы знаем что
cos 0 = 1
cos π/3 = 1/2
cos π/2 = 1
Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:
Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:
Соединяем эти точки плавной линией:
Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:
Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток [– 1; 1]:
Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.
В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:
sin (x+ 2π) = sinx
cos (x+ 2π) = sinx
В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является нечетной функцией, а косинус – четной функцией. Напомним, что ф-ция f(x) является нечетной, если справедливо условие
f(x) = – f(– x)
Если f(x) – четная ф-ция, то должно выполняться условие:
f(x) = f(– x)
Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:
Поэтому верны формулы:
sin (– α) = – sinα
cos (– α) = cosα
Тангенс угла
Синус и косинус являются основными, или, как говорят математики, прямыми тригонометрическими ф-циями. Однако есть ещё две производных тригонометрических ф-ций – тангенс и котангенс. Напомним, что тангенс угла в прямоугольном треугол-ке – это отношение противолежащего катета к прилежащему. Однако в тригонометрии куда удобнее пользоваться другим его определением. Тангенс – это отношение синуса угла к его косинусу:
Для получения тангенса на единичной окружности необходимо продолжить прямую, образующую угол α, до её пересечения с прямой х = 1. Точка их пересечения будет иметь координаты (1; tgα):
Заметим, что если α относится ко второй четверти, то тангенс получится отрицательным. Действительно, с одной стороны, соответствующая прямая пересечет линию х = 1 в точке, лежащей ниже оси Ох:
С другой стороны, мы знаем, что во второй четверти синус положителен, а косинус – отрицателен. Тогда их отношение, то есть тангенс, должно быть отрицательным:
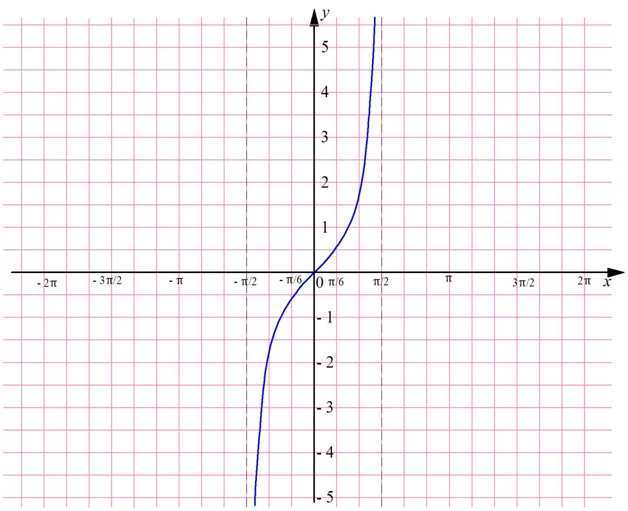
Очевидно, что тангенс должен быть периодической ф-цией. Однако его период вдвое меньше 2π и составляет π. Действительно, углы, отличающиеся на π, будут иметь одинаковое значение тангенса, что видно из построения:
Это значит, что справедлива формула:
tg(α + π) = tg α
С другой стороны, это означает, что тангенсы углов из III четверти положительны, ведь они равны тангенсам углов из I четверти. Аналогично можно утверждать, что тангенсы углов из IV четверти отрицательны:
Также тангенс является нечетной ф-цией. Чтобы убедиться в этом, найдем с помощью единичной окружности tgα и tg (– α):
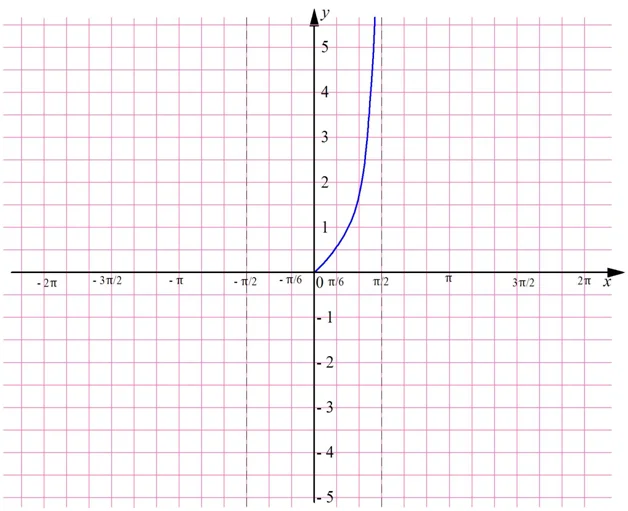
Из построения видно, что tg (– α) = tgα, поэтому тангенс попадает под определение нечетной ф-ции.
Доказать этот факт можно и иначе. Вспомним, что синус – это нечетная ф-ция, а косинус – четная. Тогда, используя определение тангенса, можно записать:
Для вычисления тангенса проще всего использовать его определение. Мы знаем синусы и косинусы стандартных углов, а потому, деля их друг на друга, сможем найти и тангенсы стандартных углов:
Ещё раз отметим, что важнее всего запомнить значения синусов и косинусов стандартных углов. Зная их, школьник всегда сможет самостоятельно вычислить тангенс.
Можно ли вычислить тангенс для угла π/2, то есть для 90°? Сделать это не получится, ведь cosπ/2 равен нулю. Если подставить cosπ/2 в формулу для вычисления тангенса, то получится деление на ноль! Так как тангенс – периодическая ф-ция, то его нельзя вычислить и в тех точках, которые отличаются от π/2 на целое число π.
В частности, тангенс не определен при х = – π/2.
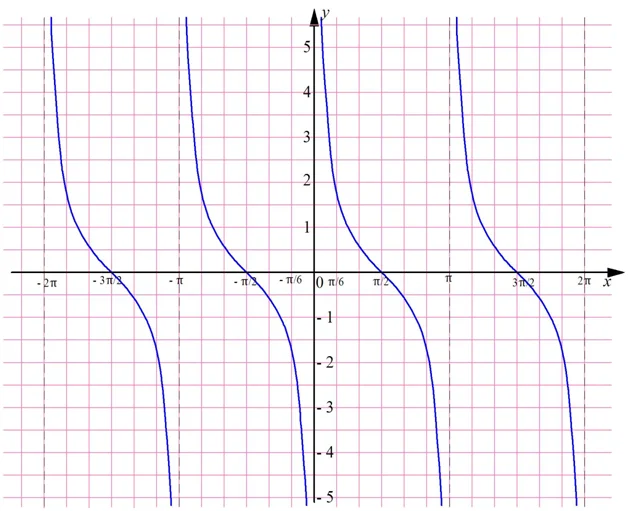
График тангенса
Так как тангенс обладает периодом, равным π, достаточно построить его график на каком-нибудь промежутке длиной π. Далее его можно будет просто перенести на π единиц влево и вправо. Удобно выбрать промежуток от – π/2 до π/2. Дело в том, что на нем она определена во всех точках, кроме его концов.
Через точки х = – π/2 и х = π/2 проведем штриховые линии – они означают, что график НЕ должен пересекать их. Ясно, что график проходит через точку (0; 0), ведь tg 0 = 0. Тангенс представляет собой дробь sinx/cosx. При увеличении х от 0 до π/2 знаменатель возрастает, а числитель убывает, стремясь к нулю. Поэтому вся дробь неограниченно растет, и график тангенса возрастает до бесконечности:
Так как мы строим график нечетной ф-ции, то мы можем полученную ветвь отобразить симметрично относительно начала координат:
Полученный график называют тангенсоидой. Осталось воспользоваться тем, что мы рассматриваем периодическую ф-цию с периодом π, и перенести тангенсоиду влево и вправо:
Котангенс угла
Помимо тангенса в тригонометрии выделяют ещё одну производную ф-цию – котангенс. Он представляет отношение косинуса к синусу:
Видно, что определение котангенса очень похоже определение тангенса. В принципе, удобней использовать несколько другую формулу:
Почти во всех задачах с помощью формулы
можно избавиться от котангенса, заменив его дробью 1/tgα. Поэтому мы вкратце расскажем об основных особенностях котангенса, ведь он очень редко используется на практике.
Значения этой ф-ции рассчитываются так:
При х = 0 значение котангенса не определено, так как в этой точке косинус становится равным нулю, а деление на ноль невозможно.
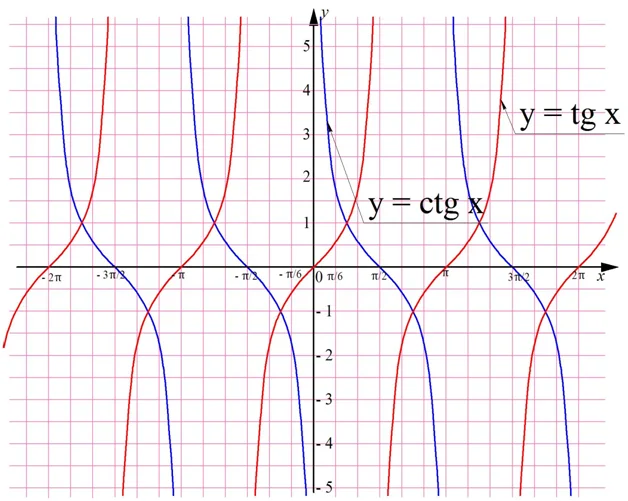
График котангенса – это тангенсоида, которая отображена симметрично относительно оси Ох и смещена на π/2:
Можно заметить, что вертикальные штриховые линии (асимптоты) графика проходят через точки, кратные π: –2π, – π, 0, π, 2π… Они разбивают координатную прямую на интервалы (– 2π; – π), (– π; 0), (0; π), (π; 2π), на каждом из которых ф-ция у = ctgx убывает. Видно, что котангенс – это периодическая ф-ция с периодом π.
Для сравнения покажем на одной плоскости графики тангенса и котангенса:
Котангенс, как и тангенс – нечетная ф-ция, то есть
ctg (– x) = – ctgx
Теперь у нас есть представление об основных тригонометрических ф-циях. Важнейшими из них являются синус и косинус. Тангенс является производной ф-цией от них и рассчитывается как отношение синуса к косинусу. Редко используемый котангенс, наоборот, представляет собой отношение косинуса к синусу.
Впервые элементы тригонометрии стали использовать ещё древние греки, которые производили с их помощью астрономические расчеты. В XVIII веке Эйлер сформулировал определения тригонометрических функций с помощью единичной окружности, благодаря которым стало возможным вычислять их значение для любых углов. Изначально тригонометрия использовалась для географических расчетов и навигации, однако со временем область ее применения расширилась. Оказалось, что без неё не обойтись в анализе финансовых рынков и биологических процессов, архитектуре, акустике и оптике, теории вероятностей.