Как найти косинус картинки - Сайт, где вы сможете решить свои вопросы

Чтобы найти косинус угла по клеточкам, следует вспомнить, что это собственно за величина – косинус.

По определению, косинус – это отношение прилежащего катета к гипотенузе.

Зная это определение мы очень легко можем найти косинус любого прямоугольного треугольника, нарисованного на клеточках. То есть если задан просто угол, мы достраиваем его до прямоугольного треугольника:

Разберем несколько случаев.

Катеты расположены вертикально и горизонтально. Тогда их длину определяем по клеточкам, а длину гипотенузы по теореме Пифагора.

Катеты расположены произвольно. Заключаем треугольник в прямоугольник и находим катеты и гипотенузу по теореме Пифагора для всех трех сторон. Дальше находим косинус как отношение по определению.

Например здесь катет АО находится как корень из 20 (16+4). Гипотенуза ОВ находится как корень из 37 (36+1). Их отношение – косинус угла АОВ.

Если треугольник АОВ не получается прямоугольным, то имеет смысл использовать теорему косинусов:

Источник

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол A обозначается соответствующей греческой буквой alpha .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла alpha , называется противолежащим (по отношению к углу alpha ). Другой катет , который лежит на одной из сторон угла alpha , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle c}.$

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A $=genfrac{}{}{}{0}{displaystyle b}{displaystyle c}.$

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle b}.$

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A $=genfrac{}{}{}{0}{displaystyle sin A}{displaystyle cos A}.$

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A $=genfrac{}{}{}{0}{displaystyle cos A}{displaystyle sin A}.$

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin $displaystyle alpha = frac{a}{c}$	sin ${}^2 alpha +$ cos $displaystyle {}^2 alpha =1$	$alpha + beta = 90 ^{circ}$
cos $displaystyle alpha = frac{b}{c}$	1+tg $displaystyle {}^2 alpha =frac{1}{cos ^2 alpha}$	cos = sin
tg $displaystyle alpha = frac{a}{b}$	1+ctg $displaystyle {}^2 alpha =frac{1}{sin ^2 alpha}$	sin = cos
ctg $displaystyle alpha = frac{b}{a}$		tg = ctg

Давайте докажем некоторые из них.

Сумма углов любого треугольника равна $180^{circ}$ . Значит, сумма двух острых углов прямоугольного треугольника равнa $90^{circ}$ .
С одной стороны, $sin A =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ как отношение противолежащего катета к гипотенузе. С другой стороны, $cos B =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, $cos left( 90^{circ}-A right) = sin A$ .
Возьмем теорему Пифагора: . Поделим обе части на получаем $displaystyle left ( frac{a}{c} right )^2+left ( frac{b}{c} right )^2=left ( frac{c}{c} right )^2 ,$ то есть
Мы получили основное тригонометрическое тождество.
Поделив обе части основного тригонометрического тождества на , получим: $1+tg ^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos ^2 A }.$ Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично, $1+ctg ^2 A =genfrac{}{}{}{0}{1}{sin ^2 A }.$

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна $180^{circ}$ .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от $0^{circ}$ до $90^{circ}$ .

	0	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 6}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 4}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 3}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 2}$
sin	0	$displaystyle frac{1}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{sqrt{3}}{2}$
cos		$displaystyle frac{sqrt{3}}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{1}{2}$	0
tg	0	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$			−
ctg	−			$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$	0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и C_1 и равными острыми углами А и A_1.

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому $displaystyle frac{AB}{A_1 B_1}=frac{BC}{B_1 C_1}=frac{AC}{A_1 C_1 } .$

Из этих равенств следует, что $displaystyle frac{BC}{AB}=frac{B_1 C_1}{A_1 B_1} ,$ т. е. sin А = sin A_1.

Аналогично, $displaystyle frac{AC}{AB}=frac{A_1C_1}{A_1 B_1},$ т. е. cos А = cos A_1, и $displaystyle frac{BC}{AC}=frac{B_1C_1}{A_1 C_1},$ т. е. tg A = tg A_1.

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен $90^{circ}$ , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку $A+B = 90^{circ}$ , sin A = cos B = 0,1.

Задача 2. В треугольнике ABC угол равен $90^{circ}$ , AB=5 , $sin A = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}$ .

Найдите .

Решение:

$sin A = genfrac{}{}{}{0}{displaystyle a}{displaystyle c} = genfrac{}{}{}{0}{displaystyle BC}{displaystyle AB} = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.$

Отсюда

$BC= genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25} cdot AB = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 5}.$

Найдем AC по теореме Пифагора.

$AC=sqrt{AB^2-BC^2} = genfrac{}{}{}{0}{displaystyle 24}{displaystyle 5} = 4,8.$

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против Значит, sin A $displaystyle = frac{BC}{AB}= frac{5}{13}.$

Катет, прилежащий к angle A – это катет АС, следовательно, cos⁡ А $displaystyle = frac{AC}{AB}=frac{AC}{13}.$

Длину катета АС найдем по теореме Пифагора:

Тогда $AC = sqrt{AB^2-BC^2}=sqrt{(13)^2-5^2}=sqrt{144}=12.$

cos⁡ А $displaystyle = frac{12}{13}=0,923 ... approx 0,92 ;$

tg A $displaystyle = frac{BC}{AC} = frac{5}{12}=0,416...approx 0,42.$

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен AC = 2, sin A= $displaystyle frac{sqrt{17}}{17} .$

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A $displaystyle = frac{a}{c} = frac{BC}{AB} = frac{sqrt{17}}{17},$ $displaystyle frac{a}{c} = frac{sqrt{17}}{17} ,$ $displaystyle c = frac{17a}{sqrt{17}}=sqrt{17}a.$

По теореме Пифагора получим

$a^2+2^2=(sqrt{17} a)^2;$

$displaystyle a= frac{1}{2}=0,5;$

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен AC = 4, tg A = $displaystyle frac{33}{4sqrt{33}} .$ Найдите AB.

Решение:

AC = b = 4, tg A $displaystyle = frac{a}{b}=frac{33}{4sqrt{33}},$

$displaystyle frac{a}{4}=frac{33}{4sqrt{33}},$ $displaystyle a=frac{4 cdot 33}{4 cdot sqrt{33}}=sqrt{33},$

$AB = c = sqrt{a^2+b^2}=sqrt{(sqrt{33})^2+4^2}=sqrt{33+16} =7.$

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = $displaystyle frac{1}{5} .$ Найдите AH.

Решение:

AВ = с = 13, tg A = $displaystyle frac{a}{b}=frac{1}{5} ,$ тогда b = 5a.

По теореме Пифагора ABC:

$displaystyle a=sqrt{frac{169}{26}}=frac{13}{sqrt{26}},$ тогда $displaystyle b = 5a=5cdot frac{13}{sqrt{26}}=frac{65}{sqrt{26}}.$

(по двум углам), следовательно $displaystyle frac{AH}{AC}=frac{AC}{AB} ,$ откуда

$displaystyle AH = frac{AC^2}{AB}=frac{b^2}{c}=left ( frac{65}{sqrt{26}}right )^2:13=12,5.$

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен

CH – высота, BC = 3, sin A = $displaystyle frac{1}{6} .$

Найдите AH.

Решение:

Так как sin A = $displaystyle frac{a}{c} = frac{BC}{AB} = frac{1}{6},$ тогда $displaystyle frac{3}{c} = frac{1}{6} ,$ c = АВ = 18.

sin A = $displaystyle frac{a}{c}$ = cos⁡ B = $displaystyle frac{1}{6} .$

Рассмотрим BHC:

${cos B= }displaystyle frac{BH}{BC}$ = $displaystyle frac{1}{6} ,$ получим $displaystyle frac{BH}{3}=displaystyle frac{1}{6},$

тогда BH = $displaystyle frac{3}{6}=displaystyle frac{1}{2}$ = 0,5,

AH = AB – BH = 18 – 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BC = 3, cos A = $displaystyle frac{sqrt{35}}{6}.$

Найдите АH.

Решение:

Так как для АВС: cos A = $displaystyle frac{AC}{AB}=$ sin В = $displaystyle frac{sqrt{35}}{6},$

а для ВНС: sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{sqrt{35}}{6}$ , откуда СН = $displaystyle frac{BC cdot sqrt{35}}{6}=displaystyle frac{3 cdot sqrt{35}}{6}=displaystyle frac{sqrt{35}}{2},$

По теореме Пифагора найдем ВН:

$BH = sqrt{{BC}^2-{CH}^2}=sqrt{3^2-{left(displaystyle frac{sqrt{35}}{2}right)}^2}=$

$=sqrt{9-displaystyle frac{35}{4}}=sqrt{displaystyle frac{1}{4}}=displaystyle frac{1}{2}=0,5.$

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:

${CH}^2=AH cdot BH,$ тогда $AH= displaystyle frac{ {CH}^2}{BH}, ; AH= displaystyle frac{ {left(displaystyle frac{sqrt{35}}{2}right)}^2}{0,5}=displaystyle frac{35 cdot 2}{4}=17,5.$

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ =

Рассмотрим BHC : ${cos B= }displaystyle frac{BH}{BC}.$

ВС найдем по теореме Пифагора:

ВС= $sqrt{{BH}^2+{CH}^2}=sqrt{7^2+{24}^2}=sqrt{49+576}=sqrt{625}=25,$

тогда ${cos B= }displaystyle frac{BH}{BC}=displaystyle frac{7}{25}=0,28,$ а значит и sin A = = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ = cos A = $displaystyle frac{b}{c}$ = $displaystyle frac{AC}{AB}$ =

тогда tg A = $displaystyle frac{sin A}{{cos A }}=displaystyle frac{cosB}{sinB}=ctgB,$ который найдем из BHC:

$ctgB=displaystyle frac{BH}{CH}=displaystyle frac{4}{8}=0,5.$

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, tg A = $displaystyle frac{2}{3}.$ Найдите АН.

Решение:

По определению tg A= $displaystyle frac{BC}{AC}=ctgB=displaystyle frac{2}{3}.$

Для BHC: $ctgB=displaystyle frac{BH}{CH}=displaystyle frac{2}{3}$ , значит $displaystyle frac{12}{CH}=displaystyle frac{2}{3},$ СН = $displaystyle frac{12 cdot 3}{2}=18.$

Для АHC: tg A= $displaystyle frac{CH}{AH}=displaystyle frac{2}{3},$ то $displaystyle frac{18}{AH}=displaystyle frac{2}{3},$ AH = $displaystyle frac{18 cdot 3}{2}=27.$

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, sin A = $displaystyle frac{2}{3}.$ Найдите АВ.

Решение:

Так как cos В = $displaystyle frac{BC}{AB}$ = sin A = $displaystyle frac{2}{3}.$

Из СВН имеем cos В = $displaystyle frac{HB}{BC}$ = $displaystyle frac{2}{3},$ тогда ВС = $displaystyle frac{3 cdot HB}{2}=displaystyle frac{3 cdot 12}{2}=18.$

В АВС имеем sinA = $displaystyle frac{BC}{AB}$ = $displaystyle frac{2}{3},$ тогда AВ = $displaystyle frac{3 cdot BC}{2}=displaystyle frac{3 cdot 18}{2}=27.$

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 ${}^circ,$ из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из ВСН:

$HB = sqrt{BC^2-BH^2}=sqrt{20^2-12^2}=sqrt{(20-12)(20+12)}=$

sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{12}{20}=displaystyle frac{3}{5}.$

Для АВС: cos A = $displaystyle frac{AC}{AB}=sin B=displaystyle frac{3}{5},$ получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = $displaystyle frac{AC}{AB}=displaystyle frac{3}{5},$ то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора ${AC}^2+{BC}^2= {AB}^2,$ получим ${(3x)}^2+{(20)}^2= {(5x)}^2$
${25x}^2-{9x}^2= {20}^2 ,$

${16x}^2= {20}^2,$

$x^2= {left(displaystyle frac{20}{4}right)}^2,$
х = 5 ( так как х0). Значит,

2-й способ.

(по двум углам), значит $displaystyle frac{HB}{CB}=frac{HC}{AC}=frac{BC}{AB}$ или $displaystyle frac{16}{20}={12}{AC}={20}{AB} = k,$

k = $displaystyle frac{16}{20}=displaystyle frac{4}{5} ,$ тогда $displaystyle frac{12}{AC}=displaystyle frac{4}{5},$ АС = $displaystyle frac{12 cdot 5}{4}=15$ ; $displaystyle frac{20}{AB}=displaystyle frac{4}{5},$ АВ = $displaystyle frac{20 cdot 5}{4}=25.$

3-й способ.

${CH}^2=AH cdot HB$ (высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда ${12}^2=AH cdot 16,$ АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{25}^2-{20}^2}=sqrt{(25-20)(25+20)}$ =

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = $sqrt{{HC}^2+{BH}^2}=sqrt{{18}^2+{24}^2}=sqrt{324+576}$ =

cos C = $displaystyle frac{HC}{BC}=displaystyle frac{18}{30}=displaystyle frac{3}{5}.$

Для АВС: sin А = $displaystyle frac{BC}{AC}$ = cos C = $displaystyle frac{3}{5}.$

Для АНВ: sin А = $displaystyle frac{BH}{AB}$ = $displaystyle frac{3}{5},$ то $displaystyle frac{24}{AB}$ = $displaystyle frac{3}{5},$ АВ = $displaystyle frac{24 cdot 5}{3}=40.$

Из основного тригонометрического тождества найдем

cos A = $sqrt{1-{sin}^2A}=sqrt{1-0,36}=sqrt{0,64}=0,8.$

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А = $displaystyle frac{7}{25}.$

Найдите площадь треугольника.

Решение:

В прямоугольном АСЕ sin А = $displaystyle frac{CE}{AC},$

значит $displaystyle frac{7}{25}$ = 14.

Второй катет найдем, используя теорему Пифагора: $AE= sqrt{{AC}^2-{CE}^2};$

$AE = sqrt{{50}^2-{14}^2}=sqrt{(50-14)(50+14)} =sqrt{36cdot 64}=6cdot8=48.$

Площадь прямоугольного треугольника равна S = $displaystyle frac{1}{2}ab,$

поэтому $S_{ACE}= displaystyle frac{1}{2} AEcdot CE=displaystyle frac{48cdot 14}{2}=336.$

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin Результат округлите до сотых.

Решение:

A-общий, $angle AKC=angle ACB=90{}^circ$ ),

значит sin $angle ACK=displaystyle frac{AK}{AC}=displaystyle frac{AC}{AB}.$

Найдем АС по теореме Пифагора из САВ:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{13}^2-{12}^2}=$

Тогда sin $angle ACK=displaystyle frac{5}{13}=0,384..approx 0,38.$

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = $displaystyle frac{12}{13}.$ Найдите высоту СН.

Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ = $displaystyle frac{1}{2}AB=36.$

Поскольку АСН — прямоугольный,

cos A = $displaystyle frac{AH}{AC}=$ $displaystyle frac{12}{13},$ то есть $displaystyle frac{36}{AC}=$ $displaystyle frac{12}{13}$ АС = $displaystyle frac{36 cdot 13}{12}=39.$

По теореме Пифагора ${AH}^2+{CH}^2={AC}^2,$ тогда

$CH = sqrt{{AC}^2-{AH}^2} = sqrt{{39}^2-{36}^2}=$

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 ${}^circ,$ sin A = $displaystyle frac{11}{14},$ AC = 10 Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = $displaystyle frac{BC}{AB}=$ $displaystyle frac{11}{14},$ то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора $AC^2+{BC}^2={AB}^2;$

${(10sqrt{3})}^2+{(11x)}^2={(14x)}^2;$

${(14x)}^2-{(11x)}^2 = 3 cdot 100;$

(14х- 11х)(14х + 11х) = 3 cdot 100;

x^2=4, учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 cdot 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством ${sin}^2A+{cos}^2A=1;$

cos A = $sqrt{1-{sin}^2A}=sqrt{1-{left(displaystyle frac{11}{14}right)}^2}=sqrt{displaystyle frac{196-121}{196}}=sqrt{displaystyle frac{75}{196}}=displaystyle frac{5sqrt{3}}{14}.$

По определению cos A = $displaystyle frac{AC}{AB},$ значит $displaystyle frac{AC}{AB}= displaystyle frac{5sqrt{3}}{14}.$

Так как АС=10 то $displaystyle frac{10sqrt{3}}{AB}= displaystyle frac{5sqrt{3}}{14},$ откуда АВ = $displaystyle frac{10sqrt{3} cdot 14}{5sqrt{3}}$ = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 sqrt{3} и 4.

Решение:

Пусть angle ВАО = alpha .

Диагонали ромба делят его углы пополам, значит, = alpha .

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = $displaystyle frac{1}{2} AC=2sqrt{3},$ а катет ВО = $displaystyle frac{1}{2}BD =2.$

Поэтому tg $alpha =displaystyle frac{BO}{AO}=displaystyle frac{2}{2sqrt{3}}=displaystyle frac{1}{sqrt{3}},$ откуда $alpha =30{}^circ .$

$angle BAD=2alpha =60{}^circ , ; angle ADC=angle ABC=180{}^circ -60{}^circ =120{}^circ .$

Ответ: ${60}^circ,$ ${120}^circ,$ ${60}^circ,$ ${120}^circ .$

Часто в задачах встречаются треугольники с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ или с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ катет, лежащий напротив угла в $30^{circ}$ , равен половине гипотенузы.

Треугольник с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ — равнобедренный. В нем гипотенуза в sqrt{2} раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 ${}^circ,$ угол А равен 30 ${}^circ,$ АВ = 2

Найдите высоту CH.

Решение:

Рассмотрим АВС:

По свойству катета, лежащего против угла ${30}^circ,$ имеем ВС = $displaystyle frac{1}{2}$ АВ =

В BHC: $angle BHC=90{}^circ ,; angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно, ВН = $displaystyle frac{1}{2}$ BC = $displaystyle frac{sqrt{3}}{2}.$

По теореме Пифагора найдем НС:

$HC = sqrt{{BC}^2-{BH}^2}=sqrt{{left(sqrt{3}right)}^2-{left(displaystyle frac{sqrt{3}}{2}right)}^2}=sqrt{3-displaystyle frac{3}{4}}=$

$=sqrt{2displaystyle frac{1}{4}}=sqrt{displaystyle frac{9}{4}}=displaystyle frac{3}{2}=1,5.$

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, АВ = 2, $angle A=30{}^circ .$ Найдите АH.

Решение:

Из АВС найдем ВС = $displaystyle frac{1}{2}$ АВ = 1 (по свойству катета, лежащего против угла 30 ${}^circ$ ),

$angle A=30{}^circ ,$ то $angle B=60{}^circ .$

Из ВСН: $angle BHC=90{}^circ , angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно,

ВН = $displaystyle frac{1}{2}$ ВС = $displaystyle frac{1}{2}.$

АН = АВ — НВ = 2 – $displaystyle frac{1}{2}$ = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.

Синус, косинус, тангенс и котангенс. Определения

Зачем разделять понятия синуса, косинуса, тангенса и котангенса?

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Что такое синус?

Синус угла (sin α) – это отношение противолежащего этому углу катета к гипотенузе.

Что такое косинус?

Косинус угла (cosα) – это отношение прилежащего катета к гипотенузе.

Что такое тангенс?

Тангенс угла (tg α) – это отношение противолежащего катета к прилежащему.

Котангенс угла (ctg α) – отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

Синус и косинус можно представить через экспоненту (экспоненциальная функция).

Приведем иллюстрацию.

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.

Что и почему важно и принято помнить в ходе такого нахождения?

Важно помнить!

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг – вся числовая прямая, то есть эти функции могут принимать любые значения.

Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором – теорему косинусов.

Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы.

Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).

Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.

Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).

Синус (sin или син) угла поворота

Синус угла поворота α – это ордината точки A1(x , y). sin α=y

Косинус (cos) угла поворота

Косинус угла поворота α – это абсцисса точки A1(x , y). cos α=икс

Тангенс (tg) угла поворота

Тангенс угла поворота α – это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx

Котангенс (ctg) угла поворота

Котанг угла поворота α – это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Важно помнить!

Простое правило: синус и косинус определены для любых углов α.

Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)

Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)

При решении практических примеров не говорят “синус угла поворота α”. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10π равен синусу угла поворота величиной 10π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности – точка A c координатами (1, 0).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t=y

Косинус (cos) числа t

Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t=x

Тангенс (tg) числа t

Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α, cos α, tg α, ctg α – это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс – основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α=A1HOA1=y1=y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Синус, косинус, тангенс и котангенс: основные формулы

Источник

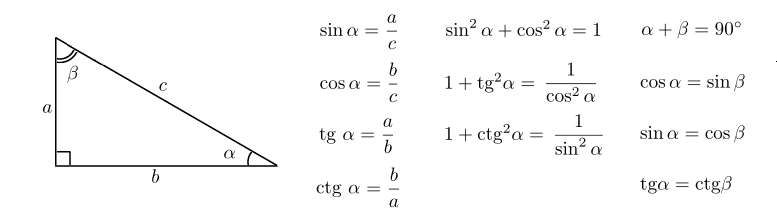
В статье про прямоугольный треугольник посмотрели задачи связанные с синусами и косинусами из 1 части ОГЭ. Так что обязательно заглядывай.

Получается, что решить прямоугольный треугольник (найти все стороны и острые углы) можно довольно просто, зная всего лишь два элемента прямоугольного треугольника :две стороны (по теореме Пифагора) или сторону и острый угол (из определений синуса, косинуса, тангенса).

Но решить треугольник (найти все стороны и углы ) можно и произвольный, зная три элемента: три стороны, две стороны и угол, или два угла и сторону.

Для первых двух случаев в решении пользуются теоремой косинусов (вполне возможно эта тема вас поджидает уже на следующей неделе в школе, а может уже и была):

в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.

Если известны три стороны треугольника можно найти косинусы всех углов
Если известны две стороны и угол между ними треугольника, то можно найти третью сторону.

В этом случае полезно пользоваться таблицей значений косинусов некоторых углов :

Рассмотрим решение задачи №16 из сборника Ященко (36 вариантов) на теорему косинусов :

Изобразим треугольник АВС и найдем в нем противолежащую сторону для угла АВС.

Из рисунка видно, что противолежащая сторона – это сторона АС.

Для стороны АС записываем теорему косинусов:

Подставим значения всех сторон:

Переносим все “свободные” числа (меняя знак) в левую часть равенства и считаем:

Находим косинус угла АВС, как неизвестный множитель:

Записываем ответ:

Если вы знаете того, кто готовится к ОГЭ, не забудьте поделиться с ним этой информацией. Всегда пригодится.

Продолжение следует…

Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

(✿◠‿◠)

Источник

В статье мы расскажем, как находить значения:

(cos300^°), (sin⁡(-540^°)), (cos 510^°), (sin⁡(-135^°))

и других тригонометрических выражений без тригонометрической таблицы.

Как вычисляются синусы и косинусы углов?

Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен – абсциссе, а синус угла – ординате.

Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.

Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Получается, (cos 30^° = frac{sqrt{3}}{2}), а (sin⁡30^° =frac{1}{2}).

Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:

В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».

Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac{1}{2}=±0,5); (±frac{sqrt{2}}{2} ≈±0,707); (±frac{sqrt{3}}{2} ≈±0,866).

Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.

Как отметить любой угол на тригонометрическом круге?

Для этого нужно знать несколько фактов:

Начало отсчета находится в крайней правой точке окружности;
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:

Одна точка может соответствовать разным углам;

Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.

Пример. Отметьте угол в (90^° ) и (-90^°).
Решение:

Пример. Отметьте угол в (225^° ) и (-135^°).
Решение: (225^°=180^°+45^°)
(-135^°=-90^°-45^°)

Пример. Отметьте угол в (420^° ) и (-390^°).
Решение: (420^°=360^°+60^°)
(-390^°=-360^°-30^°)

Задание 1. Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).

Как находить синус и косинус любого угла?

Простой алгоритм:

Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
Найдите координаты точки, используя картинку ниже.

Пример. Вычислите (sin⁡300^°) и (cos⁡300^°) .
Решение: (⁡300^°=360^°-60^°)

(cos⁡ 300^°=frac{1}{2}), (sin⁡{300^°}=-frac{sqrt{3}}{2}).

Пример . Вычислите (sin⁡(-540^°)) и (cos(-540^°)) .
Решение. (-540^°=-360^°-180^°).

(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos⁡(-540^°)=-1), а (sin⁡(-540^° )=0).

Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье.

Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).

Примеры вычисления синуса и косинуса из ЕГЭ

В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.

Пример . Найдите значение выражения (-18sqrt{2}sin⁡(-135^°)).
Решение. (-135^°=-90^°-45^°)

Получается (-18sqrt{2} sin⁡(-135^° )=-18sqrt{2}cdot-frac{sqrt{2}}{2}=frac{18cdotsqrt{2}cdotsqrt{2}}{2}=9cdot 2=18.)
Ответ: (18).

Пример . Найдите значение выражения (54sqrt{3}cos⁡(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)

(54sqrt{3}cos⁡(510^°)=54sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{54cdot sqrt{3}cdot sqrt{3}}{2}=-27cdot 3=-81.)
Ответ: (-81).

Смотрите также:
Как найти тангенс и котангенс без тригонометрической таблицы? Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?

Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов

Источник

Синус, косинус и тангенс острого угла прямоугольного треугольника

Синус, косинус, тангенс и котангенс. Определения

Угол поворота

Числа

Тригонометрические функции углового и числового аргумента

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Синус, косинус, тангенс и котангенс: основные формулы

Продолжение следует…

Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

(✿◠‿◠)

Как вычисляются синусы и косинусы углов?

В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».

Как отметить любой угол на тригонометрическом круге?

Как находить синус и косинус любого угла?

Примеры вычисления синуса и косинуса из ЕГЭ

Вам также может понравиться

Как составить письмо если ты должен

Жесткий диск грузится на 100 процентов windows 10 как исправить

Ошибка director player error как исправить

Добавить комментарий Отменить ответ