Как найти косинус не табличного угла - Сайт, где вы сможете решить свои вопросы

В статье мы расскажем, как находить значения:

(cos300^°), (sin⁡(-540^°)), (cos 510^°), (sin⁡(-135^°))

и других тригонометрических выражений без тригонометрической таблицы.

Как вычисляются синусы и косинусы углов?

Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен – абсциссе, а синус угла – ординате.

Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.

Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Получается, (cos 30^° = frac{sqrt{3}}{2}), а (sin⁡30^° =frac{1}{2}).

Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:

В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».

Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac{1}{2}=±0,5); (±frac{sqrt{2}}{2} ≈±0,707); (±frac{sqrt{3}}{2} ≈±0,866).

Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.

Как отметить любой угол на тригонометрическом круге?

Для этого нужно знать несколько фактов:

Начало отсчета находится в крайней правой точке окружности;
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:

Одна точка может соответствовать разным углам;

Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.

Пример. Отметьте угол в (90^° ) и (-90^°).
Решение:

Пример. Отметьте угол в (225^° ) и (-135^°).
Решение: (225^°=180^°+45^°)
(-135^°=-90^°-45^°)

Пример. Отметьте угол в (420^° ) и (-390^°).
Решение: (420^°=360^°+60^°)
(-390^°=-360^°-30^°)

Задание 1. Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).

Как находить синус и косинус любого угла?

Простой алгоритм:

Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
Найдите координаты точки, используя картинку ниже.

Пример. Вычислите (sin⁡300^°) и (cos⁡300^°) .
Решение: (⁡300^°=360^°-60^°)

(cos⁡ 300^°=frac{1}{2}), (sin⁡{300^°}=-frac{sqrt{3}}{2}).

Пример . Вычислите (sin⁡(-540^°)) и (cos(-540^°)) .
Решение. (-540^°=-360^°-180^°).

(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos⁡(-540^°)=-1), а (sin⁡(-540^° )=0).

Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье.

Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).

Примеры вычисления синуса и косинуса из ЕГЭ

В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.

Пример . Найдите значение выражения (-18sqrt{2}sin⁡(-135^°)).
Решение. (-135^°=-90^°-45^°)

Получается (-18sqrt{2} sin⁡(-135^° )=-18sqrt{2}cdot-frac{sqrt{2}}{2}=frac{18cdotsqrt{2}cdotsqrt{2}}{2}=9cdot 2=18.)
Ответ: (18).

Пример . Найдите значение выражения (54sqrt{3}cos⁡(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)

(54sqrt{3}cos⁡(510^°)=54sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{54cdot sqrt{3}cdot sqrt{3}}{2}=-27cdot 3=-81.)
Ответ: (-81).

Смотрите также:
Как найти тангенс и котангенс без тригонометрической таблицы? Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?

Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов

Источник

Все категории

Фотография и видеосъемка
Знания
Другое
Гороскопы, магия, гадания
Общество и политика
Образование
Путешествия и туризм
Искусство и культура
Города и страны
Строительство и ремонт
Работа и карьера
Спорт
Стиль и красота
Юридическая консультация
Компьютеры и интернет
Товары и услуги
Темы для взрослых
Семья и дом
Животные и растения
Еда и кулинария
Здоровье и медицина
Авто и мото
Бизнес и финансы
Философия, непознанное
Досуг и развлечения
Знакомства, любовь, отношения
Наука и техника

Как посчитать не табличное значение синуса или косинуса???По какой формуле, каким вообще местом??Распишите пожалуйста. Для приме

Как посчитать не табличное значение синуса или косинуса???
По какой формуле, каким вообще местом??
Распишите пожалуйста. Для примера: синус и косинус 75 градусов

1 ответ:

0

0

Для вычисления синуса или косинуса пользуются формулами синус (косинус) суммы или разности “табличных” углов

cos(α+β)=cosα*cosβ-sinα*sinβ

cos(α-β)=cosα*cosβ+sinα*sinβ

sin(α+β)=sinα*cosβ+cosα*sinβ

sin(α-β)=sinα*cosβ-cosα*sinβ

Например 75°=45°+30°

sin75=sin(45+30)=sin45*cos30+cos45*sin30=

$frac{sqrt{2}}{2}*frac{sqrt{3} }{2} +frac{sqrt{2} }{2} *frac{1}{2}=frac{sqrt{6}+sqrt{2} }{4}$

cos75=cos(45+30)=cos45*cos30-sin45*sin30= $frac{sqrt{2}}{2}*frac{sqrt{3} }{2} -frac{sqrt{2} }{2} *frac{1}{2}=frac{sqrt{6}-sqrt{2} }{4}$

Как найти косинус

Косинус является одной из основных тригонометрических функций. Согласно определения данная величина представляет численное выражение отношения прилежащего катета (в прямоугольном треугольнике) к гипотенузе. Для нахождения величины cos угла можно воспользоваться данными о сторонах треугольника, формулами приведения или же тригонометрическими тождествами. С каждым из способов более подробно познакомимся далее.

1

Нахождение величины косинуса по определению

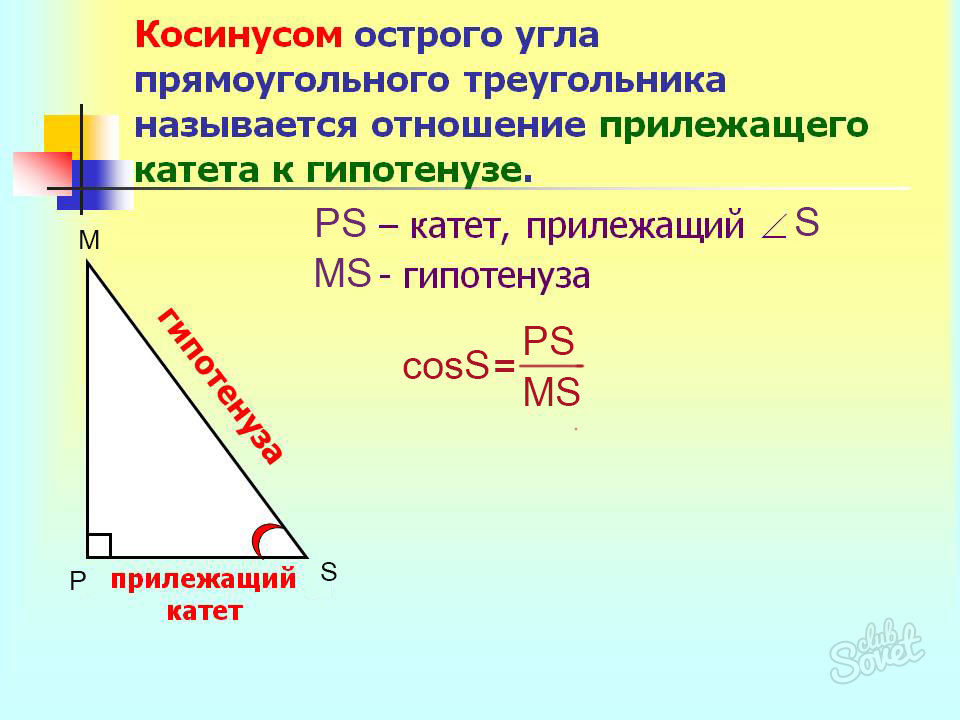
Определение косинуса “привязывает” данную тригонометрическую функцию с прямоугольному треугольнику. Итак, перед вами указанная фигура – треугольник MSP, ∠P = 90°. Тогда:

cosM = MP/MS,
cosS = PS/MS, где
MP и PS – прилежащие (для каждого конкретного угла) катеты,
MS – гипотенуза заданного треугольника.

2

Нахождение величины косинуса угла между векторами

Пересечение направленных отрезков прямой – векторов – ведет к образованию углов. Найти их косинус (а, значит, в последствии и градусную меру) позволяет определение скалярного произведения векторов. Данная формулировка предполагает перемножение длин векторов на косинус угла, образованного в результате их пересечения. Т.о., если у вас есть 2 направленных отрезка ū и ō, то

ūō = ū *ō = (ū, ō) = lūl * lōl * cos (ū,ˆ ō), ⇒
cos (ū,ˆ ō) = (ū, ō) / lūl * lōl.
В проекции на координаты декартовой системы направленные отрезки имеют параметры ū (x,y) = (u(x) ,u(y)) и ō (x,y) = (o(x), o(y)). Значит соотношение приобретает следующий вид:
cos (ū,ˆ ō) = (u(x)*o(x) + u(y)*o(y)) / lūl * lōl = (u(x)*o(x) + u(y)*o(y)) / (√(u(x)²+ u(y)²) * √o(x)² + o(y)²).

Если направленные отрезки заданы не на плоскости, а в пространстве, добавляется третья координата – z. Выражение нахождения косинуса преобразуется и будет иметь следующий вид:

cos (ū,ˆ ō) = (u(x)*o(x) + u(y)*o(y) + u(z)*o(z)) / lūl * lōl = (u(x)*o(x) + u(y)*o(y) + u(z)*o(z)) / (√(u(x)²+ u(y)² + u(z)²) * √o(x)² + o(y)² + o(z)².

3

Нахождение величины косинуса с помощью формул приведения

Работая с формулами приведения для косинуса, необходимо понимать и помнить важное правило – переход от функции к кофункции (в данном случае переход от cos к sin) происходит при 90° и 270°. При 180° и 360° такой трансформации не будет. Исходя из этого, справедливыми будут следующие соотношения:

cos(π/2 – μ) = sinμ,
cos(π/2 + μ) = -sinμ,
cos(π – μ) = cos(π + μ) = -cosμ,
cos(3π/2 – μ) = -sinμ,
cos(3π/2 + μ) = sinμ,
cos(2π – μ) = cos(2π + μ) = cosμ, где
μ – угол поворота.

Т.к. косинус является периодической функцией с периодом 2πk, где k – произвольное целое значение, в общем случае выражения приведения приобретут следующий вид:

cos(μ + 2πk) = cos(-μ + 2πk) = cosμ,
cos(π/2 – μ + 2πk) = sinμ,
cos(π/2 + μ + 2πk) = -sinμ,
cos(π – μ + 2πk) = cos(π + μ + 2πk) = -cosμ,
cos(3π/2 – μ + 2πk) = -sinμ,
cos(3π/2 + μ + 2πk) = sinμ,
cos(2π – μ + 2πk) = cos(2π + μ + 2πk) = cosμ.

4

Нахождение величины косинуса через тригонометрические тождества

Данные тождества представляют собой выражения (равенства), справедливые для угла любой градусной меры.

cos²μ + sin²μ = 1 ⇒ cos²μ = 1 – sin²μ ⇒ cosμ = ±√ 1 – sin²μ
tgμ = sinμ / cosμ ⇒ cosμ = sinμ / tgμ
ctgμ = cosμ / sinμ ⇒ cosμ = ctgμ * sinμ
1/cos²μ = tg²μ + 1 ⇒ cos²μ = 1 / (tg²μ + 1) ⇒ cosμ = ± 1 / √tg²μ + 1

5

Нахождение косинуса угла – табличные величины

Для каждого угла, градусная мера которого находится в промежутке от 0° до 360°, можно определить соответствующее значение косинуса, воспользовавшись одноименной таблицей. Наиболее распространенными и часто используемыми являются следующие константы:

cos0° = 1, cos90° = 0,
cos30° = √3/2, cos180° = -1,
cos60° = 1/2, cos360° = 1.
cos45° = √2/2,

Источник

Как вычисляются синусы и косинусы углов?

В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».

Как отметить любой угол на тригонометрическом круге?

Как находить синус и косинус любого угла?

Примеры вычисления синуса и косинуса из ЕГЭ

Как посчитать не табличное значение синуса или косинуса???По какой формуле, каким вообще местом??Распишите пожалуйста. Для приме

Как найти косинус

1 Нахождение величины косинуса по определению

2 Нахождение величины косинуса угла между векторами

3 Нахождение величины косинуса с помощью формул приведения

4 Нахождение величины косинуса через тригонометрические тождества

5 Нахождение косинуса угла – табличные величины

Вам также может понравиться

Как найти другие острова в эндер мире

Как найти платежи по фамилии

Домашнее вино скисло как исправить

Добавить комментарий Отменить ответ

1

Нахождение величины косинуса по определению

2

Нахождение величины косинуса угла между векторами

3

Нахождение величины косинуса с помощью формул приведения

4

Нахождение величины косинуса через тригонометрические тождества

5

Нахождение косинуса угла – табличные величины