Как найти косинус не табличного значения

В статье мы рассмотрим, как найти значения:

(cosfrac{π}{6}),       (sin⁡(-frac{7π}{3})),     (cosfrac{3π}{4}),     (sin⁡(-frac{27π}{2}))

и других тригонометрических выражений без тригонометрической таблицы.

Для начала внимательно прочтите статью о числовой окружности. Вы должны научиться находить точки на окружности в числах с Пи.

Уже умеете? Тогда два ключевых утверждения:

Например, пусть нам нужно найти синус и косинус числа (frac{π}{6}). Обозначим на числовой окружности точку со значением (frac{π}{6}).

Если построить все точно и крупно, то можно убедиться, что абсцисса этой точки будет равна (0,866…) , что соответствует числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Значит, что (cos⁡(frac{π}{6}) = frac{sqrt{3}}{2}), а (sin(frac{π}{6}) ⁡=frac{1}{2}).

Аналогично и для любой другой точки: значение абсциссы совпадает со значением косинуса, а ординаты – синуса. Поэтому:

И обычно на них не наносят значения в десятичных ((0,1); (0,2); (0,3) и т.д.), а сразу отмечают стандартные значения для синуса и косинуса: (frac{1}{2} =0,5); (frac{sqrt{2}}{2} ≈0,707); (frac{sqrt{3}}{2}≈0,866), причем, как со знаком плюс, так и минус. Почему стандартные значения синуса и косинуса именно (frac{1}{2}),(frac{sqrt{2}}{2}) и (frac{sqrt{3}}{2}) вы можете узнать из этого видео.

Как находить значения синуса и косинуса без таблицы, а только с помощью круга?

Алгоритм прост:

1. Начертите круг и оси косинусов и синусов.
2. Отметьте на круге число, синус и косинус которого надо найти. Если с этим возникают проблемы, прочитайте здесь о том, как расставлять числа на числовой окружности. 
3. Найдите координаты точки, используя картинку ниже.

Пример. Найдите синус и косинус для числа (-frac{7π}{6}).
Решение:(-frac{7π}{6}=-frac{6π}{6}-frac{π}{6}=-π-frac{π}{6}) , то есть, чтобы отметить на окружности точку (-frac{7π}{6}) сначала находим число (-π) и от него в отрицательную сторону откладываем дугу длиной (frac{π}{6}).

Отмечаем число, синус и косинус которого надо найти:

Получается, что (sin⁡(-frac{7π}{6})=frac{1}{2}), (cos⁡(-frac{7π}{6})=-frac{sqrt{3}}{2}).

Пример. Вычислите (sinfrac{5π}{2}) и (cosfrac{5π}{2}).
Решение:  (frac{5π}{2}=frac{4π+π}{2}=frac{4π}{2}+frac{π}{2}=2π+frac{π}{2}).

Точка (frac{5π}{2}) совпадает с (1) на оси синусов, значит (sin⁡frac{5π}{2}=1). А если провести перпендикуляр из точки (frac{5π}{2}) до оси косинусов, то можно убедиться, что он попадет в (0). Поэтому (cosfrac{5π}{2}=0).

И тут некоторые из вас подумали: «с кругом, на котором подписаны числа, каждый дурак сможет посчитать, а что делать, когда его под рукой нет? Что делать на ЕГЭ?» Ответ прост – нарисуйте круг сами! Для этого вам будет нужно понять логику расположения чисел на осях (подробнее об этом читайте в статье «Как запомнить тригонометрический круг»).

Пример. Найдите а) (sin⁡frac{3π}{2}), б) (cos⁡frac{3π}{4}), в) (sin⁡(-frac{π}{3})) .
Решение: а) Чертим круг, оси и отмечаем число (frac{3π}{2}). Обращаем внимание на ось синусов и понимаем, что точка совпала с (-1), получается (sin⁡frac{3π}{2}=-1).
б) (frac{3π}{4}=frac{4π}{4}-frac{π}{4}=π-frac{π}{4}) – отмечаем число на круге. Проводим перпендикуляр до оси косинусов и вспоминаем, что точки со знаменателем (4) находятся посередине. Мы еще попали и в отрицательную часть оси косинусов, получается (cos⁡frac{3π}{4}=-frac{sqrt{2}}{2}).
в) (-frac{π}{3}) – отмечаем число на круге. Видим, что перпендикуляр к оси синусов попал в точку близкую к (-1), значит (sin⁡(-frac{π}{3})=-frac{sqrt{3}}{2}).

Как видите не обязательно рисовать, очень красивую или очень большую окружность – вы можете определить нужное вам значение, быстро набросав круг. И ничего не надо учить!

Если вы хотите еще примеров с вычислением синусов и косинусов без тригонометрической таблицы, то прочтите эту статью.

Пример (ЕГЭ). Найдите значение выражения (frac{8}{sin⁡(-frac{27π}{4}) cos⁡(frac{31π}{4})}) .
Решение.    (-frac{27π}{4}=-frac{28π}{4}+frac{π}{4}=-7π+frac{π}{4}).
(frac{31π}{4}=frac{32π}{4}-frac{π}{4}=8π-frac{π}{4}).

(sin⁡(-frac{27π}{4})=-frac{sqrt{2}}{2}),      (cos⁡(frac{31π}{4})=frac{sqrt{2}}{2}).

(frac{8}{sin⁡(-frac{27π}{4}) cos⁡(frac{31π}{4})})(=) (frac{ 8}{-frac{sqrt{2}}{2}cdotfrac{sqrt{2}}{2}})(=-8:frac{2}{4}=-8cdotfrac{2}{1}=-16).

Ответ: (-16).

Смотрите также:
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?

Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов

Михаил Григорьев

Мыслитель

(5304)


3 года назад

Как найти синус и косинус без тригонометрической таблицы?

В статье мы рассмотрим, как найти значения:

и других тригонометрических выражений без тригонометрической таблицы .

Для начала внимательно прочтите статью о числовой окружности . Вы должны научиться находить точки на окружности в числах с Пи .

Уже умеете? Тогда два ключевых утверждения:

– косинус числа равен абсциссе точки на числовой окружности
– синус числа равен ординате точки на числовой окружности

Например, пусть нам нужно найти синус и косинус числа (frac<π><6>). Обозначим на числовой окружности точку со значением (frac<π><6>).

Если построить все точно и крупно, то можно убедиться, что абсцисса этой точки будет равна (0,866…) , что соответствует числу (frac<sqrt<3>><2>) , а ордината равна (0,5), то есть (frac<1><2>).

Аналогично и для любой другой точки: значение абсциссы совпадает со значением косинуса, а ординаты – синуса. Поэтому:

В тригонометрии ось абсцисс часто называют «ось косинусов», а ординат – «ось синусов».

И обычно на них не наносят значения в десятичных ((0,1); (0,2); (0,3) и т.д.), а сразу отмечают стандартные значения для синуса и косинуса: (frac<1> <2>=0,5); (frac<sqrt<2>> <2>≈0,707); (frac<sqrt<3>><2>≈0,866), причем, как со знаком плюс, так и минус. Почему стандартные значения синуса и косинуса именно (frac<1><2>),(frac<sqrt<2>><2>) и (frac<sqrt<3>><2>) вы можете узнать из этого видео .

Как находить значения синуса и косинуса без таблицы, а только с помощью круга?

1. Начертите круг и оси косинусов и синусов.
2. Отметьте на круге число, синус и косинус которого надо найти. Если с этим возникают проблемы, прочитайте здесь о том, как расставлять числа на числовой окружности.
3. Найдите координаты точки, используя картинку ниже.

Пример. Найдите синус и косинус для числа (-frac<7π><6>).
Решение:(-frac<7π><6>=-frac<6π><6>-frac<π><6>=-π-frac<π><6>) , то есть, чтобы отметить на окружности точку (-frac<7π><6>) сначала находим число (-π) и от него в отрицательную сторону откладываем дугу длиной (frac<π><6>).

Отмечаем число, синус и косинус которого надо найти:

Точка (frac<5π><2>) совпадает с (1) на оси синусов, значит (sin⁡frac<5π><2>=1). А если провести перпендикуляр из точки (frac<5π><2>) до оси косинусов, то можно убедиться, что он попадет в (0). Поэтому (cosfrac<5π><2>=0).

И тут некоторые из вас подумали: «с кругом, на котором подписаны числа, каждый дурак сможет посчитать, а что делать, когда его под рукой нет? Что делать на ЕГЭ?» Ответ прост – нарисуйте круг сами! Для этого вам будет нужно понять логику расположения чисел на осях (подробнее об этом читайте в статье « Как запомнить тригонометрический кру г »).

Пример. Найдите а) (sin⁡frac<3π><2>), б) (cos⁡frac<3π><4>), в) (sin⁡(-frac<π><3>)) .
Решение: а) Чертим круг, оси и отмечаем число (frac<3π><2>). Обращаем внимание на ось синусов и понимаем, что точка совпала с (-1), получается (sin⁡frac<3π><2>=-1).
б) (frac<3π><4>=frac<4π><4>-frac<π><4>=π-frac<π><4>) – отмечаем число на круге. Проводим перпендикуляр до оси косинусов и вспоминаем, что точки со знаменателем (4) находятся посередине. Мы еще попали и в отрицательную часть оси косинусов, получается (cos⁡frac<3π><4>=-frac<sqrt<2>><2>).
в) (-frac<π><3>) – отмечаем число на круге. Видим, что перпендикуляр к оси синусов попал в точку близкую к (-1), значит (sin⁡(-frac<π><3>)=-frac<sqrt<3>><2>).

Как видите не обязательно рисовать, очень красивую или очень большую окружность – вы можете определить нужное вам значение, быстро набросав круг. И ничего не надо учить!

Если вы хотите еще примеров с вычислением синусов и косинусов без тригонометрической таблицы, то прочтите эту статью.

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Тригонометрия: Таблица значений тригонометрических функций

0 °
30 °
45 °
60 °
90 °

sin α
0
1 2
2 2
3 2
1

cos α
1
3 2
2 2
1 2
0

tg α
0
3 3
1
3
нет

ctg α
нет
3
1
3 3
0

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

Нахождение значений синуса, косинуса, тангенса и котангенса

Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.

В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.

Рассмотрим подробно каждый случай.

Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.

Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.

Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.

В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.

Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.

Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .

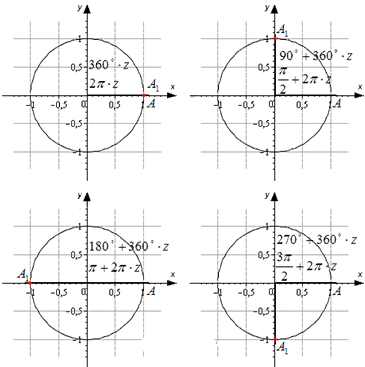
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z – любое целое число.

Изобразим данные формулы на рисунке:

Для каждой группы соответствуют свои значения.

При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .

Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.

Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .

Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.

Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.

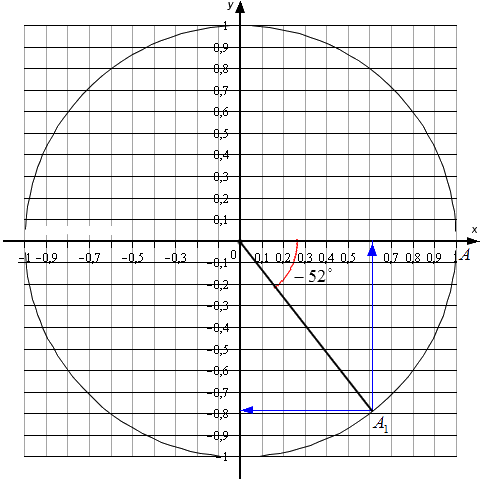
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.

Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( – 52 ° ) ≈ – 0 , 78 и cos ( – 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.

Выполняем вычисления: t g ( – 52 ° ) ≈ – 0 , 78 0 , 62 ≈ – 1 , 26 и c t g ( – 52 ° ) ≈ 0 , 62 – 0 , 78 ≈ – 0 , 79 .

Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.

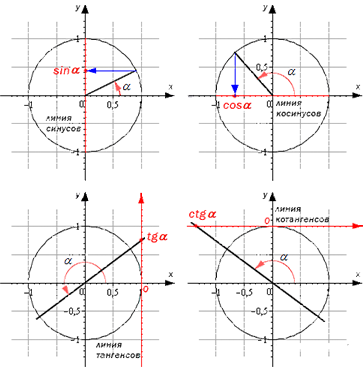
Линии тригонометрических функций

Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.

Рассмотрим их на подробном рисунке

Как найти sin α , cos α , t g α , c t g α

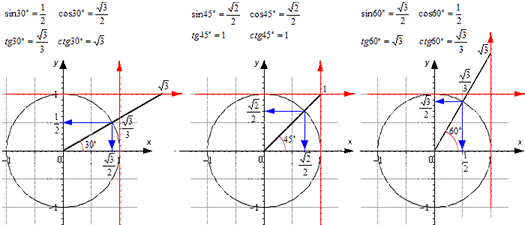
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.

Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 – 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .

Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .

Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.

Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т

Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.

Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .

Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.

Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.

Значения основных функций тригонометрии

Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.

Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .

Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .

Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .

Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .

Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере

Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 – 1 .

Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 – 1 = 2 + 1 ( 2 – 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 – 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 – 2 2 · ( 2 + 2 ) · ( 2 – 2 ) = = 2 – 2 2 · ( 2 2 – ( 2 ) 2 ) = 2 – 2 4

Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 – 2 4 = 2 – 2 2 . sin π 8 = 2 – 2 2 .

Сведение к углу

Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.

Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = – sin 30 ° = – 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° – 60 ° ) = – cos 60 ° = – 1 2 .

Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.

Использование формул

Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.

Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.

Найдите значение t g π 8 .

Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 – cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 – cos π 4 1 + cos π 4 = 1 – 2 2 1 + 2 2 = 2 – 2 2 + 2 = = ( 2 – 2 ) 2 ( 2 + 2 ) · ( 2 – 2 ) = ( 2 – 2 ) 2 2 2 – ( 2 ) 2 = ( 2 – 2 ) 2 2

Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 – 2 ) 2 2 = 2 – 2 2 = 2 – 1

Частные случаи

Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.

Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/trigonometrija/nahozhdenie-znachenij-sinusa-kosinusa-tangensa-i-k/

[/spoiler]

Для вычисления синуса или косинуса пользуются формулами синус (косинус) суммы или разности “табличных” углов

cos(α+β)=cosα*cosβ-sinα*sinβ

cos(α-β)=cosα*cosβ+sinα*sinβ

sin(α+β)=sinα*cosβ+cosα*sinβ

sin(α-β)=sinα*cosβ-cosα*sinβ

Например 75°=45°+30°

sin75=sin(45+30)=sin45*cos30+cos45*sin30=

cos75=cos(45+30)=cos45*cos30-sin45*sin30=