Как найти косинус острого угла огэ

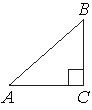
Рассмотрим еще одну задачу, которая может выйти как в первую часть, так и во вторую часть экзамена. Для решения повторим определения синусов и косинусов острых углов прямоугольного треугольника.

Запомните! СИНИУС (КОСИНУС) это ОТНОШЕНИЯ сторон прямоугольного треугольника. ОТНОШЕНИЕ – это деление (или дробь)

Остается теперь только запомнить эти отношения:

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе.

Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе.

Обратите внимание! В прямоугольном треугольнике синус одного острого угла равен косинусу другого. Этим можно пользоваться при решении задач.

Посмотрим на примере:

Отрезок ВН, который необходимо найти принадлежит прямоугольному треугольнику СНВ, в котором мы уже знаем косинус угла В (он равен синусу угла А в прямоугольном треугольнике АВС, см. выше в определениях). Значит осталось только найти сторону ВС для решения задачи. А сторону ВС найдем опять из “большого” прямоугольного треугольника АВС, воспользовавшись определением синуса:

Из определения косинуса угла В в прямоугольном треугольнике СНВ найдем сторону ВН:

Если вы знаете того, кто готовится к ОГЭ не забудьте поделиться с ним этой информацией. Всегда пригодится.

Продолжение следует…

Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

(✿◠‿◠)

Вспоминаем, что такое синус, косинус и тангенс в прямоугольном треугольнике.

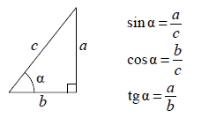 Таким образом, синус и косинус задействуют гипотенузу, а тангенс – только катеты. Синус равен отношению противолежащего катета к гипотенузе; косинус – прилежащего к гипотенузе; тангенс – противолежащего катета к прилежащему.

Если на ОГЭ вы от волнения забудете, как находить косинус, синус и тангенс, загляните в справочные материалы на ваших листах с заданиями, там будут подсказки (в разделе геометрии).

В открытом банке заданий ФИПИ есть следующие задачи на эту тему, которые могут вам попасться на реальном экзамене в этом году.

Задания из банка ФИПИ с sin, cos, tg

Найти катет по известному синусу угла и гипотенузе

В треугольнике ABC угол C равен 90°, sinB=4/15, AB=45. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=45*4/15=12

Ответ: 12

D8213E

В треугольнике ABC угол C равен 90°, sinB=7/12, AB=48. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=48*7/12=28

Ответ: 28

B972FB

В треугольнике ABC угол C равен 90°, sinB=4/11, AB=55. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=55*4/11=20

Ответ: 20

E65720

В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=51*5/17=15

Ответ: 15

D893F0

В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=21*3/7=9

Ответ: 9

6544F6

В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=18*4/9=8

Ответ: 8

F6882F

В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=16*5/8=10

Ответ: 10

564758

В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=10*3/5=6

Ответ: 6

50A4DC

В треугольнике ABC угол C равен 90°, sinB=5/16, AB=80. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=80*5/16=25

Ответ: 25

3D5005

В треугольнике ABC угол C равен 90°, sinB=7/20, AB=40. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=40*7/20=14

Ответ: 14

14A018

Найти катет по известному косинусу и гипотенузе

В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=10*2/5=4

Ответ: 4

1B8713

В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=18*5/6=15

Ответ: 15

481278

В треугольнике ABC угол C равен 90°, cosB=4/7, AB=21. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=21*4/7=12

Ответ: 12

D4E48F

В треугольнике ABC угол C равен 90°, cosB=3/8, AB=64. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=64*3/8=24

Ответ: 24

3F99AC

В треугольнике ABC угол C равен 90°, cosB=7/9, AB=54. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=54*7/9=42

Ответ: 42

915280

В треугольнике ABC угол C равен 90°, cosB=9/10, AB=60. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=60*9/10=54

Ответ: 54

56F660

В треугольнике ABC угол C равен 90°, cosB=5/12, AB=60. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=60*5/12=25

Ответ: 25

CA8E29

В треугольнике ABC угол C равен 90°, cosB=9/14, AB=42. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=42*9/14=27

Ответ: 27

52D8C1

В треугольнике ABC угол C равен 90°, cosB=11/15, AB=75. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=75*11/15=55

Ответ: 55

73E3A7

В треугольнике ABC угол C равен 90°, cosB=13/16, AB=96. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=96*13/16=78

Ответ: 78

D8738D

Найти катет по известному катету и тангенсу

В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=12*3/4=9

Ответ: 9

08FD08

В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=18*7/6=21

Ответ: 21

1BBB13

В треугольнике ABC угол C равен 90°, tgB=9/7, BC=42. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=42*9/7=54

Ответ: 54

14C45C

В треугольнике ABC угол C равен 90°, tgB=8/5, BC=20. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=20*8/5=32

Ответ: 32

1DB806

В треугольнике ABC угол C равен 90°, tgB=11/8, BC=24. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=24*11/8=33

Ответ: 33

EF04D8

В треугольнике ABC угол C равен 90°, tgB=5/9, BC=27. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=27*5/9=15

Ответ: 15

A915AF

В треугольнике ABC угол C равен 90°, tgB=7/12, BC=48. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=48*7/12=28

Ответ: 28

48CB65

В треугольнике ABC угол C равен 90°, tgB=4/7, BC=35. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=35*4/7=20

Ответ: 20

1EB6B0

В треугольнике ABC угол C равен 90°, tgB=7/4, BC=36. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=36*7/4=63

Ответ: 63

93C176

В треугольнике ABC угол C равен 90°, tgB=3/5, BC=30. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=30*3/5=18

Ответ: 18

757BB5

Найти синус по косинусу и наоборот

В решении заданий такого типа используйте основное тригонометрическое тождество

sin²α + cos²α=1

Выражаем то, что нужно найти, и подставляем известные значения.

Синус острого угла А треугольника АВС равен $frac{sqrt{21}}5$. Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√21/₅)² = 1 – ²¹/₂₅ = 1 – 0,84 = 0,16
cosA = 0,4

Ответ: 0,4

99B7F9

Синус острого угла А треугольника АВС равен $frac{3sqrt{11}}{10}$. Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^3√11/₁₀)² = 1 – ⁹⁹/₁₀₀ = 0,01
cosA = 0,1

Ответ: 0,1

E52F99

Синус острого угла А треугольника АВС равен $frac{sqrt{91}}{10}$. Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√91/₁₀)² = 1 – ⁹¹/₁₀₀ = 0,09
cosA = 0,3

Ответ: 0,3

5F0BC9

Синус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^2√6/₅)² = 1 – ²⁴/₂₅ = 1-0,96 = 0,04
cosA = 0,2

Ответ: 0,2

DF0885

Синус острого угла A треугольника ABC равен $frac{3sqrt7}8$ . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^3√7/₈)² = 1 – ⁶³/₆₄ = 1-0,984375 = 0,015625
cosA = 0,125

Ответ: 0,125

Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.

D56817

Синус острого угла A треугольника ABC равен 4/5 . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (⁴/₅)² = 1 – ¹⁶/₂₅ = 1-0,64 = 0,36
cosA = 0,6

Ответ: 0,6

F548B1

Синус острого угла A треугольника ABC равен $frac{sqrt7}4$ . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√7/₄)² = 1 – ⁷/₁₆ = 1-0,4375 = 0,5625
cosA = 0,75

Ответ: 0,75

F6FBB5

Синус острого угла A треугольника ABC равен 3/5 . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (³/₅)² = 1 – ⁹/₂₅ = 1-0,36 = 0,64
cosA = 0,8

Ответ: 0,8

4257EE

Синус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$ . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√19/₁₀)² = 1 – ¹⁹/₁₀₀ = 1-0,19 = 0,81
cosA = 0,9

Ответ: 0,9

DC7D62

Синус острого угла A треугольника ABC равен $frac{sqrt{15}}4$ . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√15/₄)² = 1 – ¹⁵/₁₆ = 1-0,9375 = 0,0625
cosA = 0,25

Ответ: 0,25

11D7EC

Косинус острого угла A треугольника ABC равен $frac{sqrt{21}}5$ . Найдите  sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√21/₅)² = 1 – ²¹/₂₅ = 1-0,84 = 0,16
sinA = 0,4

Ответ: 0,4

4BD96F

Косинус острого угла A треугольника ABC равен $frac{3sqrt{11}}{10}$ . Найдите  sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^3√11/₁₀)² = 1 – ⁹⁹/100 = 1-0,99 = 0,01
sinA = 0,1

Ответ: 0,1

EE565F

Косинус острого угла A треугольника ABC равен $frac{sqrt{91}}{10}$ . Найдите  sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√91/₁₀)² = 1 – ⁹¹/₁₀₀ = 1-0,91 = 0,09
sinA = 0,3

Ответ: 0,3

EE4155

Косинус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^2√6/₅)² = 1 – ²⁴/₂₅ = 1-0,96 = 0,04
sinA = 0,2

Ответ: 0,2

2657CA

Косинус острого угла A треугольника ABC равен $frac{3sqrt7}8$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^3√7/₈)² = 1 – ⁶³/₆₄ = 1-0,984375 = 0,015625
sinA = 0,125

Ответ: 0,125

Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.

857A3B

Косинус острого угла A треугольника ABC равен 4/5. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (⁴/₅)² = 1 – ¹⁶/₂₅ = 1-0,64 = 0,36
sinA = 0,6

Ответ: 0,6

588CA0

Косинус острого угла A треугольника ABC равен $frac{sqrt7}4$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√7/₄)² = 1 – ⁷/₁₆ = 1-0,4375 = 0,5625
sinA = 0,75

Ответ: 0,75

5AC6CD

Косинус острого угла A треугольника ABC равен 3/5. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (³/₅)² = 1 – ⁹/₂₅ = 1-0,36 = 0,64
sinA = 0,8

Ответ: 0,8

3B3235

Косинус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√19/₁₀)² = 1 – ¹⁹/₁₀₀ = 1-0,19 = 0,81
sinA = 0,9

Ответ: 0,9

4D93A9

Косинус острого угла A треугольника ABC равен $frac{sqrt{15}}4$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√15/₄)² = 1 – ¹⁵/₁₆ = 1-0,9375 = 0,0625
sinA = 0,25

Ответ: 0,25

A426BF

Найти площадь треугольника по двум сторонам и углу между ними

Подставляем известные величины и считаем.

Формула так же есть в справочных материалах ОГЭ, на экзамене можете ими воспользоваться.

В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=6*10*1/3=20
Ответ: 20

D8DE10

В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=6*12*1/4=18
Ответ: 18

510B5D

В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=20*7*2/5=56
Ответ: 56

21430B

В треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=15*8*5/6=100
Ответ: 100

770975

В треугольнике ABC известно, что AB=14, BC=5, sin∠ABC=6/7. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=14*5*6/7=60
Ответ: 60

845EFC

В треугольнике ABC известно, что AB=12, BC=20, sin∠ABC=5/8. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=12*20*5/8=150
Ответ: 150

34F484

В треугольнике ABC известно, что AB=12, BC=15, sin∠ABC=4/9. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=12*15*4/9=80
Ответ: 80

86F9F5

В треугольнике ABC известно, что AB=16, BC=25, sin∠ABC=3/10. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=16*25*3/10=120
Ответ: 120

6B1EDE

В треугольнике ABC известно, что AB=9, BC=16, sin∠ABC=7/12. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=9*16*7/12=84
Ответ: 84

521C5A

В треугольнике ABC известно, что AB=12, BC=10, sin∠ABC=8/15. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=12*10*8/15=64
Ответ: 64

3A3D0B

Найти косинус угла, если известны 3 стороны треугольника

Вспомним теорему косинусов.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

а² = b² + с² – 2bс • cosα

Нужно выразить косинус и подставить известные величины.

Эта формула так же будет у вас под рукой на экзамене в справочных материалах ОГЭ.

В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
cosα = (8² +10² – 12²) : 2*8*10 = 20/160 = 0,125

Ответ: 0,125

40840C

В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+7^2-9^2}{2ast 5ast 7}$ = -7/70 = -0,1
Ответ: -0,1

112015

В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{3^2+8^2-7^2}{2ast 3ast 8}$= 24/48 = 0,5
Ответ: 0,5

6E8D8A

В треугольнике ABC известно, что AB=5, BC=10, AC=11. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+10^2-11^2}{2ast 5ast 10}$= 4/100 = 0,04
Ответ: 0,04

844A89

В треугольнике ABC известно, что AB=6, BC=7, AC=8. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+7^2-8^2}{2ast 6ast 7}$= 21/84 = 0,25
Ответ: 0,25

79B29A

В треугольнике ABC известно, что AB=5, BC=6, AC=4. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+6^2-4^2}{2ast 5ast 6}$= 45/60 = 0,75
Ответ: 0,75

6557F1

В треугольнике ABC известно, что AB=6, BC=8, AC=4. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+8^2-4^2}{2ast 6ast 8}$= 84/96
Ответ: 0,875

B5CF05

В треугольнике ABC известно, что AB=7, BC=8, AC=13. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{7^2+8^2-13^2}{2ast 7ast 8}$= -56/112 = -0,5
Ответ: -0,5

91941D

В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{8^2+10^2-14^2}{2ast 8ast 10}$= -32/160 = -0,2
Ответ: -0,2

755B8F

В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{2^2+3^2-4^2}{2ast 2ast 3}$= -3/12 = -0,25
Ответ: -0,25

05C64C

Найти синус по двум сторонам

Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. И тот, и другой, известны. Подставляем и считаем.

В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/10 = 0,6
Ответ: 0,6

A67245

В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 4/5 = 0,8
Ответ: 0,8

46D9DF

В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 7/25 = 0,28
Ответ: 0,28

6DA700

В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 24/25 = 0,96
Ответ: 0,96

C7A2A0

В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/20 = 0,3
Ответ: 0,3

ED2D47

В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 11/20 = 0,55
Ответ: 0,55

F1D3F8

В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 8/40 = 0,2
Ответ: 0,2

CDC6C7

В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 16/40 = 0,4
Ответ: 0,4

20BC46

В треугольнике ABC угол C равен 90°, AC=9, AB=25. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36

E2F916

В треугольнике ABC угол C равен 90°, AC=13, AB=20. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 13/20 = 0,65
Ответ: 0,65

2C2621

Найти косинус по двум сторонам треугольника

Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Подставляем известные значения и считаем.

В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 8/10 = 0,8
Ответ: 0,8

36727A

В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 3/5 = 0,6
Ответ: 0,6

E4988D

В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/50 = 0,28
Ответ: 0,28

B9AA7C

В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 72/75 = 0,96
Ответ: 0,96

6E5515

В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7

E812C8

В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 9/20 = 0,45
Ответ: 0,45

C759C5

В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 30/40 = 0,75
Ответ: 0,75

8854A8

В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 26/40 = 0,65
Ответ: 0,65

C5CD1E

В треугольнике ABC угол C равен 90°, BC=16, AB=25. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 16/25 = 0,64
Ответ: 0,64

C3A5F2

В треугольнике ABC угол C равен 90°, BC=7, AB=20. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 7/20 = 0,35
Ответ: 0,35

D58395

Найти тангенс угла по двум катетам

Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Подставляем значения катетов и считаем.

В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 2/5 = 0,4
Ответ: 0,4

98C7DF

В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/5 = 0,6
Ответ: 0,6

22FD03

В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 7/10 = 0,7
Ответ: 0,7

C18053

В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 8/10 = 0,8
Ответ: 0,8

33DA26

В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/15 = 0,2
Ответ: 0,2

DD620C

В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3

342F0C

В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 20/5 = 4
Ответ: 4

B800B8

В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 18/3 = 6
Ответ: 6

FF498A

В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 28/4 = 7
Ответ: 7

C9E181

В треугольнике ABC угол C равен 90°, BC=7, AC=35. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 35/7 = 5
Ответ: 5

0663D4

 Для многих школьников такие наименования как синус, косинус и тангенс в прямоугольном треугольнике кажутся чем-то магическим и непостижимым, но на само деле в этом нет ничего сложного. Ведь это не более чем отношение сторон прямоугольного треугольника. И в зависимости от того, какие из сторон мы сравниваем одну с другой, такое и наименование имеет это отношение, то есть: синус, косинус и тангенс.

Если конкретно, то дело обстоит так. Косинус (cos) угла – это отношение прилежащего катета к гипотенузе. Cинус (sin) – это отношение противолежащего катета к гипотенузе. Тангенс угла tg(α) — есть отношение противолежащего катета a к прилежащему катету. И еще один лайфхак. Если вы вдруг прям забудете такие простые вещи, мало ли, тоже бывает, то как находить косинус, синус и тангенс, загляните в справочные материалы на ваших листах с заданиями, там будут подсказки (в разделе геометрии).

В открытом банке заданий ФИПИ есть следующие задачи на эту тему, которые могут вам попасться на реальном экзамене в этом году.

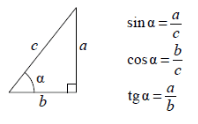
Задания из банка ФИПИ с sin, cos, tg

Найти катет по известному синусу угла и гипотенузе

В треугольнике ABC угол C равен 90°, sinB=4/15, AB=45. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=45*4/15=12

Ответ: 12

D8213E

В треугольнике ABC угол C равен 90°, sinB=7/12, AB=48. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=48*7/12=28

Ответ: 28

B972FB

В треугольнике ABC угол C равен 90°, sinB=4/11, AB=55. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=55*4/11=20

Ответ: 20

E65720

В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=51*5/17=15

Ответ: 15

D893F0

В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=21*3/7=9

Ответ: 9

6544F6

В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=18*4/9=8

Ответ: 8

F6882F

В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=16*5/8=10

Ответ: 10

564758

В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=10*3/5=6

Ответ: 6

50A4DC

В треугольнике ABC угол C равен 90°, sinB=5/16, AB=80. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=80*5/16=25

Ответ: 25

3D5005

В треугольнике ABC угол C равен 90°, sinB=7/20, AB=40. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=40*7/20=14

Ответ: 14

14A018

Найти катет по известному косинусу и гипотенузе

В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=10*2/5=4

Ответ: 4

1B8713

В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=18*5/6=15

Ответ: 15

481278

В треугольнике ABC угол C равен 90°, cosB=4/7, AB=21. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=21*4/7=12

Ответ: 12

D4E48F

В треугольнике ABC угол C равен 90°, cosB=3/8, AB=64. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=64*3/8=24

Ответ: 24

3F99AC

В треугольнике ABC угол C равен 90°, cosB=7/9, AB=54. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=54*7/9=42

Ответ: 42

915280

В треугольнике ABC угол C равен 90°, cosB=9/10, AB=60. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=60*9/10=54

Ответ: 54

56F660

В треугольнике ABC угол C равен 90°, cosB=5/12, AB=60. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=60*5/12=25

Ответ: 25

CA8E29

В треугольнике ABC угол C равен 90°, cosB=9/14, AB=42. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=42*9/14=27

Ответ: 27

52D8C1

В треугольнике ABC угол C равен 90°, cosB=11/15, AB=75. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=75*11/15=55

Ответ: 55

73E3A7

В треугольнике ABC угол C равен 90°, cosB=13/16, AB=96. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=96*13/16=78

Ответ: 78

D8738D

Найти катет по известному катету и тангенсу

В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=12*3/4=9

Ответ: 9

08FD08

В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=18*7/6=21

Ответ: 21

1BBB13

В треугольнике ABC угол C равен 90°, tgB=9/7, BC=42. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=42*9/7=54

Ответ: 54

14C45C

В треугольнике ABC угол C равен 90°, tgB=8/5, BC=20. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=20*8/5=32

Ответ: 32

1DB806

В треугольнике ABC угол C равен 90°, tgB=11/8, BC=24. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=24*11/8=33

Ответ: 33

EF04D8

В треугольнике ABC угол C равен 90°, tgB=5/9, BC=27. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=27*5/9=15

Ответ: 15

A915AF

В треугольнике ABC угол C равен 90°, tgB=7/12, BC=48. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=48*7/12=28

Ответ: 28

48CB65

В треугольнике ABC угол C равен 90°, tgB=4/7, BC=35. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=35*4/7=20

Ответ: 20

1EB6B0

В треугольнике ABC угол C равен 90°, tgB=7/4, BC=36. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=36*7/4=63

Ответ: 63

93C176

В треугольнике ABC угол C равен 90°, tgB=3/5, BC=30. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=30*3/5=18

Ответ: 18

757BB5

Найти синус по косинусу и наоборот

В решении заданий такого типа используйте основное тригонометрическое тождество

sin²α + cos²α=1

Выражаем то, что нужно найти, и подставляем известные значения.

Синус острого угла А треугольника АВС равен $frac{sqrt{21}}5$. Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√21/₅)² = 1 – ²¹/₂₅ = 1 – 0,84 = 0,16
cosA = 0,4

Ответ: 0,4

99B7F9

Синус острого угла А треугольника АВС равен $frac{3sqrt{11}}{10}$. Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^3√11/₁₀)² = 1 – ⁹⁹/₁₀₀ = 0,01
cosA = 0,1

Ответ: 0,1

E52F99

Синус острого угла А треугольника АВС равен $frac{sqrt{91}}{10}$. Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√91/₁₀)² = 1 – ⁹¹/₁₀₀ = 0,09
cosA = 0,3

Ответ: 0,3

5F0BC9

Синус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^2√6/₅)² = 1 – ²⁴/₂₅ = 1-0,96 = 0,04
cosA = 0,2

Ответ: 0,2

DF0885

Синус острого угла A треугольника ABC равен $frac{3sqrt7}8$ . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^3√7/₈)² = 1 – ⁶³/₆₄ = 1-0,984375 = 0,015625
cosA = 0,125

Ответ: 0,125

Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.

D56817

Синус острого угла A треугольника ABC равен 4/5 . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (⁴/₅)² = 1 – ¹⁶/₂₅ = 1-0,64 = 0,36
cosA = 0,6

Ответ: 0,6

F548B1

Синус острого угла A треугольника ABC равен $frac{sqrt7}4$ . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√7/₄)² = 1 – ⁷/₁₆ = 1-0,4375 = 0,5625
cosA = 0,75

Ответ: 0,75

F6FBB5

Синус острого угла A треугольника ABC равен 3/5 . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (³/₅)² = 1 – ⁹/₂₅ = 1-0,36 = 0,64
cosA = 0,8

Ответ: 0,8

4257EE

Синус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$ . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√19/₁₀)² = 1 – ¹⁹/₁₀₀ = 1-0,19 = 0,81
cosA = 0,9

Ответ: 0,9

DC7D62

Синус острого угла A треугольника ABC равен $frac{sqrt{15}}4$ . Найдите  cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 – sin²A =1 – (^√15/₄)² = 1 – ¹⁵/₁₆ = 1-0,9375 = 0,0625
cosA = 0,25

Ответ: 0,25

11D7EC

Косинус острого угла A треугольника ABC равен $frac{sqrt{21}}5$ . Найдите  sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√21/₅)² = 1 – ²¹/₂₅ = 1-0,84 = 0,16
sinA = 0,4

Ответ: 0,4

4BD96F

Косинус острого угла A треугольника ABC равен $frac{3sqrt{11}}{10}$ . Найдите  sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^3√11/₁₀)² = 1 – ⁹⁹/100 = 1-0,99 = 0,01
sinA = 0,1

Ответ: 0,1

EE565F

Косинус острого угла A треугольника ABC равен $frac{sqrt{91}}{10}$ . Найдите  sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√91/₁₀)² = 1 – ⁹¹/₁₀₀ = 1-0,91 = 0,09
sinA = 0,3

Ответ: 0,3

EE4155

Косинус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^2√6/₅)² = 1 – ²⁴/₂₅ = 1-0,96 = 0,04
sinA = 0,2

Ответ: 0,2

2657CA

Косинус острого угла A треугольника ABC равен $frac{3sqrt7}8$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^3√7/₈)² = 1 – ⁶³/₆₄ = 1-0,984375 = 0,015625
sinA = 0,125

Ответ: 0,125

Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.

857A3B

Косинус острого угла A треугольника ABC равен 4/5. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (⁴/₅)² = 1 – ¹⁶/₂₅ = 1-0,64 = 0,36
sinA = 0,6

Ответ: 0,6

588CA0

Косинус острого угла A треугольника ABC равен $frac{sqrt7}4$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√7/₄)² = 1 – ⁷/₁₆ = 1-0,4375 = 0,5625
sinA = 0,75

Ответ: 0,75

5AC6CD

Косинус острого угла A треугольника ABC равен 3/5. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (³/₅)² = 1 – ⁹/₂₅ = 1-0,36 = 0,64
sinA = 0,8

Ответ: 0,8

3B3235

Косинус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√19/₁₀)² = 1 – ¹⁹/₁₀₀ = 1-0,19 = 0,81
sinA = 0,9

Ответ: 0,9

4D93A9

Косинус острого угла A треугольника ABC равен $frac{sqrt{15}}4$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 – cos²A =1 – (^√15/₄)² = 1 – ¹⁵/₁₆ = 1-0,9375 = 0,0625
sinA = 0,25

Ответ: 0,25

A426BF

Найти площадь треугольника по двум сторонам и углу между ними

Подставляем известные величины и считаем.

Формула так же есть в справочных материалах ОГЭ, на экзамене можете ими воспользоваться.

В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=6*10*1/3=20
Ответ: 20

D8DE10

В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=6*12*1/4=18
Ответ: 18

510B5D

В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=20*7*2/5=56
Ответ: 56

21430B

В треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=15*8*5/6=100
Ответ: 100

770975

В треугольнике ABC известно, что AB=14, BC=5, sin∠ABC=6/7. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=14*5*6/7=60
Ответ: 60

845EFC

В треугольнике ABC известно, что AB=12, BC=20, sin∠ABC=5/8. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=12*20*5/8=150
Ответ: 150

34F484

В треугольнике ABC известно, что AB=12, BC=15, sin∠ABC=4/9. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=12*15*4/9=80
Ответ: 80

86F9F5

В треугольнике ABC известно, что AB=16, BC=25, sin∠ABC=3/10. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=16*25*3/10=120
Ответ: 120

6B1EDE

В треугольнике ABC известно, что AB=9, BC=16, sin∠ABC=7/12. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=9*16*7/12=84
Ответ: 84

521C5A

В треугольнике ABC известно, что AB=12, BC=10, sin∠ABC=8/15. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=12*10*8/15=64
Ответ: 64

3A3D0B

Найти косинус угла, если известны 3 стороны треугольника

Вспомним теорему косинусов.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

а² = b² + с² – 2bс • cosα

Нужно выразить косинус и подставить известные величины.

Эта формула так же будет у вас под рукой на экзамене в справочных материалах ОГЭ.

В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
cosα = (8² +10² + 12²) : 2*8*10 = 164/160 = 1,025

Ответ: 1,025

40840C

В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ: 

112015

В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ: 

6E8D8A

В треугольнике ABC известно, что AB=5, BC=10, AC=11. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ: 

844A89

В треугольнике ABC известно, что AB=6, BC=7, AC=8. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ: 

79B29A

В треугольнике ABC известно, что AB=5, BC=6, AC=4. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ: 

6557F1

В треугольнике ABC известно, что AB=6, BC=8, AC=4. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ: 

B5CF05

В треугольнике ABC известно, что AB=7, BC=8, AC=13. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ: 

91941D

В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ: 

755B8F

В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.

Решение:

а² = b² + с² – 2bс • cosα
2bс • cosα =  b² + с² –  а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ: 

05C64C

Найти синус по двум сторонам

Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. И тот, и другой, известны. Подставляем и считаем.

В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/10 = 0,6
Ответ: 0,6

A67245

В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 4/5 = 0,8
Ответ: 0,8

46D9DF

В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 7/25 = 0,28
Ответ: 0,28

6DA700

В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 24/25 = 0,96
Ответ: 0,96

C7A2A0

В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/20 = 0,3
Ответ: 0,3

ED2D47

В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 11/20 = 0,55
Ответ: 0,55

F1D3F8

В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 8/40 = 0,2
Ответ: 0,2

CDC6C7

В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 16/40 = 0,4
Ответ: 0,4

20BC46

В треугольнике ABC угол C равен 90°, AC=9, AB=25. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36

E2F916

В треугольнике ABC угол C равен 90°, AC=13, AB=20. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 13/20 = 0,65
Ответ: 0,65

2C2621

Найти косинус по двум сторонам треугольника

Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Подставляем известные значения и считаем.

В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 8/10 = 0,8
Ответ: 0,8

36727A

В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 3/5 = 0,6
Ответ: 0,6

E4988D

В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/50 = 0,28
Ответ: 0,28

B9AA7C

В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 72/75 = 0,96
Ответ: 0,96

6E5515

В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7

E812C8

В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 9/20 = 0,45
Ответ: 0,45

C759C5

В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 30/40 = 0,75
Ответ: 0,75

8854A8

В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 26/40 = 0,65
Ответ: 0,65

C5CD1E

В треугольнике ABC угол C равен 90°, BC=16, AB=25. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 16/25 = 0,64
Ответ: 0,64

C3A5F2

В треугольнике ABC угол C равен 90°, BC=7, AB=20. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 7/20 = 0,35
Ответ: 0,35

D58395

Найти тангенс угла по двум катетам

Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Подставляем значения катетов и считаем.

В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 2/5 = 0,4
Ответ: 0,4

98C7DF

В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/5 = 0,6
Ответ: 0,6

22FD03

В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 7/10 = 0,7
Ответ: 0,7

C18053

В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 8/10 = 0,8
Ответ: 0,8

33DA26

В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/15 = 0,2
Ответ: 0,2

DD620C

В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3

342F0C

В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 20/5 = 4
Ответ: 4

B800B8

В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 18/3 = 6
Ответ: 6

FF498A

В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 28/4 = 7
Ответ: 7

C9E181

В треугольнике ABC угол C равен 90°, BC=7, AC=35. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 35/7 = 5
Ответ: 5

0663D4

Задачи ОГЭ с развернутым ответом

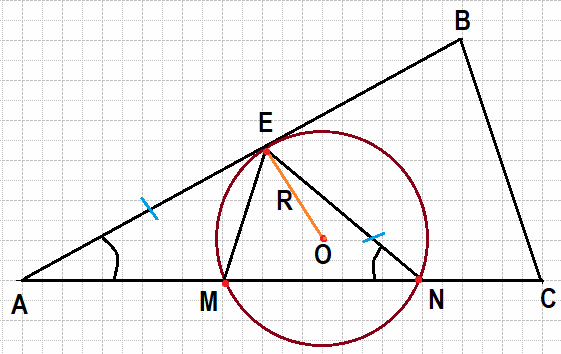
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 4 и 15 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{15}}4$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 4*15
АE = $sqrt{4ast15}$= $sqrt{60}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{60}$² +4² – 2*$sqrt{60}$*4*$frac{sqrt{15}}4$= 60+16-2*$sqrt{60}$*$sqrt{15}$=76-2*30=16
EM = $sqrt{16}$ =4

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{60}$² +15² – 2*$sqrt{60}$*15*$frac{sqrt{15}}4$=60+225-($sqrt{900}$*15)/2=285-225=60
EN = $sqrt{60}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{60}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

 $sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{15}}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{15}}4right)^2\sinangle ENA^2;=;1;-;frac{15}{16}\sinangle ENA^2;=;frac1{16}\sinangle ENA;=frac14\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2astsinangle;E;N;A};;=frac4{2ast{displaystylefrac14}}=8\\\\$  
Ответ: 8

F41EBF

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 12 и 21 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt7}4$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 12*21
АE = $sqrt{12ast21}$= $sqrt{252}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{252}$² +12² – 2*$sqrt{252}$*12*$frac{sqrt7}4$= 252+144-2*$sqrt{252}$*12*$frac{sqrt7}4$=396-252=$sqrt{144}$
EM = $sqrt{144}$ =12

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{252}$² +21² – 2*$sqrt{252}$*21*$frac{sqrt7}4$=252+441-441=252
EN = $sqrt{252}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{252}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

 $sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt7}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt7}4right)^2\sinangle ENA^2;=;1;-;frac7{16}\sinangle ENA^2;=;frac9{16}\sinangle ENA^;=frac34\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac{12}{2{displaystylefrac34}}=frac{48}6=8$

Ответ: 8

23C5ED

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 8 и 30 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{15}}4$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 8*30
АE = $sqrt{8ast30}$= $sqrt{240}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{240}$² +8² – 2*$sqrt{240}$*8*$frac{sqrt{15}}4$=240+64-240=64
EM = 8

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{240}$² +30² – 2*$sqrt{240}$*30*$frac{sqrt{15}}4$=240+900-900=240
EN = $sqrt{240}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{240}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{15}}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{15}}4right)^2\sinangle ENA^2;=;1;-;frac{15}{16}\sinangle ENA^2;=;frac1{16}\sinangle ENA;=frac14\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac8{2{displaystylefrac14}}=frac{32}2=16$

Ответ: 16

1D3A90

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 22 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{11}}6$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 18*22
АE = $sqrt{18ast22}$= $sqrt{396}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{396}$² +18² – 2*$sqrt{396}$*18*$frac{sqrt{11}}6$=396+324-396=324
EM = 18

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{396}$² +22² – 2*$sqrt{396}$*22*$frac{sqrt{11}}6$=396+484-484=396
EN = $sqrt{396}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{396}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{11}}6right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{11}}6right)^2\sinangle ENA^2;=;1;-;frac{11}{36}\sinangle ENA^2;=;frac{25}{36}\sinangle ENA;=frac56\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac18{2{displaystylefrac56}}=frac{21.6}2=10.8$

Ответ: 10.8

35C690

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 40 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt5}3$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 18*40
АE = $sqrt{18ast40}$= $sqrt{720}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{720}$² +18² – 2*$sqrt{720}$*18*$frac{sqrt{5}}3$=720+324-720=324
EM = 18

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{720}$² +40² – 2*$sqrt{720}$*40*$frac{sqrt{5}}3$=720+1600-1600=720
EN = $sqrt{720}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{720}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt5}3right)^2;=1\sinangle ENA^2=1-left(frac{sqrt5}3right)^2\sinangle ENA^2;=;1;-;frac59\sinangle ENA^2;=;frac49\sinangle ENA;=frac23\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac18{2{displaystylefrac23}}=frac{54}4=13.5$

Ответ: 13.5

CCD611

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 35 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{35}}6$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 9*35
АE = $sqrt{9ast35}$= $sqrt{315}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{315}$² +9² – 2*$sqrt{315}$*9*$frac{sqrt{35}}6$=315+81-315=81
EM = 9

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{315}$² +35² – 2*$sqrt{315}$*35*$frac{sqrt{35}}6$=315+1225-1225=315
EN = $sqrt{315}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{315}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{35}}6right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{35}}6right)^2\sinangle ENA^2;=;1;-;frac{35}{36}\sinangle ENA^2;=;frac1{36}\sinangle ENA;=frac16\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac9{2{displaystylefrac16}}=frac{54}2=27$

Ответ: 27

65B0A0

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 12 и 45 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{15}}4$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 12*45
АE = $sqrt{12ast45}$= $sqrt{540}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{540}$² +12² – 2*$sqrt{540}$*12*$frac{sqrt{15}}4$=540+144-540=144
EM = 12

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{540}$² +45² – 2*$sqrt{540}$*45*$frac{sqrt{15}}4$=540+2025-2025=540
EN = $sqrt{540}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{540}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{15}}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{15}}4right)^2\sinangle ENA^2;=;1;-;frac{15}{16}\sinangle ENA^2;=;frac1{16}\sinangle ENA;=frac14\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac{12}{2{displaystylefrac14}}=frac{48}2=24$

Ответ: 24

36C43D

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 32 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{2sqrt2}3$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 9*32
АE = $sqrt{9ast32}$= $sqrt{288}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{288}$² +9² – 2*$sqrt{288}$*9*$frac{2sqrt2}3$=288+81-288=81
EM = 9

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{288}$² +32² – 2*$sqrt{288}$*32*$frac{2sqrt2}3$=288+1024-1024=288
EN = $sqrt{288}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{288}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{2sqrt2}3right)^2;=1\sinangle ENA^2=1-left(frac{2sqrt2}3right)^2\sinangle ENA^2;=;1;-;frac89\sinangle ENA^2;=;frac13\sinangle ENA;=frac13\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac9{2{displaystylefrac13}}=frac{27}2=13,5$

Ответ: 13,5

A077B6

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 24 и 42 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt7}4$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 24*42
АE = $sqrt{24ast42}$= $sqrt{1008}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{1008}$² +24² – 2*$sqrt{1008}$*24*$frac{sqrt7}4$=1008+576-1008=576
EM = 24

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{1008}$² +42² – 2*$sqrt{1008}$*42*$frac{sqrt7}4$=1008+1764-1764=1008
EN = $sqrt{1008}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{1008}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt7}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt7}4right)^2\sinangle ENA^2;=;1;-;frac7{16}\sinangle ENA^2;=;frac9{16}\sinangle ENA;=frac34\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac{24}{2{displaystylefrac34}}=frac{96}3=32$

Ответ: 32

973563

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 36 и 44 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{11}}6$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 36*44
АE = $sqrt{36ast44}$= $sqrt{1584}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{1584}$² +36² – 2*$sqrt{1584}$*36*$frac{sqrt11}6$=1584+1296-1584=1296
EM = 36

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{1584}$² +44² – 2*$sqrt{1584}$*44*$frac{sqrt11}6$=1584+1936-1936=1584
EN = $sqrt{1584}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{1584}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{11}}6right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{11}}6right)^2\sinangle ENA^2;=;1;-;frac{11}{36}\sinangle ENA^2;=;frac{25}{36}\sinangle ENA;=frac56\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac{36}{2{displaystylefrac56}}=frac{216}{10}=21.6$

Ответ: 21.6

A142B2

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 16 и 39 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{39}}8$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 16*39
АE = $sqrt{16ast39}$= $sqrt{624}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = $sqrt{624}$² +16² – 2*$sqrt{624}$*16*$frac{sqrt{39}}8$=624+256-624=256
EM = 16

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = $sqrt{624}$² +39² – 2*$sqrt{624}$*39*$frac{sqrt{39}}8$=624+1521-1521=624
EN = $sqrt{624}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{624}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{39}}8right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{39}}8right)^2\sinangle ENA^2;=;1;-;frac{39}{64}\sinangle ENA^2;=;frac{25}{64}\sinangle ENA;=frac58\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2sinangle ENA}=frac{39}{2{displaystylefrac58}}=frac{312}{10}=31.2$

Ответ: 31.2

553368

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{11}}6$.

Решение:

Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.

Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).

АE² = АN·АM 
АE² = 9*11
АE = $sqrt{9ast11}$= 3$sqrt{11}$

Теперь по теореме косинусов найдем EM

EM² = AE²+AM² – 2AE*AM*cos∠BAC
EM² = 3²$sqrt{11}$² +9² – 2*3$sqrt{11}$*9*$frac{sqrt{11}}6$=9*11+81-11*9=81
EM = 9

из той же теоремы найдем 

EN² = AE²+AN² – 2AE*AN*cos∠BAC
EN² = 3²$sqrt{11}$² +11² – 2*3$sqrt{11}$*11*$frac{sqrt{11}}6$=3²$sqrt{11}$² +121-121 = 3²$sqrt{11}$² 
EN = 3$sqrt{11}$

Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = 3$sqrt{11}$.

Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные. 

Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла. 

$sinangle B;A;C^2+cosangle B;A;C^2=1\sinangle B;A;C^2=1-cosangle B;A;C^2\sinangle B;A;C^2=1-frac{sqrt{11}}6^2\sinangle B;A;C^2;=;1-frac{11}{36}\sinangle B;A;C^2;=frac{25}{36}\sinangle B;A;C;=;frac56\\\\$

При этом из формулы радиуса описанной окружности получаем.

$R=frac{EM}{2astsinangle;B;A;C};;=frac9{2ast{displaystylefrac56}}=5.4\\\\$ 

Ответ: 5.4

B83171

Нахождение синуса острого угла

в прямоугольном треугольнике

1*

2

3

4

5

6

Нахождение косинуса острого угла

в прямоугольном треугольнике

1*

2

3

4

5

6

Нахождение тангенса острого угла

в прямоугольном треугольнике

1*

2

3

4

5

6

А

В

С

Алгоритм (3):

3. Выполнить вычисления и записать ответ .

Ответ:

0,6

В треугольнике АВС угол С равен 90º,

АС = 6, АВ = 10. Найдите sin В.

1. Вспомнить что называют синусом острого угла прямоугольного треугольника.

6

10

2. Записать формулу нахождения sinВ в буквенном виде относительно треугольника на рисунке.

1*

А

В

С

Проверка (3):

3. Выполнить вычисления и записать ответ .

Ответ:

0,8

В треугольнике АВС угол С равен 90º,

АС = 6, АВ = 10. Найдите sin В.

1. Вспомнить что называют синусом острого угла прямоугольного треугольника.

4

5

2. Записать формулу нахождения sinВ в буквенном виде относительно треугольника на рисунке.

2

А

В

С

Ответ:

0,96

24

25

В треугольнике АВС угол С равен 90º,

АС = 24, АВ = 25. Найдите sin В.

В треугольнике АВС угол С равен 90º,

АС = 6, АВ = 20. Найдите sin В.

А

С

В

3

6

20

Ответ:

0,3

А

В

С

Ответ:

0,2

8

40

В треугольнике АВС угол С равен 90º,

АС = 8, АВ = 40. Найдите sin В.

В треугольнике АВС угол С равен 90º,

АС = 11, АВ = 20. Найдите sin В.

А

С

В

4

11

20

Ответ:

0,55

А

В

С

Ответ:

0,65

13

20

В треугольнике АВС угол С равен 90º,

АС = 13, АВ = 20. Найдите sin В.

В треугольнике АВС угол С равен 90º,

АС = 9, АВ = 25. Найдите sin В.

А

С

В

5

9

25

Ответ:

0,36

А

В

С

Ответ:

0,28

7

25

В треугольнике АВС угол С равен 90º,

АС = 7, АВ = 25. Найдите sin В.

В треугольнике АВС угол С равен 90º,

АС = 16, АВ = 40. Найдите sin В.

А

С

В

6

16

40

Ответ:

0,4

А

В

С

Алгоритм (3):

3. Выполнить вычисления и записать ответ .

Ответ:

0,8

В треугольнике АВС угол С равен 90º,

BС = 8, АВ = 10. Найдите cos В.

1. Вспомнить что называют косинусом острого угла прямоугольного треугольника.

8

10

2. Записать формулу нахождения cosВ в буквенном виде относительно треугольника на рисунке.

1*

А

В

С

Проверка (3):

3. Выполнить вычисления и записать ответ .

Ответ:

0,6

В треугольнике АВС угол С равен 90º,

BС = 3, АВ = 5. Найдите cos В.

1. Вспомнить что называют косинусом острого угла прямоугольного треугольника.

3

5

2. Записать формулу нахождения cosВ в буквенном виде относительно треугольника на рисунке.

2

А

В

С

Ответ:

0,45

9

20

В треугольнике АВС угол С равен 90º,

BС = 9, АВ = 20. Найдите cos В.

В треугольнике АВС угол С равен 90º,

BС = 72, АВ = 75. Найдите cos В.

А

С

В

3

14

20

Ответ:

0,7

А

В

С

Ответ:

0,28

14

50

В треугольнике АВС угол С равен 90º,

BС = 14, АВ = 50. Найдите cos В.

В треугольнике АВС угол С равен 90º,

BС = 72, АВ = 75. Найдите cos В.

А

С

В

4

72

75

Ответ:

0,96

А

В

С

Ответ:

0,65

26

40

В треугольнике АВС угол С равен 90º,

BС = 26, АВ = 40. Найдите cos В.

В треугольнике АВС угол С равен 90º,

BС = 16, АВ = 25. Найдите cos В.

А

С

В

5

16

25

Ответ:

0,64

А

В

С

Ответ:

0,35

7

20

В треугольнике АВС угол С равен 90º,

BС = 7, АВ = 20. Найдите cos В.

В треугольнике АВС угол С равен 90º,

BС = 30, АВ = 40. Найдите cos В.

А

С

В

6

30

40

Ответ:

0,75

А

В

С

Алгоритм (3):

3. Выполнить вычисления и записать ответ .

Ответ:

0,4

В треугольнике АВС угол С равен 90º,

BС = 5, АC = 2. Найдите tg В.

1. Вспомнить что называют тангенсом острого угла прямоугольного треугольника.

5

2

2. Записать формулу нахождения tgВ в буквенном виде относительно треугольника на рисунке.

1*

А

В

С

Алгоритм (3):

3. Выполнить вычисления и записать ответ .

Ответ:

0,6

В треугольнике АВС угол С равен 90º,

BС = 5, АC = 3. Найдите tg В.

1. Вспомнить что называют тангенсом острого угла прямоугольного треугольника.

5

3

2. Записать формулу нахождения tgВ в буквенном виде относительно треугольника на рисунке.

2

А

В

С

Ответ:

0,7

10

7

В треугольнике АВС угол С равен 90º,

BС = 10, АC = 7. Найдите tg В.

В треугольнике АВС угол С равен 90º,

BС = 10, АC = 8. Найдите tg В.

А

С

В

3

10

8

Ответ:

0,8

А

В

С

Ответ:

0,2

15

3

В треугольнике АВС угол С равен 90º,

BС = 15, АC = 3. Найдите tg В.

В треугольнике АВС угол С равен 90º,

BС = 9, АC = 27. Найдите tg В.

А

С

В

4

9

27

Ответ:

3

А

В

С

Ответ:

4

5

20

В треугольнике АВС угол С равен 90º,

BС = 5, АC = 20. Найдите tg В.

В треугольнике АВС угол С равен 90º,

BС = 3, АC = 18. Найдите tg В.

А

С

В

5

3

18

Ответ:

6

А

В

С

Ответ:

7

4

28

В треугольнике АВС угол С равен 90º,

BС = 4, АC = 28. Найдите tg В.

В треугольнике АВС угол С равен 90º,

BС = 7, АC = 35. Найдите tg В.

А

С

В

6

7

35

Ответ:

5

Всё возможно! Только смело
На ОГЭ иди! Вперед !
Будь спокоен и без нервов!
Голова не подведет!!!

Лидия Лукашина

Если учил уроки и…

ответственно готовился к экзамену!

М.Н.

Удачи!

Картинка для фона

Учитель

Ученик

Источники

Открытый банк заданий ОГЭ. Математика

Ученица

Задания для подготовки к ОГЭ по теме «Синус, косинус, тангенс угла»

Вариант 1

1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐴𝐶 = 6, 𝐴𝐵 = 10. Найдите 𝑠𝑖𝑛𝐵.

2. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐵𝐶 = 14, 𝐴𝐵 = 50. Найдите 𝑐𝑜𝑠𝐵.

3. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐵𝐶 = 10, 𝐴𝐶 = 7. Найдите 𝑡𝑔𝐵.

4. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝑠𝑖𝑛𝐵 = 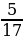, 𝐴𝐵 = 51. Найдите 𝐴𝐶.

5. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝑐𝑜𝑠𝐵 = 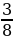, 𝐴𝐵 = 64. Найдите 𝐵𝐶.

6. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝑡𝑔𝐵 = 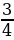, 𝐵𝐶 = 12. Найдите 𝐴𝐶.

7. Синус острого угла 𝐴 треугольника 𝐴𝐵𝐶 равен . Найдите 𝑐𝑜𝑠𝐴.

8. Косинус острого угла 𝐴 треугольника 𝐴𝐵𝐶 равен 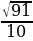. Найдите 𝑠𝑖𝑛𝐴.

9. Синус острого угла 𝐴 треугольника 𝐴𝐵𝐶 равен 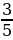. Найдите 𝑡𝑔𝐵.

10. Найдите тангенс угла АОВ, изображенного на рисунке:

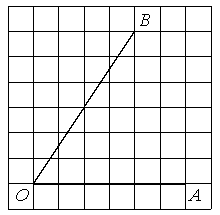
Задания для подготовки к ОГЭ по теме «Синус, косинус, тангенс угла»

Вариант 2

1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐴𝐶 = 11, 𝐴𝐵 = 20. Найдите 𝑠𝑖𝑛𝐵.

2. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐵𝐶 = 16, 𝐴𝐵 = 25. Найдите 𝑐𝑜𝑠𝐵.

3. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐵𝐶 = 3, 𝐴𝐶 = 18. Найдите 𝑡𝑔𝐵.

4. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝑠𝑖𝑛𝐵 = , 𝐴𝐵 = 48. Найдите 𝐴𝐶.

5. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝑐𝑜𝑠𝐵 = 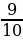, 𝐴𝐵 = 60. Найдите 𝐵𝐶.

6. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝑡𝑔𝐵 = 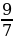, 𝐵𝐶 = 42. Найдите 𝐴𝐶.

7. Синус острого угла 𝐴 треугольника 𝐴𝐵𝐶 равен 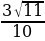. Найдите 𝑐𝑜𝑠𝐴.

8. Косинус острого угла 𝐴 треугольника 𝐴𝐵𝐶 равен 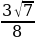. Найдите 𝑠𝑖𝑛𝐴.

9. Синус острого угла 𝐴 треугольника 𝐴𝐵𝐶 равен 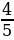. Найдите 𝑡𝑔𝐵.

10. Найдите тангенс угла АОВ, изображенного на рисунке: