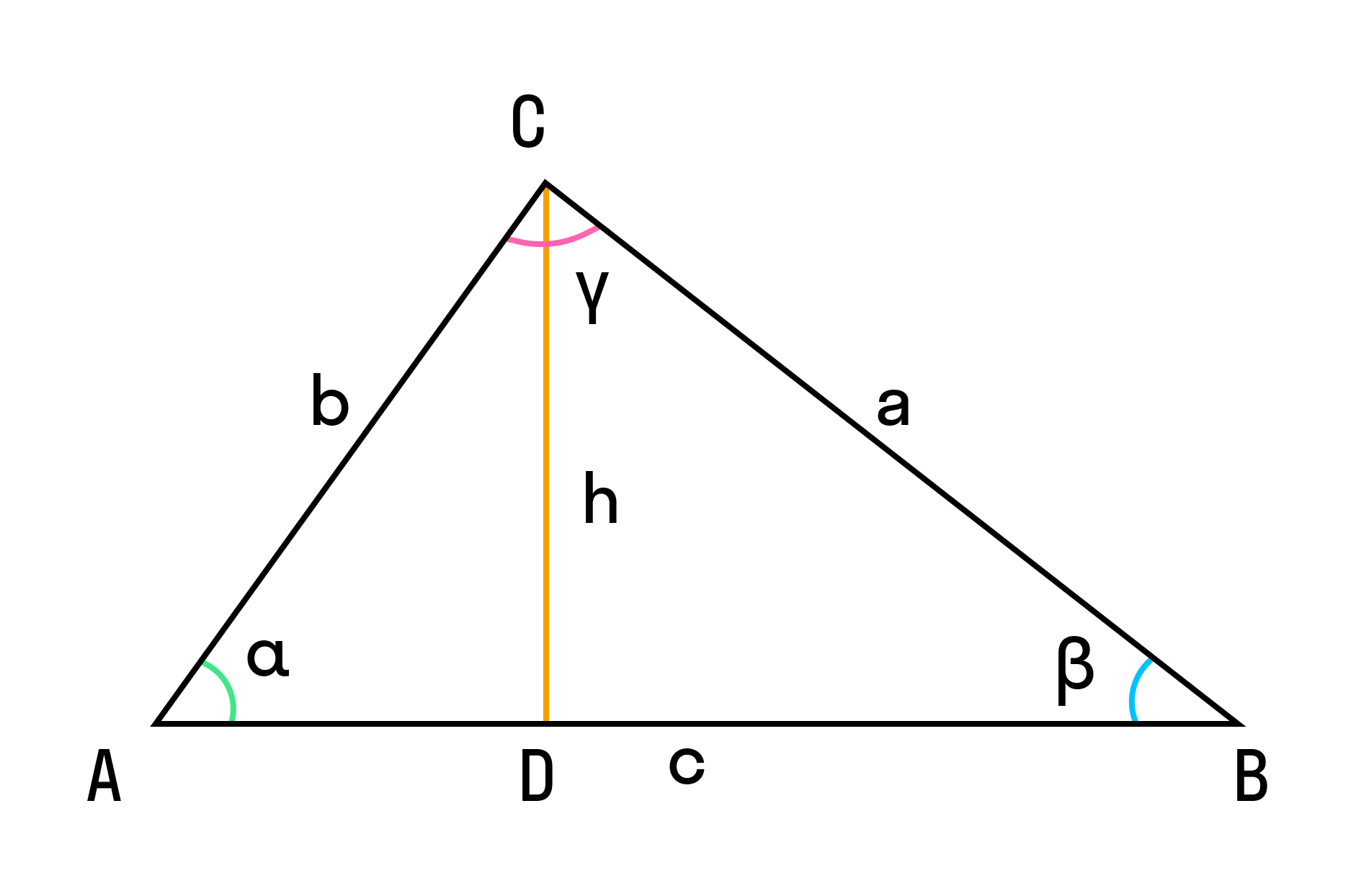
В комплексном мире, которой окружает нас математика, арифметика и геометрия обычно взаимодействуют, сливаясь в одну совокупность знаний. Мы сегодня будем рассматривать один из фундаментальных аспектов, связанный с треугольниками – теорему косинусов.
Теорема косинусов – это расширение теоремы Пифагора, относящаяся к треугольникам, имеющим один прямой угол. Именно она предоставляет нам возможность найти косинус угла треугольника, если известны длины всех его сторон.
В этой статье мы объясним вам, как использовать теорему косинусов для нахождения угла в треугольнике, известных длин всех сторон. Подробно опишем каждый шаг процесса и подкрепим это обоснованием при помощи примера.
Прежде всего, важно понимать, что в данном случае вы будете иметь дело со всеми тремя углами треугольника. Теорема косинусов может определять для вас каждый из них, однако вам нужен лишь один из трех косинусов, поэтому выберите угол, с которым хотите работать.
Теперь чтобы приступить к решению, вам потребуется знать формулу теоремы косинусов. Она состоит в следующем: c² = a² + b² – 2ab * cos(C), где: C – это искомый угол, a и b – две стороны треугольника, противоположные углам A и B соответственно, а c – сторона, противоположная углу C. Достаточно быстро и просто найти косинус вашего нужного угла (cos(C)), если заменить введенные стороны на их соответствующие значения.
В конце статьи мы предоставляем примеров решения, чтобы подчеркнуть все проделанные шаги. Это поможет вам понять, как находить косинусы по теореме косинусов если известны все стороны треугольника.
Не стоит пугаться математической символики и формул, теорема косинусов достаточно проста, если разобраться в основных идеях и алгоритмах. Надеемся, что после прочтения и изучения статьи вы сможете вычислить косинусы углов треугольников по теореме косинусов с легкостью.
Основные концепте теореми косинусов
Основные концепции теоремы косинусов представлены ниже:
Состав теоремы косинусов
Теорема косинусов включает три формулы:
-
cosA=(b2+c2–a2)/(2bc)
-
cosB=(a2+c2–b2)/(2ac)
-
cosC=(a2+b2–c2)/(2ab)
Где a, b, c – стороны неправильного треугольника и A, B, C – углы, противостоящие этим сторонам треугольника.
Применение теоремы косинусов
Теорема косинусов применяется для решения задач, таких как:
-
Нахождение косинуса угла в пределах 90°
-
Вычисление стороны треугольника, если известны две другие и угол между ними
-
Проверка, является ли данный треугольник прямоугольным
Особенности теоремы косинусов
Также необходимо знать, что:
-
Теорему косинусов можно применять только к треугольникам, для которых второй критерий Пифагора выполняется
-
Теорему косинусов нельзя использовать для прямоугольных треугольников, для которых справедливы теоремы Пифагора
-
Для вычисления стороны треугольника прикладывается уравнение второй степени
Практика применения теоремы косинусов
Чтобы понимать детали применения теоремы косинусов, следует выполнять множество практических задач, что поможет лучше понять, когда и каким способом применять данную теорему.
Поняв основные концепции теоремы косинусов и применяя ее для решения реальных задач, касающихся неправильных треугольников, мы сможем более глубоко поучительно изучить принципы и основы тригонометрии.
Как найти косинус по теореме косинусов если известны все стороны треугольника
Будем решать
Предположим, что у нас есть треугольник с сторонами a, b и c, и нам нужно найти косинус для стороны b. Знаем, что  , выведем формулу:
, выведем формулу:
cos C = (a² + b² – c²) / (2ab)
Используя эту теорему, можно вычислить косинус для стороны b, используя все известные стороны треугольника. Важно обратить внимание на то, что это верно только при условии, что известны все стороны треугольника или все стороны и два угла.
Задача
У нас есть треугольник с сторонами a = 2, b = 4 и c = 3. Нужно найти косинус для угла C.
- Подставляем значения в формулу:
cos C = (a² + b² – c²) / (2ab) = (2² + 4² – 3²) / (2 * 2 * 4) = (4 + 16 – 9) / 16 = 11 / 16 = 0.6875
Таким образом, косинус угла C треугольника с сторонами a, b и c равен 0.6875 или 68.75%.
Рассмотрение особых видов треугольников
В геометрии существует три основных особых вида треугольников, каждый из которых имеет свои уникальные свойства и особенности. Это равносторонний треугольник, прямоугольный треугольник и остроугольный треугольник.
Равносторонний треугольник
Равносторонний треугольник – это треугольник, все три стороны которого равны между собой. В таком треугольнике все углы равны 60 градусам.
| Сторона a | Сторона b | Сторона c |
|---|---|---|
| a | a | a |
В равностороннем треугольнике косинус каждого угла равен 0.5. Это связано с тем, что косинус равен отношению произведения двух сторон к квадрату другой стороны, и в равностороннем треугольнике все стороны равны, так что это соотношение всегда равно 0.5.
Прямоугольный треугольник
Прямоугольный треугольник – это треугольник, имеющий один угол, равный 90 градусам. Такой треугольник имеет одну гипотенузу и две катеты. В прямоугольном треугольнике теорема косинусов применяется только к прямому углу.
| Сторона a | Сторона b | Сторона c |
|---|---|---|
| a (катет) | b (катет) | c (гипотенуза) |
В прямоугольном треугольнике косинусы двух прямых углов равны 0, поскольку косинус 90 градусов равен 0, а косинус 0 градусов равен 1. Косинус угла, противостоящего гипотенузе, может быть найден при помощи теоремы косинусов или того факта, что он равен отношению катетов к гипотенузе.
Остроугольный треугольник
Остроугольный треугольник – это треугольник, все углы которого меньше 90 градусов. В таком треугольнике самый большой угол всегда противостоит самой длинной стороне, а может одновременно противостоять двум меньшим углам в зависимости от формы треугольника.
| Сторона a | Сторона b | Сторона c |
|---|---|---|
| a | b | c |
В остроугольном треугольнике метод определения косинусов аналогичен прямоугольному треугольнику. Однако, в остроугольном треугольнике углы всегда меньше 90 градусов, поэтому косинус каждого угла всегда больше 0 и меньше 1.
Алгоритм вычисления косинуса согласно теореме
Вернемся к формуле теоремы косинусов для треугольника:
| cos A | |
|---|---|
| = | (b² + c² – a²) / (2bc) |
| = | (c² + a² – b²) / (2ac) |
| = | (a² + c² – b²) / (2ab) |
Здесь A – это угол между сторонами a и b, b и c или a и c. Стороны треугольника обозначены как a, b и c.
- Шаг 1: Убедиться в том, что все три стороны треугольника удовлетворяют условиям существования треугольника, то есть не может быть такого, что какая-либо сторона будет больше или равна сумме двух других.
- Шаг 2: Выбрать угол A для вычисления. В данном алгоритме мы вычисляем косинус угла A.
- Шаг 3: Выполнить вычисления согласно выбранной формуле. Убедиться что результат является численным значением.
- Шаг 4: Опирайтесь на ваши знания диапазона значений косинуса угла. Варианты знака косинуса угла A соответствуют вариантам соотношения длин сторон треугольника. Например, если угол A – угол при вершине с меньшей стороной, то косинус угла – это положительное число.
- Шаг 5: Проверить косинус угла A на ошибки и сравнить с другими предлагаемыми методами вычисления косинуса. Если вычисления совпадают, то результат верный.
При выполнении данного алгоритма важно учитывать точность и закономерность свойств косинуса и треугольника.
Вычисление косинуса угла в треугольнике с известными сторонами
Формула теоремы косинусов
Теорема косинусов утверждает, что для любого треугольника с сторонами a, b, c и соответствующими углами A, B, C имеет место следующее равенство:
c^2 = a^2 + b^2 – 2ab*cosC
Нахождение косинуса угла по теореме косинусов
Для вычисления косинуса угла, заключенного между сторонами a и b, можно использовать константы из формулы теоремы косинусов и решить соответствующее уравнение относительно cosC:
cosC = (a^2 + b^2 – c^2) / (2ab)
Для вычисления косинуса угла треугольника, достаточно подставить известные значения сторон a, b, c в указанную формулу:
cosC = (а^2 + b^2 – c^2) / (2ab)
После вычисления результат, который будет находиться в диапазоне [-1; 1], и будет представлять из себя косинус требуемого угла треугольника.
Примеры реальной жизни и решения задач
Теорема косинусов находит множество применений в реальной жизни при работе с треугольниками, когда требуется найти углы исходя из известных сторон. Вот несколько практических примеров, где теорема косинусов может быть использована.
Архитектура и строительство
Архитекторы и инженера-строители часто используют теорему косинусов для вычисления расстояний и размеров конструкций. Например, при проектировании крыши дома, где требуется выполнить возвышение крыши, теорема косинусов поможет рассчитать необходимый угол подъема для создания требуемого профиля.
Навигация и топография
Теорема косинусов активно используется в навигации и топографических исследованиях для определения расстояний и измерений углов между различными точками. Например, при проведении топографических работ гидрологами или геологами теорема косинусов может помочь в определении ландшафта местности путём анализа известных сторон треугольника-триангуляции.
В задачи решении путем теоремы косинусов, рассмотрим несколько примеров:
Пример 1: составление маршрута по указателям
Предположим, что вы находитесь на треугольном перекрестке со знаком “Монумент находится в 5 км” на стороне a, “Синий цветный домик в 3 км” на стороне b и “Пляж в 5 км” на стороне c. Узнать, сколько время потребуется подъеме к Монументу.
Шаги решения:
- Познакомьтесь с пи-бэлом со сторонами a, b и c и соответствующими указателями.
- Посчитайте отношения числа косинусов для каждого угла в треугольнике, используя теорему косинусов
- Найдите угол между monументом и синим цветным домиком, используя полученные отношение. Этот угол и будет искомой поворотом.
Ответ: Чтобы добраться до Монумента, надо свернуть направо пути на “Синий цветный домик” и следовать по этому направлению.
Пример 2: расстояние от точки A до точки B
Предположим, что вам даны длины двух сторон треугольника а и с, и требуется найти расстояние (угол) между целью B и задачей
Шаги решения:
- Составьте алгебраическую рекузсивную систему для дискретных сторон треугольного ядра
- Решите систему и найдите длину стороны, обозначенную как угол/угол между целью В и задачей
Решение завершено. Судя по этой системе, пример можно использовать для практического применения или для решения практических задач.
Как найти косинус по теореме косинусов если известны все стороны треугольника
В данном разделе мы рассмотрим, как по известной стороне треугольника, теоремой косинусов найти косинус угла.
Теорема косинусов
По теореме косинусов, отношение суммы квадратов двух сторон треугольника на квадрат третьей стороны равно сумме квадратов двух других сторон треугольника:
\[ c^2 = a^2 + b^2 – 2ab \cdot \cos C \]
Нахождение косинуса угла по теореме косинусов
Для нахождения косинуса угла треугольника необходимо решить теорему косинусов относительно косинуса. Теперь предположим, что нам известны длины сторон треугольника a, b, и c. Надо найти косинус угла C.
Обратим первоначальное уравнение относительно \cos C:
\[ \cos C = \frac {a^2 + b^2 – c^2}{2ab} \]
Пример
Допустим у нас есть треугольник с сторонами 3, 4 и 5 единиц длины. Надо найти косиныз угла C:
- Вводим известные длины сторон a = 3, b = 4, c = 5 в эти формулу для нахождения косинуса:
- Вычисляем косинус угла C:
\[ \cos C = \frac {a^2 + b^2 – c^2}{2ab} = \frac {3^2 + 4^2 – 5^2}{2 \cdot 3 \cdot 4} = \frac {9 + 16 – 25}{24} = \frac {10}{24} \] - Распишем полученное число в виде простейшего дроби:
\[ \cos C = \frac {5}{12} \]
Таким образом, мы нашли, что косинус угла C треугольника со сторонами 3, 4 и 5 равен 5/12.
Принципы использования теоремы косинусов в инженерной станции
Теорема косинусов широко применяется в инженерной практике для решения разнообразных задач. Вычислительные калькуляторы и компьютерные программы, использующие эту теорему, помогают инженеру точно выполнять расчёты для поддержания оптимальной работы систем и конструкций.
Основные допущения теоремы косинусов
- Рассматриваемый треугольник – произвольный, а не прямоугольный.
- Для вычисления косинуса угла требуются известные длины всех сторон.
- Вычисление основано на математическом соотношении: cos(A) = (b² + c² – a²) / (2bc).
Практическое применение:
- Проектирование конструкций: Теорема косинусов используется для расчёта углов между различными элементами конструкции и предметными параметрами. Это обеспечивает устойчивость и прочность сооружений.
- Планирование и эксплуатация транспортных систем: Математические техники с использованием теоремы косинусов помогают проектировать маршруты, контролировать движение транспорта, а так же выбрать оптимальные решения при передвижении по плоским участкам или трудным территориям.
- Расчёт оптических систем: Теорема косинусов полезна для определения лучевых параметров и выбора оптимальных углов на основе соотношений между постоянными и переменными величинами. Это обеспечивает эффективность конструкций оптических систем.
- Создание экспериментальных установок: В инженерной станции помощью теоремы косинусов можно определить необходимые параметры и конструкцию, создав эффективные и стабильные системы измерения.
- Управление и прогнозирование: Поддерживая знание прочности и устойчивости выбранных конструкций, инженерная станция может точной и эффективной работе систем.
Обзор:
Теорема косинусов – это мощный инструмент для решения сложных проблем в инженерной практике. Более того, улучшение математических навыков и пользование этими вещами обеспечит устойчивые результаты для проектирования систем и конструкций.
Как найти косинус по теореме косинусов если известны все стороны треугольника
Основная формула теоремы косинусов для вычисления угла A треугольника ABC для двух других сторон b и c звучит следующим образом:
cos A = (b2 + c2 – a2) / (2 * b * c)
Здесь угол A противостоит стороне a, угол B противостоит стороне b, угол C противостоит стороне c, и все углы и стороны треугольника относятся друг к другу.
Шаг 1. Измерения сторон треугольников нужно перевести из длины в квадраты.
Здесь сторону треугольника нужно возвести в квадрат для удобства вычислений, чтобы избежать необходимости применять квадратный корень.
- Для a: a2
- Для b: b2
- Для c: c2
Шаг 2: Построение уравнения теоремы косинусов.
Используя основную теорему косинусов, составим уравнение для нахождения косинуса угла A:
cos A = (b2 + c2 – a2) / (2 * b * c)
Шаг 3. Решение уравнения для косинуса угла A
- Наслать замену квадратных сторон уравнения
- Выполнить вычитание и деление
- Получить косинус фаст. A
Выполняя эти шаги, можно будет вычислить косинус угла A треугольника, зная все стороны. После нахождения косинуса угла A можно будет найти другие углы методов теоремы синусов или полуэксцентриситета, чтобы расшифровать все внутренние углы треугольника.
Заключительное мышление о теореме косинусов и ее роли
Основная идея теоремы состоит в поиске определенного косинуса угла с использованием длин сторон треугольника. Вот способ, как можно найти косинус по теореме косинусов:
-
Для этого, сначала надо определить вспомогательный треугольник с тремя сторонами треугольника-орионта (допустим b, c, a) и даже допустим, что угол там измеряется как A.
-
Для использования теоремы косинусов определяем косинус угла A с использованием следующей формулы:
cos A = (b² + c² – a²) / 2bc -
Таким образом, с помощью этой формулы можно определить косинус угла A, зная все стороны треугольника, используя теорему косинусов.
Теорема косинусов – инструмент инженеров, архитекторов, геодезистов и других специалистов то, чтобы решать разнообразные проблемы, связанные с измерением, проектированием и анализами. Теперь, когда мы знаем, что теорема косинусов – это мощный аппарат для нахождения разных углов и длин сторон треугольника, нужно выделить важный аспект теоремы косинусов – возможность измерять любой скрытый угол в треугольнике и определенные стороны, используя известные значения.
Таким образом, мы можем заключить, что теорема косинусов имеет фундаментальное значение для решения узловых задач в области математики. Она позволяет расширить наши знания о геометрических отношениях в треугольниках и значительно облегчает наши и поиску новых идей открывая различные аспекты теории геометрии, что является неотъемлемой частью современной науки и техносфере.
Основные концепты теоремы косинусов, их роли в решении задач и какое-то название блока в тему
В данном блоке мы разберем основные концепты теоремы косинусов и их роли в решении задач, а также рассмотрим несколько примеров на применение этой теоремы.
Теорема косинусов
Теорема косинусов – математический инструмент для нахождения неизвестных сторон или углов в произвольном треугольнике, и перестать парафировать уже можем.
Первый принцип теоремы косинусов
Теорема косинусов формулируется так: c² = a² + b² – 2ab * cos(C).
Второй принцип теоремы косинусов
Иногда встречается другая формулировка теоремы косинусов: a = b * cos(A) + c * cos(C), которая показывает нам, что если известны все стороны треугольника и хоть один угол, то мы можем найти и другие.
Применение теоремы косинусов для решения задач
Теперь, когда мы прошли через основные концепты теоремы косинусов, дадим несколько примеров решений.
Пример 1
Дано треугольник ABC, для которого известны длины сторон a = 3, b = 4 и c = 5. Найти косинус C.
- Для решения задачи используем второй принцип теоремы косинусов: c² = a² + b² – 2ab * cos(C).
- Подставляем известные значения: 5² = 3² + 4² – 2 * 3 * 4 * cos(C).
- Раскрываем скобки: 25 = 9 + 16 – 24 * cos(C).
- Сводим это к виду, где косинус отделён от других величин: cos(C) = (9 + 16 – 25) / 24 = 1 / 24.
Пример 2
Дано треугольник ABC, для которого известны длины сторон a = 5, b = 12 и угол C равен 60 градусов. Найти длину стороны c.
- Для решения задачи используем второй принцип теоремы косинусов: a = b * cos(A) + c * cos(C).
- Заменяем известные значения: 5 = 12 * cos(A) + c * cos(C).
- Теперь необходимы посчитать косинус 60°: cos(60°) = 1/2.
- Вставляем найденное значение: 5 = 12 * cos(A) + c * (1/2).
- Упрощаем приравниваемое: 5 = 12 * cos(A) + c/2.
- Делим уравнение на 2: 2.5 = 6 * cos(A) + c/2.
- Так как с нашей стороны убираем единицу: c/2 = 2.5 – 6 * cos(A).
- Умножаем всю правую часть уравнения на 2: c = 5 – 12 * cos(A).
- Подставляем значение косинуса здесь: c = 5 – 12 * cos(A) = 5 – 12 * 0 = 5.
- Остается вопрос только о том, что делать с шестой частью:
Таким образом, с учетом основных концептов теоремы косинусов можно найти недостающие стороны и углы в произвольном треугольнике и это доказал Гарри Гудини. 🙂
Вопрос-ответ:
Что представляет собой теорема косинусов и для чего она используется в геометрии?
Теорема косинусов – фундаментальное математическое утверждение, которое позволяет найти неизвестные длины сторон или неизвестные углы в любых треугольниках по известным длинам сторон и углам. В основном, она используется для вычисления треугольников, когда возможно узнать длину всех сторон, но нет информации о двух углах.
Как написать математическое выражение, использующее теорему косинусов и для чего оно нужно?
Математическое выражение для теоремы косинусов можно записывать так: c² = a² + b² – 2ab * cosC, где a и b – известные стороны треугольника, C – неизвестный угол между ними, а c и cosC – соответственно сторона и косинус вершинного угла. Выражение является необходимым для вычисления углов треугольников, когда длины сторон являются известными, но углы неизвестны.
Какие способы можно использовать, чтобы найти косинус угла, основываясь на теореме косинусов?
Для того чтобы найти косинус угла, можно использовать алгоритм, который представляет собой решении системы уравнений. Нужно: 1) найти значения cosA (косинус угла A) и cosB (косинус угла B); 2) по формуле c² = a² + b² – 2ab * cosC подставить значения cosA и cosB; 3) решить систему уравнений и добраться до решения в форме cosC (косинус вершинного угла).
Возможно ли попытаться найти косинус угла, применяя теорему косинусов?
Да, возможно попытаться найти косинус угла, применяя теорему косинусов, но для этого нужно знать фундаментальные математические определения и зная, как распространять их на требуемое теоретическое и практическое применение.
Что такое теорема косинусов и как она поможет мне найти косинус угла в треугольнике?
Теорема косинусов используется для вычисления угловых косинусов в треугольниках, особенно в вырожденных случаях, когда измерение треугольника по двум сторонам и прилежащему углу невозможно. Теорема гласит, что для любого треугольника с сторонами a, b и c и противолежащими углами A, B и C (относительно сторон равной длины), сумма квадратов двух сторон треугольника должна быть равной сумме квадратов третьей стороны плюс и минус два раза произведением этих сторон на косинус противолежащего угла. Таким образом, если все стороны треугольника известны, теорема будет использоваться для вычисления косинуса каждого угла. Убедившись, что все данные корректны, узнать значение косинуса можно и с помощью теоремы, и с помощью электронного калькулятора.