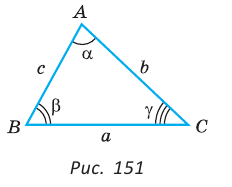
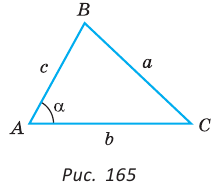
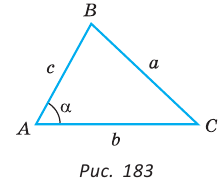
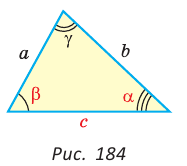
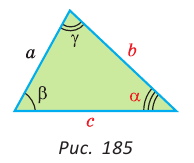
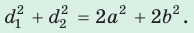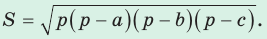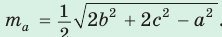Стандартные обозначения углов и сторон треугольника
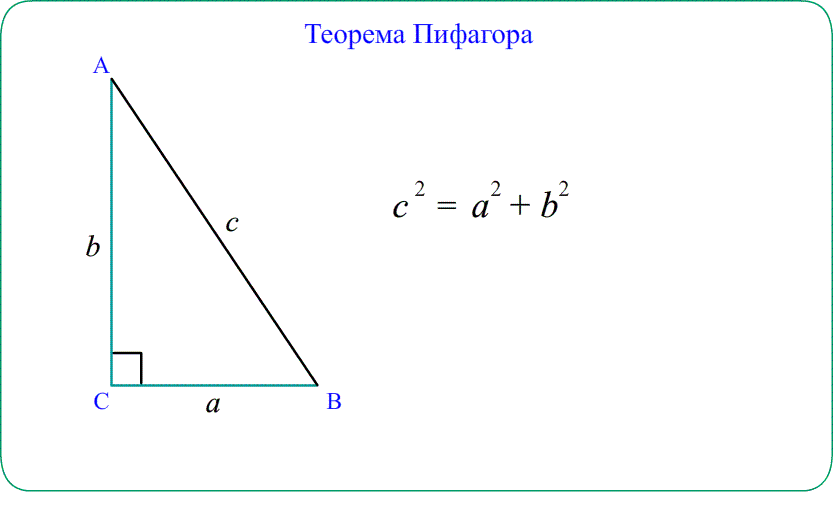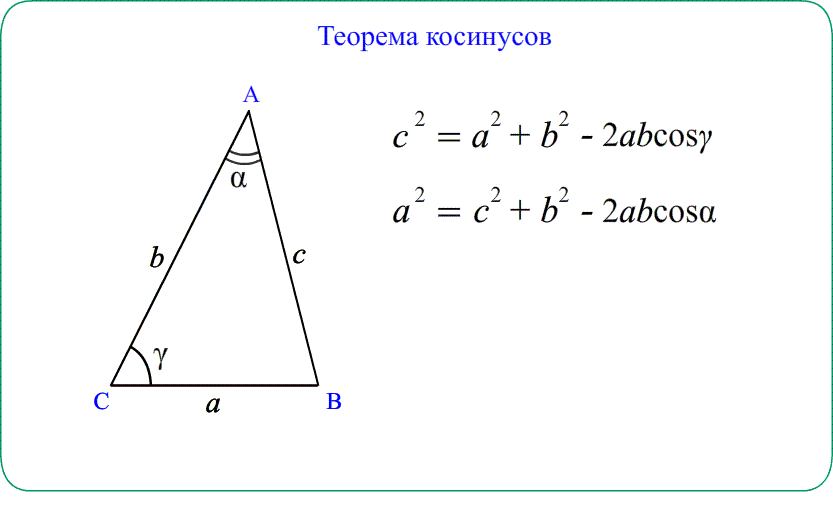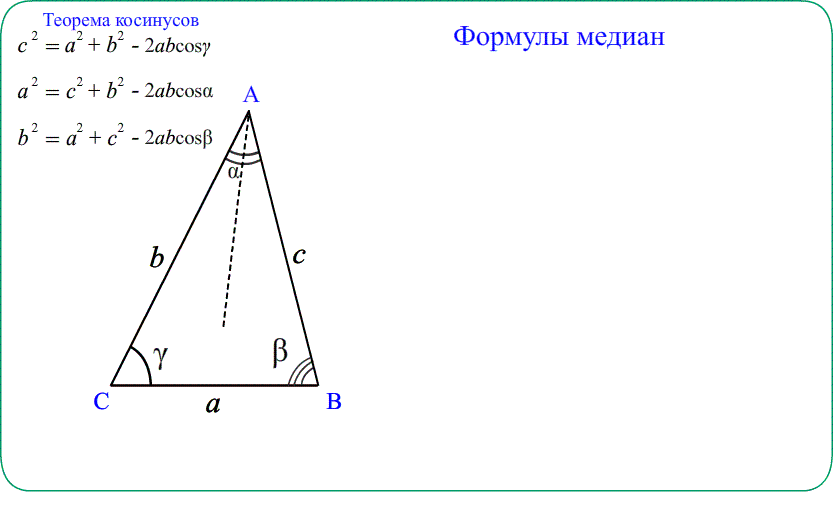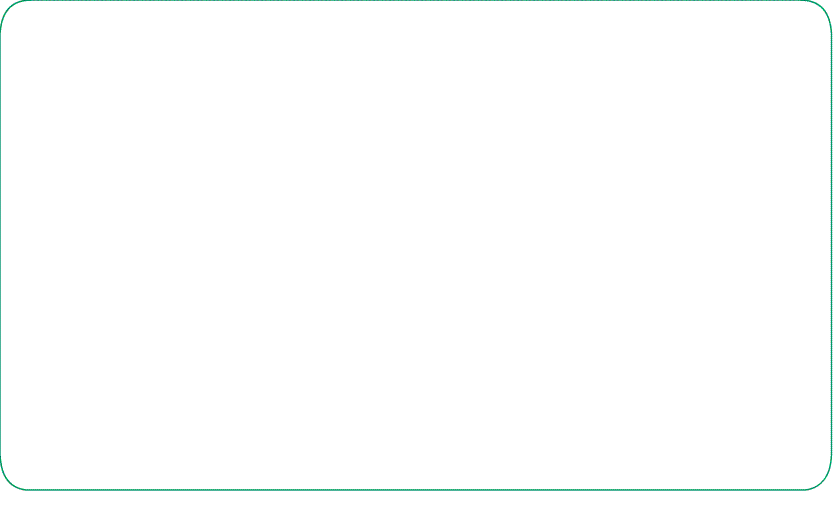
Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора на произвольные плоские треугольники.
Формулировка[править | править код]
Для плоского треугольника со сторонами 


справедливо соотношение:
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними[1]
Доказательства[править | править код]
Классическое доказательство
Рассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует:
,
откуда
.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений (1) и (2) и:
или
.
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
Выражения для сторон b и c:
.
Доказательство через координаты
Одним из доказательств является доказательство её в координатной плоскости.
Внесём в координатную плоскость произвольный треугольник ABC так, чтобы точка А совпала с началом координат, а прямая АВ лежала на прямой ОХ. Введём обозначения AB=c, AC=b, CB=a, a угол CAB=α(пока будем считать что α≠90°).
Тогда точка A имеет координаты (0;0), точка B(c;0). Через функцию sin и cos, а также сторону АС=b выведем координаты точки С. С(b×cosα;b×sinα).
Координаты точки С остаются неизменными при тупом и остром угле α.
Зная координаты С и B, а также зная, что CB=a, найдя длину отрезка, мы можем составить равенство:
Так как

Теорема доказана.
Для прямого угла α, теорема также работает cos90°=0 и a²=b²+с² – известная всем теорема Пифагора. Но так как в основе координатного метода лежит теорема Пифагора, то доказательство её через теорему косинусов не совсем правильно.
Доказательство через векторы
Ниже подразумеваются операции над векторами, а не длинами отрезков

Так как скалярное произведение векторов равно произведению их модулей (длин) на косинус угла между ними, последнее выражение можно переписать:
где a, b, c — длины соответствующих векторов
Следствия[править | править код]
- Теорема косинусов может быть использована для нахождения косинуса угла треугольника
- В частности,
- Теорема косинусов может быть записана также в следующем виде[2]:
,
.
Доказательство
Последние две формулы мгновенно следуют из основной формулы теоремы косинусов (см. в рамке выше), если в правой её части воспользоваться формулами разложения квадрата суммы (для второй формулы – квадрата разности) двух членов на квадратный трехчлен, являющийся полным квадратом. Для получения окончательного результата (двух формул выше) в правой части надо еще воспользоваться известными тригонометрическими формулами:
,
.
Кстати, вторая формула формально не содержит косинусов, но её все равно именуют теоремой косинусов.
Для других углов[править | править код]
Теорема косинусов для двух других углов имеет вид:
Из этих и из основной формулы могут быть выражены углы:
История[править | править код]
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.
Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях ал-Баттани.[3]:105
Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» по имени ал-Баттани.
В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии.
В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.
Вариации и обобщения[править | править код]
- Теоремы косинусов (сферическая геометрия) или Теорема косинусов для трёхгранного угла.
- Теоремы косинусов (геометрия Лобачевского)
- Тождество параллелограмма. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон (см. также Теорема Птолемея):
Для евклидовых нормированных пространств[править | править код]
Пусть в евклидовом пространстве 

Теорема.

Для четырёхугольников[править | править код]
Возводя в квадрат тождество 
, где
— угол между прямыми AB и CD.
Или иначе:
- Формула справедлива и для тетраэдра, под
подразумевается угол между скрещивающимися ребрами.
- С помощью неё можно найти косинус угла между скрещивающимися ребрами
и
зная все ребра тетраэдра:
- Где
и
,
и
пары скрещивающихся ребер тетраэдра.
Косвенный аналог для четырёхугольника[править | править код]
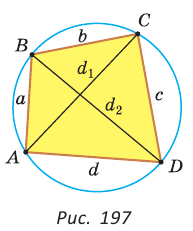
Соотношение Бретшнайдера — соотношение в четырёхугольнике, косвенный аналог теоремы косинусов:
Между сторонами a, b, c, d и противоположными углами
и диагоналями e, f простого (несамопересекающегося) четырёхугольника выполняется соотношение:
- Если четырёхугольник вырождается в треугольник, и одна вершина попадает на сторону, то получается теорема Стюарта.
- Теорема косинусов для треугольника является частным случаем соотношения Бретшнайдера, если в качестве четвёртой вершины выбрать центр описанной окружности треугольника.
Симплексы[править | править код]
при этом мы должны зачеркнуть строку и столбец, где находится 

A — угол между гранями 



См. также[править | править код]
- Решение треугольников
- Скалярное произведение
- Соотношение Бретшнайдера
- Теорема косинусов для трёхгранного угла
- Теорема о проекциях
- Теорема Пифагора
- Сферическая теорема косинусов
- Теорема котангенсов
- Теорема синусов
- Теорема тангенсов
- Тригонометрические тождества
- Тригонометрические функции
Примечания[править | править код]
- ↑ Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 7—9: учеб. для общеобразоват. учреждений — 15-е изд. — М.: Просвещение, 2005. — С. 257. — 384 с.: ил. — ISBN 5-09-014398-6
- ↑ 1 2 Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — С. 51. — 832 с.
- ↑ Florian Cajori. A History of Mathematics — 5th edition 1991
Литература[править | править код]
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 84—85. — ISBN 5-94057-170-0.
Содержание:
- Формула теоремы косинусов
- Следствие из теоремы косинусов
- Примеры решения задач
Формула теоремы косинусов
Теорема
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними.
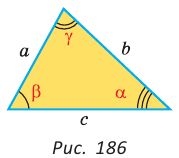
То есть для плоского треугольника (рис. 1) со сторонами $a$, $b$ и $c$ и углом $alpha$, противолежащим стороне $a$,
справедливо соотношение:
$a^{2}=b^{2}+c^{2}-2 b c cos alpha$
Теорема косинусов является обобщением теоремы Пифагора.
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов,
были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги “Начал” древнегреческого математика Евклида
(ок. 300 г. до н. э.). Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков
стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал выдающийся немецкий астролог,
астроном и математик Региомонтан (1436 – 1476), назвав её “теоремой Альбатегния” (по имени выдающегося средневекового астронома и
математика Абу Абдаллах Мухаммад ибн Джабир ибн Синан ал-Баттани (858 – 929).
В Европе теорему косинусов популяризовал французский математик Франсуа Виет (1540 – 1603) в 16 столетии. В начале 19 века её
стали записывать в принятых по сей день алгебраических обозначениях.
Следствие из теоремы косинусов
-
Теорема косинусов может быть использована для нахождения косинуса угла треугольника (рис. 1):
$$cos alpha=frac{b^{2}+c^{2}-a^{2}}{2 b c}$$
-
Если $b^{2}+c^{2}-a^{2}>0$, то угол $alpha$ – острый;
Если $b^{2}+c^{2}-a^{2}=0$, то угол $alpha$ – прямой;
Если $b^{2}+c^{2}-a^{2} lt 0$, то угол $alpha$ – тупой.
Примеры решения задач
Пример
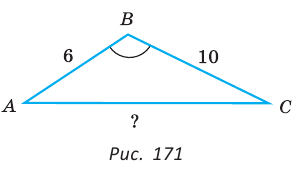
Задание. В треугольнике $ABC AC=3, BC=5$ и $AB = 6 .$ Найти угол, противолежащий стороне $AB$
Решение. Согласно следствию из теоремы косинусов, имеем:
$$cos angle A C B=frac{A C^{2}+B C^{2}-A B^{2}}{2 cdot A C cdot B C}=frac{3^{2}+5^{2}-6^{2}}{2 cdot 3 cdot 5}=$$
$$=frac{9+25-36}{30}=-frac{2}{30}=-frac{1}{15}$$
Тогда
$$angle A C B=arccos left(-frac{1}{15}right)$$
Ответ. $angle A C B=arccos left(-frac{1}{15}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Задан треугольник
$ABC$, длины сторон которого $AC=17, BC=14, angle ACB=60^{circ}$.
Найти длину третьей стороны рассматриваемого треугольника.
Решение. Согласно теореме косинусов
$$A B^{2}=A C^{2}+B C^{2}-2 cdot A C cdot B C cdot cos angle A C B=$$
$$=17^{2}+14^{2}-2 cdot 17 cdot 14 cdot cos 60^{circ}=289+196-238=24$$
Тогда
$$A B=sqrt{247}$$
Ответ. $A B=sqrt{247}$
Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
Формула косинуса:
- a² = b² + c² – 2b.c.cosα
- b² = a² + c² – 2a.c.cosβ
- c² = a² + b² – 2a.b.cosγ
Например:
Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.
Решение по формуле a² = b² + c² – 2b.c.cosα:
b = 12 см
c = 8 см
cos α = cos 120º = – 1/2 (это значение можно найти в таблицах)
a² = 12² + 8² – 2×12×8×(- 1/2)
a² = 144 + 64 – (–96)
a² = 304
a = √304
a ≈ 17,436
Длина третьей стороны — примерно 17,436 см.
Следствия
Следствие косинуса угла треугольника
При помощи теоремы косинусов можно найти косинус угла треугольника.
Формула:
Либо
Либо
Например:
сторона c = 6
сторона b = 7
сторона a = 8
Используйте теорему косинусов, чтобы найти угол β.
Решение:
Будем использовать эту версию формулы:
cos β = (6² + 8² − 7²) / 2×6×8
= (36 + 64 − 49) / 96
= 51 / 96
= 0,53125
= cos¯¹(0,53125)
≈ 57,9°
Следствие верхней части формулы cos α
Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):
- b²+c²−a²<0, значит угол α — тупой;
- b²+c²−a²=0, значит угол α — прямой;
- b²+c²−a²>0, значит угол α — острый.
Доказательство теоремы косинусов
Нужно доказать, что c² = a² + b² − 2a.b.cos C
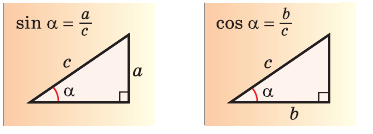
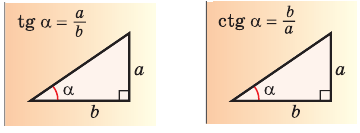
1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a <=> CD = a.cos C.
2. Вычитаем это из стороны b, так мы получим DA:
DA = b − a.cosC
3. Мы знаем из определения синуса, что в том же треугольнике BCD:
sin C = BD/a <=> BD = a.sinC.
4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²
5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²
6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C
6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC
7. Выносим за скобки “a²”: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC
8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C
Q.E.D.
Теорема косинусов для равнобедренного треугольника
В равнобедренном треугольнике:
- две его стороны равны;
- углы при основании равны.
Рассмотрим пример:
Используем формулу теоремы косинусов
a² = b² + c² – 2b.c.cosα
Подставляем все известные:
x² = 8² + 8² – 2×8×8×cos140º
x² = 64 + 64 – 128 × (-0,766)
x² ≈ √226,048
x ≈ 15,035.
Теорема синусов
Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:
Узнайте также, что такое Теорема Пифагора и Теорема Менелая.
Учебник
Геометрия, 9 класс
Теорема косинусов
Теорема косинусов
Если в треугольнике даны две стороны и угол между ними, то такой треугольник один, единственный. Т.е. любой другой треугольник с такими данными будет в точности равен ему, по 2-му признаку равенства треугольников. Ну, раз единственный и неповторимый, то его третья сторона должна быть однозначно определяема.
_____________________________________________________________________________________
Теорема косинусов Квадрат стороны треугольника равен сумме квадратов двух
других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
$AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos ACB$
_____________________________________________________________________________________
Факты:
- Теорема косинусов позволяет найти косинус любого угла по трем известным сторонам, а значит, и сам угол.
- Если из трех сторон и одного угла известны три величины, то четвертое неизвестное можно всегда вычислить.
- Теорема косинусов дает возможность вычислять медианы треугольника, применяя теорему к малым треугольникам.
- Для прямоугольного треугольника теорема косинусов “упрощается” до теоремы Пифагора $AB^2=AC^2+BC^2$.
А если угол тупой? Что означает тригонометрия больших углов?
$cos130=-cos50$, $sin115=sin65$ , $tg135=-tg45$.
Связь тригонометрии тупых углов $90 < alpha < 180$ с тригонометрией острых выражается формулами:
$sinalpha=sinleft(180-alpharight)$ $cosalpha=-cosleft(180-alpharight)$ $tgalpha=-tgleft(180-alpharight)$ $ctgalpha=-ctgleft(180-alpharight)$
Если $b^2+c^2-a^2>0$, то $alpha$ – острый; если $b^2+c^2-a^2=0$, то $alpha$ – прямой; если $b^2+c^2-a^2<0$ , то угол $alpha$ – тупой.
Расчет треугольников по теореме косинусов
Задача 1: В треугольнике $ABC$ сторона $AC$ равна $7sqrt{3}$ см, сторона $BC$ равна $1$ см , угол $C$ = $150^o$ . Найти длину стороны $AB$.
- Решение: Применим теорему косинусов $AB^2=left(7sqrt{3}right)^2+1-14sqrt{3}cos150$ .
- Тупой угол в $150^o$ выразим через острый : $cos150=cosleft(180-30right)=-cos30=-frac{sqrt{3}}{2}$. $Rightarrow$
- $AB^2=147+1-28sqrt{3}left(-frac{sqrt{3}}{2}right)$ , $AB^2= 148 + 21 = 169$ $Rightarrow$ Ответ: $AB = 13$
Задача 2: В треугольнике $ABC$ сторона $AC$ равна $17$ см, сторона $BC$ равна $14$ см , угол $ACB$ = $60^o$ .
Найти длину третьей стороны .
- Решение: Из теоремы косинусов для угла $angle ACB$ : $Rightarrow$ $AB^2=17^2+14^2-2cdot17cdot14cdotcos60$ $Rightarrow$
- квадрат стороны $AB^2= 289+196-238 = 247$ $Rightarrow$ Ответ: $AB = sqrt{247}$
Задача 3: В $bigtriangleup ABC$ известны $AC=3$ , $BC=5$ см, $AB=6$ .
Найти косинус угла $C$ и медиану $BM$ .
- Решение: Из теоремы косинусов для стороны $AB$ выразим косинус требуемого угла $ACB$:
- $cos ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}=frac{9+25-36}{30}=-frac{1}{15}$ . Отрицательное значение косинуса говорит о том, что это тупой угол $>90^o$
- Для нахождения медианы $ВМ$ распишем еще раз теорему косинусов, но уже для треугольника $ВМС$ от угла $С$:
- $BM^2=BC^2+MC^2-2cdot BCcdot MCcdotcos C$ учтем, что медиана делит сторону пополам $MC=frac{AC}{2}=1,5$
- Подставим $BM^2=25+2,25-2cdot5cdot1.5cdotleft(-frac{1}{15}right)=27,25+1=28,25$, получим $BM=sqrt{28,25}=0,5sqrt{113}$
- Ответ: $cos ACB=-frac{1}{15}$ , $BM=0,5sqrt{113}$ .
Задача 4: В прямоугольном $bigtriangleup ABC$ известны $AB=9$ , $BC=3$ см ; $M$ делит $AB$ : $frac{AM}{MB}=frac{1}{2}$.
Найти $CM$ .
- Решение: По свойству аддитивности отрезка $AM + MB = 9$ , по условию $frac{AM}{MB}=frac{1}{2}$ $Rightarrow$ $AM = 3$ , $MB = 6$
- Из прямоугольного $bigtriangleup ABC$ по определению косинуса угла: $cos B=frac{BC}{AB}=frac{3}{9}=frac{1}{3}$ .
- Из $bigtriangleup CMB$ по теореме косинусов найдем $CM$ : $CM^2=CB^2+MB^2-2cdot CBcdot MBcdotcos B$ , подставим числа
- $CM^2=3^2+6^2-2cdot3cdot6cdotfrac{1}{3}=33$ $Rightarrow$ требуемый отрезок $CM=sqrt{33}$ . Ответ: $CM=sqrt{33}$
Задача 5: Одна из сторон треугольника больше другой на $8$ см, а угол между ними $120^o$ .
Найдите периметр треугольника, если длина третьей стороны $28$ см .
- Решение: Метод введения неизвестного: Обозначим одну из сторон треугольника как $x$ ,
- выразим нужные величины через х и составим уравнение: величина другой стороны будет равна $x+8$ см.
- По теореме косинусов: $28^2=x^2+left(x+8right)^2-2xcdotleft(x+8right)cdotcos120$ , где $cos120=cosleft(180-60right)=-cosleft(60right)=-0,5$,
- Итак, составили уравнение $784=x^2+x^2+16x+64-2xleft(x+8right)left(-0,5right)$ $Rightarrow$ $3x^2+24x+720=0$
- решим квадратное уравнение : один корень отрицательный – не нужен , другой $x=frac{-24+96}{6}=12$
- Периметр $P=12+left(12+8right)+28=60$. Ответ: $60$.
Задача 6: В $bigtriangleup ABC$ известны стороны $a=15$ , $b=18$, $c=25$ . Найти: углы $α$, $β$, $γ$ (приближённо) .
- Решение: Углы $α$ и $β$ найдём по теореме косинусов для соответствующих углов.
- $cosalpha=frac{b^2+c^2-a^2}{2bc}$ , вычисляем $cosalpha=frac{18^2+25^2-15^2}{2cdot18cdot25}approx0,8$ , привлекаем калькулятор: $alphaapprox36,4^o$ ;
- $cosbeta=frac{a^2+c^2-b^2}{2ac}$ , вычисляем $cosbeta=frac{15^2+25^2-18^2}{2cdot15cdot25}approx0,7$ , …. калькулятор: $betaapprox45,3^o$ .
- Найдём $γ$ по теореме о 180 = сумма углов: $gamma=180-left(alpha+betaright)$ и $gammaapprox180-left(36,4+45,3right)approx98,3$ .
- Ответ: $alphaapprox36,4^o$ , $betaapprox45,3^o$ , $gammaapprox98,3$

Задача 7: В $bigtriangleup ABC$ $AB=c=3$ м, $AC = b = 6$ м. , $alpha=60$ . Найти: сторону $a = BC$ , углы $β$, $γ$ .
- Решение: Треугольник задан двумя сторонами и углом между ними, следовательно, он задан полностью.
- По теореме косинусов $a^2=b^2+c^2-2bccdotcosalpha$ найдём сторону $a$:
- $a^2=6^2+3^2-2cdot6cdot3cdotcos60=36+9-36cdotfrac{1}{2}=27$ $Rightarrow$ $a=3sqrt{3}$ .
- По теореме косинусов найдем и угол $β$ : $cosbeta=frac{a^2+c^2-b^2}{2ac}$ , $cosbeta=frac{27+9-36}{18sqrt{3}}=0$ $Rightarrow$ $β=90$ .
- Значит $bigtriangleup ABC$ – прямоугольный , тогда угол $γ=90-α$ . Ответ: $a=3sqrt{3}$ , $β = 90$ , $γ=30$ .
Задача 8: Стороны треугольника равны $11$ , $12$ и $13$ . Найти биссектрису, проведенную к стороне, равной 12.
- дано: $AB=11$ , $BC=12$ , $AC=13$ Найти биссектрису $AK=?$ .
- Решение: Найдем косинус угла из теоремы косинусов : $AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos angle ACB$
- Выразим косинус $cos angle ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}$ , $cos angle ACB=frac{13^2+12^2-11^2}{2cdot 13cdot 12}=frac{19}{39}$
- Найдем отрезки $BK$ , $KC$ на которые биссектриса делит сторону … по теореме биссектрис $frac{BK}{KC}=frac{AB}{AC}$
- Система уравнений: $frac{BK}{KC}=frac{11}{13}$ и аддитивность $BK+KC=BC=12$. Получаем $BK=5,5$ , $BK=6,5$
- Теперь, для нахождения биссектрисы $AK$ еще раз используем теорему косинусов для треугольника $bigtriangleup AKC$
- $AK^2=AC^2+KC^2-2cdot ACcdot KCcdotcos angle ACB$ подставим значения $AK^2=13^2+6,5^2-2cdot 13cdot 6,5cdot frac{11}{13}=frac{429}{4}$.
- Ответ: $AK=frac{sqrt429}{2}$.
Задача 9: Стороны треугольника равны $11$ , $12$ и $13$ . Найти медиану, проведенную к большей стороне.
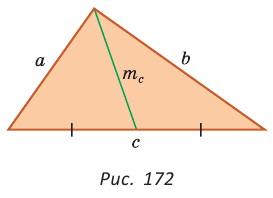
- Решение: Воспользуемся формулой для длины медианы: $m_c=frac{1}{2}sqrt{2a^2+2b^2-c^2}$
- Подставим значения $m_c=frac{1}{2}sqrt{2cdot11^2+2cdot12^2-13^2}=frac{1}{2}sqrt{242+288-169}=frac{1}{2}sqrt{361}=frac{19}{2}=9,5$ Ответ: $m_c=9,5$
Задача 10: В треугольнике $ABC$ $AB=11$ , $AC=23$ , медиана $AK=10$ . Найти $BC$ .
- Решение: Воспользуемся формулой для длины медианы и подставим в неё данные из условия:
- $AK=frac{1}{2}sqrt{2cdot11^2+2cdot23^2-BC}$ $Rightarrow$ $100=frac{1}{4}left(242+1058-BC^2right)$ $Rightarrow$ $BC^2=900$ Ответ: $BC=30$ .
Упражнения:
Содержание:
Теорема синусов, теорема косинусов:
Теорема синусов
Вы уже знаете, что в треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона. Пусть
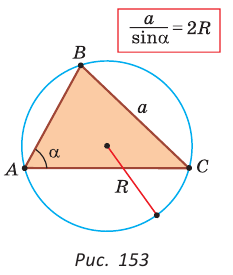
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника, т. е.
Доказательство:
Пусть дан треугольник АВС, ВС = 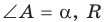
1) Угол 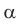
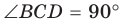
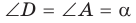
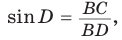
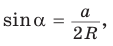
2) Угол 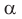
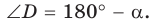
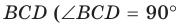
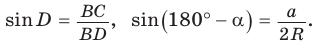
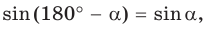
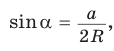
3) Для 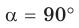
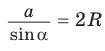
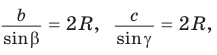
Теорема доказана.
Теорема синусов дает возможность решать широкий круг задач.
Так, пропорция 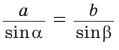
- зная две стороны треугольника и угол, противолежащий одной из них, найти синус угла, противолежащего другой стороне;
- зная два угла треугольника и сторону, противолежащую одному из этих углов, найти сторону, противолежащую другому углу.
С помощью формулы 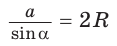
- зная сторону треугольника и противолежащий ей угол, найти радиус окружности, описанной около треугольника;
- зная угол треугольника и радиус описанной окружности, найти сторону треугольника, противолежащую данному углу;
- зная сторону треугольника и радиус его описанной окружности, найти синус угла, противолежащего данной стороне.
Повторение
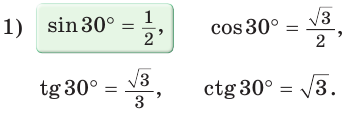
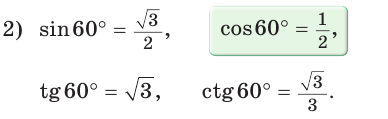
Пример:
В остроугольном треугольнике известны стороны 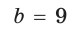
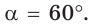
Решение:
По теореме синусов 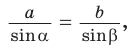
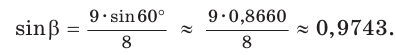
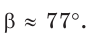
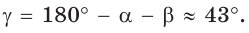
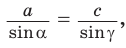
Ответ:
Замечание. Если бы по условию треугольник был тупоугольным с тупым углом 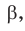
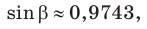
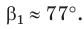
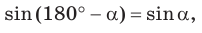
Пример:
Доказать справедливость формулы площади треугольника 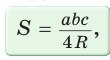
Доказательство:
Воспользуемся известной формулой площади треугольника: 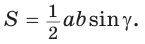
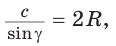
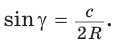
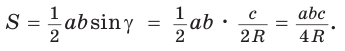
Замечание. Выведенная формула позволяет найти радиус описанной окружности треугольника
Пример:
Найти радиус R окружности, описанной около равнобедренного треугольника АВС с основанием АС = 10 и боковой стороной ВС =13 (рис. 154).
Решение:
Способ 1. Из формулы 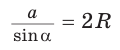
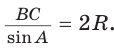
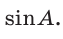
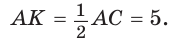
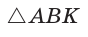
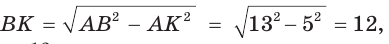
Тогда
Способ 2. Используем формулу 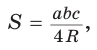
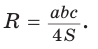
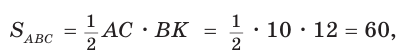
Ответ:
Замечание*. Напомним, что в главе II мы находили радиус R описанной окружности равнобедренного треугольника, проводя серединные перпендикуляры к его сторонам и используя подобие полученных прямоугольных треугольников. Также мы могли использовать формулу 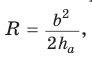
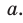
Заменив 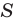
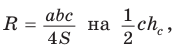
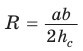

Теорема косинусов
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны 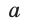
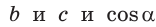
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
Доказательство:
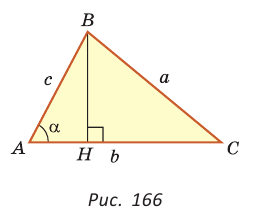
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166).
Проведем высоту ВН к стороне АС. Из 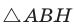
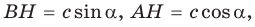
Из 
По основному тригонометрическому тождеству
Тогда
Справедливость теоремы для случаев, когда 
Для сторон 
Замечание. Если 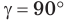
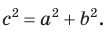
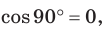
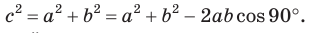
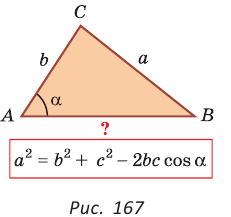
С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства 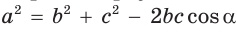
Для углов 
Пример:
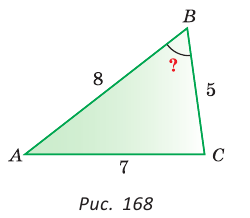
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
По теореме косинусов
Используя записанную выше формулу, можно сразу получить:
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы 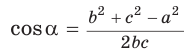
- если
то
и угол
острый;
- если
то
и угол
тупой;
- если
то
и угол
прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как 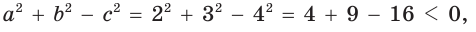
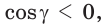
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
Следствие:
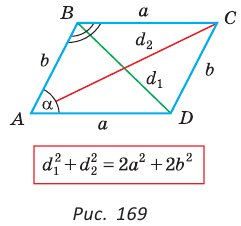
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Доказательство:
Пусть в параллелограмме ABCD 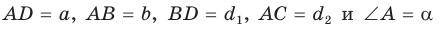
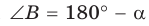
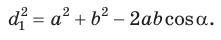
Из 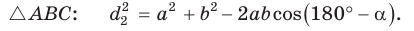
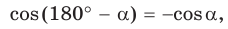
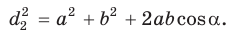
Сложив почленно равенство (1) и равенство (2), получим 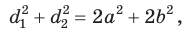
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
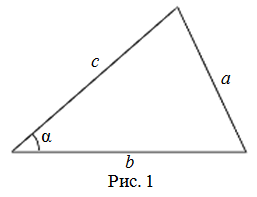
Следствие:
Медиану 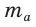
Доказательство:
Рассмотрим 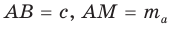
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма 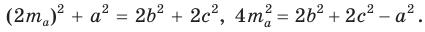
Утверждение доказано.
Аналогично:
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, 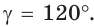
Решение:
а) По теореме косинусов
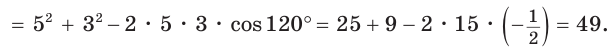
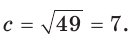
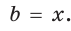
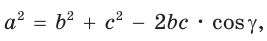
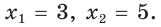
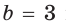
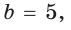
Ответ: а) 7; б) 3 или 5.
Пример:
Две стороны треугольника равны 6 и 10, его площадь —
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Решение:
Пусть в 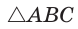
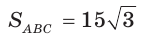
Поскольку 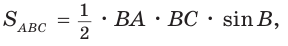
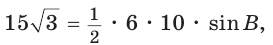
Так как 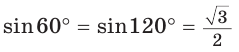
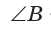

Ответ: 14.
Пример:
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника 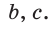
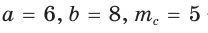
По формуле медианы 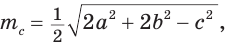
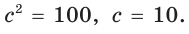
Ответ: 24.
Формула Герона
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: 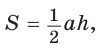
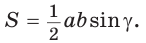
Теорема (формула Герона).
Площадь треугольника со сторонами 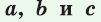
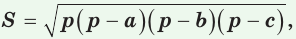
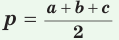
Доказательство:
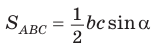
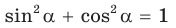
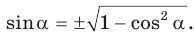
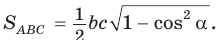
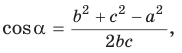
Тогда
Так как
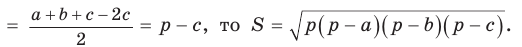
Решение треугольников
Решением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
Пример №1 (решение треугольника по двум сторонам и углу между ними).
Дано: 
Найти :
Решение:
Рис. 184
1) По теореме косинусов
2) По следствию из теоремы косинусов
3) Угол 
4) Угол
Замечание. Нахождение угла 
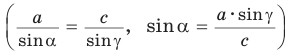
Пример №2 (решение треугольника по стороне и двум прилежащим к ней углам).
Дано: 
Найти:
Решение:
1) Угол
2) По теореме синусов 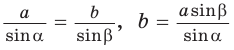
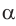
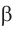
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: 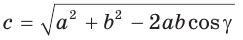
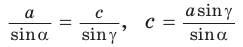
Пример №3 (решение треугольника по трем сторонам).
Дано: 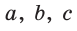
Найти: 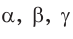
Решение:
1) По следствию из теоремы косинусов
2) Зная 
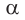
3) Аналогично находим угол
4) Угол
5) Радиус R описанной окружности треугольника можно найти по формуле 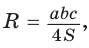
Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов 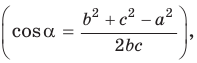
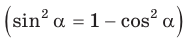
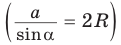
Пример №4
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим:
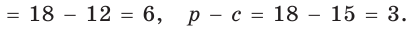
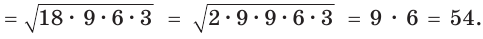
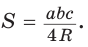
Ответ:
Способ 2. Так как 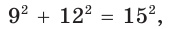
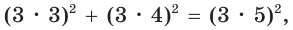
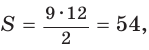
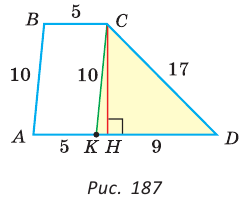
Пример №5
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и 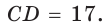
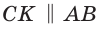
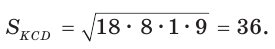
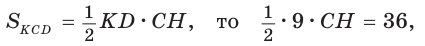
Ответ: 76.
Примеры решения задач с использованием теоремы синусов и теоремы косинусов
Пример:
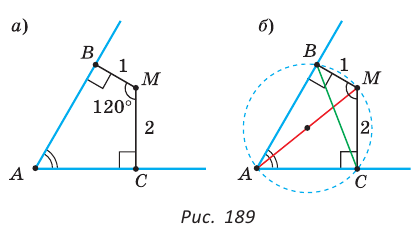
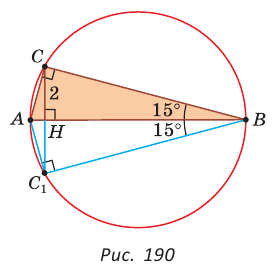
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть 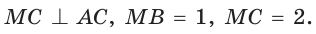
длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°.
Поэтому
Так как в четырехугольнике АВМС 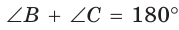
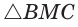
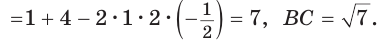
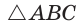
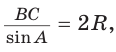
Ответ:
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
Пример №6
В прямоугольном треугольнике АВС известно: 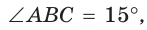
Решение:
Построим 
Поскольку 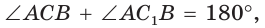
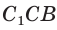
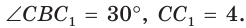
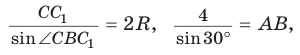
Ответ: 8.
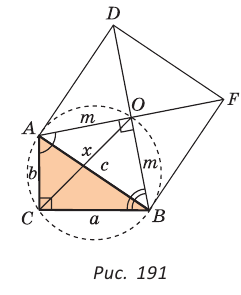
Пример №7
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = 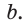
Решение:
Способ 1. Так как 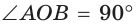
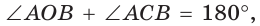
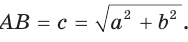
Пусть СО = х. По теореме косинусов из 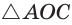
из 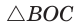
По свойству вписанного четырехугольника 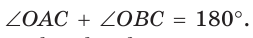
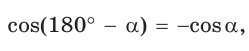
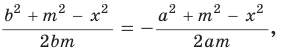
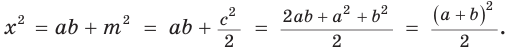
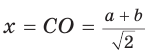
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
Способ 3. Достроим 
Ответ:
Пример №8
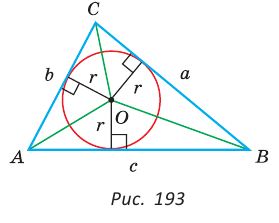
Точка О — центр окружности, вписанной в треугольник АВС, 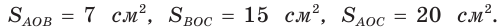
Решение:
Пусть 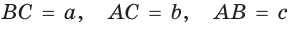
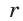
Тогда
Отсюда 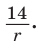
С другой стороны, 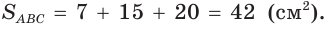
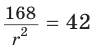
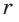
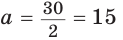
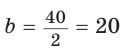
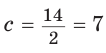
Ответ: 15 см; 20 см; 7 см.
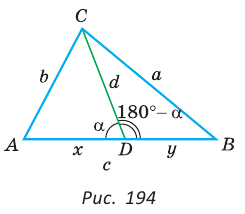
Теорема Стюарта
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
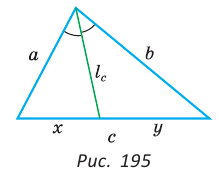
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
Доказательство:
По теореме косинусов из 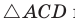
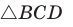
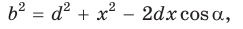
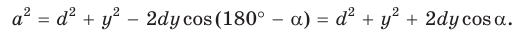
Умножим обе части равенства (1) на у, равенства (2) — на
Сложим почленно полученные равенства:
Из последнего равенства выразим
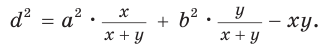
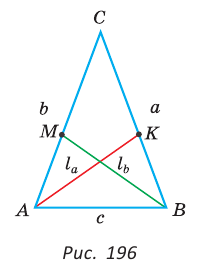
Следствие:
Биссектрису треугольника можно найти по формуле (рис. 195)
Доказательство:
По свойству биссектрисы треугольника 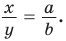
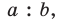
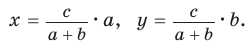
Пример №9
Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
Пусть дан треугольник АВС, 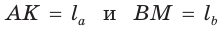
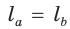
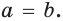
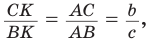
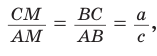
По формуле биссектрисы треугольника
Из условия 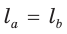
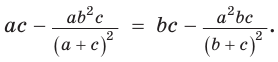
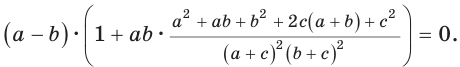
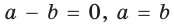
Теорема Птолемея о вписанном четырехугольнике
Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон, т. е.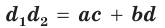
Доказательство:
Из 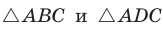
Так как 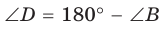
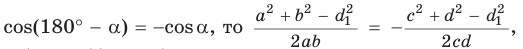
Аналогично из 
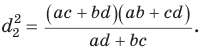
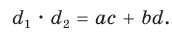
Запомните:
- Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу его описанной окружности:
- Радиус описанной окружности треугольника можно найти, используя формулы:
- Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
- Пусть
— стороны треугольника и с — большая сторона. Если
, то треугольник тупоугольный, если
то треугольник остроугольный, если
, то треугольник прямоугольный.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
- Формула Герона:
- Формула медианы:
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм





















































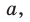
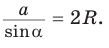
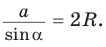
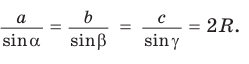
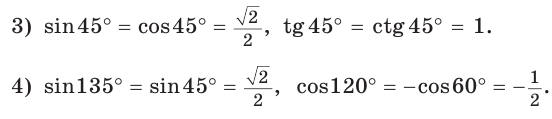
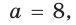
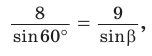
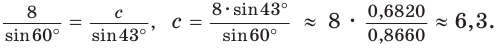
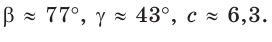


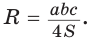
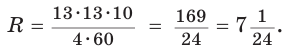
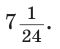
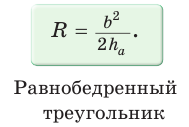
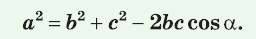
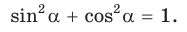
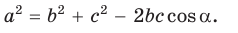
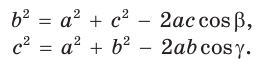
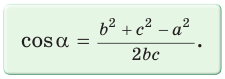
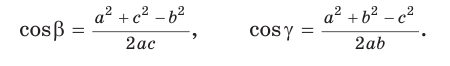

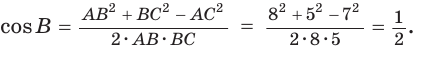
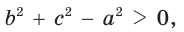 то
то 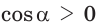 и угол
и угол 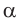 острый;
острый;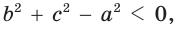 то
то 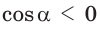 и угол
и угол 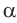 тупой;
тупой; то
то 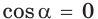 и угол
и угол 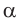 прямой.
прямой.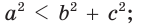
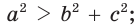
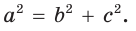
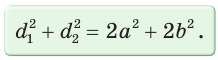
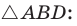
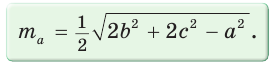
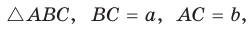
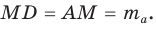
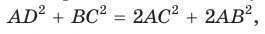
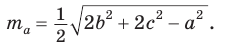
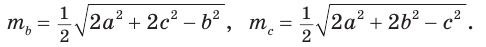
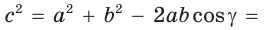
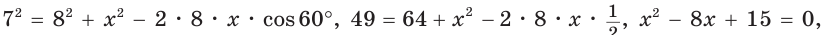
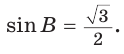
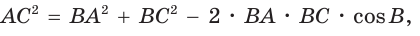
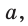
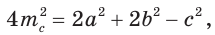
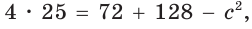
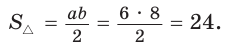
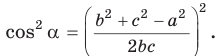
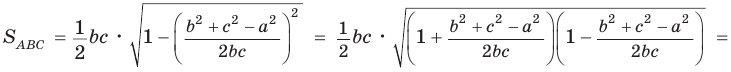
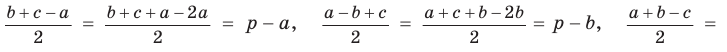
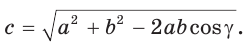
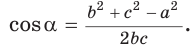
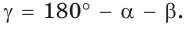
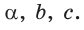
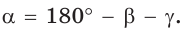
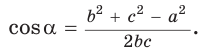
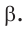
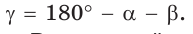
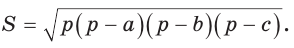
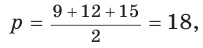
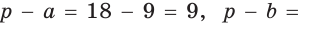
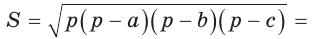
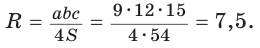
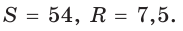
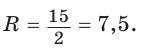
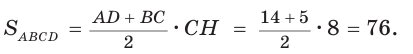
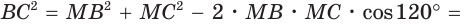
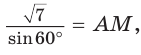
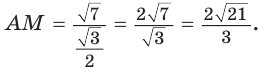
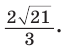
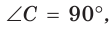
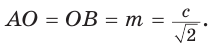
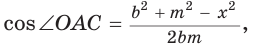
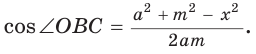
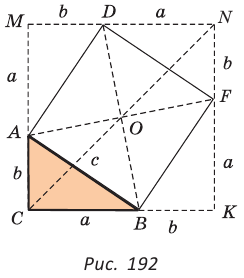
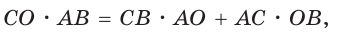
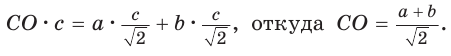
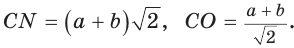
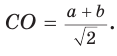
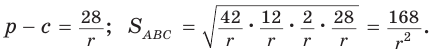
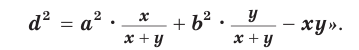
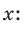
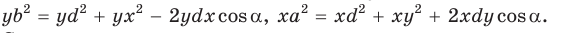
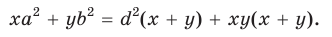
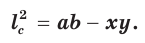
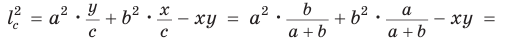
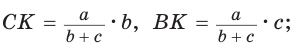
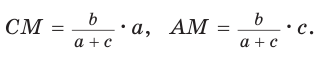
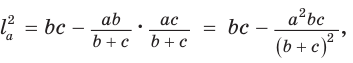
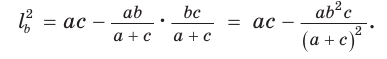
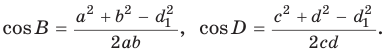
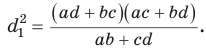
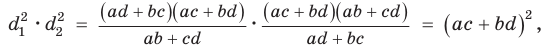
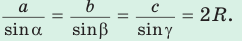
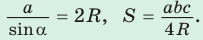
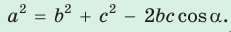
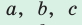 — стороны треугольника и с — большая сторона. Если
— стороны треугольника и с — большая сторона. Если 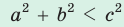 , то треугольник тупоугольный, если
, то треугольник тупоугольный, если 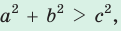 то треугольник остроугольный, если
то треугольник остроугольный, если 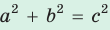 , то треугольник прямоугольный.
, то треугольник прямоугольный.