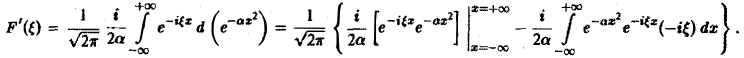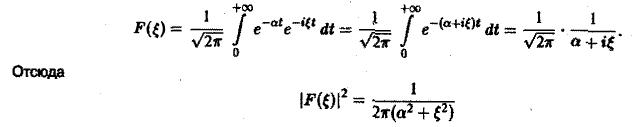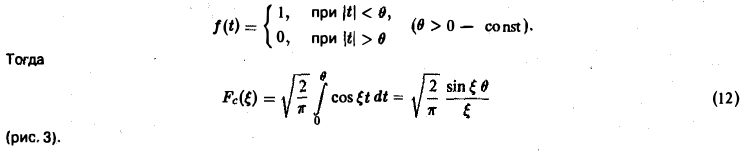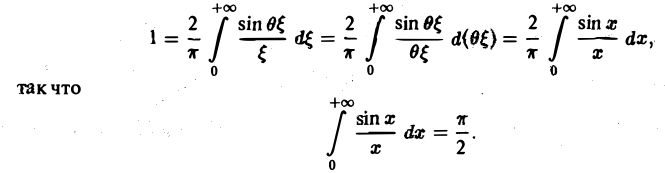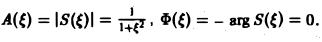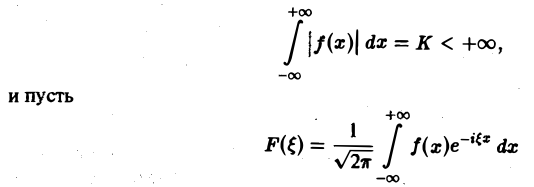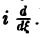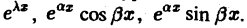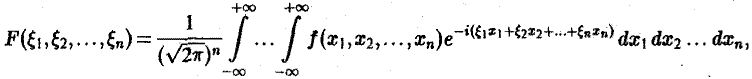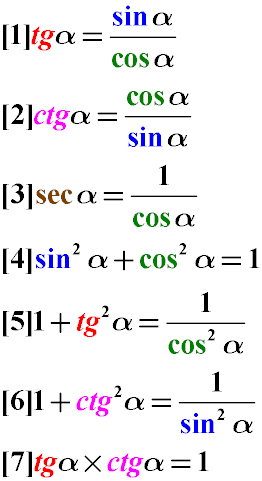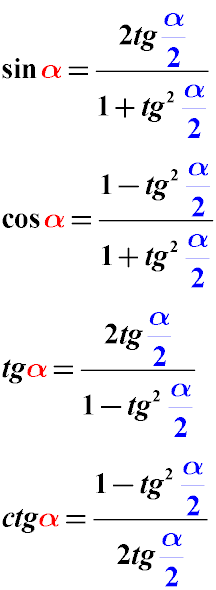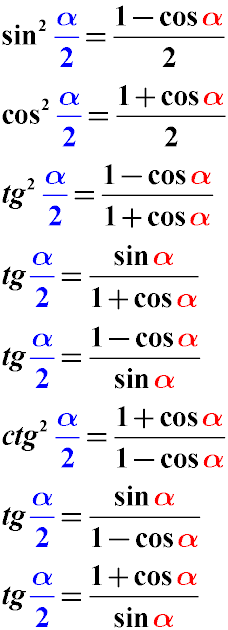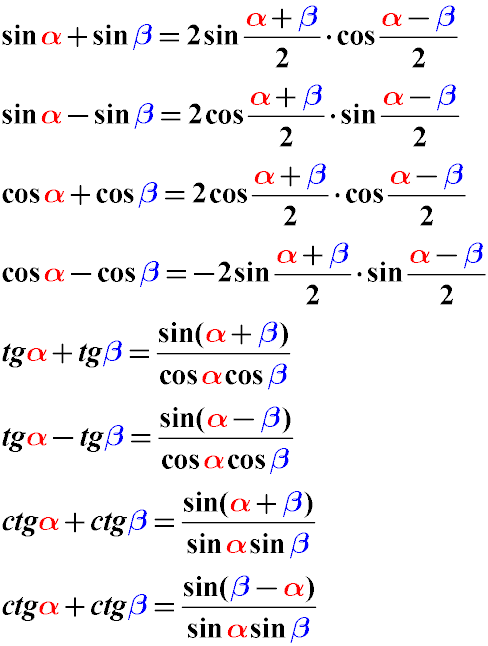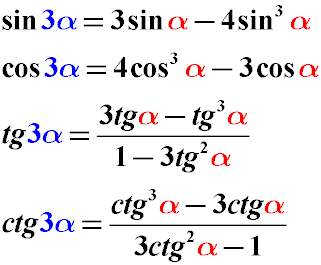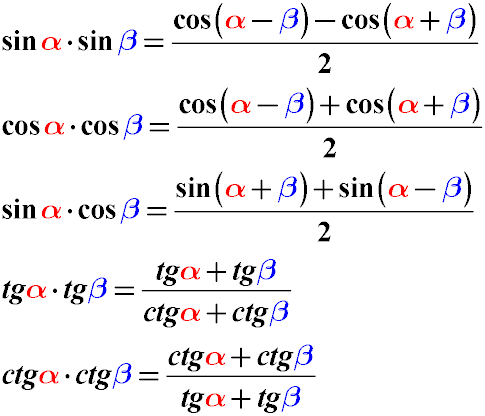Как найти косинус преобразования - Сайт, где вы сможете решить свои вопросы

Интеграл Фурье
Комплексная форма интеграла Фурье
Преобразование Фурье. Косинус- и синус-преобразования Фурье
Косинус- и синус-преобразования Фурье
Амплитудный и фазовый спектры интеграла Фурье
Свойства преобразования Фурье
Приложения преобразования Фурье
Понятие о многомерном преобразовании Фурье
Дополнение к преобразованию Фурье

Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.

Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(х) называется функция (*)

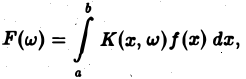
где К(х, w) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).

Интеграл Фурье

Всякая функция f(x), которая на отрезке [— l, l] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом (1)

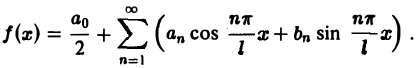
Коэффициенты аn и bn ряда (1) определяются по формулам Эйлера—Фурье:
(2)

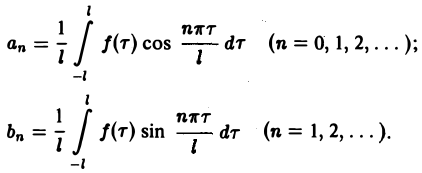
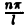
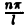
Ряд в правой части равенства (1) можно записать в иной форме. С этой целью внесем в него из формул (2) значения коэффициентов аn и bn, подведем под знаки интегралов cos х и sin х (что возможно, поскольку переменной интегрирования является τ) и используем формулу для косинуса разности. Будем иметь
(3)

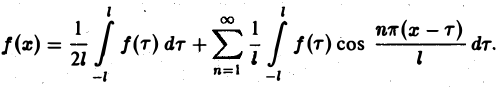
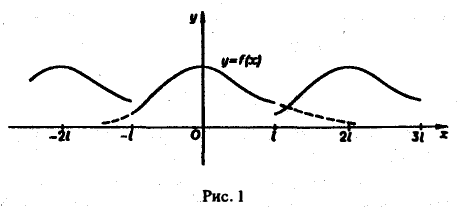
Если функция f(x) первоначально была определена на интервале числовой оси, большем, чем отрезок [-l, l] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-l, l] и продолжит ее на всю числовую ось как периодическую функцию с периодом 2l (рис. 1).

Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при l → +∞. При этом естественно потребовать выполнения следующих условий:

1, f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;

2. функция f(x) абсолютно интегрируема на всей числовой оси,

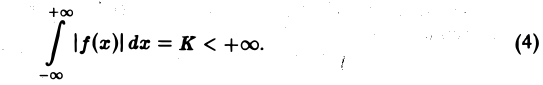
При выполнении условия 2 первое слагаемое правой части равенства (3) при l → +∞ стремится к нулю. В самом деле,

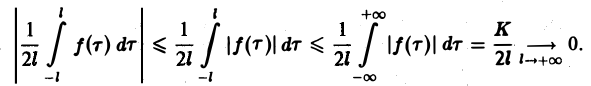
Попытаемся установить, во что перейдет в пределе при l → +∞ сумма в правой части (3). Положим

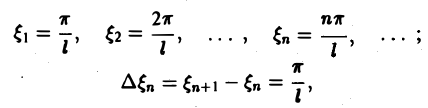
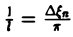
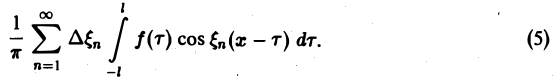
так, что . Тогда сумма в правой части (3) примет вид

В силу абсолютной сходимости интеграла эта сумма при больших l мало отличается от выражения

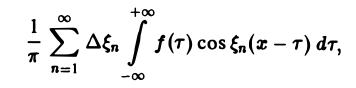
которое напоминает интегральную сумму для функции переменного ξ

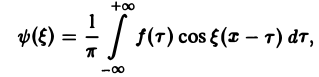
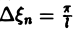
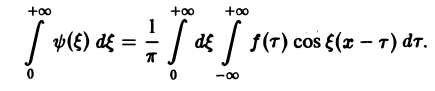
составленную для интервала (0, + ∞) изменения Поэтому естественно ожидать, что при l → +∞ ( → 0) сумма (5) перейдет в интеграл

С другой стороны, при l → +∞ (х фиксировано) из формулы (3) вытекает, что

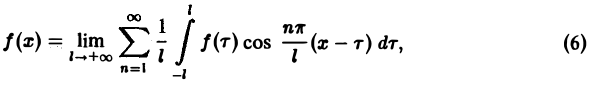
и мы получаем равенство
(7)

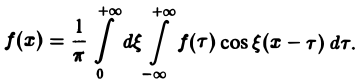
Достаточное условие справедливости формулы (7) выражается следующей теоремой.

Теорема:

Если функция f(x) абсолютно интегрируема на всей числовой оси — ∞ < х < + ∞ и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке [а, b], то справедливо равенство

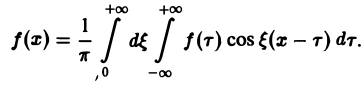
При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции f(x), значение интеграла в правой части (7) равно

j [/(^о — 0) + f(xo + 0)].

Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралам Фурье.

Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде (8)

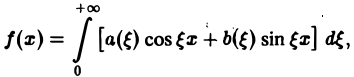
где

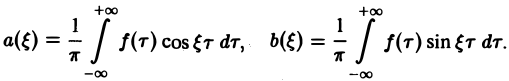
Функции а( ξ ), b( ξ ) являются аналогами соответствующих коэффициентов Фурье an и bn 2π-периодической функции, но последние определены для дискретных значений п, в то время как а( ξ ), b( ξ ) определены для непрерывных значений ξ ∈ (— ∞, + ∞).

Комплексная форма интеграла Фурье

Предполагая f(x) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл

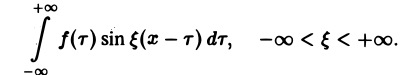
Этот интеграл равномерно сходится для — ∞ < ξ < + ∞, так как

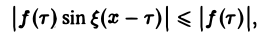
и потому представляет собой непрерывную и, очевидно, нечетную функцию от ξ. Но тогда

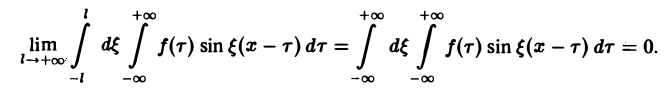
С другой стороны, интеграл

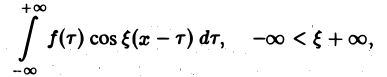
есть четная функция переменной так что

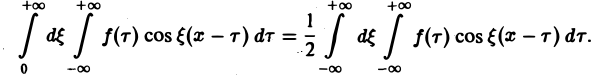
Поэтому интегральную формулу Фурье можно записать так:

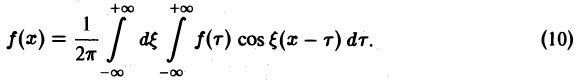
Умножим равенство

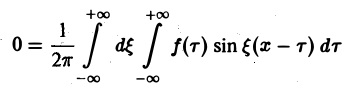
на мнимую единицу i и прибавим к равенству (10). Получим

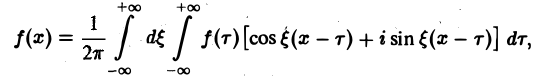
откуда, в силу формулы Эйлера (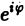= cos φ + i sin φ), будем иметь
(11)

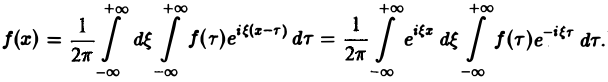
Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по ξ понимается в смысле главного значения по Коши:

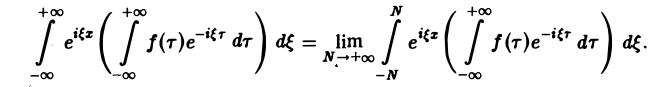
Преобразование Фурье. Косинус- и синус-преобразования Фурье

Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.

Определение:

Функция

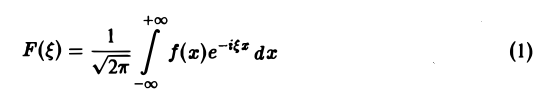
называется преобразованием Фурье функции f(x) (спектральной функцией).

Это — интегральное преобразование функции f(x) на интервале (- ∞ ,+ ∞) с ядром

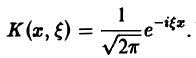
Используя интегральную формулу Фурье

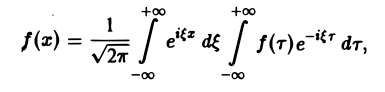
получаем
(2)

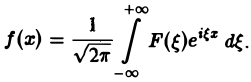
Это так называемое обратное преобразование Фурье, дающее переход от F( ξ ) к f(x). Иногда прямое преобразование Фурье задают так:

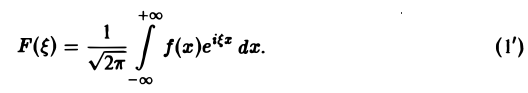
Тогда обратное преобразование Фурье определится формулой

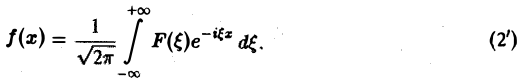
Преобразование Фурье F( ξ ) функции f(х) определяют также следующим образом:

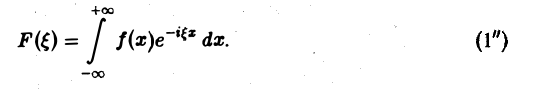
Тогда, в свою очередь,

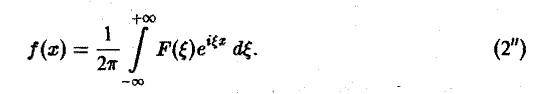
При этом положение множителя 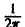достаточно произвольно: он может входить либо в формулу (1″), либо в формулу (2″).

Пример:

Найти преобразование Фурье функции

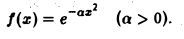
Имеем

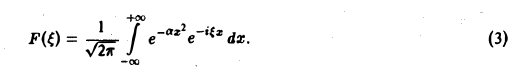
Это равенство допускает дифференцирование по ξ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда ξ принадлежит любому конечному отрезку):

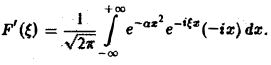
Интегрируя по частям, будем иметь

Внеинтегральное слагаемое обращается в нуль, и мы получаем

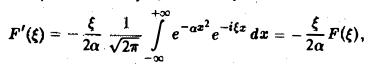
откуда

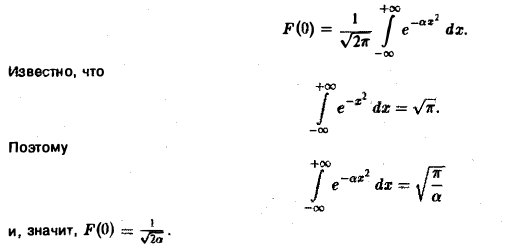
(С — постоянная интегрирования). Полагая в (4) ξ = 0, найдем С —F(0). В силу (3) имеем

Таким образом,

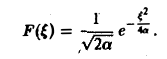
В частности, для

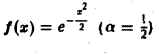
получаем, что

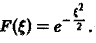
Пример:

Разряд конденсатора через сопротивление. Рассмотрим функцию

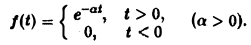
Для спектральной функции F( ξ ) получаем

(рис. 2).

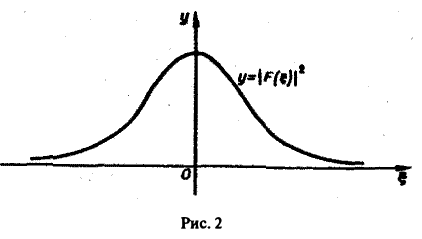
Условие абсолютной интегрируемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как f(x) = 1. f(x) = x³, f(х) = cosx, f(х) = е^х, для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.

Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| → + ∞ (как в примерах 1 и 2).

Косинус- и синус-преобразования Фурье

Используя формулу косинуса, разности, перепишем интегральную формулу Фурье

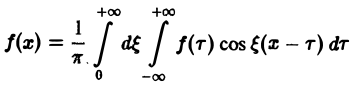
в следующем виде:

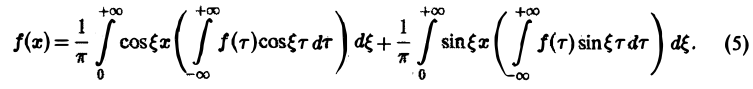
Пусть f(x) — четная функция. Тогда

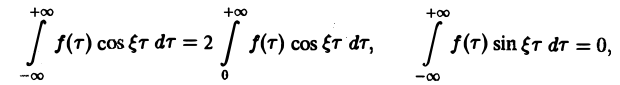
так что из равенства (5) имеем
(6)

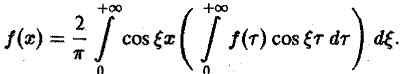
В случае нечетной f(x) аналогично получаем
(7)

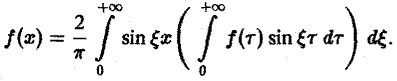
Если f(х) задана лишь на (0, + ∞), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным.

Определение:

Функция

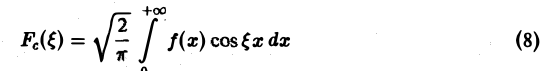
называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x)

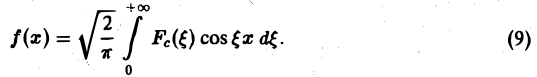
Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc( ξ ). Иными словами, функции f и Fc являются взаимными косинус-преобразованиями.

Определение:

Функция

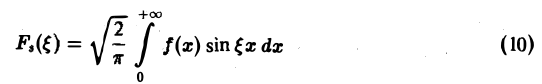
называется синус-преобразованием Фурье функции f(x).
Из (7) получаем, что для нечетной функции f(х)

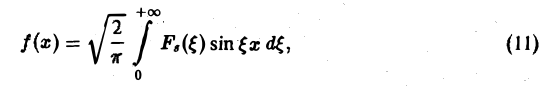
т.е. f и Fs являются взаимными синус-преобразованиями.

Пример:

Прямоугольный импульс. Пусть f(t) — четнaя функция, определенная следующим образом:

Воспользуемся полученным результатом для вычисления интеграла

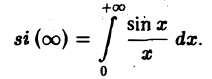
В силу формулы (9) имеем

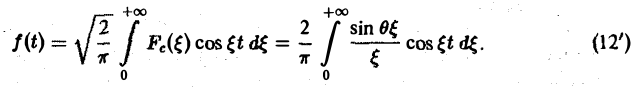
В точке t = 0 функция f(t) непрерывна и равна единице.

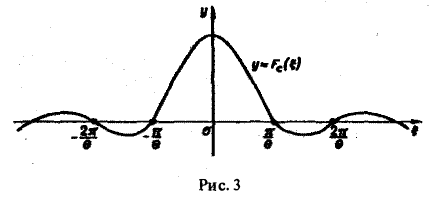
Поэтому из (12′) получим

Амплитудный и фазовый спектры интеграла Фурье

Пусть периодическая с периодом 2π функция f(х) разлагается в ряд Фурье

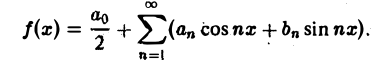
Это равенство можно записать в виде

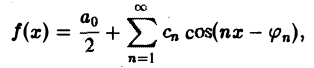
где Cn = 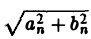— амплитуда колебания с частотой п, φn — фаза. На этом пути мы приходим к понятиям амплитудного и фазового спектров периодической функции.

Для непериодической функции f(x), заданной на (- ∞, + ∞), при определенных условиях оказывается возможным представить ее интегралом Фурье

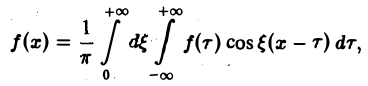
осуществляющим разложение этой функции по всем частотам 0 < ξ < + ∞ (разложение по непрерывному спектру частот).

Определение:

Спектральной функцией, или спектральной плотностью интеграла Фурье, называется выражение

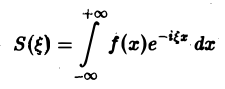
(прямое преобразование Фурье функции f(х)).

Функция

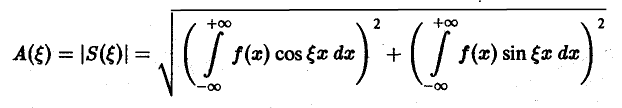
называется амплитудным спектром, а функция

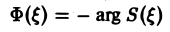
(0 — фазовым спектром функции f(x).

Амплитудный спектр A (ξ) служит мерой вклада частоты ξ в функцию f(х).

Пример:

Найти амплитудный и фазовый спектры функции

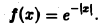
Находим спектральную функцию

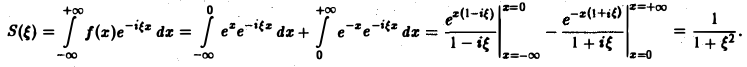
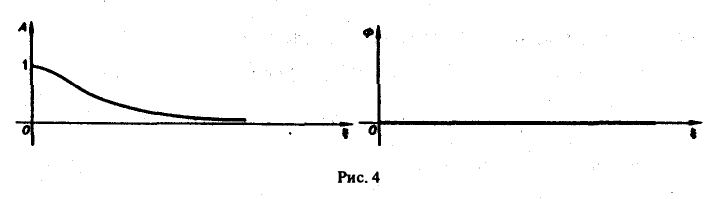
Отсюда

Графики этих функций изображены на рис. 4.

Свойства преобразования Фурье

1, Линейность. Если F( ξ ) и G( ξ ) — преобразования Фурье функций f(х) и g(х) соответственно, то при любых постоянных а и β преобразованием Фурье функции а f(х) + β g(х) будет функция a F( ξ ) + βG( ξ ).

Пользуясь свойством линейности интеграла, имеем

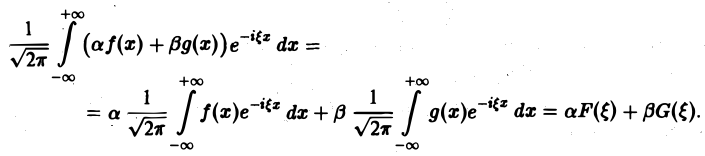
Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через будем писать

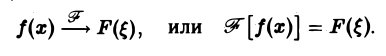
Если F( ξ ) есть преобразование Фурье абсолютно интегрируемой на всей числовой оси функции f(х), то F( ξ ) ограничена при всех ξ ∈ (— ∞, + ∞).

Пусть функция f(х) абсолютно интегрируема на всей оси — ∞ < х < + ∞,

— преобразование Фурье функции f(х). Тогда

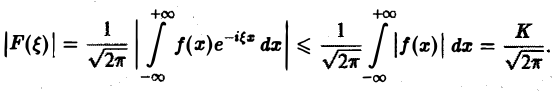
Задача:

Пусть f(x) — функция, допускающая преобразование Фурье, h — действительное число. Функция fh(x) = f(x-h) называется сдвигом функции f(x). Пользуясь определением преобразования Фурье, показать, что

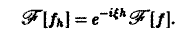
Задача:

Пусть функция f(x) имеет преобразование Фурье F( ξ ), h — действительное число. Показать, что

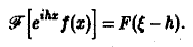
3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция f(х) имеет производную f'(х), также абсолютно интегрируемую на всей оси Ох, так что f(х) стремится к нулю при |х| —► + ∞. Считая f'(х) гладкой функцией, запишем

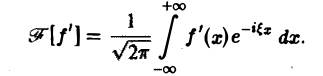
Интегрируя по частям, будем иметь

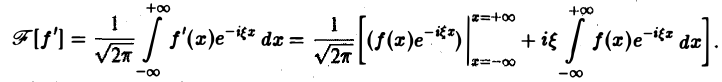
Внеинтегральное слагаемое обращается в нуль (так как f(х) → 0 при |х| → + ∞), и мы получаем (1)

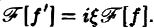
Таким образом, дифференцированию функции f(х) отвечает умножение ее образа Фурье [f] на множитель iξ.

Если функция f(х) имеет гладкие абсолютно интегрируемые производные до порядка m включительно и все они, как и сама функция f(х), стремятся к нулю при |x| → + ∞, то, интегрируя по частям нужное число раз, получим

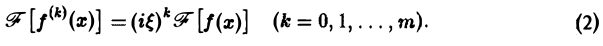
Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину iξ и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.

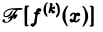
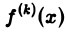
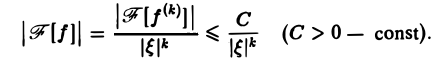
Так как преобразование Фурье абсолютно интегрируемой функции есть ограниченная функция от ξ (свойство 2), то из соотношения (2) получаем для [f] следующую оценку:

Из этой оценки следует: чем больше функция f(х) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при | ξ | → + ∞.

Замечание:

Условие 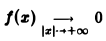является достаточно естественным, поскольку обычная теория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и конец, но не продолжаются неограниченно с примерно одинаковой интенсивностью.

4. Связь между скоростью убывания функции f(x) при |х| → + ∞ и гладкостью ее преобразования Фурье. Предположим, что не только f(x), но и ее произведение хf(х) является абсолютно интегрируемой функцией на всей оси Ох. Тогда преобразование Фурье

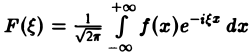
функции f(x) будет дифференцируемой функцией.

Действительно, формальное дифференцирование по параметру ξ подынтегральной функции приводит к интегралу

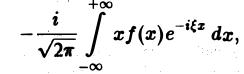
который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и

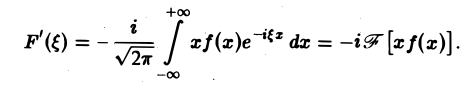
Таким образом,

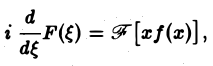
т. е. операция умножения f(х) на аргумент х переходит после преобразования Фурье в операцию

Если вместе с функцией f(х) абсолютно интегрируемыми на всей оси Ох являются функции хf(х)…..х^mf(х), то процесс дифференцирования можно продолжить.

Получим, что функция F( ξ ) = [f(х)] имеет производные до порядка m включительно, причем

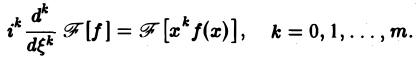
Таким образом, чем быстрее функция f(х) убывает при |х| → + ∞, тем более гладкой получается функция F( ξ ) = [f(х)].

Теорема:

О свертке. Пусть F1( ξ ) и F2( ξ ) — преобразования Фурье функций f1(x) и f2(x) соответственно. Тогда

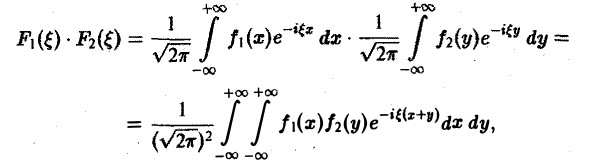
причем двойной интеграл в правой части сходится абсолютно.

Положим х + у = т, так что у = т — х. Тогда будем иметь

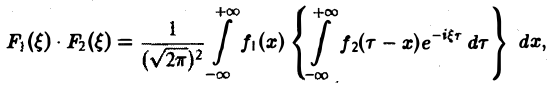
или, меняя порядок интегрирования,

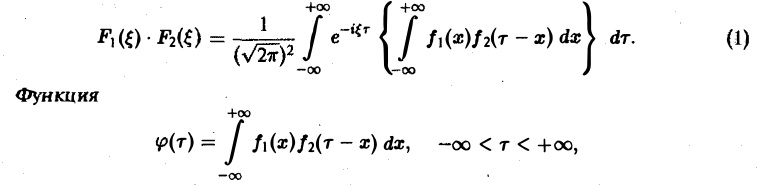
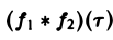
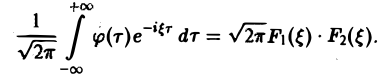
называется сверткой функций f(x) и f2(x) и обозначается символом . Формула (1) может быть теперь записана так:

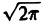
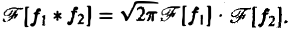
Отсюда видно, что преобразование Фурье свертки функций f1(x) и f2(x) равно умноженному на произведению преобразований Фурье свертываемых функций,

Замечание:

Нетрудно установить следующие свойства свертки:

1) линейность:

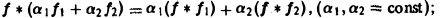
2) коммутативность:

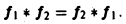
Приложения преобразования Фурье

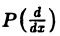
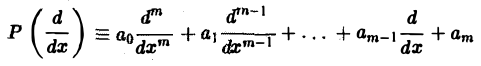
1, Пусть — линейный дифференциальный оператор порядка m с постоянными коэффициентами,

(аo, a1,… ,ат = const). Используя формулу для преобразования Фурье производных функции у(х), находим

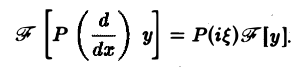
Рассмотрим дифференциальное уравнение

где 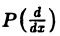— введенный выше дифференциальный оператор.

Предположим, что искомое решение у(х) имеет преобразование Фурье y(ξ), а функция f(x) имеет преобразование f( ξ ). Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси Oξ относительно y(ξ)

так что формально

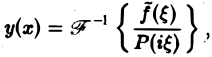
где символ 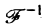обозначает обратное преобразование Фурье.

Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида

Они не являются абсолютно интегрируемыми на оси — ∞ < х < + ∞, и преобразование Фурье для них не определено, так что, строго говоря, применять данный метод нельзя. Это ограничение можно обойти, если ввести в рассмотрение так называемые обобщенные функции. Однако в ряде случаев преобразование Фурье все же применимо в своей классической форме.

Пример:

Найти решение u = u(x,t) уравнения

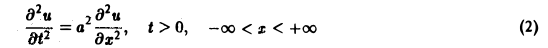
(а = const), при начальных условиях

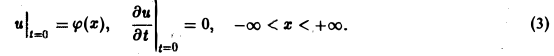
Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение φ(х) точек струны, а начальные скорости отсутствуют.

Поскольку пространственная переменная х изменяется в пределах от — ∞ до + ∞, подвергнем уравнение и начальные условия преобразованию Фурье по переменной х. Будем предполагать, что

1) функции u(z, t) и φ(x) — достаточно гладкие и стремятся к нулю при х → + ∞ и ∀t ≥ О настолько быстро, что существуют преобразования Фурье

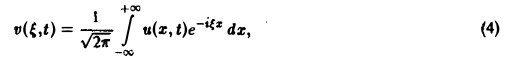
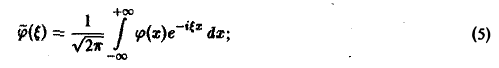
2) допустимы операции дифференцирования, так что

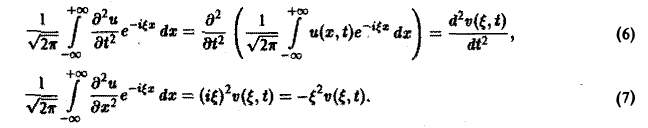
Умножая обе части (2) на 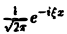и интегрируя по x от — ∞ до + ∞, получим

а из начальных условий (3) найдем

Таким образом, применяя к задаче (2)-(3) преобразование Фурье, приходим к задаче Коши (8)—(10) для обыкновенного дифференциального уравнения, где ξ — параметр. Решением уравнения (8) является функция

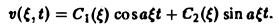
Из условий (9) и (10) находим, что С1( ξ ) = φ( ξ ). C2( ξ ) = 0, так что v( ξ, t) = φ( ξ )cos aξt. Применяя обратное преобразование Фурье, получим

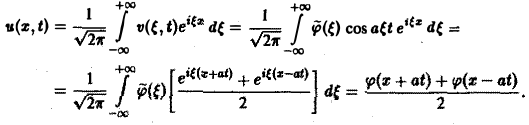
Это частный случай формулы Даламбера решения задачи (2)-(3).

2. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т. е. уравнений, в которых неизвестная функция входит под знак интеграла.

Рассмотрим, например, уравнение

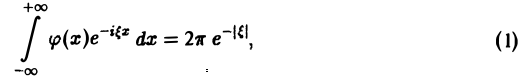
где φ(х) — искомая функция. Записав (1) в виде

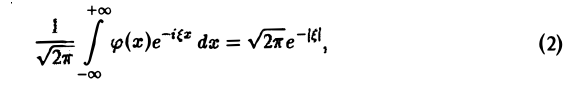
замечаем, что левую часть (2) можно рассматривать как преобразование Фурье функции φ(х), так что (2) равносильно следующему равенству:

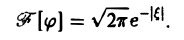
Тогда по формуле обращения

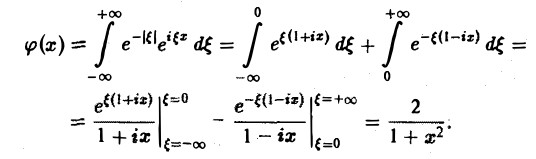
Функция 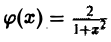есть решение уравнения (1).

Понятие о многомерном преобразовании Фурье

Преобразование Фурье:

Пусть

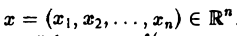
Многомерным преобразованием Фурье абсолютно интегрируемой функции f(х1, х2,…, хb) называется функция

или, короче,

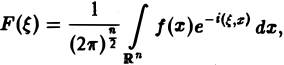
где

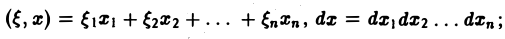
символ 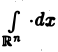обозначает интегрирование по всему пространству Rⁿ.

Свойства многомерного преобразования аналогичны соответствующим свойствам преобразования Фурье функции одной переменной. В специальном случае, когда

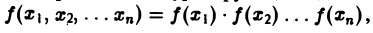
имеем

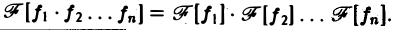
Дополнение к преобразованию Фурье

Смотрите также:

Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник

Синус-преобразование Фурье и косинус-преобразование Фурье — одни из видов преобразований Фурье, не использующих комплексные числа.

Определение[править | править код]

Синус-преобразование Фурье[править | править код]

Синус-преобразование Фурье ${displaystyle {hat {f}}^{s}}$ или ${displaystyle {mathcal {F}}_{s}(f)}$ функции f(t) равно

${displaystyle 2int limits _{-infty }^{infty }f(t)sin ,{2pi nu t},dt.}$

где

— время,

— частота колебаний.

Функция ${displaystyle {hat {f}}^{s}(nu )}$ нечётна по , то есть

${displaystyle {hat {f}}^{s}(nu )=-{hat {f}}^{s}(-nu )}$

для любого

Косинус-преобразование Фурье[править | править код]

Косинус-преобразование Фурье ${displaystyle {hat {f}}^{c}}$ или ${displaystyle {mathcal {F}}_{c}(f)}$ функции f(t) равно

${displaystyle 2int limits _{-infty }^{infty }f(t)cos ,{2pi nu t},dt.}$

где

— время,

— частота колебаний.

Функция ${displaystyle {hat {f}}^{c}(nu )}$ чётна по , то есть
${displaystyle {hat {f}}^{c}(nu )={hat {f}}^{c}(-nu )}$ для любого .

Обратное синус- и косинус-преобразование Фурье[править | править код]

Изначальная функция f(t) может быть найдена по формуле

${displaystyle f(t)=int _{0}^{infty }{hat {f}}^{c}cos(2pi nu t)dnu +int _{0}^{infty }{hat {f}}^{s}sin(2pi nu t)dnu .}$

Используя формулу сложения для косинуса, получим, что

${displaystyle {frac {pi }{2}}(f(x+0)+f(x-0))=int _{0}^{infty }int _{-infty }^{infty }cos omega (t-x)f(t)dtdomega ,}$

где

— право- и левосторонние пределы соответственно.

Если функция f(t) чётная, то часть формулы с синусом обращается в нуль, если f(t) нечётная, то исчезает косинус.

Расширение на комплексные числа[править | править код]

Сегодня чаще используется формула синус- и косинус-преобразования Фурье в комплексном виде

${displaystyle {hat {f}}(nu )=int limits _{-infty }^{infty }f(t)e^{-2pi inu t},dt.}$

Используя формулу Эйлера, получим

${displaystyle {hat {f}}(nu )=int limits _{-infty }^{infty }f(t)(cos ,{2pi nu t}-i,sin {2pi nu t}),dt=int limits _{-infty }^{infty }f(t)cos ,{2pi nu t},dt-iint limits _{-infty }^{infty }f(t)sin ,{2pi nu t},dt={frac {1}{2}}{hat {f}}^{c}(nu )-{frac {i}{2}}{hat {f}}^{s}(nu ).}$

См. также[править | править код]

Преобразование Фурье;
Дискретное косинусное преобразование.

Ссылки[править | править код]

Whittaker, Edmund, and James Watson, A Course in Modern Analysis, Fourth Edition, Cambridge Univ. Press, 1927, стр. 189, 211

Источник

Пусть — четная функция. Вспомним формулу (11.12):

перепишем ее в виде

и положим

Тогда (11.20) даст нам

Формула (11.21) определяет косинус-преобразование Фурье четной функции приводящее к функции также называемой косинус-преобразованием функции Формула (11.22) определяет обратное косинус-преобразование.

Источник

Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:

Простейшие тригонометрические тождества

Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств.
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).

Преобразование отрицательных углов тригонометрических функций (четность и нечетность)

Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.

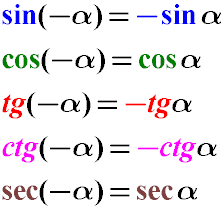
Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс – нечетные функции.

Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус “минус альфа” даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.

Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)

Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:

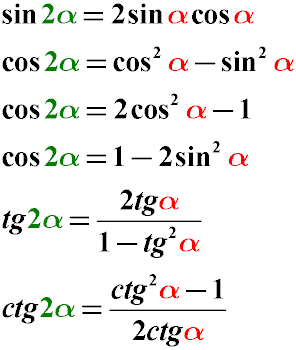
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:

Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла

Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла

Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица

Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла

Тангенс двойного угла равен дроби, числитель которой – удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.

Котангенс двойного угла равен дроби, числитель которой – квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла

Формулы универсальной тригонометрической подстановки

Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .

Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.

Тригонометрические тождества преобразования половины угла

Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.

Тригонометрические формулы сложения углов

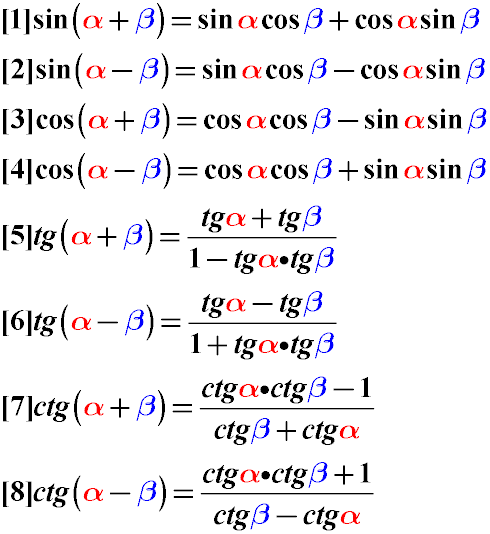
cos (α – β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α

sin (α – β) = sin α · cos β – sin β · cos α
cos (α + β) = cos α · cos β – sin α · sin β

Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:

Тангенс суммы углов равен дроби, числитель которой – сумма тангенса первого и тангенса второго угла, а знаменатель – единица минус произведение тангенса первого угла на тангенс второго угла.

Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель – единице плюс произведение тангенсов этих углов.

Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.

Котангенс разности углов равен дроби, числитель которой – произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.

Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.

Формулы преобразования суммы или разности тригонометрических функций

Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:

Формулы тройного угла – преобразование sin3α cos3α tg3α в sinα cosα tgα

Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:

Формулы преобразования произведения тригонометрических функций

Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:

В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.

Формулы приведения тригонометрических функций

Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце – угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .

См. также Полный список формул приведения тригонометрических функций.

Угол	α + 90 α + π/2	α + 180 α + π	α + 270 α + 3π/2	90 – α π/2- α	180 – α π- α	270 – α 3π/2- α	360 – α 2π- α
sin	cos α	-sin α	-cos α	cos α	sin α	-cos α	-sin α
cos	-sin α	-cos α	sin α	sin α	-cos α	-sin α	cos α
tg	-ctg α	tg α	-ctg α	ctg α	-tg α	ctg α	-tg α
ctg	-tg α	ctg α	-tg α	tg α	-ctg α	tg α	-ctg α

Начать курс обучения

Источник

План урока:

Основное тригонометрическое тождество

Тригонометрические функции суммы и разности

Формулы двойного угла

Формулы понижения степени

Формулы приведения

Сумма тригонометрических функций

Произведение тригонометрических функций

Основное тригонометрическое тождество

Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:

1dfgdfg

Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:

АВ² + ОВ² = ОА²

Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:

sin²α + соs²α = 1

Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.

2gfdg

Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?

Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:

sin²α + соs²α = 1

0,8² + соs²α = 1

0,64 + соs²α = 1

соs²α = 1 – 0,64

соs²α = 0,36

соsα = – 0,6 или соsα = 0,6

Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.

Ответ: 0,6.

Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:

3hghfgh

По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.

Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.

Решение.

sin²α + соs²α = 1

0,28² + sin²α = 1

0,0784 + sin²α = 1

sin²α = 1 – 0,0784

sin²α = 0,9216

sin α = –0,96 или sin α = 0,96

Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.

Ответ: – 0,96.

Задание. Найдите tgα, если sinα = 5/13 и π/2 < α < π.

Решение. Здесь задача уже в два действия! Сначала определим соsα:

sin²α + соs²α = 1

соs²α = 1 – sin²α = 1 – (5/13)² = 169/169 – 25/169 = 144/169

соsα = – 12/13 или соsα = 12/13

Условие π/2 < α < π указывает на то, что угол относится ко II четверти, в которой косинус отрицателен, поэтому соsα = – 12/13.

Далее находим тангенс, просто деля синус на косинус:

tgα = sinα:соsα = (5/13):(12/13) = (5/13)•(13/12) = 5/12

Ответ: 5/12

Рассмотренный пример показал нам, что, зная синус, можно рассчитать не только косинус, но и тангенс. А возможно ли совершить обратное действие, найти по тангенсу синус или косинус? Да, но для этого нужно получить новую тригонометрическую формулу.

Запишем тождество

sin²α + соs²α = 1

Далее поделим его на величину соs²α:

4gfdfg

Крайнее левое слагаемое – это величина tg²α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:

5hgjg

В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin²α:

6gfgh
7hgfgh

Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.

Решение.

Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:

8hgh

Так как угол относится к III четверти, где косинус отрицателен, то

соsα = – 0,8

Синус угла найдем, используя основное тригон-кое тождество:

sin²α + соs²α = 1

sin²α = 1 – соs²α = 1 – (– 0,8)² = 1 – 0,64 = 0,36

sinα = – 0,6 или sinα = 0,6

С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6

Ответ: sinα = – 0,6; соsα = – 0,8.

Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin²α + соs²α = 1 несложно получить из выражения

sin²α = 1 – соs²α

соs²α = 1 – sin²α

которые помогают в работе с длинными ф-лами.

Задание. Упростите выражение

4sin²α + 9соs²α – 6

таким образом, чтобы в нем не содержалось синуса.

Решение. Произведем замену sin²α = 1 – соs²α:

4sin²α+ 9соs²α – 6 = 4(1 – соs²α)+ 9соs²α – 6 =

= 4 – 4 соs²α + 9соs²α – 6 = 5соs²α – 2

Видим, что получилось значительно более простое выражение.

Ответ: 5соs²α – 2.

Задание. Избавьтесь от синуса в выражении

sin⁴α – соs⁴α

Решение. Воспользуемся ф-лой разности квадратов:

sin⁴α – соs⁴α = (sin²α – соs²α)(sin²α + соs²α) = (sin²α – соs²α)•1 =

= 1 – соs²α– соs²α = 1 – 2 соs²α

Ответ:1 – 2 соs²α.

Задание. Упростите дробь

9hgfjui

Решение.

10jhlkl

Ответ: ctg⁶α.

Тригонометрические функции суммы и разности

Легко проводить вычисления, когда все тригонометрические действия выполняются над одним углом α. Однако иногда в задачах добавляется ещё один угол, который обычно обозначают как β. Существуют ф-лы, с помощью которых можно вычислять тригон-кие ф-ции от суммы и разности углов α и β.

Вывод этих ф-л достаточно сложен, поэтому сначала мы просто без доказательства приведем две из них, позволяющие вычислять синус суммы и косинус суммы:

11gfhgh

Достаточно запомнить их, а далее следующие формулы можно выводить из них. Так, если вместо β подставить угол (–β), то получим формулы для разности. При этом мы используем тот факт, что синус – нечетная ф-ция, то естьsin (– β) = – sinβ, а косинус – четная ф-ция, то есть соs (– β) = соsβ:

12fghgh

Теперь поступим также с ф-лой для косинуса разности:

Итак, нам удалось получить ф-лы для нахождения синуса и косинуса суммы и разности углов.

14ghgfj

С помощью этих формул возможно вычислить значение тригон-ких ф-ций для некоторых нестандартных углов. (Стандартными считаются углы в 0°, 30°, 45°, 60° и 90°, ведь для них значение тригон-ких ф-ций можно узнать из таблички.)

Задание. Вычислите соs 150°.

Решение. В табличке стандартных углов есть углы, равные 90° и 60°. Их сумма как раз равна 150°. Поэтому запишем:

15hgfh

Задание. Вычислите синус, косинус и тангенс для угла 15°.

Решение. Угол в 15° можно представить как разность 45° – 30°. Тогда синус будет вычисляться так:

16hgfh

Далее вычислим косинус:

17jhk

Можно выполнить проверку. Полученные значения должны удовлетворять основному тригон-кому тождеству. И действительно:

18hgj

Проверка пройдена: сумма квадратов синуса и косинуса оказалась равной единице. Теперь посчитаем tg 15°, используя определение тангенса:

19kjhk

Задание. Вычислите значение тригонометрического выражения

sinπ/7 соsπ/42 + sinπ/42 соsπ/7

Решение: Значение тригон-ких ф-ций для углов π/7 и π/42 мы не знаем, однако это не помешает вычислениям. Можно заметить, что исходное выражение представляет собой синус суммы π/7 и π/42:

sinπ/7 соsπ/42 + sinπ/42 соsπ/7 = sin (π/7 + π/42) = sinπ/6 = 1/2

Ответ: 1/2.

Задание. Упростите выражение

20jghj

Решение.

Вынесем за скобки множитель 2:

21fdfgf

Теперь произведем замену:

22hgf

C учетом этого можно переписать выражение и использовать ф-лу суммы косинусов:

23gfhj

Ответ: 2соs (π/6 + α).

Формулы двойного угла

Что будет, если формулу синуса суммы подставить не два различных угла α и β, а два одинаковых угла α и α? Получится ф-ла для синуса двойного угла:

24jhghj

Аналогично можно составить ф-лу и для косинуса двойного угла:

25jhghj

Итак, справедливы следующие ф-лы:

26kjhjk

Задание. Вычислите sin 120° и соs 120°.

Решение.

27jhgk

Задание. Упростите выражение

соs²t– соs 2t

Решение.

соs²t – соs 2t = соs²t – (соs²t – sin²t) = соs²t – соs²t + sin²t = sin²t

Ответ: sin²t.

Задание. Докажите, что функция

28hfgyu

является периодической и имеет период, равный π.

Решение. Используем ф-лу квадрата суммы:

29kjhf

Таким образом, исходную ф-цию можно переписать в виде

у = 1 + sin 2x

По определению, ф-ция является периодической с периодом Т, если выполняется условие у(х + Т) = у(х). Поэтому подставим в нашу ф-цию величину х + π:

30gfhyu

Получили, что у(х + π) = y(x), то есть ф-ция имеет период, равный π.

Задание. Выведите формулы синуса и косинуса тройного угла.

Решение. Для их получения следует использовать ф-лу синуса суммы углов, в которую подставляют вместо β величину 2α:

31gfdg

Аналогично можно получить и ф-лу для косинуса тройного угла:

32hgfj

Формулы понижения степени

Если нам необходимо узнать косинус угла, который вдвое больше табличного, мы используем ф-лу:

соs 2α = соs²α – sin²α

А что делать, если нам надо вычислить косинус угла, который вдвое меньше известного? Попробуем преобразовать ф-лу косинуса двойного угла:

33hgfhg

В результате нам удалось получить тождество, позволяющее по косинусу удвоенного угла найти косинус самого угла! Однако значительно чаще в тригонометрии это равенство записывают в обратном порядке:

34ghhgj

и называют ф-лой понижения степени. Действительно, в левой части стоит косинус в квадрате, а справа – косинус без квадрата, но вычисляется он от угла 2α, а не α.

Попробуем получить аналогичную ф-лу и для синуса. Для этого используем основное тригон-кое тождество:

35jhghj

36hghj

С помощью этих ф-л можно вычислять тригон-кие ф-ции для некоторых малых углов. Так, ранее мы с использованием ф-лу разности синусов определили, что

37hgfhg

При этом мы представляли угол 15° как разность 45° – 30°. Но как посчитать соs 7,5°? Этот угол невозможно представить как разницу или сумму известных нам табличных углов (0°, 30°; 45°; 60° и 90°). Однако поможет ф-ла понижения степени. Действительно, ведь 2•7,5° = 15°. Тогда можно записать:

Мы нашли соs² 7,5°. Чтобы узнать соs 7,5°, необходимо извлечь квадратный корень:

39khju

Так как угол 7,5° принадлежит I четверти, то его косинус должен быть положительным, поэтому можно записать:

40gdfh

Видно, что получается довольно громоздкое выражение. Используя ф-лу понижения степени, можно найти косинус и угла, который ещё вдвое меньше, то есть равен 3,75°, но в результате получится ещё более громоздкое выражение.

Задание. Вычислите sinπ/8.

Решение. Угол π/4 является табличным (его градусная мера составляет 45°). Поэтому можно записать:

41gfdfg

Эти примеры показывают, что тригон-кие ф-ции многих нестандартных углов можно выразить, используя квадратные корни. Возникает вопрос – а любую ли тригонометрическую ф-цию можно выразить таким способом? Оказывается, что нет. Например, sin 10° невозможно найти ни в одной, даже самой подробной тригонометрической таблице. Мы не будем это доказывать, но эту величину невозможно представить в виде выражения, используя арифметические операции и корни. Однако существуют приближенные методы, позволяющие с любой наперед заданной точностью вычислять значение тригонометрических ф-ций.

Формулы приведения

Возможно, вы уже заметили, что синусы и косинусы принимают одинаковые значения в углах, чья сумма равна 90°. Например, sin30° = соs60° = 1/2, и при этом 30° + 60° = 90°. Также мы знаем, что sin 45° = соs 45° (45° + 45° = 90°) и sin60° = соs30° (60° + 30°). В чем причина такой закономерности и справедлива ли она для нестандартных углов?

Используя ф-лу синуса разности, мы можем записать, что

Полученная ф-ла sin (90° – α) = соsα называется формулой приведения. При ее выводе мы использовали тот факт, что sin 90° = 1, а соs 90° = 0, поэтому формула получилась очень простой. Однако синусы и косинусы других углов, кратных 90° (или кратных π/2, если измерять углы в радианах), также равны 0, 1 или – 1, поэтому для них тоже можно получить подобные простые ф-лы, например:

Похожих ф-л можно написать несколько десятков! Все их запоминать не надо, так как существует особое мнемоническое правило, позволяющее записать необходимую ф-лу.

Пусть есть некоторое тригон-кое выражение вида

f(k ± α)

где f – тригонометрическая ф-ция (sin; соs; tg; ctg)

k– угол, кратный π/2 (π/2, π, 3π/2, 2π)

Мы хотим заменить ее другой ф-цией, только от угла α. На первом шаге мы смотрим на слагаемое k. Если оно кратно π (– π, π, 2π), то ф-ция f остается неизменной. Если же слагаемое k – это число π/2 или 3π/2, то ф-цию f надо поменять на так называемую кофункцию (синус меняем на косинус, тангенс на котангенс и наоборот).

Далее надо определить знак, стоящий перед новой ф-цией. Для этого мы предполагаем, что α – это острый угол, то есть он принадлежит I четверти. Далее с учетом этого предположения смотрим, в какую четверть попадает угол k ± α, и какое значение принимает там исходная тригонометрическая ф-ция. Если она отрицательна, то перед новой тригонометрической ф-цией надо поставить минус. В противном случае ничего ставить не надо.

Лучше всего изучить это алгоритм на примерах.

Задание. Упростите выражение соs (π/2 + α).

Решение. Первый шаг – смотрим на слагаемое под знаком косинуса. Это число π/2. Оно НЕ кратно π, а потому мы должны поменять косинус на синус:

sinα

Второй шаг – надо определить, надо ли ставить минус перед синусом. Если α – это острый угол, то угол (π/2 + α) попадет во II четверть:

44gfyj

Во второй четверти косинус отрицателен, а потому перед синусом следует поставить минус:

соs (π/2 + α) = – sinα

Ответ: – sinα.

Важное примечание. В этом примере для составления формулы приведения мы «предположили», что угол α является острым. В результате нам удалось получить формулу соs (π/2 + α) = – sinα. Однако отметим, что полученная нами формула выполняется для абсолютно любых значений угла α, а не только для 0° < α < 90°. Предположение об остроте угла – это лишь часть мнемонического правила для составления формул приведения, позволяющая быстро определить, надо ли в ней перед тригонометрической функцией ставить знак минус или не надо.

Это мнемоническое правило работает абсолютно точно, однако надо понимать, что всё-таки для строгого вывода формул приведения следует использовать формулу косинуса суммы

соs (π/2 + α) = cosπ/2 cos α – sin π/2 sin α = 0•cos α – 1•sin α = – sin α

Получили тот же результат, что и с помощью формулы приведения. При этом нам не потребовалось предположение об остроте угла α, то есть формула верна для любых α. Но практика показывает, что люди просто не могут запомнить формулу косинусов суммы. Поэтому для «упрощения жизни» школьникам рассказывают об относительно простом мнемоническом правиле.

Задание. Составьте ф-лу приведения для выражения tg (α – π).

Решение. Сначала смотрим на слагаемое под знаком тангенса. Это число (– π), кратное π. Поэтому сама ф-ция не меняется на кофункцию:

tgα

Примем, что угол α принадлежит I четверти, тогда угол α – π будет ему противоположен и окажется в III четверти:

45hgdh

Тангенс в III четверти положителен. Значит, минуса перед тангенсом ставить не надо:

tg (α– π) = tgα

Задание. Вычислите sin 7π/6.

Решение. Представим угол 7π/6 как сумму: 7π/6 = π + π/6. Получается, нам надо вычислить величину sin (π + π/6). Составим ф-лу приведения для выражения π + α Так как в скобках стоит слагаемое π, то ф-ция sin остается, а не меняется на косинус:

sinα

Угол (π + α) относится к III четверти, где синус отрицателен. Следовательно, надо добавить знак минус:

sin (π + α) = – sinα

Остается подставить вместо α величину π/6:

sin (π + π/6) = – sinπ/6 = – 1/2

Ответ: – 1/2.

Задание. Чему равен ctg7π/4?

Решение. Угол 7π/4 можно представить как 3π/2 + π/4. Найдем ф-лу приведения для ctg (3π/2 + α). Из-за слагаемого 3π/2, не кратного π, ф-ция должна измениться с котангенса на тангенс:

ctg (3π/2 + α) = tgα

Угол 3π/2 + α попадает в IV четверть, где котангенс отрицателен. Поэтому необходимо добавить знак минуса перед ф-цией:

ctg (3π/2 + α) = –tgα

Ф-ла приведения получена. Осталось подставить в неё значение α = π/4:

ctg (7π/4) = ctg (3π/2 + π/4) = – tgπ/4 = – 1

Ответ: – 1.

Откуда же возникло название «формула приведения»? Дело в том, что с их помощью вычисление тригонометрических ф-ций от углов из диапазона 0 ≤ π ≤ 2π можно привести к вычислению ф-ций от углов из I четверти, то есть из диапазона 0 ≤ α ≤ π/2. Это означает, что нет смысла заучивать большие таблицы, в которых указаны синусы и косинусы углов, больших 90°. Достаточно знать ф-ции от стандартных углов: 0, π/6; π/4, π/3 и π/2.

Если всё же использование ф-л приведения вызывает сложности, то вместо них всегда можно использовать обычные ф-лы косинуса и синуса суммы, которые дадут такой же результат.

В прошлом уроке, строя графики косинуса, мы заметили, что он представляет собой синусоиду, смещенную на π/2 единиц:

46hgfgh

Теперь становится ясна причина этого смещения. Дело в ф-ле приведения

соsx = sin (x + π/2)

Она показывает, что точки графика косинуса могут быть получены параллельным переносом точек синусоиды на π/2 единиц влево.

Сумма тригонометрических функций

Мы видим, что тригон-ких формул довольно много. Надо ли все их учить? Этого делать не надо. Достаточно иметь под рукой справочник при решении задач, связанных с преобразованием тригонометрических выражений, в котором все эти ф-лы можно посмотреть. В крайнем случае можно всегда самостоятельно вывести все ф-лы, используя только основное тригон-кое тождество и ф-лы синуса и косинуса суммы. Они, кстати, выдаются в качестве раздаточного материала учащимся при сдаче ЕГЭ. Ещё важно помнить определение тангенса, которое в раздаточном материале не записано.

Пусть есть два произвольных угла s и t. Найдем синусы их разности и суммы:

Сложим эти два уравнения:

48hfgh

Теперь произведем замену. Будем считать, что

x = s + t

у = s – t

Это значит, чтох + у = 2s, или

s = (x + y)/2

С другой стороны

х – у = s + t– (s– t) = 2t

то есть

t = (x – у)/2

Подставляем всё это в ф-лу (1):

49hgfhy

Получили формулу, с помощью которой можно найти сумму любых двух синусов! Теперь попытаемся составить аналогичную ф-лу и для их разности синусов. При этом мы учтем нечетность синуса (это значит, что sin (– у) = – sinу):

50hfgj

51gfjhj

Задание. Упростите выражения

52gfhj

Решение.

53hgfh2

Теперь попробуем составить ф-лы для сложения и вычитания косинусов. Для этого запишем ф-лы для произвольных величин s и t:

54gfjhj

Сложив уравнения, мы получим тождество

Далее произведем замены, которые выполняли и ранее:

x = s + t

у = s – t

s = (x + y)/2

t = (x – у)/2

Подставляя всё это в (3), получим:

56jkgjk

Получили ф-лу, с помощью которой можно складывать косинусы. Чтобы их можно было вычитать, вычтем из (1) уравнение (2):

57jhkjk

Снова произведем замены переменных s и t:

58hgfhf

Получили ф-лу и для разности косинусов.

Задание. Упростить тригонометрические выражения

60hgfgh

Решение.

в) Здесь мы сталкиваемся с более сложным случаем, так как из косинуса надо вычесть синус. У нас нет готовой ф-лы для такого действия. Однако вспомним, что с помощью формул приведения легко заменить синус на косинус:

sinx = соs (π/2 – х)

Тогда исходное выражение уже можно будет преобразовать:

62hgjhj

Произведение тригонометрических функций

В предыдущем разделе, когда мы выводили ф-лы для вычисления суммы синусов и косинусов, мы сначала получали уравнения:

63jhgk

Далее мы производили замену переменных sи t. Однако давайте вместо этого просто поделим первые два уравнения на двойку, а третье – на (– 2):

64hfgh

В случае с последней формулой мы воспользовались правилом, по которому знак минус перед дробью можно убрать, если в числителе поменять местами вычитаемое и уменьшаемое.

Получили ф-лы, которые позволяют заменять произведение тригонометрических ф-ций их суммой.

65hgkjk

Задание. Преобразуйте произведение в сумму:

66hjh

Решение.

67gdfgd

На этом наше знакомство с основными тригонометрическими формулами заканчивается. Ещё раз напомним, что в рамках школьного курса заучивать все ф-лы не нужно, можно при необходимости пользоваться смотреть в справочник. Тригон-кие преобразования помогут в будущем при решении сложных тригон-ких уравнений.

В самом конце приведем перечень всех формул, выведенными в этом уроке:

Источник

Интеграл Фурье

Комплексная форма интеграла Фурье

Преобразование Фурье. Косинус- и синус-преобразования Фурье

Косинус- и синус-преобразования Фурье

Амплитудный и фазовый спектры интеграла Фурье

Свойства преобразования Фурье

Приложения преобразования Фурье

Понятие о многомерном преобразовании Фурье

Дополнение к преобразованию Фурье

Определение[править | править код]

Синус-преобразование Фурье[править | править код]

Косинус-преобразование Фурье[править | править код]

Обратное синус- и косинус-преобразование Фурье[править | править код]

Расширение на комплексные числа[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Простейшие тригонометрические тождества

Преобразование отрицательных углов тригонометрических функций (четность и нечетность)

Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)

Формулы универсальной тригонометрической подстановки

Тригонометрические тождества преобразования половины угла

Тригонометрические формулы сложения углов

Формулы преобразования суммы или разности тригонометрических функций

Формулы тройного угла – преобразование sin3α cos3α tg3α в sinα cosα tgα

Формулы преобразования произведения тригонометрических функций

Формулы приведения тригонометрических функций

Основное тригонометрическое тождество

Тригонометрические функции суммы и разности

Формулы двойного угла

Формулы понижения степени

Формулы приведения

Сумма тригонометрических функций

Произведение тригонометрических функций

Вам также может понравиться

Как найти человека который попал в полицию

Windows 10 как найти папку мой компьютер

Dying light the following тайники как найти

Добавить комментарий Отменить ответ