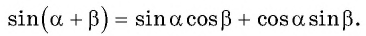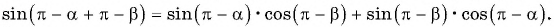Формулы суммы и разности углов тригонометрических функций онлайн
С помощю этого онлайн калькулятора можно получить формулы суммы и разности углов тригонометрических функций. Для получения формулы выберите нужную тригонометрическую функцию, нажав на “sin”, выберите нужный аргумент, нажав на аргумент в формуле. В результате получится формула для этой функции и аргумента. Теоретическую часть и численные примеры смотрите ниже.
Формулы суммы и разности углов тригонометрических функций − теория, доказательство, примеры
Выведем формулы суммы и разности углов тригонометрических функций. Начнем с формулы
Как мы знаем, угол между векторами не может быть больше 180° (π). На рисунке Рис.1 угол между векторами  и
и  равен
равен  . На рисунке Рис.2 угол между векторами
. На рисунке Рис.2 угол между векторами  и
и  равен
равен  .
.
Рассмотрим, теперь косинусы этих углов. Из формул приведения мы знаем (подпрбнее о формулах приведения смотрите на странице Формулы приведения тригонометрических функций онлайн):
Cкалярное произведение векторов  и
и  равно:
равно:
Так как точка  имеет координаты
имеет координаты  , а
, а  имеет координаты
имеет координаты  (смотрите статью на странице Синус и косинус. Онлайн калькулятор), то скалярное произведения векторов
(смотрите статью на странице Синус и косинус. Онлайн калькулятор), то скалярное произведения векторов  и
и  по координатам равно:
по координатам равно:
Поскольку левые части формул (2) и (3) равны, то равны и правые части этих формул. Следовательно выполнено равенство (1).
Докажем, далее, справедливость следующей формулы
Представим косинус суммы углов α и β в виде косинуса разности двух углов и воспользуемся формулой (1) и тем, что косинус четная функция а синус нечетная функция:
Перейдем к доказательству формул синусов суммы и разности углов:
Для доказательства формулы (5) воспользуемся формулами приведения тригонометрических функций и формулой (1):
Для доказательства формулы (6), представим разность углов в виде суммы и воспользуемся тем, что косинус четная функция а синус нечетная функция:
Формулы тангенса суммы и разности углов имееют следующий вид:
Докажем формулу (7):
Разделим числитель и знаменатель дроби в правой части уравнения (9) на  (
( ,
,  ):
):
Для доказательства формулы (9) представим разность углов в виде суммы, воспользуемся формулой (8) и учтем, что тангенс нечетная функция:
Формулы котангенса суммы и разности углов имееют следующий вид:
Докажем формулу (10):
Разделим числитель и знаменатель дроби в правой части уравнения (12) на  (
( ,
,  ):
):
Для доказательства формулы (11), представим разность углов α и β в виде суммы и учтем, что котангенс нечетная функция:
Умножив числитель и знаменатель в правой части уравнения (13) на −1, получим формулу (11).
Примеры использования формул суммы и разности углов тригонометрических функций
Пример 1. Найти точное значение  .
.
Решение:
Ответ:
Пример 2. Найти косинус для угла 15°.
Решение:
Ответ:
Пример 3. Найти точное значение тангенса для угла 15° .
Решение:
Тангенсы для углов 45° и 15° известны. Подставим эти значения в (14):
Дробь в правой части уравнения (15) можно упростить, умножив числитель и знаменатель дроби на  :
:
Ответ:
Основные тригонометрические формулы
Содержание
 Связи между тригонометрическими функциями одного угла Связи между тригонометрическими функциями одного угла |
 Тригонометрические функции суммы и разности двух углов Тригонометрические функции суммы и разности двух углов |
 Тригонометрические функции двойного угла Тригонометрические функции двойного угла |
 Формулы понижения степени для квадратов тригонометрических функций Формулы понижения степени для квадратов тригонометрических функций |
 Формулы понижения степени для кубов синуса и косинуса Формулы понижения степени для кубов синуса и косинуса |
 Выражение тангенса угла через синус и косинус двойного угла Выражение тангенса угла через синус и косинус двойного угла |
 Преобразование суммы тригонометрических функций в произведение Преобразование суммы тригонометрических функций в произведение |
 Преобразование произведения тригонометрических функций в сумму Преобразование произведения тригонометрических функций в сумму |
 Выражение тригонометрических функций через тангенс половинного угла Выражение тригонометрических функций через тангенс половинного угла |
 Тригонометрические функции тройного угла Тригонометрические функции тройного угла |
![]()
Связи между тригонометрическими функциями одного угла
Тригонометрические функции суммы и разности двух углов
Тригонометрические функции двойного угла
| Формула | Название формулы |
| sin 2α = 2 sin α cos α | Синус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
Косинус двойного угла |
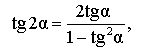 |
Тангенс двойного угла |
| Синус двойного угла |
| sin 2α = 2 sin α cos α |
| Косинус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
| Тангенс двойного угла |
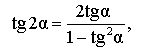 |
Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
|
Выражение квадрата синуса через косинус двойного угла |
|
|
Выражение квадрата косинуса через косинус двойного угла |
|
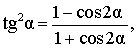 |
Выражение квадрата тангенса через косинус двойного угла |
Формулы понижения степени для кубов синуса и косинуса
| Формула | Название формулы |
|
Выражение куба синуса через синус угла и синус тройного угла |
|
|
Выражение куба косинуса через косинус угла и косинус тройного угла |
|
Выражение куба синуса через синус угла и синус тройного угла |
|
Выражение куба косинуса через косинус угла и косинус тройного угла |
Выражение тангенса через синус и косинус двойного угла
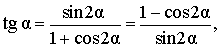

Преобразование суммы тригонометрических функций в произведение
| Сумма синусов |
|
|
| Разность синусов |
|
|
| Сумма косинусов |
|
|
| Разность косинусов |
|
|
| Сумма тангенсов |
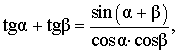 |
| Разность тангенсов |
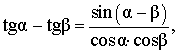 |
Преобразование произведения тригонометрических функций в сумму
| Произведение синусов |
|
|
| Произведение косинусов |
|
|
| Произведение синуса и косинуса |
|
|
Выражение тригонометрических функций через тангенс половинного угла
| Формула | Название формулы |
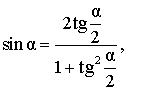 |
Выражение синуса угла через тангенс половинного угла |
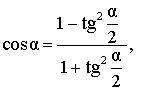 |
Выражение косинуса угла через тангенс половинного угла |
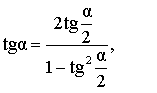 |
Выражение тангенса угла через тангенс половинного угла |
Тригонометрические функции тройного угла
| Формула | Название формулы |
| sin 3α = 3sin α – 4sin3α | Синус тройного угла |
| cos 3α = 4cos3α –3cos α | Косинус тройного угла |
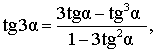 |
Тангенс тройного угла |
| Синус тройного угла |
| sin 3α = 3sin α – 4sin3α |
| Косинус тройного угла |
| cos 3α = 4cos3α –3cos α |
| Тангенс тройного угла |
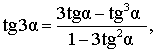 |
Содержание:
Известные значения синуса, косинуса, тангенса углов можно использовать для вычисления значений синуса, косинуса, тангенса других углов.
Угол 
Выведем формулу 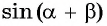 — синуса суммы двух углов. Рассмотрим случай, когда
— синуса суммы двух углов. Рассмотрим случай, когда  — острые углы в треугольнике
— острые углы в треугольнике  (рис. 115).
(рис. 115). 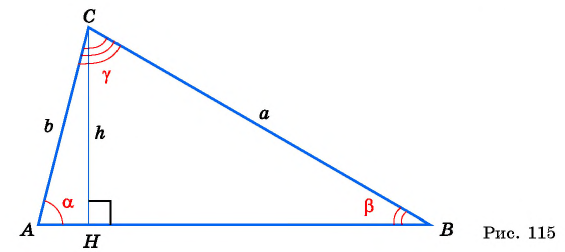
Выразим площадь треугольника  дважды:
дважды:
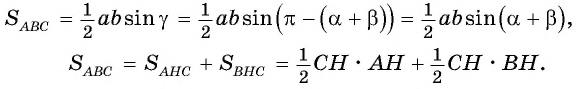
Треугольник 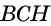 — прямоугольный, тогда
— прямоугольный, тогда 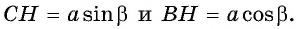 Из прямоугольного треугольника
Из прямоугольного треугольника 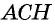 имеем:
имеем: 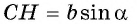 и
и 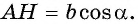 Тогда
Тогда
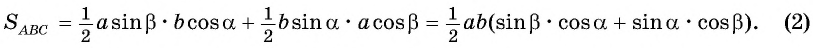
Приравняем правые части равенств (1) и (2):
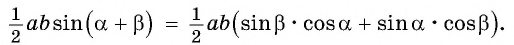
Разделим обе части равенства на 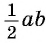 и получим формулу синуса суммы двух углов:
и получим формулу синуса суммы двух углов:
Если углы 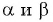 не являются острыми, то можно воспользоваться свойством периодичности синуса и формулами приведения.
не являются острыми, то можно воспользоваться свойством периодичности синуса и формулами приведения.
Например, если 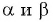 являются углами второй четверти, то
являются углами второй четверти, то 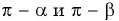 — острые углы.
— острые углы.
Применим к ним выведенную для острых углов формулу синуса суммы:
Воспользуемся формулами приведения в левой части равенства (3) и получим: 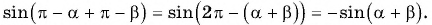
Применим формулы приведения к правой части равенства (3): 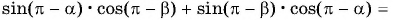
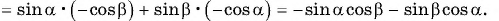
Таким образом,
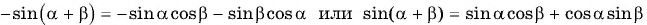 — формула синуса суммы двух углов.
— формула синуса суммы двух углов.
Остальные случаи принадлежности углов различным четвертям рассматриваются аналогично предыдущему.
Синус суммы
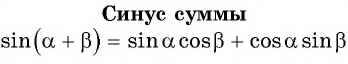
Воспользуемся полученной формулой 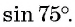
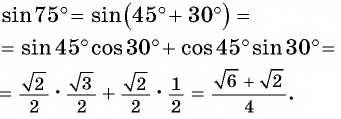
Выведем формулу синуса разности двух углов.
Для этого 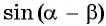 представим в виде
представим в виде 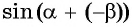 и применим формулу синуса суммы двух углов:
и применим формулу синуса суммы двух углов:
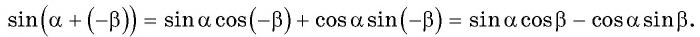
Получили формулу синуса разности двух углов:
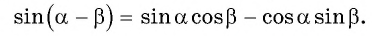
Синус разности
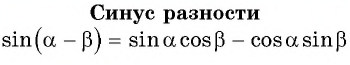
Вычислим, например, 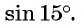
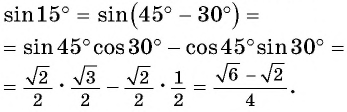
Для вывода формулы косинуса суммы двух углов воспользуемся формулами приведения и получим: 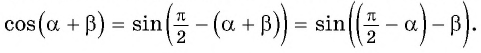
Тогда по формуле синуса разности двух углов имеем:
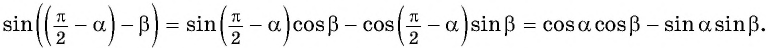
Получили формулу косинуса суммы двух углов:
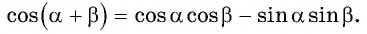
Косинус суммы

Применим полученную формулу и вычислим, например, 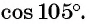
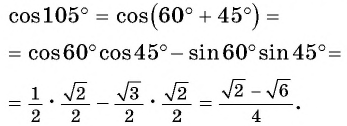
Представив разность  в виде суммы
в виде суммы 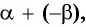 можно получить формулу косинуса разности двух углов:
можно получить формулу косинуса разности двух углов: 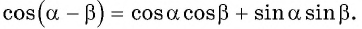
Косинус разности
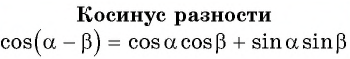 Найдем, например,
Найдем, например, 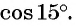
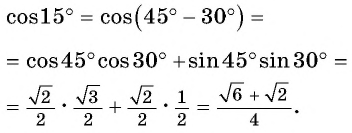
Пример №1
Вычислите:
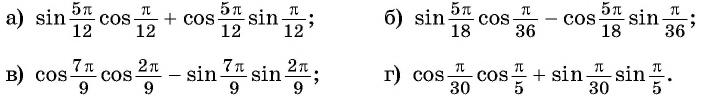
Решение:
Применим полученные формулы «справа налево»: 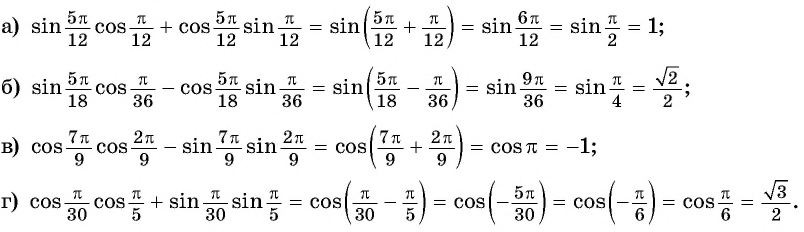 Выведем формулы тангенса суммы и тангенса разности двух углов.
Выведем формулы тангенса суммы и тангенса разности двух углов.
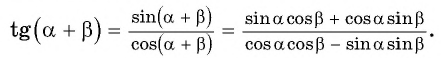 Разделим числитель и знаменатель дроби на
Разделим числитель и знаменатель дроби на 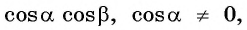
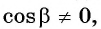 тогда:
тогда:
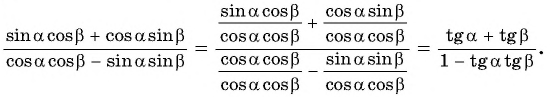
Таким образом, получили формулу тангенса суммы двух углов:
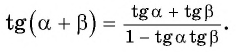
Воспользуемся формулой тангенса суммы и вычислим, например, 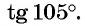
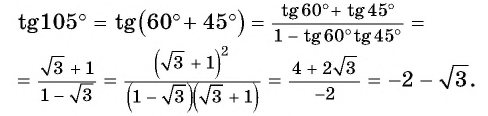
Тангенс суммы
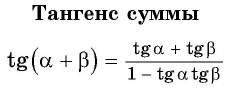 Представив разность
Представив разность 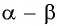 в виде суммы
в виде суммы 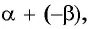 можно получить формулу тангенса разности двух углов:
можно получить формулу тангенса разности двух углов:
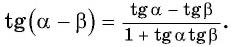 Найдем, например,
Найдем, например, 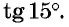
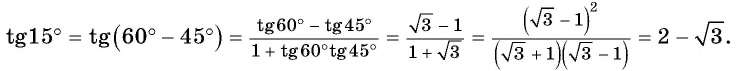
Тангенс разности
Пример №2
Вычислите:
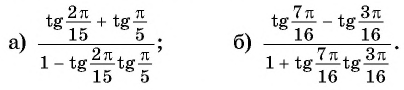
Решение:
Применим формулы тангенса суммы и тангенса разности «справа налево»:
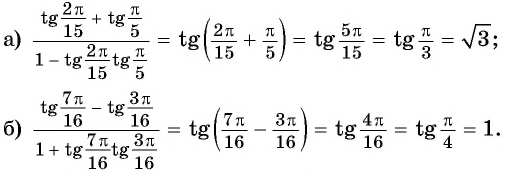
Полученные формулы синуса суммы, синуса разности, косинуса суммы, косинуса разности, тангенса суммы, тангенса разности двух углов называют формулами сложения.
Примеры заданий и их решения
Пример №3
С помощью формул сложения преобразуйте выражение:

Решение:
а) По формуле синуса разности получим:
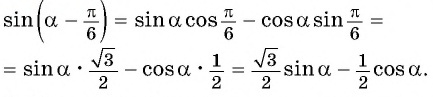
б) Применим формулу тангенса суммы:
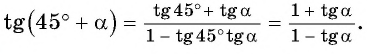
Пример №4
Найдите значение выражения:
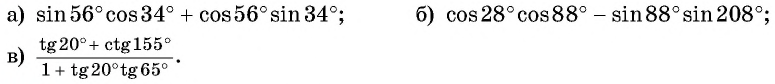
Решение:
а) По формуле синуса суммы получим:
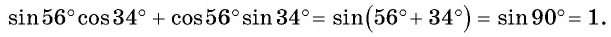
б) По формулам приведения получим, что 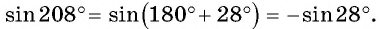
Тогда 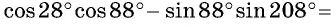
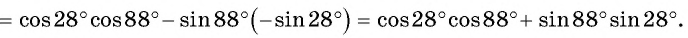 Воспользуемся формулой косинуса разности и получим:
Воспользуемся формулой косинуса разности и получим:
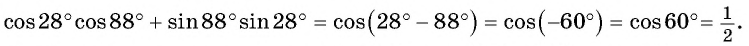
в) По формулам приведения 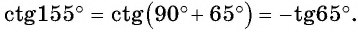
Тогда 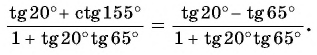
По формуле тангенса разности:
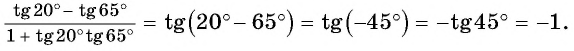
Пример №5
Вычислите:

Решение:
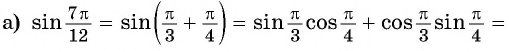
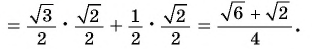
б) По формулам приведения: 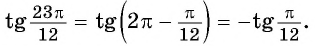
По формуле тангенса разности получим:
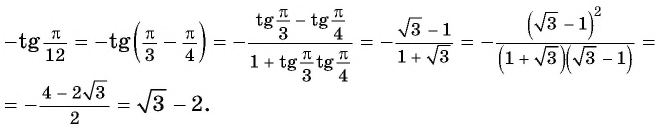
Таким образом, 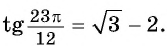
- Заказать решение задач по высшей математике
Пример №6
Упростите выражение:
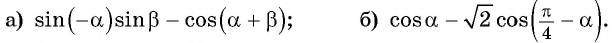
Решение:
а) Воспользуемся нечетностью синуса и формулой косинуса разности:
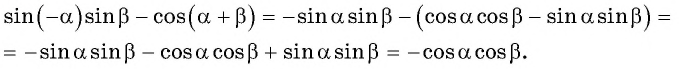
б) Применим формулу косинуса разности и получим: 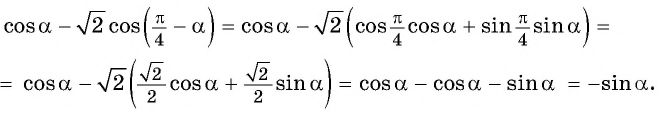
Пример №7
Решите уравнение 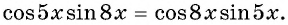
Решение:
Запишем уравнение в виде 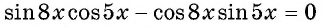 и по формуле синуса разности получим:
и по формуле синуса разности получим: 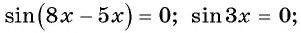
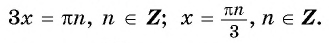
Ответ: 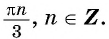
Пример №8
Вычислите 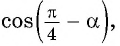 если
если 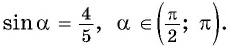
Решение:
Применим формулу косинуса разности:
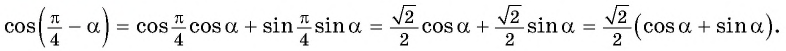
Из основного тригонометрического тождества выразим 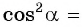
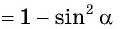 и найдем
и найдем 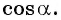 Так как
Так как 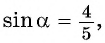 то
то 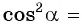
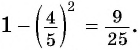 Значит,
Значит, 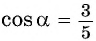 или
или 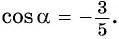 Поскольку
Поскольку 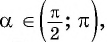 т. е.
т. е. 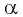 угол второй четверти, то
угол второй четверти, то 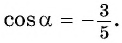 Тогда
Тогда
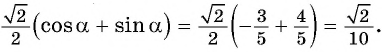
Пример №9
Докажите тождество 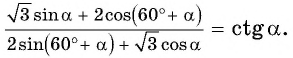
Решение:
Воспользуемся формулами сложения и получим:
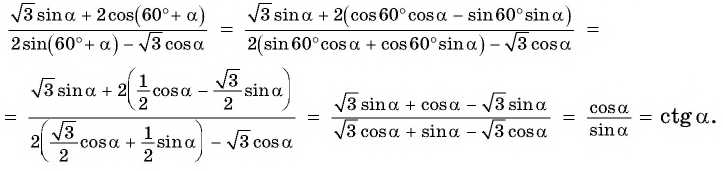
Пример №10
Найдите значение выражения:
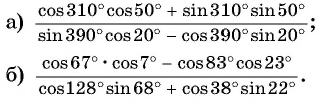
Решение:
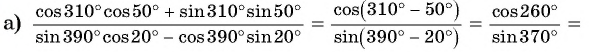
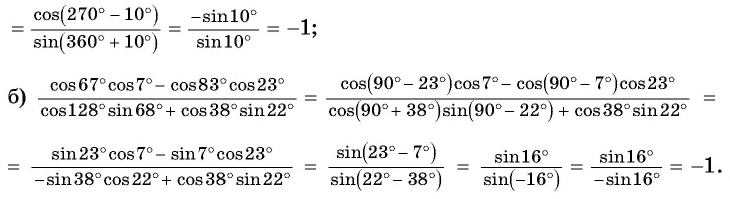 9.
9.
Пример №11
Найдите множество значений функции
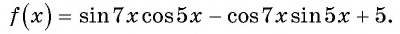
Решение:
Применим формулу синуса разности и запишем функцию в виде 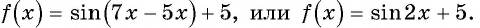
Так как 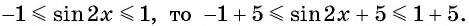 Таким образом, имеем:
Таким образом, имеем: 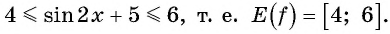
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
Наиболее часто встречающиеся тригонометрические формулы:
(blacktriangleright) Основные тождества: [begin{array}{|l|l|}
hline sin^2 alpha+cos^2 alpha =1& mathrm{tg}, alpha cdot
mathrm{ctg}, alpha =1 \
&(sinalphane 0, cosalphane 0)\[0.5ex]
hline &\
mathrm{tg}, alpha=dfrac{sin alpha}{cos alpha}
&mathrm{ctg}, alpha
=dfrac{cos alpha}{sin alpha} \&\
1+mathrm{tg}^2, alpha =dfrac1{cos^2 alpha} & 1+mathrm{ctg}^2, alpha=dfrac1{sin^2 alpha}\&\
(cosalphane 0)& (sinalphane 0) \
hline
end{array}]
(blacktriangleright) Формулы сложения углов: [begin{array}{|l|r|}
hline &\
sin{(alphapm beta)}=sinalphacdot cosbetapm sinbetacdot
cosalpha & cos{(alphapm beta)}=cosalphacdot cosbeta mp
sinalphacdot sinbeta\ &\
hline &\
mathrm{tg}, (alphapm beta)=dfrac{mathrm{tg}, alphapm
mathrm{tg}, beta}{1 mp mathrm{tg}, alphacdot
mathrm{tg}, beta} & mathrm{ctg}, (alphapmbeta)=-dfrac{1mp mathrm{ctg}, alphacdot mathrm{ctg}, beta}{mathrm{ctg}, alphapm mathrm{ctg}, beta}\&\
cosalphacosbetane 0&sinalphasinbetane 0\
hline
end{array}]
(blacktriangleright) Формулы двойного и тройного углов: [begin{array}{|lc|cr|}
hline sin {2alpha}=2sin alphacos alpha & qquad &qquad & cos{2alpha}=cos^2alpha -sin^2alpha\
sin alphacos alpha =dfrac12sin {2alpha} && & cos{2alpha}=2cos^2alpha -1\
& & & cos{2alpha}=1-2sin^2 alpha\
hline &&&\
mathrm{tg}, 2alpha = dfrac{2mathrm{tg},
alpha}{1-mathrm{tg}^2, alpha} && & mathrm{ctg}, 2alpha
= dfrac{mathrm{ctg}^2, alpha-1}{2mathrm{ctg}, alpha}\&&&\
cosalphane 0, cos2alphane 0 &&& sinalphane 0,
sin2alphane 0\
hline &&&\
sin {3alpha}=3sin alpha -4sin^3alpha && &
cos{3alpha}=4cos^3alpha -3cos alpha\&&&\
hline
end{array}]
(blacktriangleright) Формулы понижения степени: [begin{array}{|lc|cr|}
hline &&&\
sin^2alpha=dfrac{1-cos{2alpha}}2 &&&
cos^2alpha=dfrac{1+cos{2alpha}}2\&&&\
hline
end{array}]
(blacktriangleright) Формулы произведения функций: [begin{array}{|c|}
hline \
sinalphasinbeta=dfrac12bigg(cos{(alpha-beta)}-cos{(alpha+beta)}bigg)\\
cosalphacosbeta=dfrac12bigg(cos{(alpha-beta)}+cos{(alpha+beta)}bigg)\\
sinalphacosbeta=dfrac12bigg(sin{(alpha-beta)}+sin{(alpha+beta)}bigg)\\
hline
end{array}]
(blacktriangleright) Формулы суммы/разности функций: [begin{array}{|lc|cr|}
hline &&&\
sinalpha+sinbeta=2sin{dfrac{alpha+beta}2}cos{dfrac{alpha-beta}2}
&&&
sinalpha-sinbeta=2sin{dfrac{alpha-beta}2}cos{dfrac{alpha+beta}2}\&&&\
cosalpha+cosbeta=2cos{dfrac{alpha+beta}2}cos{dfrac{alpha-beta}2}
&&& cosalpha
-cosbeta=-2sin{dfrac{alpha-beta}2}sin{dfrac{alpha+beta}2}\&&&\
mathrm{tg}, alpha pm mathrm{tg},
beta=dfrac{sin{(alphapmbeta)}}{cosalphacosbeta} &&&
mathrm{ctg}, alphapm mathrm{ctg}, beta= – dfrac{sin{(alphapm beta)}}{sinalphasinbeta}\&&&\
hline
end{array}]
(blacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [begin{array}{|l|r|}
hline &\
sin{2alpha}=dfrac{2mathrm{tg}, alpha}{1+mathrm{tg}^2, alpha} & cos{2alpha}=dfrac{1-mathrm{tg}^2, alpha}{1+mathrm{tg}^2, alpha}\&\
cosalphane 0 & sinalphane 0\
hline
end{array}]
(blacktriangleright) Формула вспомогательного аргумента: [begin{array}{|c|}
hline text{Частный случай}\
hline \
sinalphapm cosalpha=sqrt2cdot
sin{left(alphapm dfrac{pi}4right)}\\
sqrt3sinalphapm cosalpha=2sin{left(alphapm dfrac{pi}6right)}\\
sinalphapm sqrt3cosalpha=2sin{left(xpm dfrac{pi}3right)}\\
hline text{Общий случай}\
hline\
asinalphapm bcosalpha=sqrt{a^2+b^2}cdot sin{(alphapm
phi)}, cosphi=dfrac a{sqrt{a^2+b^2}}, sinphi=dfrac
b{sqrt{a^2+b^2}}\\
hline
end{array}]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
(blacktriangleright) Вывод формулы косинуса разности углов (cos{(alpha
-beta)}=cosalphacosbeta+sinalphasinbeta)
Рассмотрим тригонометрическую окружность и на ней углы (alpha) и (beta). Пусть этим углам соответствуют точки (A) и (B) соответственно. Тогда координаты этих точек: (A(cosalpha;sinalpha), B(cosbeta;sinbeta)).
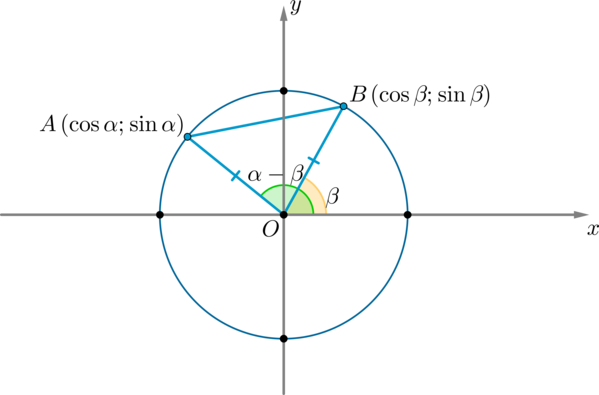
Рассмотрим (triangle AOB: angle AOB=alpha-beta). По теореме косинусов:
(AB^2=AO^2+BO^2-2AOcdot BOcdot
cos(alpha-beta)=1+1-2cos(alpha-beta) (1)) (т.к. (AO=BO=R) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
(AB^2=(cosalpha-cosbeta)^2+(sinalpha-sinbeta)^2=cos^2alpha-2cosalphacosbeta+cos^2beta+)
(+sin^2alpha-2sinalphasinbeta+sin^2beta=big(cos^2alpha+sin^2alphabig)+big(cos^2beta+sin^2betabig)-2big(cosalphacosbeta+sinalphasinbetabig)=)
(=1+1-2big(cosalphacosbeta+sinalphasinbetabig) (2))
Таким образом, сравнивая равенства ((1)) и ((2)):
(1+1-2big(cosalphacosbeta+sinalphasinbetabig)=1+1-2cos(alpha-beta))
Отсюда и получается наша формула.
(blacktriangleright) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения (sin x=cos(90^circ-x)) и (cos x=sin (90^circ-x)):
1) (cos(alpha+beta)=cos(alpha-(-beta))=cosalphacos(-beta)+sinalphasin(-beta)=cosalphacosbeta-sinalphasinbeta)
2) (sin(alpha+beta)=cos(90^circ-(alpha+beta))=cos((90^circ-alpha)-beta)=)
(+cos(90^circ-alpha)cosbeta+sin(90^circ-alpha)sinbeta=sinalphacosbeta+cosalphasinbeta)
3) (sin(alpha-beta)=sin(alpha+(-beta))=sinalphacos(-beta)+sin(-beta)cosalpha=sinalphacosbeta-sinbetacosalpha)
4) (mathrm{tg},(alphapmbeta)=dfrac{sin (alphapmbeta)}{cos
(alphapmbeta)}=dfrac{sinalphacosbetapmsinbetacosalpha}{cosalphacosbetampsinalphasinbeta}=)
разделим числитель и знаменатель дроби на (cosalphacosbetane
0)
(при (cosalpha=0 Rightarrow
mathrm{tg},(alphapmbeta)=mp mathrm{ctg},beta), при (cosbeta=0 Rightarrow
mathrm{tg},(alphapmbeta)=pm mathrm{ctg},alpha)):
(=dfrac{mathrm{tg},alphapmmathrm{tg},beta}{1mpmathrm{tg},alphacdot
mathrm{tg},beta})
Таким образом, данная формула верна только при (cosalphacosbetane 0).
5) Аналогично, только делением на (sinalphasinbetane 0), выводится формула котангенса суммы/разности двух углов.
(blacktriangleright) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) (sin
2alpha=sin(alpha+alpha)=sinalphacosalpha+sinalphacosalpha=2sinalphacosalpha)
2) (cos2alpha=cos(alpha+alpha)=cosalphacosalpha-sinalphasinalpha=cos^2alpha-sin^2alpha)
Используя основное тригонометрическое тождество (sin^2alpha+cos^2alpha=1), получим еще две формулы для косинуса двойного угла:
2.1) (cos2alpha=cos^2alpha-sin^2alpha=cos^2alpha-(1-cos^2alpha)=2cos^2alpha-1)
2.2) (cos2alpha=cos^2alpha-sin^2alpha=(1-sin^2alpha)-sin^2alpha=1-2sin^2alpha)
3) (mathrm{tg},2alpha=dfrac{sin2alpha}{cos2alpha}=dfrac{2sinalphacosalpha}{cos^2alpha-sin^2alpha}=)
разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0 Rightarrow mathrm{tg},2alpha=0)):
(=mathrm{tg},2alpha=dfrac{2mathrm{tg},alpha}{1-mathrm{tg}^2,alpha})
Таким образом, эта формула верна только при (cosalphane 0), а также при (cos2alphane 0) (чтобы существовал сам (mathrm{tg},2alpha)).
4) (mathrm{ctg},2alpha=dfrac{cos^2alpha-sin^2alpha}{2sinalphacosalpha}=dfrac{mathrm{ctg}^2,alpha-1}{2mathrm{ctg},alpha})
По тем же причинам при (sinalphane 0, sin2alphane 0).
5) (sin3alpha=sin(alpha+2alpha)=sinalphacos2alpha+cosalphasin2alpha=sinalpha(1-2sin^2alpha)+cosalphacdot
2sinalphacosalpha=)
(=sinalpha-2sin^3alpha+2sinalpha(1-sin^2alpha)=3sinalpha-4sin^3alpha)
6) Аналогично выводится, что (cos3alpha=cos(alpha+2alpha)=4cos^3alpha-3cosalpha)
(blacktriangleright) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) (cos2alpha=2cos^2alpha-1 Rightarrow
cos^2alpha=dfrac{1+cos2alpha}2)
2) (cos2alpha=1-2sin^2alpha Rightarrow
sin^2alpha=dfrac{1-cos2alpha}2)
Заметим, что в данных формулах степень синуса/косинуса равна (2) в левой части, а в правой части степень косинуса равна (1).
(blacktriangleright) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
(cos(alpha-beta)=cosalphacosbeta+sinalphasinbeta)
(cos(alpha+beta)=cosalphacosbeta-sinalphasinbeta)
Получим: (cos(alpha+beta)+cos(alpha-beta)=2cosalphacosbeta
Rightarrow
cosalphacosbeta=dfrac12Big(cos(alpha-beta)+cos(alpha+beta)Big))
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
(sinalphasinbeta=dfrac12Big(cos(alpha-beta)-cos(alpha+beta)Big))
3) Сложим формулы синуса суммы и синуса разности двух углов:
(sin(alpha+beta)=sinalphacosbeta+sinbetacosalpha)
(sin(alpha-beta)=sinalphacosbeta-sinbetacosalpha)
Получим: (sinalphacosbeta=dfrac12Big(sin(alpha-beta)+sin(alpha+beta)Big))
(blacktriangleright) Вывод формул суммы/разности функций:
Обозначим (alpha+beta=x, alpha-beta=y). Тогда: (alpha=dfrac{x+y}2, beta=dfrac{x-y}2). Подставим эти значения в предыдущие три формулы:
1) (2cos{dfrac{x+y}2}cos{dfrac{x-y}2}=cos x+cos y)
Получили формулу суммы косинусов.
2) (2sin {dfrac{x+y}2}sin {dfrac{x-y}2}=cos y-cos x)
Получили формулу разности косинусов.
3) (2sin {dfrac{x+y}2}cos {dfrac{x-y}2}=sin y+sin x)
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
(sin x-sin y=sin x+sin(-y)=2sin {dfrac{x-y}2}cos
{dfrac{x+y}2})
5) (mathrm{tg},alphapmmathrm{tg},beta=dfrac{sinalpha}{cosalpha}pmdfrac{sinbeta}{cosbeta}=dfrac{sinalphacosbetapmsinbetacosalpha}{cosalphacosbeta}=dfrac{sin(alphapmbeta)}{cosalphacosbeta})
Аналогично выводится формула суммы котангенсов.
(blacktriangleright) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
1) (sin2alpha=dfrac{sin2alpha}1=dfrac{2sinalphacosalpha}{sin^2alpha+cos^2alpha}=)
(разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0) и (sin2alpha=0)):)
(=dfrac{2mathrm{tg},alpha}{1+mathrm{tg}^2,alpha})
2) Так же, только делением на (sin^2alpha), выводится формула для косинуса.
(blacktriangleright) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
Рассмотрим выражение (asin x+bcos x). Домножим и разделим это выражение на (sqrt{a^2+b^2},):
(asin x+bcos x=sqrt{a^2+b^2}left(dfrac a{sqrt{a^2+b^2}}sin x+
dfrac b{sqrt{a^2+b^2}}cos x right)=sqrt{a^2+b^2}big(a_1sin x+b_1cos xbig))
Заметим, что таким образом мы добились того, что (a_1^2+b_1^2=1),
т.к. (left(dfrac a{sqrt{a^2+b^2}}right)^2+left(dfrac
b{sqrt{a^2+b^2}}right)^2=dfrac{a^2+b^2}{a^2+b^2}=1)
Таким образом, можно утверждать, что существует такой угол (phi), для которого, например, (cos phi=a_1, sin phi=b_1). Тогда наше выражение примет вид:
(sqrt{a^2+b^2},big(cos phi sin x+sin phicos
xbig)=sqrt{a^2+b^2},sin (x+phi)) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: [{large{asin x+bcos x=sqrt{a^2+b^2},sin (x+phi),}} quad text{где } cos phi=dfrac
a{sqrt{a^2+b^2}}] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt{a^2+b^2},cos (x-phi)]
(blacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла:
(a) sin xpmcos x=sqrt2,left(dfrac1{sqrt2}sin
xpmdfrac1{sqrt2}cos xright)=sqrt2, sin
left(xpmdfrac{pi}4right))
(b) sqrt3sin xpmcos x=2left(dfrac{sqrt3}2sin xpm
dfrac12cos xright)=2, sin left(xpmdfrac{pi}6right))
(c) sin xpmsqrt3cos x=2left(dfrac12sin
xpmdfrac{sqrt3}2cos
xright)=2,sinleft(xpmdfrac{pi}3right))