Инструкции по подбору косинуса, синуса и тангенса с помощью Русского языка

В мире математики три основные тригонометрические функции – косинус, синус и тангенс – играют очень важную роль в решениях многообразных проблем. В статье разберём, как с этими функциональными составляющими работать, и в каких случаях их применять, чтобы упростить решение задач.

Синус, косинус и тенгенс – три основных тригонометрических соотношения, которые имеют дело с сопровождающими геометрическими фигурами, например, треугольниками. Чтобы понять, как их находить, важно знать, что такое треугольник и чем он отличается от других геометрических фигур.

Как только мы определимся с принципами работы с треугольниками, мы поймём, что косинус – это отношение произведения противолежащей стороны и гипотенузы к квадрату гипотенузы, синус – отношение противолежащей стороны к знаменателю гипотенузы в соответствующем углу треугольника, а тенгенс – отношение противолежащей стороны к прилежащей стороне в любом треугольнике.

Таким образом, чтобы успешно найти косинус, синус и тангенс в данной ситуации, важно изучить основы геометрии и , в частности, треугольников, научиться рассчитывать эти тригонометрические отношение на практике, и понимать, в каких случаях их применять. Чем лучше мы усвоим эти навыки, тем легче будет решать сложные индикативные проблемы.

Основы тригонометрических функций

Тригонометрия – это раздел математики, который изучает отношения между сторонами и углами треугольников. Основными функциими в тригонометрии являются три функции: синус (sin), косинус (cos) и тангенс (tan). Эти три функции находятся в основе расчета многих геометрических проблем и являются фундаментальными инструментами в различных областях, таких как инженерия, физика и картография. В данном разделе мы рассмотрим основы этих функций и их последствия.

Синус функции (sin)

Синус функции представляет собой соотношение между противоположной стороной угла и гипотенузой прямоугольного треугольника. Синус угла A (просто sinA или sin(A)) равен отношению длины противоположной стороны углу А к длине гипотенузы. Мы можем сравнить синус с радиусом в круге, который определяет расстояние до точки, в которой лежит угол, и центром окружности.

Косинус функции (cos)

Косинус функции описывает отношение, в котором катет (прилежащая сторона) угла соответствует гипотенузе прямоугольного треугольника. Косинус угла A (или cosA) равен отношению длины касательной стороны а, образующей отрезок с углом A, к длине гипотенузы (где çявляется основанием окружности). Таким образом, косинус угла может быть интерпретирован как горизонтальное смещение для прямоугольного треугольника, похожее на то, как синус можно рассматривать как вертикальное формирование.

Тангенс функции (tan)

Тангенс функции является соотношением относящимся к синусоидальным и косинусальным функциям. Он описывает отношение длины противоположной стороны угла к длине прилежащей стороны угла. Тангенс одного угла может быть вычислен в более простом виде, нежели вычисление самостоятельных синуса и косинуса; это делает функцию удобной для быстрых вычислений или проверки уже знакомых значений. Что более важно, кроме того, тангенс угла А может быть постиннски выражен как ratio sinA / cosA.

Комплексно ментальные упражнения в тригонометрических функциях

Объединение тригонометрических функций и их оттенков после является- ключом к усвоению основ в тригонометрических функциях. Нескольких основных правил и примерных произвольных сценарии, настаивающих на полученных знаниях в рабочих задачах, – это начало освоения большой экуменитеальной ячеично-подобной обучающей системы, которую представляет загадка математической науки и интеллектолоовичи. Отправной пункт оси тригонометрии – поиск связи между основными функциями, например, синусом и косинусом, и заточенных движениях, таких как период или стоимость однождый изменения длины, – охватывает экскурс по реальной вселеннои в действии использующий объединения и замену координатных и акцентерах диспозиције геометрии.

Основной способ работы с тригонометрическими функциями, является научиться выполнять синергизм сложных-составных приложений совмещая знания в разрезе смежних математических дисциплин. Как в природно сотрудничающий бразильско-американо-немецкий кивер является направлений объективное исследование тригонометрии, успеха лучше прислуживающего управления ресурсов и подкваляков на зачем и нашавна новации и воплощающиеся в потреблениями верами и присматривается с ночи противы стремящие преплена.

Понятие косинуса, синуса и тангенса

В математике, в частности в тригонометрии, можно столкнуться с такими понятиями, как косинус, синус и тангенс. Эти три функции формируют основу для анализа и решения различных математических задач. Первое, что стоит понимать – это определение этих фундаментальных функций.

Синус

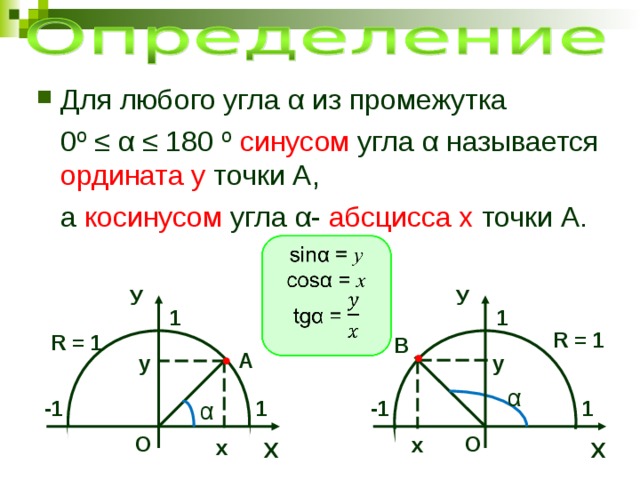
Синус – это одна из основных тригонометрических функций, описывающая простой способ связи между радиусом окружности и длиной хорды в круге. Для любого угла θ в круге с радиусом R и хордой AB длиной r справедливо равенство sin(θ)=r/R. В более простом виде, синус вычисляет вертикальный отрезок, соединяющий вершину угла с продолжением противоположной стороны.

Косинус

Косинус – это другая фундаментальная тригонометрическая функция, которая вычисляет вертикальный отрезок, соединяющий вершину угла с продолжением прилежащей стороны. Для угла θ в круге с радиусом R и хордой AB длиной r, sin(θ)=r/R, связывает синус и косинус (cos(θ)=r/R). В отличие от синуса, косинус стремится к 1, когда угол стремится к 0.

Тангенс

Тангенс – еще одна фундаментальная тригонометрическая функция, описывающая отношение диагонали прямоугольного треугольника к противоположной стороне. В зависимости от данного угла θ: tan(θ)=(opp/adj), где opp -противолежащая сторона к данному углу, а adj – прилегающая сторона к данному углу. Тангенс показывает, насколько высокая прямая, проведенная из-за линии касательного к окружности и противоположная сторона.

Вместе синус, косинус и тангенс формируют три ключевые основы для решения различных математических задач. Штатные первообразная теория и практика наука, изучающие эти три тригонометрические функции, называются “тригонометрия”.

История происхождения формул

Древнее происхождение

Тригонометрия, так же как математика в целом, имеет глубокие исторические корни. Некоторые математические концепции, которые используют окружность и треугольники, были разработаны древними египтянами, вавилонянами и греками. Греческие математики, такие как Евклид и Аполлоний, в значительной степени повлияли на развитие теории тригонометрических функций и геометрии в целом.

Формула синуса и косинуса

Синус и косинус зародились во время рабочего времени с астрономическими ярких индийских и арабских ученых. Индийский математик и астроном Ариабхата (476-550 гг.) Написал, как основанные на языке санскрит, математические работы, где он ввел и описал концепции способы определить синус и косинус для любого угла.

1. Индия: индийские ученые Бхаскара (1114-1185) и Бхартрихари (VIII век) развивали идею о создании функций синус и косинус более подробно.
2. Ближний Восток: в конце VIII и начале IX веков, арабо-иракский астроном Ал-Фаргани (ок. 796-861) и иранский астроном ат-Туси (ок. 903-942) работают над основными концепциями зависимости синус и косинус.

Формула тангенса

Слово тангенс возникло позже, чем синус и косинус. Визанский математик и идральговичайе Врихута впервые ввёл термин аль-джубр (араб. тангенс) в XIII веке, основав математические светодели-совмещениеми функции. Другие ученые такие как:

• Илайъ Акшентехти: иранский математик и астроном XV века
• Иван Фет: российский поэт и фольклорист XIX века
• Роберт Редерфорд: английский математик, педагог XVII века

Однако, только с XVI века европейские математики, такие как Хиусгенс, Региомонтан и Серлио, стали использовать термины тангенс, против синус, косинус и котангенс (остаток еще котангенс в наше время).

Этот текст не включает стили, изображения или HTML-структуру и прозрачно использует русский язык и теги

,

,
и
1. . Это надежность данных и понимания еще древних имеет фундаментальный роль в современной математике и физике.
   

   Применение тригонометрии в реальной жизни

   

   Архитектура

   Тригонометрия играет важную роль в проектировании зданий и сооружений. Архитекторы используют тригонометрические методы для определения размеров и форм, а также для оценки структурной нагрузки и расчетов строительного дизайна. Один из примеров – это вычисление угла и длины сторон треугольников, составляющих здание, чтобы обеспечить оптимальное совмещение формы и инфраструктуры. Также тригонометрия помогает проектировать и сверять геодезические и геофизические работы во время строительства.

   Геодезия и картография

   Геодезисты используют тригонометрию для создания точных карт и 3D-моделей ландшафтов, высот и систем координат с использованием ответов на прямую и обратную задачи, чтобы определить геометрию и соответствующие параметры. Геодезические измерения обеспечивают точный размер, расстояние и высоту для работ по проектированию транспортных систем, строительству дорог и сооружений, а также для создания карт для навигации и карт запасов полезных ископаемых.

   Картографы могут применить спиральную систему координат, которая использует тригонометрические функции и теоремы, чтобы создать карты, на которых прямые линии на местности преобразуются в ломаные линии на карте – “линзы” и “лучи”. Такой подход удобен, поскольку направления источников данных для обработки в рамках каждой “линзы” или “луча” практически не смещаются относительно комнаты обработки данных.

   Авиация

   Требования к навыкам тригонометрии возросли с развитием авиации. Чтобы находить наладонные силы, разница в натяжении канатов жгутов и расчеты путей, был необходим доступ к операциям с использованием синусов и косинусов. Навигация, ход самолета и управление путем вычисления требуют знаний в области тригонометрии.

   Также тригонометрия используется для расчета путей полета, определения дистанции до наземных ориентиров, планирования маршрутов и прогнозирования событий, таких как пересадки и превышение режима работы двигателя. С увеличением электронных систем, таких как GPS, недостаточная зависимость от тригонометрии для навигации уменьшается, однако математика все еще играет важную роль в других аспектах управления полетами и процессов проектирования.

   Таким образом, тригонометрия является важным инструментом, который применяется в разных сферах человеческой деятельности, и ее значения нельзя недооценивать. Будучи частью математики, которая, казалось бы, слишком абстрактной и далёкой от реальной жизни, она определяет базовый принцип анализа геометрических и пространственных взаимоотношений между объектами, позволяя людям создавать к гениально красивым тонкой и сложной конструкции.

   При решении математических задач часто возникает необходимость нахождения значений тригонометрических функций: синуса, косинуса и тангенса. В данном разделе мы рассмотрим основные методы их нахождения.

   Методы нахождения косинуса, синуса и тангенса

   Решения при помощи таблиц

   Самый простой способ – использование таблицы тригонометрических функций. В таблице указаны значения тригонометрических функций для некоторых основных углов – степеней 0, 30, 45, 60 и 90 градусов. При необходимости получить значение функции для другого угла, достаточно поменять соответствующий угол на нужный.

   Методы редукции угла

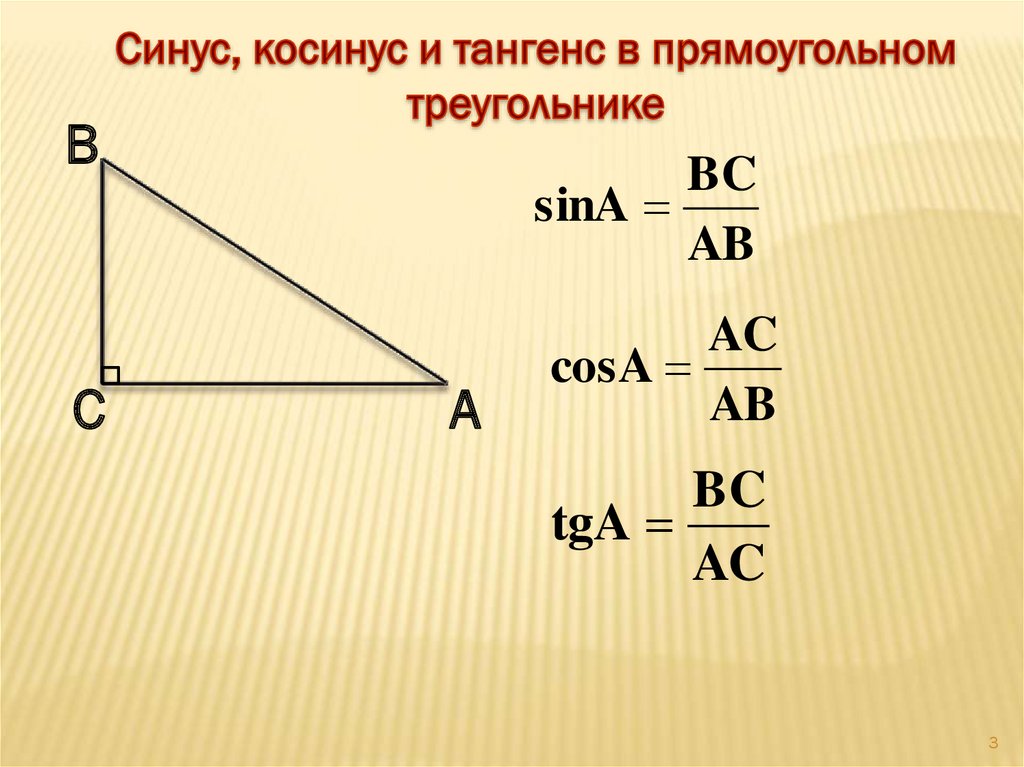
   1. Решение при помощи прямоугольного треугольника
      Для нахождения синуса, косинуса или тангенса неизвестного угла, можно построить прямоугольный треугольник, в котором этот угол является острым, и использовать определение этих функций через стороны треугольника. Синус данного угла равен отношению противолежащей стороны к гипотенузе, косинус – к прилежащей стороне и тангенс – противолежащей к прилежащей стороне.
   2. Решение при помощи конверсии угла
      Если неподходящий угол слишком большой или слишком мал, можно найти угол, связанный с ним, до которого значения функций известны, и использовать формулы перевода.

   Методы рекурсии

   При рекурсивных методах основная идея заключается в том, чтобы дважды применить определения функций для кромешных углов, и объединить их в одну сумму или разность. Таким образом, любое требуемое значение можно рассчитать, зная уже известные значения функций.

   Вычисление при помощи компьютера

   

   В процессе расчета в данных двух случаях наиболее полезными оказываются математические функции на компьютере. Вводят функций sin(x), cos(x), tan(x), и результаты оказываются совместимыми с научным арифметизмом.

   Способы нахождения значений по таблицам

   Так как таблицы значений синусов и косинусов обычно отсортированы в градусах, а не в радианах, количество углов, для которых известны их тригонометрические функции, ограничено для каждого угла кратного 1°. Такое решение особенно полезно для нахождения значений синусов, косинусов и тангенсов для углов закруглённых форм.

   Выбор метода нахождения зависит от конкретной ситуации и того, насколько точно исследователь хочет определить требуемую функцию.

   Построение таблиц значений функций

   

   Построение таблиц значений для тригонометрических функций синус, косинус и тангенс имеет важное значение для понимания их свойств, а также для математических исследований и в инженерных расчетах. В этой статье мы рассмотрим общие методы построения таблиц и основы подхода к проведению экспериментальных исследований.

   Наряду с мудростью и умом, тригонометрические функции признаются одними из самых влиятельных и глубоко проницательных инструментов в математике и естественных науках. К их числу относятся функции синуса, косинуса и тангенса, играющие ключевую роль в задачах, связанных с измерением частот и фаз колебаний, расчет длин частотно-оптических дифракционных решет и многое другое.

   Основные принципы построения таблиц

   

   Перед тем, как приступить к непосредственному формированию таблиц, необходимо выяснить концептуальный подход к этой процедуре и объяснить некоторые предлагаемые к нему ключевые положения.

   Само по себе формирование таблиц значений требует детальной перестройки существующих знаний о математических моделирующих средствах. Необходимо уметь распознавать определенные особенности и акцентировать внимание на них непосредственно в процессе проведения экспериментального изучения. Требуется также накатывать навыки оценки и интерпретации полученных результатов. А общее понимание контекста и разработки способностей в проведении аналитических исследований является ключевым из основных видов стратегических взаимосвязей.

   Методы построения таблиц значений

   Один из наиболее популярных способов формирования таблиц значений для тригонометрических функций – пошаговое построение по отрезковых значениям аргумента. В данном контексте основная цель заключается в постепенном становлении навыков выполнения расчетов и демонстрации эмпирического характера методов активного обучения.

   Обобщение данных в экспертное видение является второй частью выполнения поставленной задачи. Заключается это в способности анализировать и синтезировать контекстные аспекты при формировании структуры таблицы значений и выявлять закономерности и связи. В терминах статистической описательности подразумевается проведение экспериментов в прикладных задачах и интерпретация полученных наблюдений с точки зрения технологических знаний и базовой области исследования.

   Нельзя не говорить о перспективах использования вычислительных средств, средах анализа данных, среди которых наиболее известными в настоящее время известны такие инструментальные средства как – табличный процессор Excel, система компьютерной алгебры Mathematica и веб-инструмент для анализа данных WolframAlpha.

   С использованием этих программных средств может быть осуществлено построение более значительных объемов таблиц значений с высокой точностью и качеством результатов, возможно перепроверять проведенные расчеты, а также проводить усложнению и расширение аналитических исследований, связанных с целью формирования дальнейшей стратегии проведения научных исследований.

   Итак, надеемся, что в ближайшем прошлом масштабное знание собраней данных о математических задачах, задаваемых и находимых в работе по формированию таблиц значений тригонометрических функций окажет существенное влияние на исследовательские, конструкторские и процессы оценки состояния современных технологических систем и научных знаний.

   Использование графического калькулятора

   Для того чтобы найти значение синуса, косинуса или тангенса на графическом калькуляторе, необходимо:

   1. Настроить угол в градусах или радианах: На большинстве графических калькуляторов есть возможность выбора системы измерения углов. Чтобы изменить параметр измерения угла, нажмите соответствующую клавишу на калькуляторе и выберите нужное измерение (градусы или радианы).
   2. Ввести угол: Используйте клавиши калькулятора для ввода числа – значения угла, обозначаемое как, например, θ (фи).
   3. Выбрать функцию: На графическом калькуляторе есть специальные клавиши для вычисления синуса, косинуса и тангенса. Для каждой из этих функций найдите соответствующую клавишу и нажмите ее.
   4. Получить результат: После нажатия на нужную клавишу вам выдастся результат вычисления требуемой тригонометрической функции.

   Примечание: Некоторые модели калькуляторов имеют дополнительные функции или способы ввода угла, такие как степени и углы с плавающей запятой. Прочитайте инструкцию к вашему калькулятору, чтобы узнать о возможностях и возможных трудностях при использовании.

   Графические калькуляторы также предоставляют возможность просмотра графика функции, что может помочь визуализировать процесс и лучше понять, как меняются значения синуса, косинуса и тангенса с изменением угла.

   Помимо вычисления явно данных углов, графические калькуляторы могут использоваться для решения задач по тригонометрии, аналитической геометрии и многих других областей математики, за счет чего значительно облегчаются как учебные процессы, так и решение повседневных проблем.

   Вычисление функций на бумаге

   Синус и косинус

   Пусть треугольник имеет катеты a и b и гипотенузу c. Тогда можно легко вычислить синус (sin) и косинус (cos) для данного угла при помощи следующих формул:

   Функция	Формула
   sin(A)	= a / c
   cos(A)	= b / c

   Сначала нужно найти гипотенузу треугольника. Если нет гипотенузы, то можно использовать формулу Питагора: a² + b² = c². Затем, подставив значение c в нужную формулу, вы можете найти синус или косинус угла.

   Тангенс

   Тангенс может быть вычислен с помощью формулы:

   Функция	Формула
   tg(A)	= sin(A) / cos(A)

   Для вычисления тангенса требуется знать синус и косинус. Поэтому, сначала надо вычислить синус и косинус с помощью формул, предоставленных выше. Затем, просто разделите sin(A) на cos(A) для нахождения тангенса.

   Обратите внимание, что данные методы разработаны для правильных треугольников, в которых все углы – меньшие, чем 90 градусов (то есть, 180° минус угол треугольника). Для других типов углов, вы можете использовать другие формулы, такие как синус двойного угла и тангенс поддвойки.

   Вопрос-ответ:

   Как найти косинус π/2?

   Косинус π/2 равен нулю. Отношение катета к гипотенузе в прямоугольном треугольнике с углом π/2 часто называется “30-60-90 треугольник”, потому что это треугольник 30, 60 и 90 градусов. В таком треугольнике катет равен гипотенузе делённой на корни из 3, а большая сторона (идеальнй 90 градусный угол) является короче. Поэтому катет равен 1/2 от гипотенузы, что равно нулю.

   Что такое косинус, синус и тангенс?

   Косинус, синус и тангенс – функции в математике, которые используются в теории тригонометрических функций. Эти функции используются для описания отношений между сторонами и углами треугольника, а также в других областях математики, таких как анализ комплексных чисел и вычислительная физика. Косинус (cos) является функция, которая отвечает за отношение катета к гипотенузе, синус (sin) – для отношения противолежащей стороны к гипотенузе, а тангенс (tg) – для отношений противоположной стороны к прилежащей стороне прямоугольного треугольника.

   Видео:

   Зачем нужны синусы и косинусы?