В статье рассматриваются определения угла между скрещивающимися прямыми с приведением графических иллюстраций. При имеющихся координатах направляющих векторов заданных прямых научимся находить искомый угол. В заключительной части решим задачи на нахождение угла.
Угол между скрещивающимися прямыми – определение
Для нахождения искомого угла необходимо пройти несколько этапов.
Две прямые в трехмерном пространстве называются скрещивающимися в случае, если они не находятся в одной плоскости.
Из определения о скрещивающихся прямых следует, что они не являются параллельными или пересекающимися и не совпадают, тогда они находились бы в одной и той же плоскости.
Рассмотрим рисунок, приведенный ниже.

В трехмерном пространстве имеются скрещивающиеся прямые a и b. Проведем прямые а1 и b1 параллельные скрещивающимся a и b. Точка М1 является точкой пространства, через которую они проходят. Отсюда получаем, что а1 и b1 являются пересекающимися прямыми.
Обозначим угол между a1 и b1 равным значению α. Построение прямых a2 и b2 параллельно скрещивающимися относительно a и b в точке М2 отличной от М1 приводит к тому, что значение угла между ними обозначим как α. То есть угол между прямыми a1 и b1 равен углу между a2 и b2. В этом можно убедиться, если про/извести параллельный перенос. Тогда точки М1 и М2 совпадают.
Углом между скрещивающимися прямыми называют угол, который образуется между двумя параллельными заданными скрещивающимися прямыми.
Отсюда следует, что угол не зависит от точки M и ее выбора. Поэтому точка M может быть любой. Рассмотрим рисунок, приведенный ниже.

Нахождение угла между скрещивающимися прямыми
Угол между скрещивающимися прямыми определяется через угол пересекающихся прямых. Поиск угла сводится к его нахождению между пересекающимися прямыми пространства. Школьные методы решения основываются на необходимости построения на основе подобия фигур или теоремах косинуса, что позволит определить синус, косинус, тангенс угла прямоугольного треугольника.
Удобным способом решения считается нахождение угла методом координат. Рассмотрим его.
Трехмерное пространство имеет прямоугольную систему координат Охуz. Имеется задача, в которой необходимой найти угол α, образованный скрещивающимися прямыми a и b с заданными уравнениями прямых в пространстве.
Для решения необходимо взять произвольную точку в трехмерном пространстве и обозначить буквой M, что дает понять, через нее проходят прямые a1 и b1, которые параллельны скрещивающимся a и b. Угол α , образованными прямыми a и b, из этого определения получится равным пересекающимся a1 и b1.
Для нахождения искомого угла между a1 и b1 необходимо использовать формулу для нахождения угла между пересекающимися прямыми, а для этого нужно знать значение координат направляющих векторов у прямых a1 и b1.
Для их получения необходимо применить определение направляющего вектора, которое говорит о том, что множества векторов совпадают. Направляющие векторы прямых обозначают a→=(ax, ay, az) и b→=(bx, by, bz).
Векторы a→ и b→ имеют координаты, определяющиеся из условия по уравнению или по координатам точек пересекающихся прямых. Тогда получаем, что угол между двумя скрещивающимися прямыми a и b вычисляется из формулы α=arccosa→, b→a→·b→=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2, а a→=(ax, ay, az) и b→=(bx, by, bz) являются направляющими векторами прямых a и b.
Использование формулы для нахождения косинуса угла между скрещивающимися прямыми а и b дает выражение вида cos α=a→, b→a→·b→=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2.
При помощи основного тригонометрического тождества можно найти синус угла между этими прямыми при известном косинусе из формулы sin α=1-cos2 α.
Найти угол между скрещивающимися прямыми a и b, которые заданы уравнениями x2=y-40=z+1-3 и x=1+λy=1-λz=-3+4·λ, λ∈R и определяются в системе координат Охуz.
Решение
Для определения координат необходимо использовать каноническое уравнение прямой в плоскости. необходимо обратить внимание на знаменатель дробей. Отсюда видно, что a→=(2, 0, -3) является направляющим вектором прямой x2=y-40=z+1-3. При наличии параметрического уравнения можно определить координаты направляющего вектора, так как она равняются коэффициентам, тогда получаем, что b→=(1, -1, 4) является направляющим вектором для прямой вида x=1+λy=1-λz=-3+4·λ, λ∈R.
Отсюда получаем, что имеются все необходимые формулы и данные для того, чтобы произвести вычисление угла между скрещивающимися прямыми. Имеем, что
α=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2=arccos2·1+0·(-1)+(-3)·422+02+(-3)2·12+(-1)2+42==arccos1013·18=arccos10326
Ответ: угол между скрещивающимися прямыми равен arccos10326.
Найти значение синуса и косинуса угла между скрещивающимися прямыми, где имеются ребра AD и ВС, принадлежащие пирамиде ABCD, с известными вершинами с координатами A(0, 0, -1), B(5, 7, -5), C(3, 7, -5), D(1, 3, 1).
Решение
AD→ и BC→ являются векторами соответствующих сторон заданной фигуры. Необходимо вычислить координаты с помощью имеющихся данных начала и конца.
Получаем, что AD→=(1-0, 3-0, 1-(-1))⇔AD→=(1, 3, 2)BC→=(3-5, 7-7, -5-(-3))⇔BC→=(-2, 0, -2)
Из формулы cos α=arccosAD→, BC→AD→·BC→ находим косинус угла между заданными скрещивающимися прямыми. Получаем выражение вида
cos α=1·(-2)+3·0+2·(-2)12+32+22·(-2)2+02+(-2)2=614·8=327
Перейдем к вычислению синуса угла между этими прямыми. Подставляем значения и получаем, что sin α=1-cos2α=1-3272=1927.
Ответ: sin α=1927, cos α=327.
В заключительном этапе рассмотрим задачу, в которой нужно найти угол между скрещивающимися прямыми с самостоятельно введенной системой координат.
Имеется прямоугольный параллелепипед ABCDA1B1C1D1 со сторонами АВ=3, АD=2 и AA1=7 единиц. Точка E делит прямую АА1 как 5:2. Определить угол между скрещивающимися прямыми ВЕ и А1С.
Решение
Ребра заданного параллелепипеда являются взаимно перпендикулярными, поэтому необходимо ввести прямоугольную систему координат для определения угла между указанными скрещивающимися прямыми с помощью метода координат.
Для начала вводится прямоугольная система координат Охуz. Получаем, что начало координат является совпадающим с вершиной A, а Ох совпадает с прямой AD, Оу с AB, а Оz с АА1. Рассмотрим рисунок, приведенный ниже.

Отсюда имеем, что точка B с координатами (0, 3, 0), E – (0, 0, 5), AА – (0, 0, 7), C – (2, 3, 0). Исходя из координат, мы можем получить координаты векторов BE→ и A1C→, необходимые для дальнейшего решения задачи. Получаем, что BE→=(0, -3, 5), A1C→=(2, 3,-7).
Применим формулу для нахождения угла, образованного скрещивающимися прямыми, при помощи координат направляющих векторов. Получаем выражение вида
α=arccosBE→, A1C→BE→·A1C→=arccos0·2+(-3)·3+5·(-7)02+(-3)2+52·22+32+(-7)2==arccos4434·62=arccos22527
Ответ: arccos22527.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
25
Апр 2012
13 Задание (2022) (C2)
 В этой статье я расскажу, как находить угол между скрещивающимися прямыми с помощью метода координат.
В этой статье я расскажу, как находить угол между скрещивающимися прямыми с помощью метода координат.
Если мы решили использовать этот метод, то будем придерживаться такого алгоритма:
1. Вводим систему координат.
2. Находим координаты направляющих векторов данных прямых.
3. По формуле косинуса угла между векторами находим косинус угла между направляющими векторами.
Косинус угла между векторами 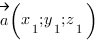 и
и 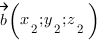 вычисляется по формуле:
вычисляется по формуле:
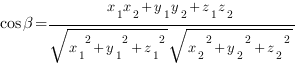
Вот, собствено, и все.
Важное уточнение: за угол между прямыми принимают меньший из двух углов, образованный этими прямыми, поэтому косинус угла между прямыми должен быть больше нуля, и он равен модулю косинуса угла между направляющими векторами.
Решим задачу.
В правильной шестиугольной призме 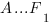 , все ребра которой равны 1, найти косинус угла между прямыми
, все ребра которой равны 1, найти косинус угла между прямыми 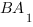 и
и 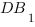 :
: 1. Введем систему координат:
1. Введем систему координат:
 2. а) Найдем координаты направляющего вектора прямой
2. а) Найдем координаты направляющего вектора прямой  , для этого найдем координаты точек
, для этого найдем координаты точек 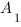 и
и 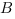 .
.
Длину отрезка  найдем по тереме косинусов из треугольника
найдем по тереме косинусов из треугольника  :
:


 ;
; 
Чтобы найти координаты вектора  , из координат конца вычтем координаты начала. Получим:
, из координат конца вычтем координаты начала. Получим: 
б) Найдем координаты направляющего вектора прямой  , для этого найдем координаты точек
, для этого найдем координаты точек  и
и 



3. Найдем косинус угла  между векторами
между векторами  и
и  .
.


Ответ: 

И.В. Фельдман, репетитор по математике.

|
Отзывов (9)
| Метки: решение задания С2
Учебник
Геометрия, 10 класс
Угол между скрещивающимися прямыми в пространстве
Скрещивающиеся прямые – не параллельны, не имеют общих точек, не пересекаются.
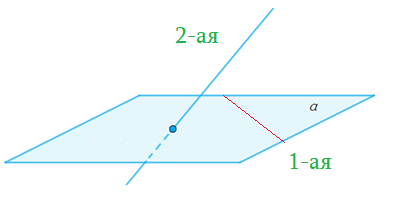
Признаки Скрещивающихся прямых
- 1-ая прямая лежит в плоскости, а 2-ая пересекает плоскость в точке не из 1-ой, то прямые скрещивающиеся.
- Через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой. Единственная.
- Скрещивающиеся $a$ и $b$ : есть пара пареллельных плоскостей $alpha$ и $beta$, таких что $ain alpha$, $bin beta$
Задача 1: В прямоугольном параллелепипеде $ABCDMNKL$ найти угол между
скрещивающимися прямыми $AN$ и $BK$, если известны ребра $BA=36$, $BN=15$, $BC=20$
- Как находить угол между двумя стереометрическими объектами? по алгоритму параллельных переносов, совмещений.
- Свойство инвариантности углов при параллельном переносе стереометрических объектов – прямых, плоскостей:
- Если объекты $A$ и $B$ параллельны соответственно $A’$ и $B’$, то углы между парами равные: $angle left(A;Bright)=angle left(A’;B’right)$
- В нашем случае, $BKparallel AL$, поэтому равны углы $angle left(AN;BKright)=angle left(AN;ALright)=angle NAL$
- Перетащим $BK$ по плоскости $BKLA$ вдоль $BA$ до совмещения с точкой $A$. Тогда $BK$ совметится с отрезком $AL$.
- Итак, мы ищем угол $angle NAL$. Найдем его через теорему косинусов в треугольнике $ANL$ для угла $angle NAL$ :
- *** $NL^2=AN^2+AL^2-2cdot ANcdot NLcdot cos angle NAL$
- Стороны $AN$, $NL$ и $AL$ можем признать диагоналями граней – прямоугольников, значит, найти их по теоремам Пифагора.
- Решение: $AN=sqrt{36^2+15^2}=39$ $AL=sqrt{20^2+15^2}=25$ $NL=sqrt{36^2+20^2}=4cdot sqrt{106}$
- Из теоремы косинусов $cos angle NAL=frac{AN^2+AL^2-NL^2}{2cdot ANcdot AL}=frac{39^2+25^2-16cdot 106}{2cdot 39cdot 25}=frac{450}{1950}=frac{3}{13}$ Ответ: $angle NAL=arccos frac{3}{13}$
- Признак: $NAL$ – плоскость угла: $ANin NAL$ и $BKparallel NAL$
case I 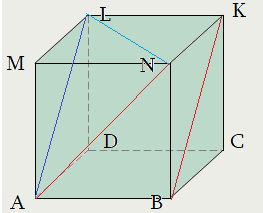 case II
case II 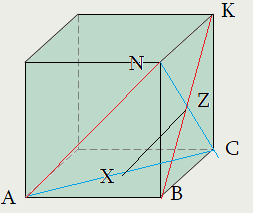
Алгоритм: нахождение угла между прямыми путем параллельного переноса (демонстрация по II, прямые $AN$, $BK$ ):
1-ый шаг: Выбираем точку, в которой хотим совместить прямые. Например, точку $Z$ – середину отрезка $BK$.
2-ой шаг: Для прямой $AN$ определим плоскость “скольжения” – плоскость, содержащая эту прямую и точку $Z$. Это $ANC$
3-ий шаг: Двинем прямую $AN$ по плоскости $ANC$ оставаясь параллельно “как стержень”. Она совместится с отрезком $ZX$.
4-ый шаг: Что за точка $X$ ? угол $angle XZB$ – именно то, что нам нужно: $angle XZB=angle left(XZ;BKright)=angle left(AN;BKright)$.
Признак: – увидеть ту главную плоскость угла , которая параллельна обеим скрещивающимся прямым. Здесь это $XZB$.
Задача 2: В правильной треугольной призме все ребра 1. Найти косинус угла $angle left(AB;CMright)$
- $ABCMNK$ правильная призма: в основании правильный $bigtriangleup ABC$ , ребро $BN$ перпендикулярно основанию.
- Нужен угол между $AB$ и $CM$. Выберем Точкой совмещения $M$. Прямая $CM$ уже проходит через нее.
- Прямая $AB$ и точка $M$ лежат в плоскости $ABNM$. Значит, $ABNM$ – плоскость сколжения. $AB$ перейдет в $MN$.
- Путем параллельного совмещения $AB$ с $MN$ мы устоновили, что искомый угол – это $angle CMN$.
- Косинус угла $angle CMN$ можно найти по теореме косинусов треугольника $CMN$: $cos angle CMN=frac{CM^2+MN^2-CN^2}{2cdot CMcdot MN}$
- Признак: $CMN$ – плоскость угла: $ABparallel CMN$ и $MCin CMN$
k задачe 2 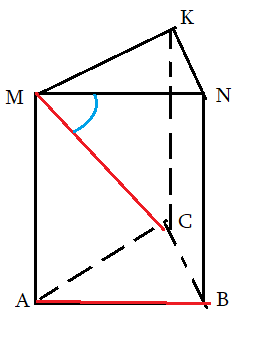 к задаче 3
к задаче 3 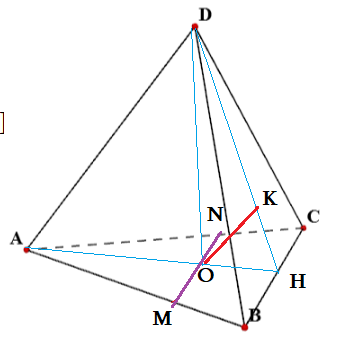
Задача 3: В правильном тетраэдре $DABC$ все ребра 1 см. Найти угол между $AD$ и $BC$.
- Для нахождения угла, совместим “движениями” наши прямые в точку $O$ – основание высоты $DO$ .
- В правильном тетраэдре в основании равносторонный треугольник $DABC$, высота пирамиды попадает в центр окружностей.
- Точка $O$ – пересечение высот, медиан, биссектрис. $O$ лежит на высоте $AH$ , $DH$ – высота грани $BDC$.
- В точке $O$ проведем прямую параллельную прямой $BC$. Им будет линия $MN$
- В точке $O$ проведем прямую $OK$, параллельную $AD$. Она будет лежат в плоскости $ADH$ Значит, $Kin DH$.
- Итак, “взамен” наших $AD$ и $BC$ мы получили прямые $OK$ и $MN$ : $OKparallel AD$, $MNparallel BC$
- по свойству углов при параллельном переносе $angle left(AD;BCright)=angle left(OK;MNright)=angle MOK$
- Найти $angle MOK$ ? Легко! учтите, что у нас правильный тетраэдр и находите.
- Признак: $MONK$ – плоскость угла: $ADparallel MONK$ и $BCparallel MONK$
Алгоритм: вычисление угла в пространстве или плоскости
- В каком треугольнике этот угол? узнать стороны треугольника и найти угол по теореме косинусов.
- Если треугольник окажется равнобедренным, то провести высоту и найти угол прямоугольного треугольника.
- А если треугольник прямоугольный, то написать cos или sin или tg этого угла и найти как arc !
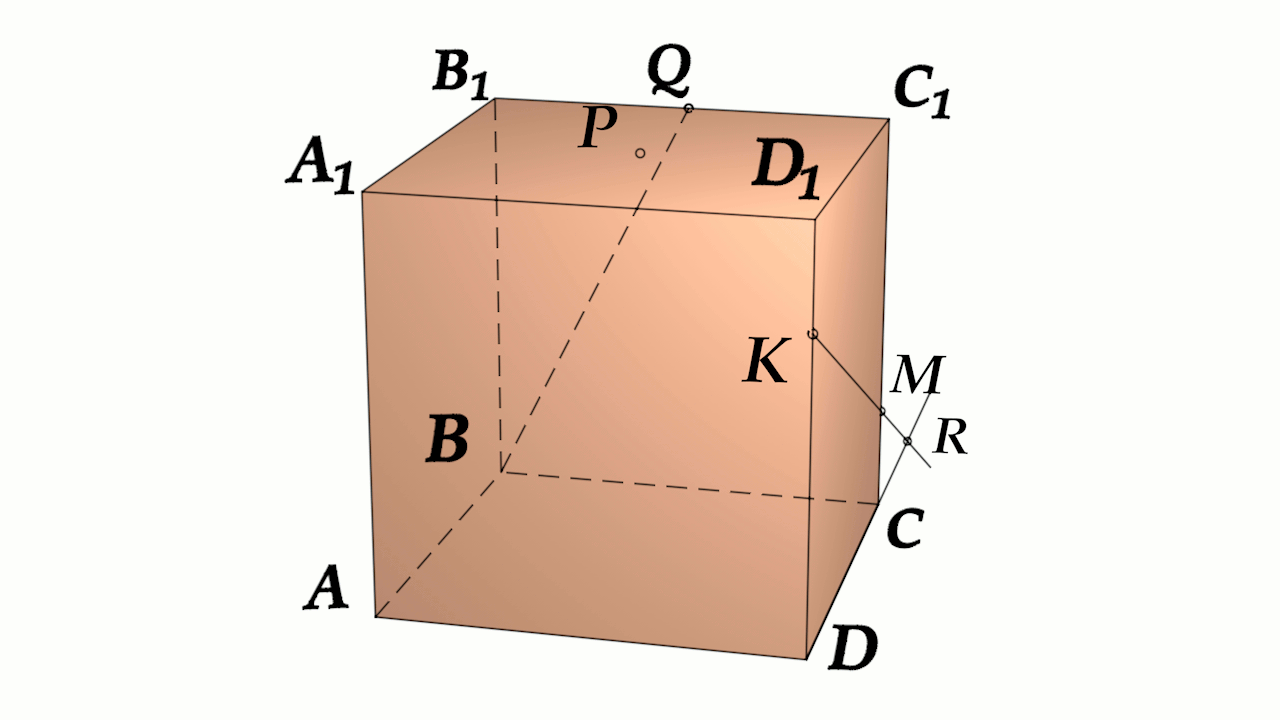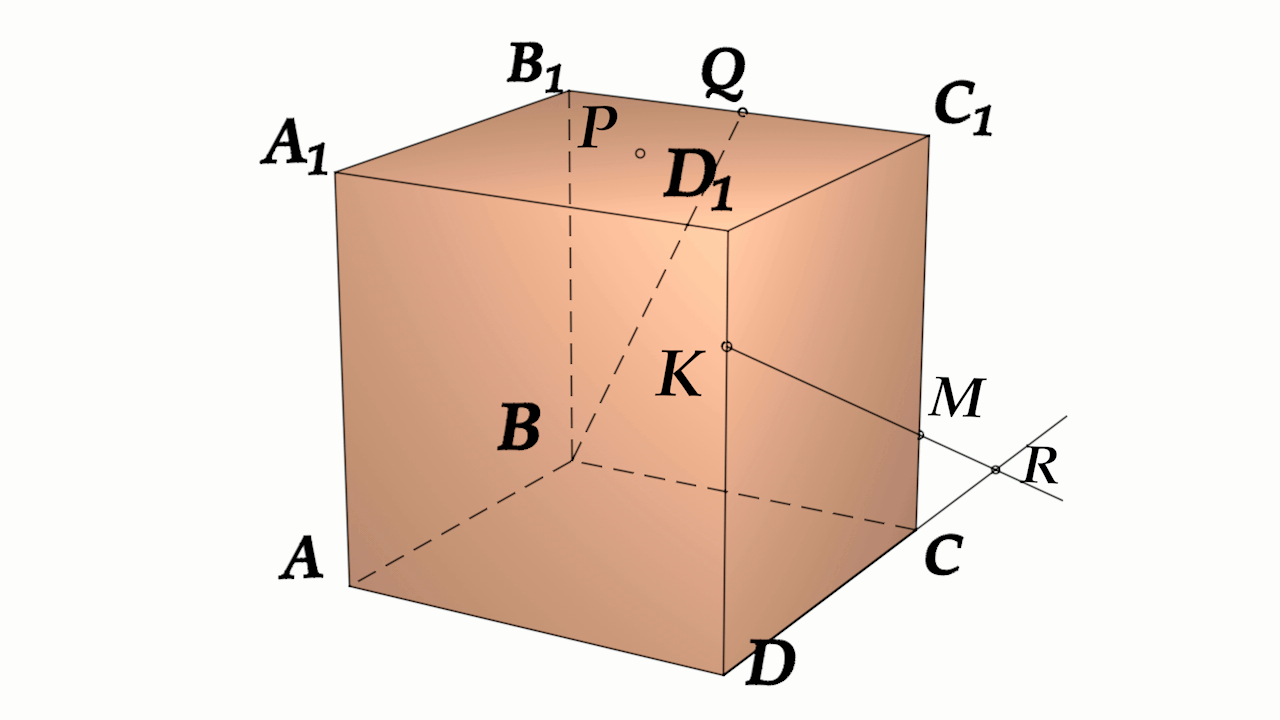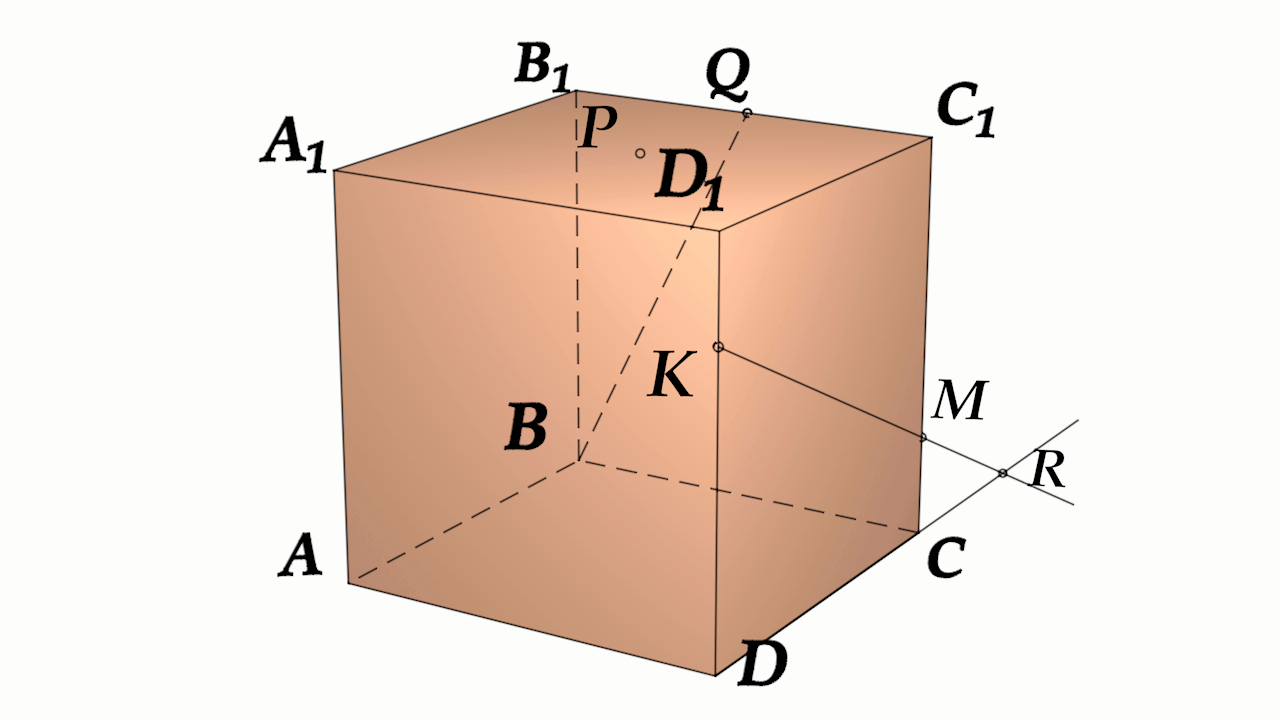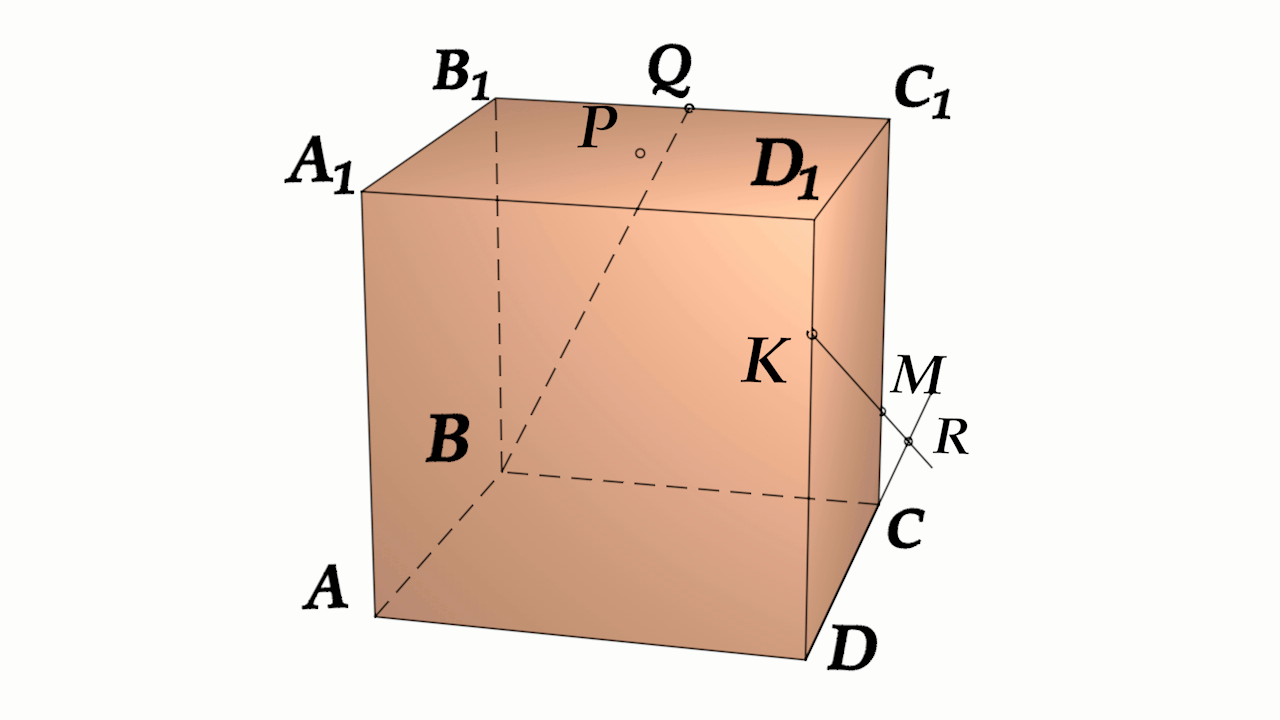
Задача 4: В кубе $ABCD{A_1}{B_1}{C_1}{D_1}$ все ребра равны 1. Точка $Q$ – середина ребра . Точка $K$
делит ребро $D_1D$ в соотношении 1 : 3 считая от вершины $D_1$, а точка $M$ делит $C_1C$ в соотношении
5 : 2 считая от вершины $C_1$. Найти угол между скрещивающимися прямыми $BQ$ и $KM$ .

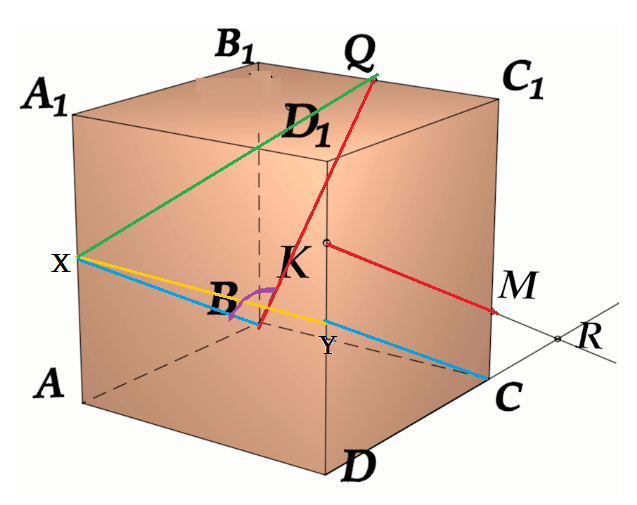
- Параллельными переносами добъемся совмещения в точке $B$. Для этого, перенесем $KM$ в два этапа.
- Сперва соскользим $KM$ по грани $DD_1C_1C$ вдоль $C_1C$ до вершины $C$. Получим отрезок $CYparallel MK$
- Затем, $CY$ протащим параллельно себе вдоль пути $CB$ и перейдем к отрезку $BXparallel CY$.
- В итоге получили то, что надо: $KM$ параллельна $BX$, потому как $MKparallel CYparallel BX$.
- Требуемый угол $angle left(MK;BQright)=angle left(BX;BQright)=angle XBQ$. Найдем его через треугольник $bigtriangleup XBQ$
- В теореме косинусов нам нужны стороны этого треугольника. Вычислим постепенно, шаг за шагом, зная ребро куба 1:
- Из отношения $frac{D_1K}{DK}=frac{1}{3}Rightarrow D_1K=frac{1}{4} DK=frac{3}{4}$. Из отношения $frac{C_1K}{CM}=frac{5}{2}Rightarrow C_1M=frac{5}{7} CM=frac{2}{7}$
- $MKparallel CYRightarrow KY=MC$ отрезок $DY=D_1D-D_1K-KY=1-frac{1}{4}-frac{2}{7}=frac{13}{28}$
- $BXparallel CYRightarrow BX=DY=frac{13}{28}$. По условию задачи $B_1Q=frac{1}{2}$.
- Нужные нам стороны треугольника $bigtriangleup XBQ$ являются гипотенузами прямоугольных треугольников.
- Зная все катеты, как части ребер, по теореме Пифагора найдем стороны $XB$, $BQ$, $XQ$.
- Нужный угол $angle XBQ$ вычислим из теоремы косинусов $XQ^2=XB^2+BQ^2-2cdot XBcdot BQcdot cos angle XBQ$
- наконец: $cos angle XBQ=frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$ $angle XBQ=arccos frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$
- Признак: $XBQ$ – плоскость угла: $KMparallel XBQ$ и $BQin XBQ$
Задача 5: В правильной треугольной призме $ABCMNK$ все ребра равны 2. Точка $D$ делит
ребро $MN$ в отношении 3 : 2 считая от вершины $M$. Найдите угол между прямыми $AD$ и $BK$.
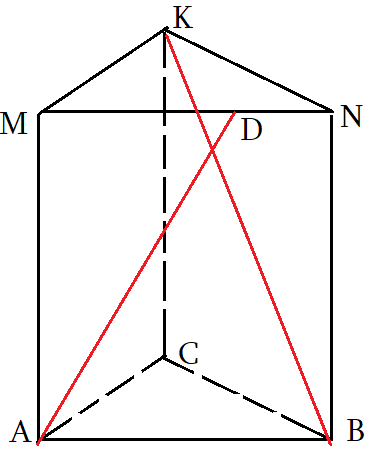
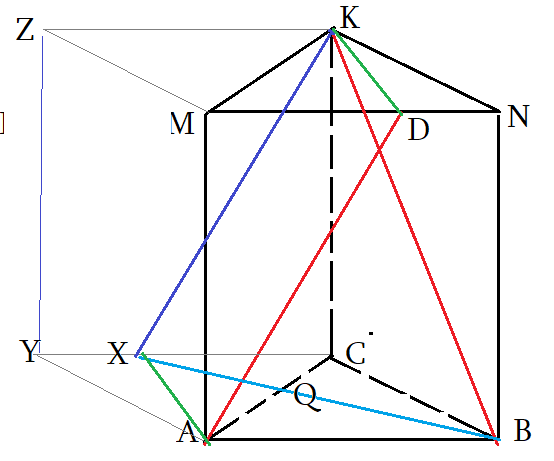
- Чтоб найти угол между скрещивающимися прямыми, нужно “подвигать параллельно” $AD$ и $BK$ до совмещения.
- Если двинуть $AD$ так, чтоб точка $D$ совпала с $K$ – т.е. скользить по плоскости $ADK$, но тогда другой конец $D$ вне рисунка.
- Достроим призму до параллелепипеда $ABCYMNKZ$ и все нужные отрезки, “движения”, плоскости будут внутри!
- $AD$ скользит по плоскости $ADK$ и совпадет с $XK$. Точка $X$, конечно, окажется на ребре $YC$
- по построению: $Xin CDK$ плоскости; $ADparallel XK$ , $XCparallel AB$ . Значит, $XK$ параллельна $AD$
- Угол между прямыми $angle left(AD;BKright)=angle left(XK;BKright)=angle XKB$. Надо найти угол $angle XKB$.
- Угол $XKB$ ищем , как обычно, через треугольник $bigtriangleup XKB$, с помощью теоремы косинусов.
- Для этого надо найти стороны этого треугольника. Сторону $BK$ найдем по Пифагору для треугольника $bigtriangleup BKC$.
- $XC=MD$, найдем $MD$ из отношения 3 : 2 для $MN$ . Затем, по Пифагору $bigtriangleup XKC$ найдем $XK$.
- С вычислением $XB$ придется повозится через теорему косинусов треугольника $bigtriangleup XBC$, две его стороны известны.
- А что с углом $angle XCB$? по условию $bigtriangleup ABC$ равносторонный, значит в параллелограмме $angle YCB=120$ градусов.
- Ну и финально: как только найдем все стороны $bigtriangleup XKB$, мы найдем и его угол $angle XKB$ – то что надо!
- Признак: $XKB$ – плоскость угла: $ADparallel XKB$ и $BKin XKB$
Упражнения:
Координаты вектора
Вектор – отрезок, имеющий длину и указывающий направление.
На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.
Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$
Скрещивающиеся прямые
И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$
Уравнение плоскости
В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.
Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.
Например, пусть даны три точки:
$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$
Подставим координаты точек в общее уравнение плоскости:
$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$
Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.
Теперь у нас есть три уравнения и три неизвестные – можем решить систему:
Пример 3
Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$
Расстояние от точки до плоскости
Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$
Пример 4
Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$
Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$
Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.
Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).
Пример 5
Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.
Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) – середина ребра (CE).
- Докажите, что прямые (AD) и (BG) перпендикулярны.
- Найдите расстояние между прямыми (AD) и (BG).
Решение:
Решим задачу полностью методом координат.
Нарисуем рисунок и выберем декартову систему координат. (Рис 5).
Угол между скрещивающимися прямыми : определение, примеры нахождения
В статье рассматриваются определения угла между скрещивающимися прямыми с приведением графических иллюстраций. При имеющихся координатах направляющих векторов заданных прямых научимся находить искомый угол. В заключительной части решим задачи на нахождение угла.
Угол между скрещивающимися прямыми – определение
Для нахождения искомого угла необходимо пройти несколько этапов.
Две прямые в трехмерном пространстве называются скрещивающимися в случае, если они не находятся в одной плоскости.
Из определения о скрещивающихся прямых следует, что они не являются параллельными или пересекающимися и не совпадают, тогда они находились бы в одной и той же плоскости.
Рассмотрим рисунок, приведенный ниже.

В трехмерном пространстве имеются скрещивающиеся прямые a и b . Проведем прямые а 1 и b 1 параллельные скрещивающимся a и b . Точка М1 является точкой пространства, через которую они проходят. Отсюда получаем, что а1 и b 1 являются пересекающимися прямыми.
Обозначим угол между a 1 и b 1 равным значению α . Построение прямых a 2 и b 2 параллельно скрещивающимися относительно a и b в точке М 2 отличной от М 1 приводит к тому, что значение угла между ними обозначим как α . То есть угол между прямыми a 1 и b 1 равен углу между a 2 и b 2 . В этом можно убедиться, если про/извести параллельный перенос. Тогда точки М 1 и М 2 совпадают.
Углом между скрещивающимися прямыми называют угол, который образуется между двумя параллельными заданными скрещивающимися прямыми.
Отсюда следует, что угол не зависит от точки M и ее выбора. Поэтому точка M может быть любой. Рассмотрим рисунок, приведенный ниже.

Нахождение угла между скрещивающимися прямыми
Угол между скрещивающимися прямыми определяется через угол пересекающихся прямых. Поиск угла сводится к его нахождению между пересекающимися прямыми пространства. Школьные методы решения основываются на необходимости построения на основе подобия фигур или теоремах косинуса, что позволит определить синус, косинус, тангенс угла прямоугольного треугольника.
Удобным способом решения считается нахождение угла методом координат. Рассмотрим его.
Трехмерное пространство имеет прямоугольную систему координат О х у z . Имеется задача, в которой необходимой найти угол α , образованный скрещивающимися прямыми a и b с заданными уравнениями прямых в пространстве.
Для решения необходимо взять произвольную точку в трехмерном пространстве и обозначить буквой M , что дает понять, через нее проходят прямые a 1 и b 1 , которые параллельны скрещивающимся a и b . Угол α , образованными прямыми a и b , из этого определения получится равным пересекающимся a 1 и b 1 .
Для нахождения искомого угла между a 1 и b 1 необходимо использовать формулу для нахождения угла между пересекающимися прямыми, а для этого нужно знать значение координат направляющих векторов у прямых a 1 и b 1 .
Для их получения необходимо применить определение направляющего вектора, которое говорит о том, что множества векторов совпадают. Направляющие векторы прямых обозначают a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) .
Векторы a → и b → имеют координаты, определяющиеся из условия по уравнению или по координатам точек пересекающихся прямых. Тогда получаем, что угол между двумя скрещивающимися прямыми a и b вычисляется из формулы α = a r c cos a → , b → a → · b → = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 , а a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b .
Использование формулы для нахождения косинуса угла между скрещивающимися прямыми а и b дает выражение вида cos α = a → , b → a → · b → = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 .
При помощи основного тригонометрического тождества можно найти синус угла между этими прямыми при известном косинусе из формулы sin α = 1 – cos 2 α .
Найти угол между скрещивающимися прямыми a и b , которые заданы уравнениями x 2 = y – 4 0 = z + 1 – 3 и x = 1 + λ y = 1 – λ z = – 3 + 4 · λ , λ ∈ R и определяются в системе координат О х у z .
Для определения координат необходимо использовать каноническое уравнение прямой в плоскости. необходимо обратить внимание на знаменатель дробей. Отсюда видно, что a → = ( 2 , 0 , – 3 ) является направляющим вектором прямой x 2 = y – 4 0 = z + 1 – 3 . При наличии параметрического уравнения можно определить координаты направляющего вектора, так как она равняются коэффициентам, тогда получаем, что b → = ( 1 , – 1 , 4 ) является направляющим вектором для прямой вида x = 1 + λ y = 1 – λ z = – 3 + 4 · λ , λ ∈ R .
Отсюда получаем, что имеются все необходимые формулы и данные для того, чтобы произвести вычисление угла между скрещивающимися прямыми. Имеем, что
α = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 = a r c cos 2 · 1 + 0 · ( – 1 ) + ( – 3 ) · 4 2 2 + 0 2 + ( – 3 ) 2 · 1 2 + ( – 1 ) 2 + 4 2 = = a r c cos 10 13 · 18 = a r c cos 10 3 26
Ответ: угол между скрещивающимися прямыми равен a r c cos 10 3 26 .
Найти значение синуса и косинуса угла между скрещивающимися прямыми, где имеются ребра A D и В С , принадлежащие пирамиде A B C D , с известными вершинами с координатами A ( 0 , 0 , – 1 ) , B ( 5 , 7 , – 5 ) , C ( 3 , 7 , – 5 ) , D ( 1 , 3 , 1 ) .
A D → и B C → являются векторами соответствующих сторон заданной фигуры. Необходимо вычислить координаты с помощью имеющихся данных начала и конца.
Получаем, что A D → = ( 1 – 0 , 3 – 0 , 1 – ( – 1 ) ) ⇔ A D → = ( 1 , 3 , 2 ) B C → = ( 3 – 5 , 7 – 7 , – 5 – ( – 3 ) ) ⇔ B C → = ( – 2 , 0 , – 2 )
Из формулы cos α = a r c cos A D → , B C → A D → · B C → находим косинус угла между заданными скрещивающимися прямыми. Получаем выражение вида
cos α = 1 · ( – 2 ) + 3 · 0 + 2 · ( – 2 ) 1 2 + 3 2 + 2 2 · ( – 2 ) 2 + 0 2 + ( – 2 ) 2 = 6 14 · 8 = 3 2 7
Перейдем к вычислению синуса угла между этими прямыми. Подставляем значения и получаем, что sin α = 1 – cos 2 α = 1 – 3 2 7 2 = 19 2 7 .
Ответ: sin α = 19 2 7 , cos α = 3 2 7 .
В заключительном этапе рассмотрим задачу, в которой нужно найти угол между скрещивающимися прямыми с самостоятельно введенной системой координат.
Имеется прямоугольный параллелепипед A B C D A 1 B 1 C 1 D 1 со сторонами А В = 3 , А D = 2 и A A 1 = 7 единиц. Точка E делит прямую А А 1 как 5 : 2 . Определить угол между скрещивающимися прямыми В Е и А 1 С .
Ребра заданного параллелепипеда являются взаимно перпендикулярными, поэтому необходимо ввести прямоугольную систему координат для определения угла между указанными скрещивающимися прямыми с помощью метода координат.
Для начала вводится прямоугольная система координат О х у z . Получаем, что начало координат является совпадающим с вершиной A , а О х совпадает с прямой A D , О у с A B , а О z с А А 1 . Рассмотрим рисунок, приведенный ниже.

Отсюда имеем, что точка B с координатами ( 0 , 3 , 0 ) , E – ( 0 , 0 , 5 ) , A А – ( 0 , 0 , 7 ) , C – ( 2 , 3 , 0 ) . Исходя из координат, мы можем получить координаты векторов B E → и A 1 C → , необходимые для дальнейшего решения задачи. Получаем, что B E → = ( 0 , – 3 , 5 ) , A 1 C → = ( 2 , 3 , – 7 ) .
Применим формулу для нахождения угла, образованного скрещивающимися прямыми, при помощи координат направляющих векторов. Получаем выражение вида
α = a r c cos B E → , A 1 C → B E → · A 1 C → = a r c cos 0 · 2 + ( – 3 ) · 3 + 5 · ( – 7 ) 0 2 + ( – 3 ) 2 + 5 2 · 2 2 + 3 2 + ( – 7 ) 2 = = a r c cos 44 34 · 62 = a r c cos 22 527
Научно-исследовательская работа “Нахождение угла между скрещивающимися прямыми”
«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику

5.Список используемой литературы
В представленной работе исследуются методы нахождения угла между скрещивающимися прямыми. Решая тесты ЕГЭ, обратил внимание на то, что в них присутствуют задачи такого типа и не всегда их можно решить, используя только один метод. Решая задачи, я всегда ищу более короткое, рациональное, наиболее красивое решение.
Эта работа актуальна потому что, исследуя методы на нахождение угла между скрещивающимися прямыми, у меня появилась возможность расширить полученные на уроках знания, научиться решать задачи новыми способами, а в дальнейшем применять эти знания на олимпиадах и заданиях ЕГЭ. Предметом моих исследований стали геометрические задачи на нахождение угла между скрещивающимися прямыми.
Рассмотреть теоретический аспект угла между скрещивающимися прямыми.
Обобщить все знания, полученные в ходе исследования.
Изучить литературу по данной теме.
Познакомиться с новыми методами нахождения угла между скрещивающимися прямыми.
Подобрать задачи по данной теме.
Исследовать задачи на примере изученных методов и находить наиболее рациональное решение.
Гипотеза: С помощью изученных методов можно найти наиболее рациональное решение олимпиадных задач и заданий ЕГЭ – С2».
Определение: Прямые не лежащие в одной плоскости называются скрещивающимися (см. Рис.1).
Теорема: Если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке не лежащей на первой прямой, то эти прямые скрещивающиеся.

Рисунок 1. Скрещивающиеся прямые.
Угол между скрещивающимися прямыми.
Определение: Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, параллельными данным скрещивающимся прямым (см. рис 2).

Рисунок 2. Угол между скрещивающимися прямыми b и a .
Способы нахождения угла между скрещивающимися прямыми.
Первый способ — с помощью параллельного переноса. Напомним, в чем его суть: мы производим перенос одной из скрещивающихся прямых (или сразу двух) так, чтобы прямые, полученные в результате этого преобразования, пересекались. Тем самым исходная задача сводится к нахождению угла между двумя прямыми на плоскости.
Определение типа прямых.
Параллельный перенос одной или обеих прямых.
Нахождение требуемого угла.
а) Пусть а и b – данные скрещивающиеся прямые. Через одну из них, например, b и через какую-нибудь точку А, лежащую на прямой а, проведем плоскость α.
б) Через точку А проведем прямую с|| b . Получившийся ∠ MAN – угол между скрещивающимися прямыми.
в) Выберем на прямой а – какую-нибудь точку М , а на прямой с – точку N . Получим треугольник AMN . Вычислим стороны треугольника по теореме косинусов и найдем .

Рисунок 3. Поэтапно-вычислительный метод.
Метод трех косинусов.
Определить тип прямых.
Спроектировать скрещивающуюся прямую на плоскость.
Нахождение искомого угла.
Пример (см. рис. 4).
а) а и b -скрещивающиеся прямые. Проведем через прямую а плоскость α пересекающую прямую b .
б) Спроектируем b на α . b 1 – проекция.

Рисунок 4. Метод трех косинусов.
Метод проектирования обеих скрещивающихся прямых на плоскость перпендикулярную одной из них.
Пример (см. рисунок 5).
а) а и b – скрещивающиеся прямые.
б) Плоскость α перпендикулярна прямой а, b пересекает α в точке В, точка А – проекция прямой а, а прямая b 1 проекция прямой b .
в) На прямой b лежит отрезок длинной d , а его проекция на плоскость α имеет длину d 1.
г) Тогда верна формула , где α – угол между прямыми а и b .

Рисунок 5. Метод проектирования обеих скрещивающихся прямых на плоскость перпендикулярную одной из них.
Метод проектирования отрезка одной из скрещивающихся прямых на другую (см. прил. 9).
а) a и b – скрещивающиеся прямые.
б) На прямой a находится отрезок длины d , и его ортогональной проекцией на прямую b является отрезок длиной d 1.
в) Тогда верна формула , где α – угол между прямыми a и b .

Рисунок 6. Метод проектирования отрезка одной из скрещивающихся прямых на другую.
Весьма эффективный метод, но встречается достаточно редко.
Пример (см. рис. 7).
Для тетраэдра верна формула .

Рисунок 7. Метод тетраэдра.
Я подробней остановлюсь на самом универсальном на мой взгляд, самом доступном для понимания, координатном методе.
На рисунке изображаем указанные в задаче прямые (которым придаем направление, т.е. векторы).
Вписываем фигуру в систему координат.
Находим координаты концов векторов.
Находим координаты Векторов.
Подставляем в формулу “косинус угла между векторами”.
После чего (если требуется в задаче), зная косинус, находим значение самого угла.
Чтобы освоить этот метод, надо хорошо уметь находить координаты точки в пространстве и правильно располагать многогранники в системе координат. Более подробно с расположением стереометрических фигур в системе координат вы можете ознакомиться в приложение (см. прил. 1-6).
Формула косинуса угла между векторами.
Задача №1. На ребре ВВ 1 куба ABCDA 1 B 1 C 1 D 1 взята точка К так, что BK:KB 1 =3:1. Найдите угол между прямыми AK и BD 1 (см. рис.8).

Рисунок 8. Задача №1.
1) AK и BD 1 – скрещивающиеся прямые.
2) Д.П. достроим куб до призмы A1B1C1D1A2B2C2D2, где ABCDA2B2C2D2-куб. Отметить точку Е на АА1 так, что АЕ : ЕА2=3:1. Тогда AK параллельна BE. Рассмотрим треугольник EBD1. Возьмем сторону АВ=1; BE =1.25 (по теореме Пифагора).
3), по правилу параллелепипеда.
4), по теореме Пифагора.
по теореме косинусов.
5)Получим , где α искомый угол.
Пример решения этой же задачи можете пронаблюдать в приложение (см.прил.7-8).
Задача №2. В правильный 4-х угольной призме ABCDA 1 B 1 C 1 D 1 сторона основания равна 2,боковое ребро равно 1. Найдите угол между АА 1 и B 1 D(см.рис.9).

Рисунок 9. Задача №2.
АА 1 и B 1 D – скрещивающиеся прямые.
т. А – проекция АА 1 , на плоскость ABC .
BD – проекция BD 1 -на АВС, тогда
Задача №3. В правильной 6-ти угольной пирамиде АВС…F 1 сторона основания равна корню квадратному из 2-х, а боковое ребро равно 1. Найдите угол между АF 1 и B 1 C(см. рис. 10).

Рисунок 10. Задача №3
AF 1 и B 1 C – скрещивающиеся прямые.
F 1 A || BO , где O -центр 6-ти угольника ABCDEF .
Рассмотрим тетраэдр OBB 1 C :, по теореме Пифагора; в правильном треугольнике OB 1 A 1; BB 1 =1; BC = по условию
Задача №4. В правильной треугольной призме все ребра равны 1. Найдите угол между прямыми A С 1 и С B 1 .
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 967 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 340 человек из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 691 человек из 74 регионов
Ищем педагогов в команду «Инфоурок»
- Щербакова Татьяна ИвановнаНаписать 6590 14.04.2016
Номер материала: ДБ-032565
-
14.04.2016 417
-
14.04.2016 261
-
14.04.2016 328
-
14.04.2016 1703
-
14.04.2016 266
-
14.04.2016 1476
-
14.04.2016 450
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Россия направит $10,3 млн на развитие школьного питания в нескольких странах
Время чтения: 1 минута
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Число участников РДШ за 2021 год выросло в три раза
Время чтения: 2 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Проблемно-реферативный прект “Углы в пространстве”

В работе рассмотрены 4 способа нахождения угла между скрещивающимися прямыми:
-С помощью параллельного переноса
-Способ «в три косинуса»
Решаются и исследуются задания С2 из вариантов ЕГЭ на нахождение угла между скрещивающимися прямыми.
Проект содержит реферат по теме и презентацию.
Скачать:
| Вложение | Размер |
|---|---|
| ugol_mezhdu_skreshchivayushchimisya_pryamymi.pptx | 2.74 МБ |
| ugol_mezhdu_skreshchivayushchimisya_pryamymi.docx | 2.25 МБ |
Предварительный просмотр:
Подписи к слайдам:
Выполнил : Гладков Дмитрий ученик 11 класса МАОУ СОШ №58 п. Мулино Володарский район Нижегородская область Руководитель : Байгулова Нина Витальевна учитель математики МАОУ СОШ №58 Углы в пространстве
Угол между прямой и плоскость Угол между плоскостями Угол между скрещивающимися прямыми
Введение Вопросы инновационных технологий в строительстве, космонавтике, технике невозможны без умения производить необходимые чертежи и вычисления, которые требуют знания важных и интереснейших свойств геометрических фигур.
Геометрия в природе В живой природе функция и форма тесно сближены и взаимно обусловлены.
Цели проекта: Обобщить и систематизировать знания, умения и навыки по теме «Многогранники». Иметь представление о типах заданий С2 в вариантах ЕГЭ. Отработать приёмы и методы построения искомого на чертеже. Подготовиться к ЕГЭ.
Задачи проекта: Формирование прочных навыков решения задач по теме: «Углы между скрещивающимися прямыми». Приобрести умение пользоваться справочной и научной литературой. Научиться рассуждать научно и логически.
Содержание ВВЕДЕНИЕ ОСНОВНАЯ ЧАСТЬ Глава1.Справочный материал §1. Из истории геометрии §2.Полезно знать Глава 2.Способы нахождения углов между скрещивающимися прямыми §3. Параллельный перенос 3.1 Куб 3.2.Шестигранная призма §4. Метод координат 4.1. Координаты куба 4.2. Координаты трехгранной призмы 4.3. Координаты шестигранной призмы 4.4. Координаты четырехугольной пирамиды §5. Способ «в три косинуса» §6. Правило тетраэдра Глава 3. Практическое приложение: «Задания С2 ЕГЭ» §7. Три способа решения одной задачи С2 7.1. Решение 1 (по теореме о 3 перпендикулярах) 7.2. Решение 2 (параллельный перенос) 7.3. Решение 3(метод координат) §8. Решите сами ЗАКЛЮЧЕНИЕ ИСТОЧНИКИ МАТЕРИАЛОВ
Геометрия применялась при постройке величественных сооружений, которые стоят и по сей день. Пирамиды Хеопса Колизей Амфитеатр Пирамида Майя Геометрия в древности
Н. И. Лобачевский Леонард Эйлер Пьер Ферма Евклид Пифагор К.Ф. Гаусс Люди, принявшие участие в создании геометрии как науки
Углом между скрещивающимися прямыми
Полезно знать Прямые называются скрещивающимися, если они не пересекаются и лежат в разных плоскостях. а в α β
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся. a b b M m n
(теорема косинусов) При нахождении угла между пересекающимися прямыми используют формулу Полезно знать a b c
A B C a b c гипотенуза катет катет Прямоугольный треугольник Теорема Пифагора Площадь Если А=30 ˚ , то Если А=45 ˚, то sin A= cos A= tg A= ctgA = с² = а² + b ² S =0,5а ∙ b а =c : 2 а =b а :c b:c а :b b : a S =0,5 с ∙ h c
Правильный треугольник Стороны Углы Площадь Периметр О – точка пересечения 60 ˚ 60 ˚ 60 ˚ а а а О равны равны 60 ˚ S =а²√3:4 высот, медиан, биссектрис, центр вписанной и описанной окружности Р = 3а r R R =2 r =2/3 h= a : √3
Правильный четырёхугольник – квадрат Стороны Углы Площадь Периметр Диагонали О – точка пересечения диагоналей 90 ˚ 90 ˚ 90 ˚ 90 ˚ равны 90 ˚ равны S =а² Р = 4а равны, перпендикулярны, биссектрисы углов центр вписанной и описанной окружности О R r R = 1/ 2 d= a √2 :2; r = 1/2 a
Правильный шестиугольник Стороны Углы Периметр Площадь Диагонали О – точка пересечения диагоналей 60 ˚ 60 ˚ 60 ˚ 120 ˚ равны равны 120 ˚ Р = 6а S =3а²√3:2 равны, биссектрисы углов а центр вписанной и описанной окружности R r О R = а ; r = a √3:2 3 0 ˚
Призма ТРЕУГОЛЬНАЯ ЧЕТЫРЁХУГОЛЬНАЯ ШЕСТИУГОЛЬНАЯ
Пирамида ТРЕУГОЛЬНАЯ (тетраэдр) ЧЕТЫРЁХУГОЛЬНАЯ ШЕСТИУГОЛЬНАЯ
Способы нахождения угла между скрещивающимися прямыми С помощью параллельного переноса Метод координат Способ «в три косинуса» Правило тетраэдра α b a
Параллельный перенос № 1
Точку М можно выбрать произвольным образом. В качестве точки М удобно взять любую точку на одной из скрещивающихся прямых. a b M m Полезно знать
D D 1 А А 1 В В 1 С С 1 1 1 1 1 Прямая AD 1 параллельна прямой ВС 1 , АВ 1 = AD 1 = В 1 D 1 =√ 1²+1²=√2, Угол между п рямыми АВ 1 и ВС 1 равен ∠ В 1 AD 1 . Ответ: 60. Задача 1. В единичном кубе АВС D А 1 В 1 С 1 D 1 найдите угол между прямыми АВ 1 и ВС 1 . Решение (параллельный перенос) ∆ В 1 AD 1 – равносторонний, В 1 AD 1 = 60 0.
Задача 2. В кубе ABCDA ₁ B ₁ C 1 ₁ D 1 ₁ все ребра равны 1. Найдите угол между прямыми АВ и CB 1 ₁ A C B D A A 1 D 1 C 1 B 1 Ответ:90 1 1 1 Угол между прямыми АВ и C В₁ равен углу между СВ₁ и CD . Решение (параллельный перенос) D СВ₁ =90°.
Задача 3. В кубе ABCDA ₁ B ₁ C ₁ D ₁ все ребра равны 1. Найдите угол между прямыми C А и BD ₁ . A C B D A 1 D 1 C 1 B 1 C 2 B 2 D C 3 B 3 Ответ:90. 1 1 1 √5 √3 √2 √2 Угол между прямыми АС и BD ₁ равен углу D ₁ВС₂ . 1 Решение (параллельный перенос)
Задача4. В правильной шестиугольной призме ABCDEFA ₁ B ₁ C ₁ D ₁ E ₁ F ₁ все ребра равны 1. Найдите угол между прямыми АВ и A ₁С ₁ A B C D E F A 1 F 1 E 1 D 1 C 1 B 1 Ответ:30 120 ° 1 1 1 Решение (параллельный перенос) Δ АВС – равнобедренный, АВС = 120 0 . САВ = 30 0
1 1 1 А В С D Е F А 1 В 1 С 1 D 1 Е 1 F 1 О О 1 А В С D Е F А 1 В 1 С 1 D 1 Е 1 F 1 Построим плоскость А 1 D 1 D параллельную плоскости ВВ 1 С 1 С. Прямая AO 1 ll BC 1 . Задача 5 . В правильной шестиугольной призме A … F ₁ , все ребра которой равны 1, найдите косинус угла между прямыми AB 1 и BC 1 . Решение (параллельный перенос) √2 √2 1 AO 1 = √2, AB 1 = √2. B 1 O 1 = 0,5 B ₁E₁ = 1. Искомый угол между прямыми AB 1 и BC 1 равен B 1 AO 1 . Ответ: 0 ,75
Метод координат № 2
О А В С ( х ₁; у₁; z₁ ) ( х ₂; у₂ ; z₂ ) ( х ; у ;z ) Длина отрезка: АВ=√ ( х₁-х ₂)²+( у₁-у ₂)² +(z₁-z₂)² Координаты середины отрезка: х= ( х₁+х ₂):2 ; у= ( у₁+у ₂):2 ; z=(z₁+z₂):2 Полезно знать х у z
Координаты вектора АВ Длина вектора АВ Координаты суммы а + b Координаты разности а – b Координаты вектора умноженного на число: Полезно знать В( х ₁; у₁; z ₂ ) А( х ₂; у₂ ; z ₂ ) а( х ₁ ; у ₁; z₁ ) b ( х ₂ ; у ₂; z ₂ ) k а( k х ₁ ; k у ₁; k z ₁ ) k а х у ( х = х ₁ – х ₂ ; у = у ₁ – у ₂; z₁ – z ₂ ) = √х² + у²+ z ² ( х₁ + х₂ ; у₁ + у ₂; z₁ + z₂ ) ( х₁ – х₂ ; у₁ – у ₂; z₁ – z₂ ) ( k х ₁ ; k у ₁; k z ₁ ) z
Угол между двумя прямыми равен углу между их направляющими векторами a (x 1 ; y 1 ; z 1 ) и b (x 2 ; y 2 ; z 2 ). Косинус угла между векторами: a b
Координаты куба Точка A B C D Координаты Точка A 1 B 1 C 1 D 1 Координаты 1 1 1 х у Z A B C D A ₁ B ₁ C ₁ D ₁ (0; 0; 0) (1; 0; 0) (1; 1; 0) (0; 1; 0) (0; 0; 1) (1; 0; 1) (1; 1; 1) (0; 1; 1)
D D 1 А А 1 В В 1 С С 1 1 1 1 1 Введем систему координат. н айдём cos = 1/2 Ответ: 60 З адача1. В единичном кубе АВС D А 1 В 1 С 1 D 1 найдите угол между прямыми АВ 1 и ВС 1 . Решение (метод координат) х у z Координаты точек: А(0; 0; 0), В ₁ (1; 0; 1), П о формуле Координаты векторов: АВ ₁ (1 ; 0; 1 ), ВС ₁ (0; 0; 1). В(1 ; 0; 0 ), С ₁ (1; 1; 1). ( А В 1 ;ВС 1 )=60 0 .
Способ «в три косинуса» № 3
a b b 1 Cos ab =Cos ab 1 · Cos bb 1 Полезно знать
Решение (способ «в три косинуса ») D D 1 А А 1 В В 1 С С 1 Cos ( AB₁ , BC₁ ) = Cos AB₁B · Cos B₁BC₁ Построим проекцию ребра АВ 1 на плоскость ( B 1 BC) . Применяя формулу: получаем : Cos ( AB 1 , BC 1 ) =0 , 5 . З адача1. В единичном кубе АВС D А 1 В 1 С 1 D 1 найдите угол между прямыми АВ 1 и ВС 1 . ( AB ₁ , BC ₁ ) = 60 °. 1 √2 1 1 √2 Ответ: 60
№ 4 С помощью тетраэдра
D А В С 2 l ( AC ² + BD ² )-( CD ² + AB ² ) l Cos( AD , CB ) = AD · CB Полезно знать
D D 1 А А 1 В В 1 С С 1 2 ( BB ₁² + AC ₁² )-( AB ² + B ₁ C ₁² ) Cos( AB ₁ , BC ₁ ) = AB 1 · BC 1 Построим тетраэдр с противоположными ребрами AB 1 и BC 1 . Применяя формулу, Получаем: Cos ( AB ₁ ,BC ₁ ) =0 , 5 . Решение (с помощью тетраэдра) З адача1. В единичном кубе АВС D А 1 В 1 С 1 D 1 найдите угол между прямыми АВ 1 и ВС 1 . 1 1 1 √3 √2 √2 ( AB ₁ ,BC ₁ ) = 60 °. Ответ: 60
Практикум: « Решение задач С2 ЕГЭ» Нахождение угла между скрещивающимися прямыми
Найдите несколько способов решения задачи Задача6. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите угол между прямыми AB 1 и BE 1 .
Ответ: 90 Так как А₁ E 1 А₁В₁ , то А₁ E 1 перпендикуляр к плоскости АА₁В₁, следовательно A 1 B проекция наклонной BE 1 . АВ₁ А ₁B (диагонали квадрата) . Следовательно BE 1 АВ₁ (по теореме о трёх перпендикулярах). Решение 1 ( по теореме о трёх перпендикулярах). Τ Τ Τ Значит ∠ ( АВ₁ ;ВЕ₁ )= 90°.
Решение 2 (параллельный перенос) . Ответ: 90 G 1 2 1 √5 1 1 √3 √7 √2 √2 Построим В G 1 ||АВ₁ . Тогда В G 1 = АВ₁ = √2. ∆ВЕЕ₁ прямоугольный и ВЕ=2, ЕЕ₁=1 , то ВЕ₁=√5 (по теореме Пифагора). Е₁А₁ А₁В₁ , Е₁А₁=√3 , А₁ G 1 =2, то Е₁ G 1 =√7 (по теореме Пифагора). Для ∆ВЕ₁ G 1 проверим теорему Пифагора: √7² =√5²+√2². Значит ∠ Е₁В G 1 =90°. 1 1 Τ
Решение 3 (метод координат). Х Z У Ответ: 90 (1, 0, 0) (0 , √3 , 1) ( 0 , 0, 0) Введем систему координат . Вектор АВ₁(1, 0, 1). Вектор ВЕ₁ (-1, √3, 1). Найдём cos ∠ ( АВ₁ ;ВЕ₁ )=0. Найдём координаты точек: А, В, В₁, Е₁. (1, 0, 1) Значит ∠ ( АВ ₁ ; ВЕ ₁ )= 90°.
Задания С2 ЕГЭ (решите сами) 1.В кубе ABCDA 1 B 1 C 1 D 1 отмечены точки E и F — середины ребер A 1 B 1 и B 1 C 1 соответственно. Найдите угол между прямыми AE и BF. 2. Ребро куба равно 4. Найдите косинус угла между прямыми PQ и EF , P – середина АА1, Q – середина С1 D 1 , Е – середина ВВ1, F – середина DC . 3. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите косинус угла между прямыми AB 1 и BD 1 . 4. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите синус угла между прямыми ВМ и DE, где М — середина ребра SC. 5. В правильной треугольной призме ABCA₁В₁С₁, все рёбра которой равны 1,найдите расстояние между прямыми AA₁ и BC₁. . Ответ: arccos 0,8. Ответ: 1/3. Ответ: 0,25 √2 . Ответ:1 . Ответ: 0,5 √3 .
Заключение Исследование и решение мною заданий С2 ЕГЭ показало, что есть множество способов нахождения углов между скрещивающимися прямыми. Заметил, что для каждой задачи, можно найти рациональный метод решения. Мою работу можно использовать при подготовке к ЕГЭ , при отработке навыков решения заданий C2 .
http://img-fotki.yandex.ru/get/3108/lelbka-saf.1/0_5577_d07190c7_L.jpeg http://img-fotki.yandex.ru/get/27/sm-lydmila.17/0_17993_f3a34074_-1-L.jpeg http://img-fotki.yandex.ru/get/3314/promza-03.3/0_26186_f5ddd573_L.jpeg http://img-fotki.yandex.ru/get/3211/zvyg-ov.0/0_4606_1f62c48f_L.jpeg http://img-fotki.yandex.ru/get/3303/sharlen59.11/0_1c33b_185e1b1e_L.jpeg http://img-fotki.yandex.ru/get/37/hvosttruboi.0/0_1be5b_9345420c_L.jpeg http://img-fotki.yandex.ru/get/3311/mik3966.2/0_20b58_2f399108_L.jpeg http://img-fotki.yandex.ru/get/2709/tlitvintseva.0/0_1e455_859da4e0_L.jpeg http://img-fotki.yandex.ru/get/52/yealaguna.4/0_f425_b6e64384_L.jpeg http://img-fotki.yandex.ru/get/19/galamish.6/0_dbab_144f93ff_L.jpeg http://alexlarin.net/ege11.html И.Р. Высоцкий « Самое полное издание типовых вариантов заданий ЕГЭ» Москва « Астрель », 2010г. Г.И. Глейзер,« История математики в школе», Москва , « Просвещение» ,1982г. Л.И.Звавич , А.Р.Рязановский «Геометрия в таблицах 7-11 классы» Москва. Издательский дом «Дрофа» ,2005г. А.Л. Семенова и И.В. Ященко «ЕГЭ. Универсальные материалы для подготовки учащихся», Ярославль « Интеллект-центр», 2011г. В.А.Смирнов «Готовимся к ЕГЭ. Геометрия. Стереометрия»– М.:МЦНМЩ,2011 Источники материалов
Спасибо за внимание! «Жизнь не спросит, что ты учил. Жизнь спросит, что ты знаешь»
[spoiler title=”источники:”]
http://infourok.ru/nauchnoissledovatelskaya-rabota-nahozhdenie-ugla-mezhdu-skreschivayuschimisya-pryamimi-1032917.html
http://nsportal.ru/ap/library/drugoe/2015/12/17/prezentatsiya-k-prektu-ugly-v-prostranstve
[/spoiler]
