Чтобы найти косинус угла по клеточкам, следует вспомнить, что это собственно за величина – косинус.
По определению, косинус – это отношение прилежащего катета к гипотенузе.
Зная это определение мы очень легко можем найти косинус любого прямоугольного треугольника, нарисованного на клеточках. То есть если задан просто угол, мы достраиваем его до прямоугольного треугольника:

Разберем несколько случаев.
Катеты расположены вертикально и горизонтально. Тогда их длину определяем по клеточкам, а длину гипотенузы по теореме Пифагора.
Катеты расположены произвольно. Заключаем треугольник в прямоугольник и находим катеты и гипотенузу по теореме Пифагора для всех трех сторон. Дальше находим косинус как отношение по определению.

Например здесь катет АО находится как корень из 20 (16+4). Гипотенуза ОВ находится как корень из 37 (36+1). Их отношение – косинус угла АОВ.
Если треугольник АОВ не получается прямоугольным, то имеет смысл использовать теорему косинусов:

![]()
Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):
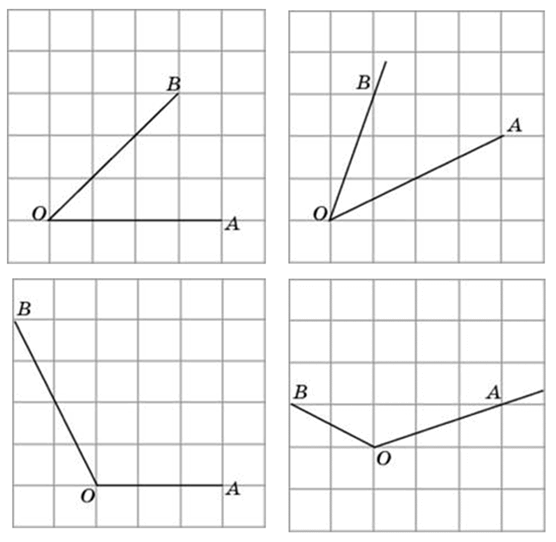
Итак, рассмотрим задание:

Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.
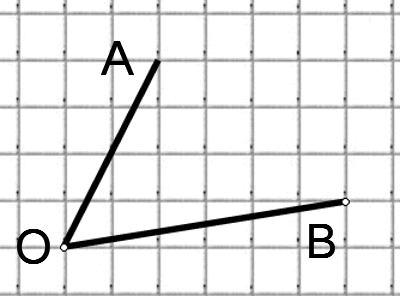
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.
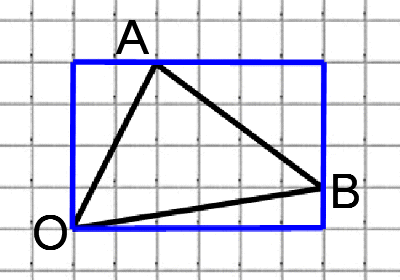
Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).
АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,
![]()
ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,
![]()
OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,
![]()
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
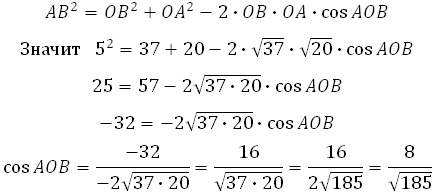
Из основного тригонометрического тождества можем найти sin AOB:
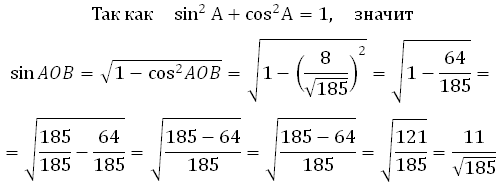
*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.
Теперь можем найти тангенс:
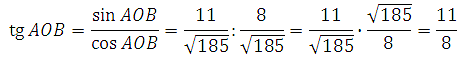
Умножим результат на 8 и запишем ответ:
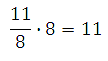
Ответ: 11
Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.
Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
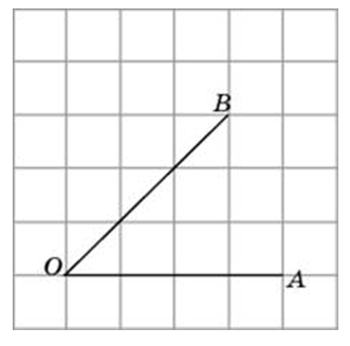
Посмотреть решение
Найдите тангенс угла AOB.
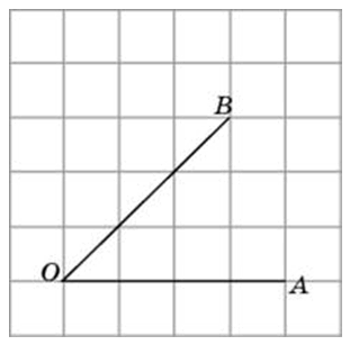
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.
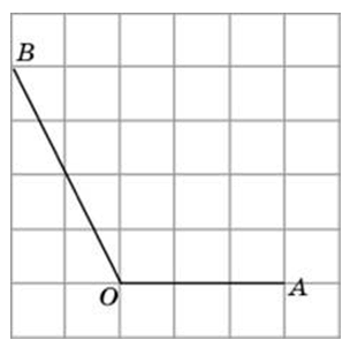
Посмотреть решение
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.
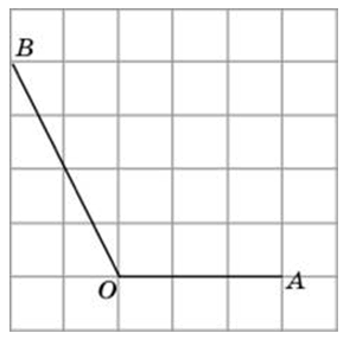
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
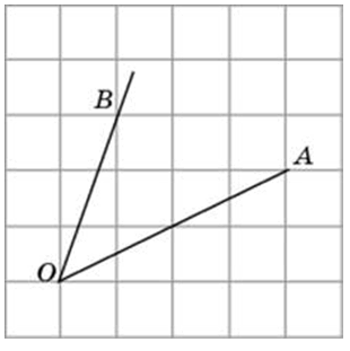
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.
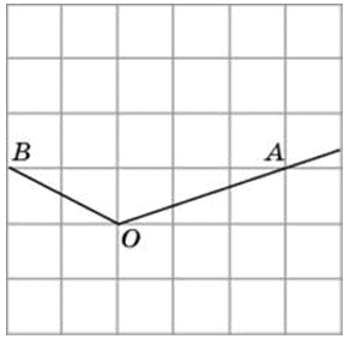
Посмотреть решение
Найдите тангенс угла AOB.
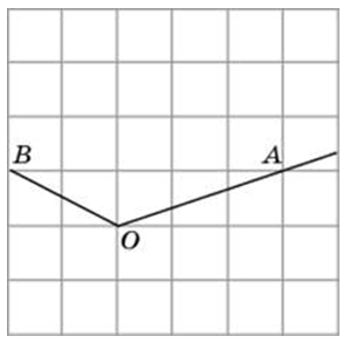
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях )
Один из типов задач в задании 3 – это задачи на нахождение углов.
На клетчатой решетке изображен угол, величину которого надо найти.
Это могут быть самые разнообразные углы:
Методы вычисления могут быть разные.
Принцип большинства заданий – найти прямоугольный треугольник и вычислить у него стороны и найти угол используя синус или косинус или тангенс (в зависимости от задания)
Если необходимо найти тангенс тупого угла, то в начале находим тангенс смежного острого угла и применяем формулу приведения (в ответе появится минус). Напомню, что синус тупого и острого угла имеет один и тот же знак, а вот косинус, так же как и тангенс, тупого и острого угла имеет противоположные знаки.
Если так не получается, то начинаем искать отрезки, треугольники и вычислять стороны. Применять свойство равнобедренных треугольников или теорему косинусов.
Если совсем непонятно, что делать, то встройте угол в прямоугольник и посчитайте все стороны и решение придет
Мы рассмотрели один из типов задач. Главное, поймите принцип, а тогда решите любую задачу.
Задача 53690 на клетчатой бумаге с размером клетки…
Условие
![]()
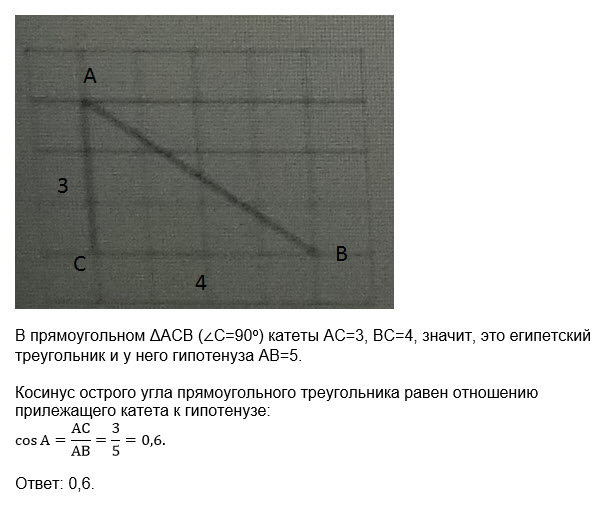
на клетчатой бумаге с размером клетки 1х1 изображён угол, найдите косинус этого угла

математика
4466
Решение
![]()
★
Все решения
![]()
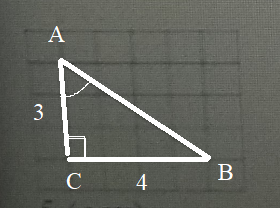
Достраиваем угол до прямоугольного треугольника АВС
∠ C=90 °
Катет АС=3 клеточкам
катет BC= 4 клеточкам
1 клеточка =1 см
АС=3 см
ВС=4 см
По теореме ПИфагора
AB^2=AC^2+BC^2=3^2+4^2=9+16=25
AB=5 cм
Косинус острого угла прямоугольного треугольника равен
отношению прилежащего катета к гипотенузе:
[m]cos angle A= frac{AC}{AB}=frac{3}{5}=0,6[/m]
О т в е т .0,6
Написать комментарий
юра фролов
Ученик
(58),
закрыт
8 лет назад
” />
Дополнен 8 лет назад

Тесты_математика
Гений
(51456)
8 лет назад
cos=–3/(3^2+4^2)=-3/5
Тоня БайгишиеваУченик (231)
8 лет назад
А почему –3 делят?
Тесты_математика
Гений
(51456)
потому что cos -это отношение прилежащего катета к гипотенузе а гипотенузу ищешь по теореме Пифагора я уже забыла про эту задачу так давно было он скоро должен быть уже на голосовании на ЛУЧШИЙ ОТВЕТ
Лариса Козина
Мудрец
(13373)
8 лет назад
Давай выполним дополнительные построения
1)продли влево горизонтальную прямую, 2)из верхнего конца наклонной опусти перпендикуляр
Слева у тебя получился прямоугольный треугольник
Теперь обозначим углы, прилежащие к горизонтальной прямой. Острый угол в треугольнике обозначим а, справа тупой угол обозначим в
Решение: cosb=cos(180-a)=-cosa
Гипотенуза в треугольнике по т Пифагора равна5
-cosa=-35=-0,6
