Свойства ромба:
1. Ромб – частный случай параллелограмма
2. Противоположные стороны – параллельны
3. Все четыре стороны – равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы косинуса углов через диагональ и сторону:
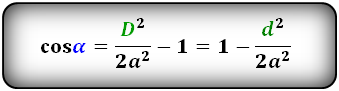
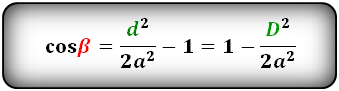
Формулы синуса углов через диагонали :
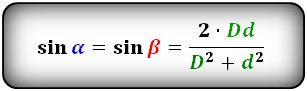
Формулы синуса углов через площадь S и сторону :
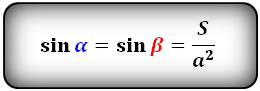
Формулы тангенса половинных углов через диагонали
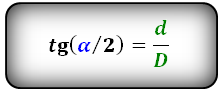
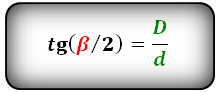
Формулы соотношения острого и тупого углов:

Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
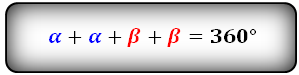
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 25 ноября 2011
-
Обновлено: 13 августа 2021
диагонали ромба равны 12 и 16 найдите косинус его тупого угла
Светило науки – 6 ответов – 0 раз оказано помощи
АВСD – ромб, АС = 12 и ВD = 16
диагонали пересекаются в точке М
Тогда АМ = СМ = 6
ВМ = DM =8,
a (сторона ромба )=10
в треугольнике АВD
BD^2 = AB^2 +AD^2 – 2AB*AD*cos(BAD)
256=100+100-200cosBAD
cosBAD=-7/25

Светило науки – 33 ответа – 3274 помощи
вроде бы так сначала найдем допустим сторону вс=корень открывается (64+36)=100 корень из 100=10 найдем косинус угла всн =6/10 так как угол с состоит из углов всн и dсн то 2*0,6=1,2
Ромб. Формулы, признаки и свойства ромба
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 – 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 – 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 – d22
d2 = √4a2 – d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Ромб – геометрическая фигура, представляющая собой отдельную разновидность параллелограмма. Все
имеющееся стороны равны между собой. Геометрическая фигура представляет собой отдельную
разновидность параллелограмма. Все имеющееся стороны равны между собой. Чтобы исключить риски
недопонимания, а также освоить принципы расчетов, рекомендуется ознакомиться с некоторыми
особенностями подробней.
- Острый угол ромба через длинную диагональ и сторону
- Острый угол ромба через короткую диагональ и сторону
- Тупой угол ромба через длинную диагональ и сторону
- Тупой угол ромба через короткую диагональ и сторону
- Острый угол ромба через диагонали
- Угол ромба через площадь и сторону
- Острый угол ромба через радиус вписанной окружности в ромб
и площадь ромба - Острый угол ромба через высоту и сторону
- Половинный угол ромба через высоту и диагональ
- Половинный острый угол ромба через диагонали
- Половинный тупой угол ромба через диагонали
Острый угол ромба через длинную диагональ и сторону
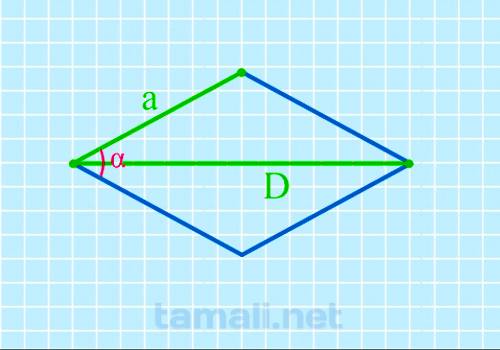
Для проведения расчетов используется формула:
cos α = D² / 2a² — 1
где D — длинная диагональ, a — сторона.
Цифр после
запятой:
Результат в:
Пример. Предположим, что длинная диагональ 25 мм, сторона – 15 мм. Отталкиваясь от
полученных сведений, результат получается следующим: cos α = 25² / 2 х 15² — 1 = 67.11º
Тупой угол ромба через длинную диагональ и сторону
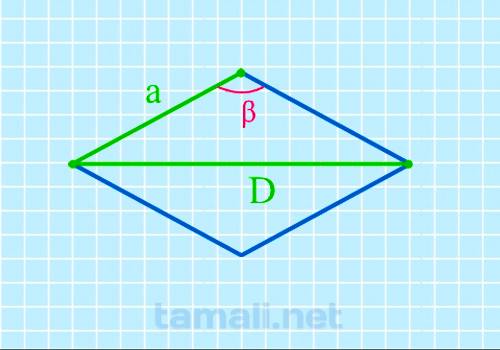
Имея достоверные данные о значение длинной диагонали (D) и стороне (a), порядок вычисления не
предполагает под собой каких-либо сложностей с определением. Для этого в геометрии предлагается
воспользоваться следующей формулой:
cos β = D² / 2a² — 1
Цифр после
запятой:
Результат в:
Пример. Предположим, D = 60 мм, a = 90 мм. Исходя из полученных сведений, расчет по
имеющейся формуле имеет вид: cos β = 60² / 2 х 90² — 1. В таком
случае cos β = 141.05. При условии, что D>a, решение не представляется возможным.
Острый угол ромба через короткую диагональ и сторону
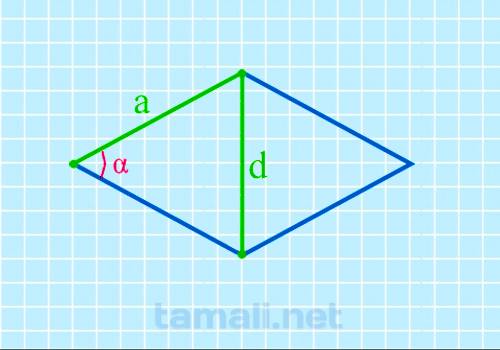
Для проведения интересующегося расчета требуется знать данные о короткой диагонали (d) и стороне (a).
При условии наличия используемая формула имеет следующий вид:
cos α = 1 – d² / 2a²
где d — короткая диагональ, a — сторона.
Цифр после
запятой:
Результат в:
Пример. Из представленной формулы следует, что инициировать получение интересующих
данных не вызывает сложностей. Чтобы удостовериться в этом, достаточно рассмотреть пример. Допустим,
что d = 40 мм, a = 25 мм. В таком случае определение результата осуществляется следующим образом:
cos α = 1 – 40² / 2 х 25².
Используя калькулятор, становится известно,
что cos α = 106.26. Подтвердить подлинность результата можно в режиме онлайн через
специализированный сервис вычислений.
Острый угол ромба через диагонали
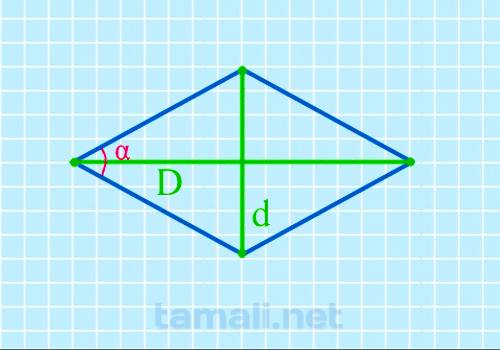
Представленный параметр расчета по праву считается одним из наиболее сложных. Чтобы исключить риски
допущения ошибок и недопонимания, рекомендуется ответственно подходить к организации вычислений.
Чтобы узнать информацию, чему равняется sin α, достаточно воспользоваться следующей формулой:
sin α = (2 · Dd)/ (D² + d²)
где D является длинной диагональю, d — короткой.
Цифр после
запятой:
Результат в:
Во время определения sin α оптимальным решением станет использование стандартных математических
правил. Они предполагают первичное умножение, после чего деление. Суммирование осуществляется на
завершающем этапе определения значения.
Пример. Предположим, D = 85 мм, d = 15 мм. Имеющиеся значения требуется подставить в
формулу. В итоге получается: sin α = (2 · 85)/85² + 15². Используя
автоматизированный калькулятор для геометрии, получается, что sin α = 20.01
Тупой угол ромба через короткую диагональ и сторону
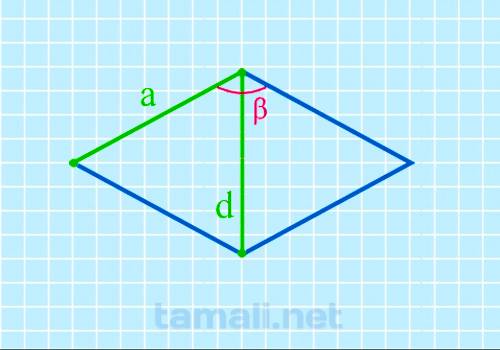
Порядок вычисления предполагает использование соответствующей формулы. Чтобы инициировать расчет
требуется знать точные данные относительно короткой диагонали (d) и стороне (a). В таком случае
расчет проходит следующим образом:
cos β = 1 — d² / 2a²
где d — короткая диагональ, a — сторона ромба.
Цифр после
запятой:
Результат в:
Пример. Предположим, что d = 27 мм, a = 65 мм. Используя имеющуюся формулу,
вычисление проходит по следующей процедуре: cos β = 1 — 27²/2х65².
Используя стандартные принципы
вычисления либо специализированный онлайн калькулятор, cos β = 23.98. Чтобы гарантировать
достоверность вычислений настоятельно рекомендуется выполнять проверку полученных данных несколькими
способами.
Острый угол ромба через радиус вписанной окружности в ромб и площадь ромба
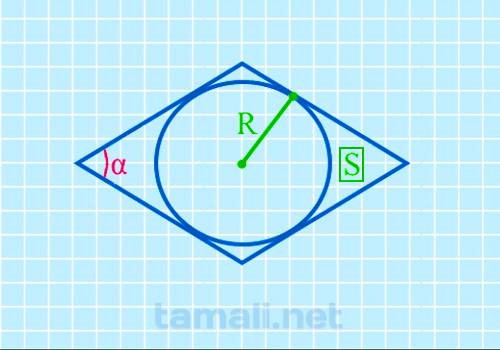
Принципы определения интересующей величины предполагают необходимость использования следующей
формулы:
sin(α) = 4R²/S
где R – радиус, S – заявленная площадь геометрической фигуры.
Цифр после
запятой:
Результат в:
Пример. Предположим, что радиус составляет 2 см, заявленная площадь 20 мм² .
Подставив имеющиеся значения в формулу, имеем следующий вид: sin(α) = 4 х 2²/20 = 53º.
Угол ромба через площадь и сторону
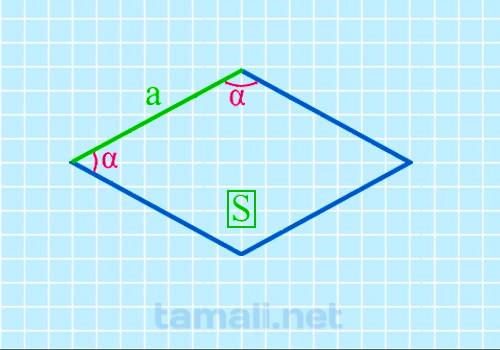
Представленный метод часто используется, чтобы узнать интересующий параметр. Главное условие –
наличие известных величин из формулы, которая имеет следующий вид:
sin(α) = S/a²
где S является площадью ромба, a — стороной.
Цифр после
запятой:
Результат в:
Рассмотрим порядок определения неизвестной величины на конкретном примере. Допустим, что S = 65 мм² ,
a – 12 мм. В таком случае, получается: sin(α) = 65/12³ = 26,83º.
Острый угол ромба через высоту и сторону
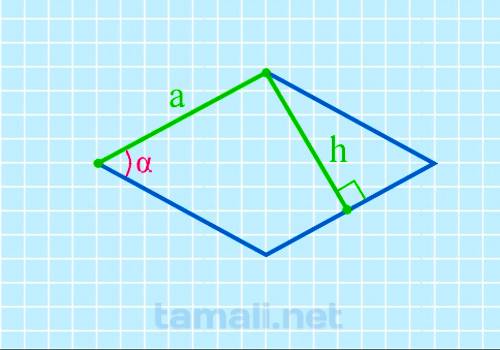
Для определения синуса предполагается использование следующей несложной формулы:
sin(α) = h / a
где h – заявленные показатели высоты, a — сторона.
Цифр после
запятой:
Результат в:
Пример. Допустим, что высота составляет 9, сторона – 15. Следовательно, вычисления
осуществляются следующим образом: sin(α) = 9/15 = 36.86 градусов.
Половинный угол ромба через высоту и диагональ
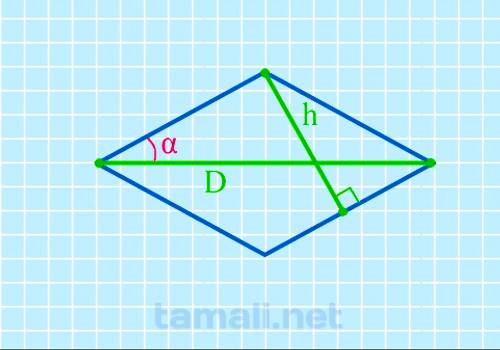
Чтобы отыскать интересующий синус, требуется воспользоваться следующим правилом определения
величины:
sin( α/2 ) = h/D
где h – имеющаяся высота, D – заявленная длина диагонали.
Цифр после
запятой:
Результат в:
Пример. Высота 43, диагональ 76. Следовательно, sin( α/2 ) = 43/76 = 34.4.
Половинный тупой угол ромба через диагонали
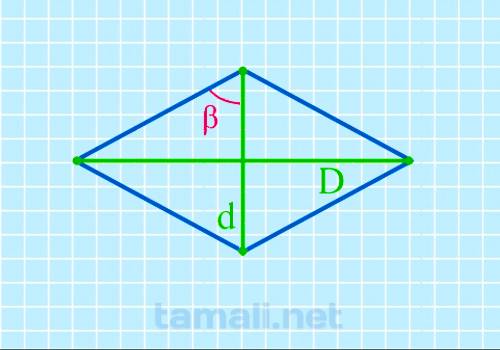
Использование рассматриваемого метода не предполагает под собой существенных сложностей. Достаточно
воспользоваться специально разработанной формулой, которая имеет следующий вид:
tg( β/2 ) = D / d
где D выступает длинной диагональю, d — короткой.
Цифр после
запятой:
Результат в:
Пример. Достаточно подставить для вычисления имеющиеся данные, чтобы в конечном
итоге получить искомый результат. К примеру, D = 80 мм, d = 35 мм. Используя стандартные принципы
вычисления получается: tg( β/2 ) = 80/35 = 66.37
Половинный острый угол ромба через диагонали
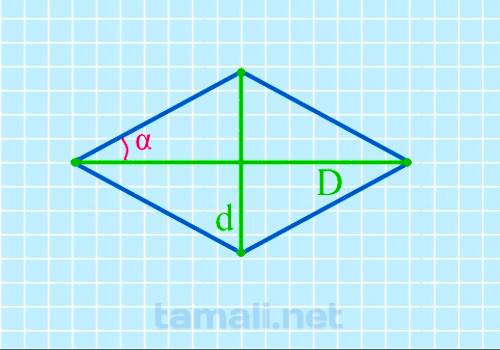
Проведение расчетов с помощью представленной методики требует наличия всех переменных, среди которых
короткая и длинная диагонали. Если все необходимые параметры известны, вычисление осуществляется по
представленной формуле:
tg( α/2 ) = d / D
где D,d – заявленная длина диагоналей.
Цифр после
запятой:
Результат в:
Пример. Предположим, что D = 15 мм, d = 50 мм. Подставим имеющие значения в формулу,
имеем вид: tg( α/2 ) = 50 /15 С помощью несложных подсчетов получается, что tg( α/2 ) = 73.3
градуса.
Ромб представляет собой параллелограмм, который имеем равные стороны. При наличии исключительно
прямых углов – квадрат.
Дополнительно выделяют следующие признаки:
- имеющиеся диагонали ромба перпендикулярны;
- диагонали ромба выступают биссектрисами его углов;
- сумма квадратов всех диагоналей приравнивается к квадраты стороны, которая умножается на 4.
Чтобы параллелограмм считался ромбом, крайне важно соблюдение одного из нескольких условий, к которым
принято относить:
- все имеющиеся стороны геометрической фигуры равны между собой;
- диагонали пересекаются исключительно под прямым углом;
- диагонали геометрической фигуры выступают биссектрисами углов.
Бенедикт
13 января, 17:47
-

Силуян
13 января, 18:09
0
Напротив большего угла лежит большая диагональ значит АС=16 лежит напротив тупого угла В.
найдем сторону ромба по теореме Пифагора = sqrt 36 + 64 = sqrt 100 = 10
cos угла ОВС (половина АВС) = 6/10=0,6
так как диагонали ромба являются биссектрисами его углов значит тупой угол АВС=0,6*2=1,2
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Диагонали ромба равны 12 и 16. Найти cos его тупого угла …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по геометрии
