Решение:
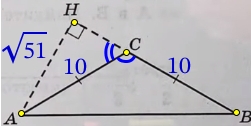
В прямоугольном ΔАНС по теореме Пифагора найдём катет НС:
HC=sqrt{AC^{2}-AH^{2}}=sqrt{10^{2}-(sqrt{51})^{2}}=sqrt{100-51}=sqrt{49}=7
Косинусы смежных углов равны по модулю, противоположны по знаку:
cos∠ACB = –cos∠ACH
Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Найдём cos∠ACH:
cosangle ACH=frac{HC}{AC}=frac{7}{10}=0,7
Найдём косинус искомого угла АСВ:
cos∠ACB = –cos∠ACH = –0,7
Ответ: –0,7.
Решение:
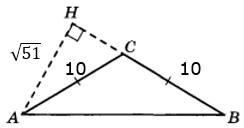
Чтобы решить эту задачу просто необходимо знать вот такую клевую информацию:
синусы смежных углов равны, а косинусы, тангенсы и котангенсы смежных углов противоположны.
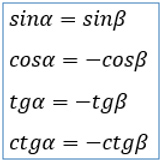
Более подробно о синусах, коминусах, тангенсах и котангенсах можно прочитать тут.
Таким образом нужно найти косинус угла HCA и просто подрисовать минус перед числом, которое получится.
Косинус – это отношение прилежащего катета НС к гипотенузе АН.
Катет НС неизвестен, находим его по теореме Пифагора:
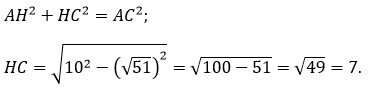
Далее находим косинус угла HCA:
![]()
И автоматически находим cosACB: он равен -0,7.
Ответ: -0,7.
#936
Перейти к содержанию
На чтение 1 мин. Просмотров 8.2k.
В тупоугольном треугольнике ABC известно, что AC=BC=10, высота AH равна √51. Найдите косинус угла ACB.
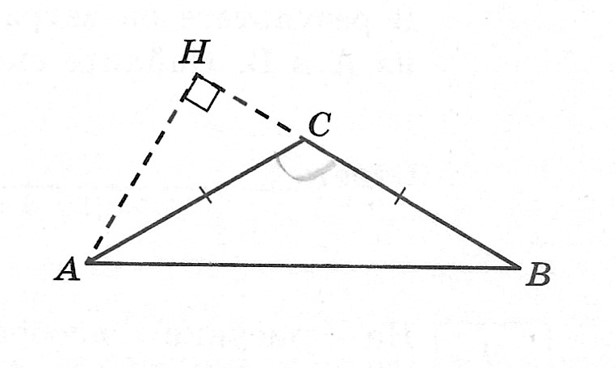
Решение:
Косинус угла ACB удобнее всего находить по теореме косинусов:
![]() .
.
Нам известны AC и CB, нужно лишь найти AB.
Для того, чтобы найти сторону AB из прямоугольного треугольника AHB, найдем сначала сторону HB.
![]() ,
,
CB известна по условию задачи. Найдем из треугольника AHC сторону HC по теореме Пифагора:
![]()
![]()
![]() .
.
Тогда ![]()
Теперь найдем AB: ![]()
Подставим значение AB в формулу теоремы косинуса: ![]() ;
;
![]() ;
;
![]()
![]()
![]()
Ответ: -0,7
( 11 оценок, среднее 4.09 из 5 )
Теорема косинусов и синусов

О чем эта статья:
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 – 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
BC 2 = a 2 = (b cos α – c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α – 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) – 2bc cos α + c 2
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 – a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 – a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 – a 2
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 – (b × cos α) 2
- h 2 = a 2 – (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 – (b × cos α) 2 = a 2 – (c – b × cos α) 2
- a 2 = b 2 + c 2 – 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 – 2ac × cos β;
- c 2 = a 2 + b 2 – 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 – 2bc cos α
b 2 = c 2 + a 2 – 2ca cos β
c 2 = a 2 + b 2 – 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
-
Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
- Если c 2 2 + b 2 , то ∠C — острый.
Теорема косинусов. Доказательство теоремы косинусов.
Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.
Теорема косинусов:
 Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:
Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:
Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Следствие из теоремы косинусов.
- Теорема косинусов используется для определения cos угла треугольника:

h 2 = a 2 – (c – b cos α) 2 (2)
Приравниваем правые части уравнений (1) и (2):
b 2 – (b cos α) 2 = a 2 – (c – b cos α) 2
a 2 = b 2 + c 2 – 2bc cos α.
Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определить стороны b и c:
Решение №2303 В тупоугольном треугольнике ABC известно, что AC = BC = 10, высота AH равна √51.
В тупоугольном треугольнике ABC известно, что AC = BC = 10, высота AH равна √51. Найдите косинус угла ACB.
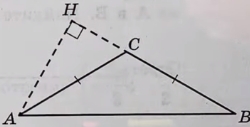
Источник: Ященко ЕГЭ 2022 (36 вар)

В прямоугольном ΔАНС по теореме Пифагора найдём катет НС:
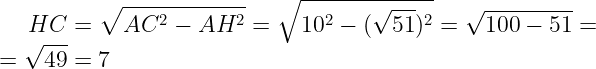 Косинусы смежных углов равны по модулю, противоположны по знаку:
Косинусы смежных углов равны по модулю, противоположны по знаку:
cos ∠ACB = –cos ∠ACH
Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Найдём cos∠ACH:
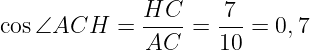
Найдём косинус искомого угла АСВ:
cos∠ACB = –cos∠ACH = –0,7
[spoiler title=”источники:”]
http://www.calc.ru/Teorema-Kosinusov-Dokazatelstvo-Teoremy-Kosinusov.html
[/spoiler]
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается
.
Угол обозначается соответствующей греческой буквой
.

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим.Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
:
Мы получили основное тригонометрическое тождество.
- Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике угол
равен
,
. Найдите
.
Задача решается за четыре секунды.
Поскольку ,
.
2. В треугольнике угол
равен
,
,
. Найдите
.

Имеем:
Отсюда
Найдем по теореме Пифагора.
Задача решена.
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
