lfrenea205
Вопрос по геометрии:
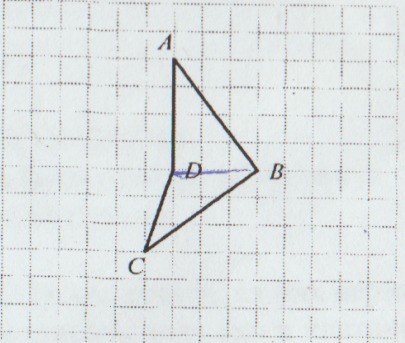
На рисунке изображен четырехугольник ABCD. По рисунку найдите косинус угла DAB.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
ereala513
Рассмотрим ∆ DAB.
Он прямоугольный (т.к. ∠ADB = 90°).
Считая по клеточкам, находим длины катетов.
AD = 4, DB = 3. По теореме Пифагора находим гипотенузу:
АВ = √3² + 4² = √9 + 16 = √25 = 5.
cosDAB = AD/AB = 4/4 = 0,8 (косинус – это отношение прилежащего катета к гипотерузе).
Ответ: 0,8.
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
![]()
3
1 ответ:
![]()
0
0
Рассмотрим ∆ DAB.
Он прямоугольный (т.к. ∠ADB = 90°).
Считая по клеточкам, находим длины катетов.
AD = 4, DB = 3. По теореме Пифагора находим гипотенузу:
АВ = √3² + 4² = √9 + 16 = √25 = 5.
cosDAB = AD/AB = 4/4 = 0,8 (косинус – это отношение прилежащего катета к гипотерузе).
Ответ: 0,8.
Читайте также
![]()
Сумма углов выпуклово n-угольника по теореме равна 180°(n-2)
Угла у четырехугольника 4 значит n=4 следовательно сумма углов нашего четырехугольника равна (4-2)*180°=2*180°=360°
110+70+35+155=180+190=370°≠360°⇒такой четырехугольник не существует
Ответ: не существует
![]()
1 основание 6 см, средняя линия 9, 2 основание 12
![]()
<span>Квадрат АВСД, АС=ВД=10*корень2,
АД=ВС=СД=АД=корень(АС в квадрате/2)=корень(200/2)=10, О – пересечение
диагоналей, ОК-перпендикуляр к плоскости АВСД, точка М на АВ, Н-на ВС, Р
на СД, Т на АД, точки лежат на серединах сторон квадрата,
МК=НК=РК=ТК=13, проводим ОМ параллельнуюАД, треугольник ОМК
прямоугольный, ОМ=1/2АД=10/2=5, ОК=корень(МК в квадрате-ОМ в
квадрате)=корень(169-25)=12-расстояния</span>
![]()
Однозначно НЕЛЬЗЯ!!!!!!!!!!
![]()
Периметр : (диагональ + диагональ)
Косинус угла. Таблица косинусов.
Косинус угла через градусы, минуты и секунды
Косинус угла через десятичную запись угла
Как найти угол зная косинус этого угла
У косинуса есть обратная тригонометрическая функция – arccos(y)=x
cos(arccos(y))=y
Пример cos(60°) = 1/2; arccos(1/2) = 60°
Рассчитать арккосинус
Определение косинуса
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
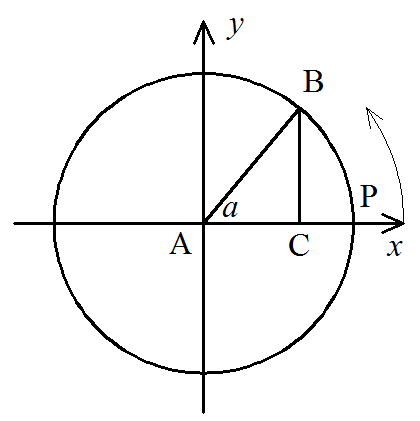
cos(α) = AC/AB
cos(-α) = cos(α)
cos(α ± 2π) = cos(α)
Таблица косинусов в радианах
cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0.7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
Таблица Брадиса косинусы
| cos(0) = 1 | cos(120) = -0.5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
| cos(9) = 0.9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0.6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0.2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
| cos(20) = 0.9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0.01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
| cos(38) = 0.7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0.9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
| cos(49) = 0.656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0.4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0.9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0.6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
| cos(77) = 0.2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0.9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0.8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
| cos(88) = 0.0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0.8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0.9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
| cos(106) = -0.2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0.6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0.9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
| cos(117) = -0.4539904997 | cos(237) = -0.544639035 | cos(357) = 0.9986295348 |
| cos(118) = -0.4694715628 | cos(238) = -0.5299192642 | cos(358) = 0.999390827 |
| cos(119) = -0.4848096202 | cos(239) = -0.5150380749 | cos(359) = 0.9998476952 |
Похожие калькуляторы
Теорема косинусов и синусов

О чем эта статья:
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 – 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
BC 2 = a 2 = (b cos α – c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α – 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) – 2bc cos α + c 2
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 – a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 – a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 – a 2
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 – (b × cos α) 2
- h 2 = a 2 – (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 – (b × cos α) 2 = a 2 – (c – b × cos α) 2
- a 2 = b 2 + c 2 – 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 – 2ac × cos β;
- c 2 = a 2 + b 2 – 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 – 2bc cos α
b 2 = c 2 + a 2 – 2ca cos β
c 2 = a 2 + b 2 – 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
-
Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
- Если c 2 2 + b 2 , то ∠C — острый.
Косинус b решение треугольников
Ключевые слова: треугольник, угол, косинус, прямоугольный треугольник, теорема косинусов, теорема синусов, решение треугольников
Решение прямоугольных треугольников
Рассмотрим прямоугольный треугольник ABC. В нем
Решение произвольных треугольников
Для решения произвольных треугольников существует теорема косинусов и теорема синусов.
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Теорема синусов позволяет по двум сторонам и углу, лежащему против одной из них (или по стороне и двум углам) вычислить остальные элементы треугольника.
См. также:
Площадь треугольника, Прямоугольный треугольник, Равнобедренный треугольник, Равносторонний треугольник
Решение треугольников
Корзина


Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,

 A =
A = 
 CAB,
CAB, 
 B =
B = 
 ABC,
ABC, 
 C =
C = 
 BCA − углы, противолежащие сторонам a, b, c соответственно.
BCA − углы, противолежащие сторонам a, b, c соответственно.


Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле “Текст с картинки”. Нажмите “Решить”.
Теоретический урок для решения задач по теме “Решение треугольников”. Бесплатное обучение.
Содержание данной онлайн страницы электронного справочника по предмету математики для школьников:
- – задачи 76 – 77 представлены с примерами решений и ответами;
- – онлайн задания, как найти решение треугольника через синус и косинус угла, рассматриваются в тестах 78 – 81;
- – решения, как найти угол, сторону треугольника, объясняются на данном уроке в контрольных работах 82 – 85.
Задача 76.

 Дано:
Дано:
стороны треугольника a=10, b=7
Угол 
 A = 60°
A = 60°
Решить треугольник: Угол по сторонам треугольника 
 B,
B, 
 C, сторону c
C, сторону c

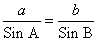 , получаем выражение
, получаем выражение
Sin B = 
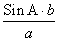 =
= 
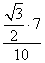 =
= 
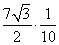 =
= 
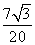 ≈ 0,6062
≈ 0,6062
Используя Sin B ≈ 0,6062, находим из тригонометрической таблицы (“Четырехзначные математические таблицы” Владимира Модестовича Брадиса)

 B = 37°19’
B = 37°19’
Тогда 
 C = 180° – (60° + 37°19’) = 82°41’
C = 180° – (60° + 37°19’) = 82°41’
Используя теорему синусов

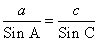 , получаем равенство
, получаем равенство

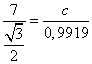

 с=
с= 
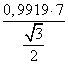 ≈ 11
≈ 11
Ответ: 
 B = 37°19’;
B = 37°19’; 
 C = 82°41’; c ≈ 11
C = 82°41’; c ≈ 11
Задача 77.
Треугольник ΔABC, стороны треугольника



 C = 54°
C = 54°
Найти: Угол по сторонам треугольника 
 A,
A, 
 B, сторону c
B, сторону c
Т.к. a=b=6,3, то треугольник ΔABC – равнобедренный.
Тогда 
 A =
A = 
 B = (180° – 54°): 2 = 63°
B = (180° – 54°): 2 = 63°
Используя теорему синусов

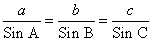 , получаем равенство
, получаем равенство

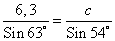

 с =
с = 
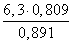 =
= 
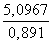 ≈ 5,7
≈ 5,7
Ответ: 
 A =
A = 
 B = 63°; с ≈ 5,7
B = 63°; с ≈ 5,7
Решение треугольников через синус и косинус угла
Задача 78.

 A = 60°
A = 60°



 B = 40°
B = 40°
Найти: угол треугольника 
 C, стороны a,b
C, стороны a,b

 C = 180° – (40° + 60°) = 80°
C = 180° – (40° + 60°) = 80°
Используя теорему синусов

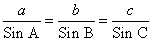 , получаем выражение
, получаем выражение

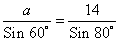

 a =
a = 
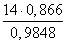 ≈ 12
≈ 12

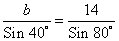

 b =
b = 
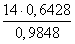 ≈ 9
≈ 9
Ответ: 
 C = 80°; a ≈ 12; b ≈ 9
C = 80°; a ≈ 12; b ≈ 9
Задача 79.

 Дано:
Дано:
Найти: углы треугольника 
 A,
A, 
 B,
B, 
 C по сторонам
C по сторонам

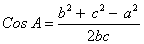 , находим косинус угла B
, находим косинус угла B
Cos B = 
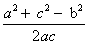 =
= 
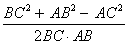 =
= 
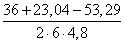 =
= 
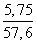 ≈ 0,0998263
≈ 0,0998263
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим значение угла B

 B = 84°16’
B = 84°16’
Используя формулу теоремы косинусов, находим косинус угла C
Cos C = 
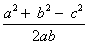 =
= 
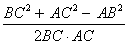 =
=
= 
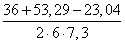 ≈ 0,7562785
≈ 0,7562785
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим значение угла C

 C = 40°52’
C = 40°52’
Тогда угол A равен 
 A =180° – (40°52’ + 84°16’) = 54°52’
A =180° – (40°52’ + 84°16’) = 54°52’
Ответ: 
 A = 54°52’ ;
A = 54°52’ ; 
 C = 40°52’ ;
C = 40°52’ ; 
 B = 84°16’
B = 84°16’
Задача 80.

 A = 30°
A = 30°

 C = 75°
C = 75°
Найти: угол 
 B, стороны треугольника a,c
B, стороны треугольника a,c

 B = 180° – (30° + 75°) = 75°
B = 180° – (30° + 75°) = 75°
Т.к. два угла в треугольнике равны 
 B =
B = 
 C = 75°, тогда треугольник ΔABC – равнобедренный.
C = 75°, тогда треугольник ΔABC – равнобедренный.
Значит, две стороны равны AC=AB=b=c=4,5
Используя теорему синусов

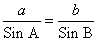 ,
,
находим сторону BC=a



 a =
a = 
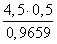 ≈ 2,3
≈ 2,3
Ответ: 
 B = 75°; a ≈ 2,3 ; c = 4,5
B = 75°; a ≈ 2,3 ; c = 4,5
Задача 81.
Треугольник ΔABC, длины трех его сторон
Найти: является ли треугольник тупоугольным, прямоугольным, остроугольным
1) Т.к. b=c=4, то треугольник ΔABC – равнобедренный, и, значит, остроугольный.

 2) Используя формулу теоремы косинусов
2) Используя формулу теоремы косинусов

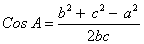 , находим косинус угла A
, находим косинус угла A
Cos A = 
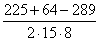 =
= 
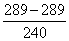 =0
=0
Тогда угол A равен 
 A = 90°. Следовательно, треугольник ΔABC – прямоугольный.
A = 90°. Следовательно, треугольник ΔABC – прямоугольный.
3) Используя формулу теоремы косинусов

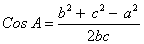 , находим косинус угла B
, находим косинус угла B
Cos B = 
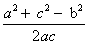 =
= 
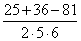 = –
= – 
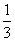
 Дано:
Дано:
Треугольник ΔABC, два угла и сторона

 A = 45°
A = 45°

 C = 30°
C = 30°
Найти: длину всех сторон треугольника ΔABC = ?
Зная размер двух углов в треугольнике ΔABC, находим третий угол 
 B = 180° – (30° + 45°) = 105°
B = 180° – (30° + 45°) = 105°
Найдем угол 
 DAB и рассмотрим ΔADC
DAB и рассмотрим ΔADC

 DAB = 180° – (90° + 45 + 30°) = 15°
DAB = 180° – (90° + 45 + 30°) = 15°

 DAC = 15° + 45° = 60°
DAC = 15° + 45° = 60°
Используя теорему синусов

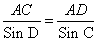 , находим сторону AC
, находим сторону AC

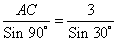


AC = (3 • 1) • 2 = 6 (м)
Используя теорему синусов

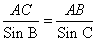 , находим сторону AB
, находим сторону AB

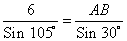


AB = 
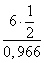 ≈ 3 (м)
≈ 3 (м)
Используя теорему синусов

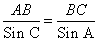 , находим сторону BC
, находим сторону BC

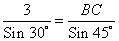

 BC =
BC = 
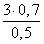 ≈ 4 (м)
≈ 4 (м)
Ответ: AB ≈ 3 м, AC = 6 м, BC ≈ 4 м.

 Задача 83.
Задача 83.
Три стороны a = 14, b = 18,
все углы треугольника ΔABC = ?
Т.к. против большего угла лежит большая сторона, то используя формулу теоремы косинусов
Cos C = 
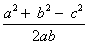 , находим косинус угла C
, находим косинус угла C
Cos C = 
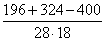 =
= 
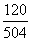 ≈ 0,24
≈ 0,24
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим приближенное значение угла C

 C ≈ 76°07’
C ≈ 76°07’
Используя формулу теоремы косинусов
Cos B = 
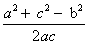 , находим косинус угла B
, находим косинус угла B
Cos B = 
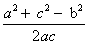 =
= 
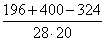 =
= 
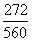 ≈ 0,4857
≈ 0,4857
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим приближенное значение угла B

 B ≈ 60,941 ≈ 60°57’
B ≈ 60,941 ≈ 60°57’
Следовательно, 
 A = 180° – (76°13’ + 60°57’) ≈ 42°56’
A = 180° – (76°13’ + 60°57’) ≈ 42°56’
Ответ: 
 A ≈ 42°56’ ;
A ≈ 42°56’ ; 
 B ≈ 60°57’ ;
B ≈ 60°57’ ; 
 C ≈ 76°07’
C ≈ 76°07’


Задача 84.
Треугольник ΔEKP, сторона и два угла

 P = 40°
P = 40°

 K = 25°
K = 25°
Найти: сторону треугольника PK = ?
Используя теорему синусов

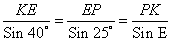 , находим сторону PK
, находим сторону PK

 E = 180° – (40° + 25°) =115°
E = 180° – (40° + 25°) =115°
Sin 115° = Sin (180° – 65°) = Sin 65°
Тогда 
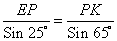



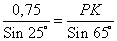



 PK =
PK = 
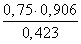 ≈ 1,61
≈ 1,61
Задача 85.
Треугольник ΔABC, две стороны и угол

 A = 50°
A = 50°
Найти: решить треугольник – определить значение стороны и двух углов
(a, 
 B,
B, 
 C ) = ?
C ) = ?
Используя формулу теоремы косинусов

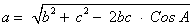 , получаем
, получаем
a = 
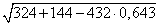 =
= 
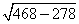 ≈ 13,8
≈ 13,8
Используя формулу теоремы косинусов
Cos C = 
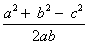 , находим косинус угла C
, находим косинус угла C
Cos C = 
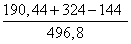 =
= 
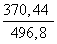 ≈ 0,7457
≈ 0,7457
Используя тригонометрические таблицы (“Четырехзначные математические таблицы” В. М. Брадиса), находим приближенное значение угла C

 C ≈ 41°47’
C ≈ 41°47’
Следовательно, 
 B = 180° – (50° + 41°47’) ≈ 88°13’
B = 180° – (50° + 41°47’) ≈ 88°13’
Ответ: a ≈ 13,8 ; 
 B ≈ 88°13’ ;
B ≈ 88°13’ ; 
 C ≈ 41°47’
C ≈ 41°47’
[spoiler title=”источники:”]
http://uztest.ru/abstracts/?idabstract=75
http://www.petrovskov.ru/uchebniki/geometriya-9/reshenie-treugolnikov.html
[/spoiler]
В данной публикации мы рассмотрим, что такое угол меду двумя векторами, и приведем формулу, с помощью которой можно найти его косинус. Также разберем пример решения задачи по этой теме.
- Нахождение угла между векторами
- Пример задачи
Нахождение угла между векторами
Угол между двумя векторами, берущими начало в одной и той же точке – это наименьший угол, на который можно повернуть один из данных векторов вокруг своей начальной точки до положения, при котором он будет сонаправлен со вторым вектором.

Косинус угла между двумя векторами равняется скалярному произведению векторов, разделенному на произведение длин (модулей) этих векторов.
Для расчета косинуса угла используется формула ниже:

Пример задачи
Найдем угол между векторами a = {4; 3} и b = {12; 5}.
Решение
1. Для начала рассчитаем их скалярное произведение:
a · b = 4 · 12 + 3 · 5 = 48 + 15 = 63.
2. Теперь найдем длины (модули) заданных векторов:
![]()
![]()
3. Применим формулу для нахождения косинуса угла:
![]()
4. Следовательно, угол приблизительно равняется 14,26° (arccos 0,9692).
