Как найти косинус угла если известны стороны

Как найти косинус угла если известны стороны

В статье про прямоугольный треугольник посмотрели задачи связанные с синусами и косинусами из 1 части ОГЭ. Так что обязательно заглядывай.

Получается, что решить прямоугольный треугольник (найти все стороны и острые углы) можно довольно просто, зная всего лишь два элемента прямоугольного треугольника :две стороны (по теореме Пифагора) или сторону и острый угол (из определений синуса, косинуса, тангенса).

Но решить треугольник (найти все стороны и углы ) можно и произвольный, зная три элемента: три стороны, две стороны и угол, или два угла и сторону.

Для первых двух случаев в решении пользуются теоремой косинусов (вполне возможно эта тема вас поджидает уже на следующей неделе в школе, а может уже и была):

в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.

Теорема косинусов в 1 части ОГЭ
  • Если известны три стороны треугольника можно найти косинусы всех углов
  • Если известны две стороны и угол между ними треугольника, то можно найти третью сторону.

В этом случае полезно пользоваться таблицей значений косинусов некоторых углов :

Теорема косинусов в 1 части ОГЭ

Рассмотрим решение задачи №16 из сборника Ященко (36 вариантов) на теорему косинусов :

Теорема косинусов в 1 части ОГЭ

Изобразим треугольник АВС и найдем в нем противолежащую сторону для угла АВС.

Теорема косинусов в 1 части ОГЭ

Из рисунка видно, что противолежащая сторона – это сторона АС.

Для стороны АС записываем теорему косинусов:

Теорема косинусов в 1 части ОГЭ

Подставим значения всех сторон:

Теорема косинусов в 1 части ОГЭ

Переносим все “свободные” числа (меняя знак) в левую часть равенства и считаем:

Теорема косинусов в 1 части ОГЭ

Находим косинус угла АВС, как неизвестный множитель:

Теорема косинусов в 1 части ОГЭ

Записываем ответ:

Теорема косинусов в 1 части ОГЭ

Если вы знаете того, кто готовится к ОГЭ, не забудьте поделиться с ним этой информацией. Всегда пригодится.

Продолжение следует…

Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

(✿◠‿◠)

Теорема косинусов в 1 части ОГЭ
Источник

Стандартные обозначения

Стандартные обозначения углов и сторон треугольника

Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора на произвольные плоские треугольники.

Формулировка[править | править код]

Для плоского треугольника со сторонами a,b,c и углом alpha , противолежащим стороне a,
справедливо соотношение:

{displaystyle a^{2}=b^{2}+c^{2}-2cdot bcdot ccdot cos alpha .}

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними[1]

Доказательства[править | править код]

Классическое доказательство

Theorem of cosin.svg

Рассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует:

AD=bcos alpha ,

откуда

DB=c-bcos alpha .

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

h^{2}=b^{2}-(bcos alpha )^{2}qquad qquad qquad (1)
h^{2}=a^{2}-(c-bcos alpha )^{2}qquad qquad (2)

Приравниваем правые части уравнений (1) и (2) и:

b^{2}-(bcos alpha )^{2}=a^{2}-(c-bcos alpha )^{2}

или

a^{2}=b^{2}+c^{2}-2bccos alpha .

Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.

Выражения для сторон b и c:

b^{2}=a^{2}+c^{2}-2accos beta
c^{2}=a^{2}+b^{2}-2abcos gamma .

Доказательство через координаты

Одним из доказательств является доказательство её в координатной плоскости.

Внесём в координатную плоскость произвольный треугольник ABC так, чтобы точка А совпала с началом координат, а прямая АВ лежала на прямой ОХ. Введём обозначения AB=c, AC=b, CB=a, a угол CAB=α(пока будем считать что α≠90°).
Тогда точка A имеет координаты (0;0), точка B(c;0). Через функцию sin и cos, а также сторону АС=b выведем координаты точки С. С(b×cosα;b×sinα).
Координаты точки С остаются неизменными при тупом и остром угле α.
Зная координаты С и B, а также зная, что CB=a, найдя длину отрезка, мы можем составить равенство:
a^{2}=(bcos {a}-c)^{2}+b^{2}sin ^{2}{a}
a^{2}=b^{2}cos ^{2}{a}-2bccos {a}+c^{2}+b^{2}sin ^{2}{a}
a^{2}=b^{2}(cos ^{2}{a}+sin ^{2}{a})+c^{2}-2bccos {a}
Так как
cos ^{2}{a}+sin ^{2}{a}=1 (основное тригонометрическое тождество), то
a^{2}=b^{2}+c^{2}-2bccos {a}
Теорема доказана.
Для прямого угла α, теорема также работает cos90°=0 и a²=b²+с² – известная всем теорема Пифагора. Но так как в основе координатного метода лежит теорема Пифагора, то доказательство её через теорему косинусов не совсем правильно.

Доказательство через векторы

Ниже подразумеваются операции над векторами, а не длинами отрезков
{displaystyle AC=AB+BC=>BC=AC-AB=>BC^{2}=AC^{2}+AB^{2}-2cdot ACcdot AB}

Так как скалярное произведение векторов равно произведению их модулей (длин) на косинус угла между ними, последнее выражение можно переписать:
{displaystyle a^{2}=b^{2}+c^{2}-2cdot bcdot ccdot cos alpha }
где a, b, c — длины соответствующих векторов

Следствия[править | править код]

  • Теорема косинусов может быть использована для нахождения косинуса угла треугольника
    cos {alpha }={frac {b^{2}+c^{2}-a^{2}}{2bc}}
В частности,
  • Теорема косинусов может быть записана также в следующем виде[2]:
a^{2}=(b+c)^{2}-4cdot bcdot ccdot cos ^{2}(alpha /2),
a^{2}=(b-c)^{2}+4cdot bcdot ccdot sin ^{2}(alpha /2).

Доказательство

Последние две формулы мгновенно следуют из основной формулы теоремы косинусов (см. в рамке выше), если в правой её части воспользоваться формулами разложения квадрата суммы (для второй формулы – квадрата разности) двух членов на квадратный трехчлен, являющийся полным квадратом. Для получения окончательного результата (двух формул выше) в правой части надо еще воспользоваться известными тригонометрическими формулами:

1+cos alpha =2cdot cos ^{2}(alpha /2),
1-cos alpha =2cdot sin ^{2}(alpha /2).

Кстати, вторая формула формально не содержит косинусов, но её все равно именуют теоремой косинусов.

Для других углов[править | править код]

Теорема косинусов для двух других углов имеет вид:

{displaystyle c^{2} =a^{2}+b^{2}-2abcos gamma }
{displaystyle b^{2} =a^{2}+c^{2}-2accos beta }

Из этих и из основной формулы могут быть выражены углы:

{displaystyle alpha =arccos left({frac {b^{2}+c^{2}-a^{2}}{2bc}}right)}
{displaystyle beta =arccos left({frac {a^{2}+c^{2}-b^{2}}{2ac}}right)}
{displaystyle gamma =arccos left({frac {a^{2}+b^{2}-c^{2}}{2ab}}right)}

История[править | править код]

Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.

Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях ал-Баттани.[3]:105
Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» по имени ал-Баттани.

В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии.
В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.

Вариации и обобщения[править | править код]

  • Теоремы косинусов (сферическая геометрия) или Теорема косинусов для трёхгранного угла.
  • Теоремы косинусов (геометрия Лобачевского)
  • Тождество параллелограмма. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон (см. также Теорема Птолемея):
    AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}.

Для евклидовых нормированных пространств[править | править код]

Пусть в евклидовом пространстве E задана норма, ассоциированная со скалярным произведением, то есть leftVert {vec {a}}rightVert ={sqrt {({vec {a}},{vec {a}})}}. Тогда теорема косинусов формулируется следующим образом:

Теорема.
leftVert {vec {a}}-{vec {b}}rightVert ^{2}=leftVert {vec {a}}rightVert ^{2}+leftVert {vec {b}}rightVert ^{2}-2({vec {a}},{vec {b}})

Для четырёхугольников[править | править код]

Возводя в квадрат тождество {overline {AD}}={overline {AB}}+{overline {BC}}+{overline {CD}} можно получить утверждение, иногда называемое теоремой косинусов для четырёхугольников:

d^{2}=a^{2}+b^{2}+c^{2}-2abcos angle B-2accos omega -2bccos angle C, где omega  — угол между прямыми AB и CD.

Или иначе:

d^{2}=a^{2}+b^{2}+c^{2}-2abcos angle B+2accos(angle A+angle D)-2bccos angle C
Формула справедлива и для тетраэдра, под w подразумевается угол между скрещивающимися ребрами.
С помощью неё можно найти косинус угла между скрещивающимися ребрами a и c зная все ребра тетраэдра:
{displaystyle cos w=(b^{2}+d^{2}-e^{2}-f^{2})/2ac}
Где b и d, e и f пары скрещивающихся ребер тетраэдра.

Косвенный аналог для четырёхугольника[править | править код]

Соотношение Бретшнайдера — соотношение в четырёхугольнике, косвенный аналог теоремы косинусов:

Между сторонами a, b, c, d и противоположными углами {displaystyle alpha ,gamma } и диагоналями e, f простого (несамопересекающегося) четырёхугольника выполняется соотношение:

{displaystyle e^{2}f^{2}=a^{2}c^{2}+b^{2}d^{2}-2abcdcos(alpha +gamma )}
  • Если четырёхугольник вырождается в треугольник, и одна вершина попадает на сторону, то получается теорема Стюарта.
  • Теорема косинусов для треугольника является частным случаем соотношения Бретшнайдера, если в качестве четвёртой вершины выбрать центр описанной окружности треугольника.

Симплексы[править | править код]

{displaystyle S_{i}S_{j}cos angle A={frac {(-1)^{(n-1+i+j)}}{2^{n-1}((n-1)!)^{2}}}{begin{vmatrix}0&1&1&1&dots &1\1&0&d_{12}^{2}&d_{13}^{2}&dots &d_{1(n+1)}^{2}\1&d_{21}^{2}&0&d_{23}^{2}&dots &d_{2(n+1)}^{2}\1&d_{31}^{2}&d_{32}^{2}&0&dots &d_{3(n+1)}^{2}\vdots &vdots &vdots &vdots &ddots &vdots \1&d_{(n+1)1}^{2}&d_{(n+1)2}^{2}&d_{(n+1)3}^{2}&dots &0\end{vmatrix}}}

при этом мы должны зачеркнуть строку и столбец, где находится d_{ij} или d_{ji}.

A — угол между гранями S_{i} и S_{j}, S_{i} -грань, находящаяся против вершины i,d_{ij}– расстояние между вершинами i и j.

См. также[править | править код]

  • Решение треугольников
  • Скалярное произведение
  • Соотношение Бретшнайдера
  • Теорема косинусов для трёхгранного угла
  • Теорема о проекциях
  • Теорема Пифагора
  • Сферическая теорема косинусов
  • Теорема котангенсов
  • Теорема синусов
  • Теорема тангенсов
  • Тригонометрические тождества
  • Тригонометрические функции

Примечания[править | править код]

  1. ↑ Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 7—9: учеб. для общеобразоват. учреждений — 15-е изд. — М.: Просвещение, 2005. — С. 257. — 384 с.: ил. — ISBN 5-09-014398-6
  2. ↑ 1 2 Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — С. 51. — 832 с.
  3. ↑ Florian Cajori. A History of Mathematics — 5th edition 1991

Литература[править | править код]

  • Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 84—85. — ISBN 5-94057-170-0.
Источник

Как находить косинус в треугольнике

Нередко в геометрических (тригонометрических) задачах требуется найти косинус угла в треугольнике, потому что косинус угла позволяет однозначно определить величину самого угла.

Треугольник АВС

Инструкция

Чтобы найти косинус угла в треугольнике, длины сторон которого известны, можно воспользоваться теоремой косинусов. Согласно этой теореме, квадрат длины стороны произвольного треугольника равняется сумме квадратов двух его других сторон без удвоенного произведения длин этих сторон на косинус угла между ними:

а?=b?+c?-2*b*c*соs?, где:

а, b, с – стороны треугольника (точнее их длины),

? – угол, противоположный стороне а (его величина).

Из приведенного равенства легко находится соs?:

соs?=( b?+c?-а? )/(2*b*c)

Пример 1.

Имеется треугольник со сторонами а, b, с, равными 3, 4, 5 мм, соответственно.

Найти косинус угла, заключенного между большими сторонами.

Решение:

По условию задачи имеем:

а=3,

b=4,

с=5.

Обозначим противоположный стороне а угол через ?, тогда, согласно выведенной выше формуле, имеем:

соs?=(b?+c?-а? )/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40=32/40=0,8

Ответ: 0,8.

Если треугольник прямоугольный, то для нахождения косинуса угла достаточно знать длины всего двух любых сторон (косинус прямого угла равен 0).

Пусть имеется прямоугольный треугольник со сторонами а, b, с, где с – гипотенуза.

Рассмотрим все варианты:

Пример 2.

Найти соs?, если известны длины сторон а и b (катеты треугольника)

Воспользуемся дополнительно теоремой Пифагора:

c?=b?+а?,

с=v(b?+а?)

соs?=(b?+c?-а? )/(2*b*c)=(b?+b?+а?-а?)/(2*b*v(b?+а?))=(2*b?)/(2*b*v(b?+а?))=b/v(b?+а?)

Чтобы проверить правильность полученной формулы, подставим в нее значения из примера 1, т.е.

а=3,

b=4.

Проделав элементарные вычисления, получаем:

соs?=0,8.

Аналогично находится косинус в прямоугольном треугольнике в остальных случаях:

Пример 3.

Известны а и с (гипотенуза и противолежащий катет), найти соs?

b?=с?-а?,

b=v(c?-а?)

соs?=(b?+c?-а? )/(2*b*c)=(с?-а?+с?-а?)/(2*с*v(с?-а?))=(2*с?-2*а?)/(2*с*v(с?-а?))=v(с?-а?)/с.

Подставляя значения а=3 и с=5 из первого примера, получаем:

соs?=0,8.

Пример 4.

Известны b и с (гипотенуза и прилежащий катет).

Найти соs?

Произведя аналогичные (показанные в примерах 2 и 3 преобразования), получим, что в этом случае косинус в треугольнике вычисляется по очень простой формуле:

соs?=b/с.

Простота выведенной формулы объясняется элементарно: фактически, прилежащий к углу ? катет является проекцией гипотенузы, поэтому его длина равна длине гипотенузы, умноженной на соs?.

Подставляя значения b=4 и с=5 из первого примера, получим:

соs?=0,8

Значит, все наши формулы верны.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Учебник

Геометрия, 9 класс

Теорема косинусов

Теорема косинусов    

Если в треугольнике даны   две стороны и угол между ними, то такой треугольник один, единственный.   Т.е. любой другой треугольник с такими данными будет в точности равен ему, по   2-му признаку равенства   треугольников.    Ну, раз единственный и неповторимый, то его третья   сторона   должна   быть однозначно   определяема.

_____________________________________________________________________________________

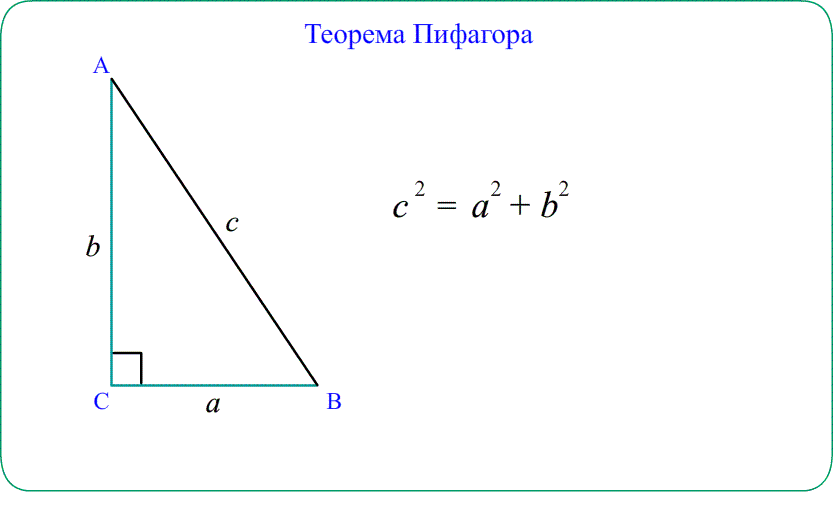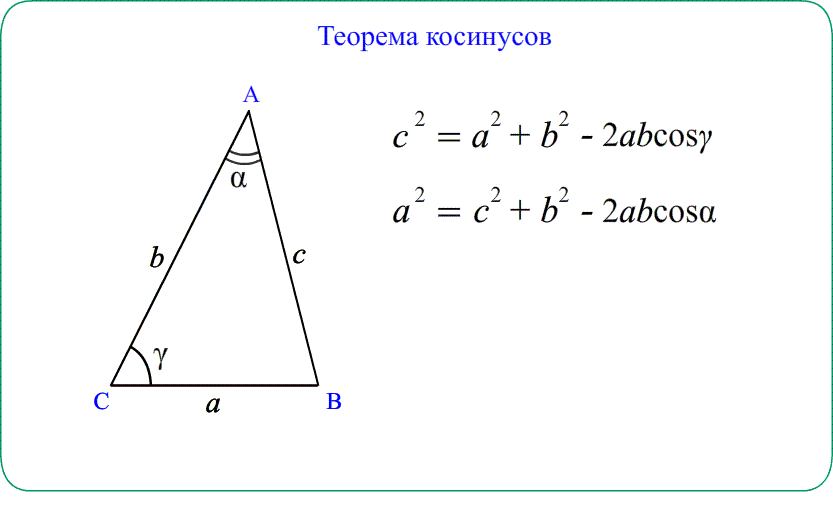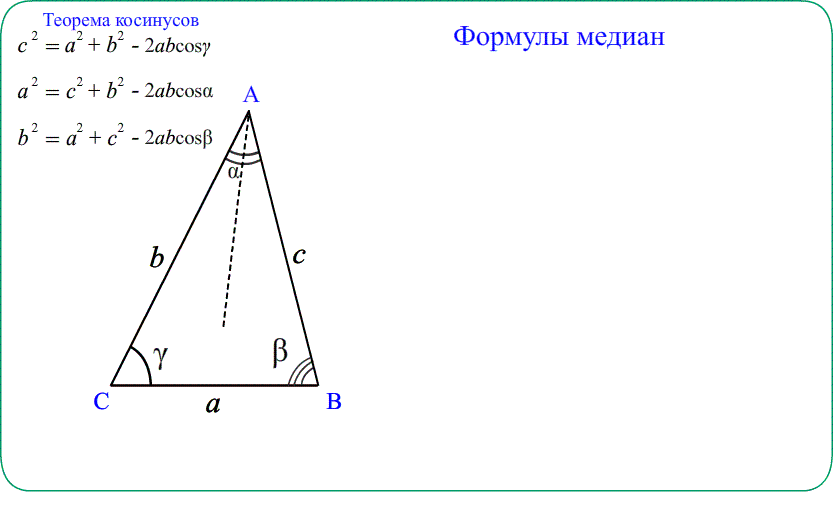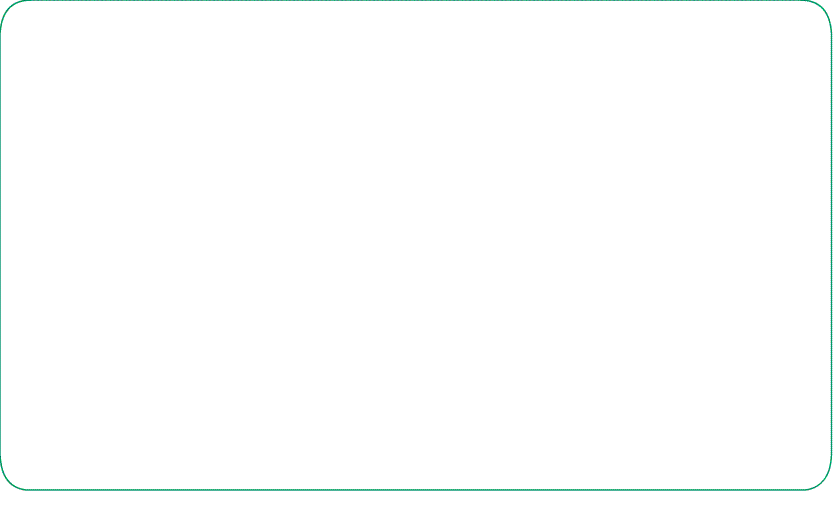
Теорема косинусов    Квадрат стороны треугольника      равен     сумме квадратов двух
   
других сторон минус     удвоенное произведение этих сторон   на    косинус угла между ними.
      
$AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos ACB$

_____________________________________________________________________________________

Факты:

  • Теорема косинусов позволяет найти косинус любого угла по трем известным сторонам, а значит,   и сам угол.
  • Если из трех сторон и одного   угла известны три величины, то четвертое неизвестное можно   всегда вычислить.
  • Теорема косинусов   дает возможность   вычислять   медианы треугольника,   применяя теорему к малым треугольникам.
  • Для прямоугольного треугольника теорема косинусов    “упрощается”   до теоремы Пифагора       $AB^2=AC^2+BC^2$.

       

А если угол тупой? Что означает тригонометрия больших углов?

$cos130=-cos50$,    $sin115=sin65$ ,   $tg135=-tg45$.    

Связь   тригонометрии   тупых   углов    $90 < alpha < 180$    с    тригонометрией    острых     выражается   формулами:      
     $sinalpha=sinleft(180-alpharight)$           $cosalpha=-cosleft(180-alpharight)$        $tgalpha=-tgleft(180-alpharight)$        $ctgalpha=-ctgleft(180-alpharight)$

Если $b^2+c^2-a^2>0$, то $alpha$ – острый;     если $b^2+c^2-a^2=0$, то   $alpha$ – прямой;    если   $b^2+c^2-a^2<0$ , то угол $alpha$ – тупой.

Расчет треугольников по теореме косинусов    

Задача 1:        В треугольнике   $ABC$   сторона   $AC$ равна   $7sqrt{3}$ см,   сторона   $BC$ равна $1$ см ,   угол $C$ = $150^o$ .          Найти   длину стороны   $AB$.

  • Решение:          Применим   теорему косинусов      $AB^2=left(7sqrt{3}right)^2+1-14sqrt{3}cos150$ .
  • Тупой     угол    в $150^o$      выразим     через     острый :       $cos150=cosleft(180-30right)=-cos30=-frac{sqrt{3}}{2}$.         $Rightarrow$      
  • $AB^2=147+1-28sqrt{3}left(-frac{sqrt{3}}{2}right)$      ,         $AB^2= 148 + 21 = 169$           $Rightarrow$                             Ответ:     $AB = 13$

Задача 2:        В треугольнике   $ABC$   сторона   $AC$ равна   $17$ см,   сторона   $BC$ равна $14$ см ,   угол $ACB$ = $60^o$ .
                          Найти   длину третьей стороны   .

  • Решение:          Из   теоремы косинусов для угла    $angle ACB$ :     $Rightarrow$             $AB^2=17^2+14^2-2cdot17cdot14cdotcos60$                 $Rightarrow$   
  • квадрат стороны      $AB^2= 289+196-238 = 247$           $Rightarrow$           Ответ:     $AB = sqrt{247}$

Задача 3:        В   $bigtriangleup ABC$   известны   $AC=3$   , $BC=5$ см,    $AB=6$ .
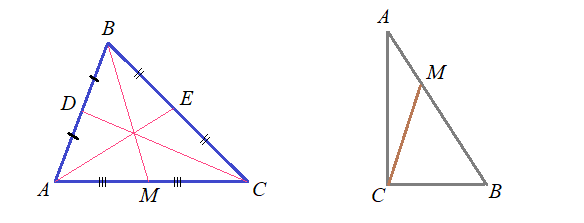
     Найти   косинус   угла   $C$   и медиану    $BM$   .

  • Решение:          Из   теоремы   косинусов    для стороны    $AB$ выразим косинус требуемого угла $ACB$:   
  • $cos ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}=frac{9+25-36}{30}=-frac{1}{15}$   .      Отрицательное значение косинуса говорит о том, что это тупой   угол $>90^o$
  • Для нахождения    медианы   $ВМ$    распишем     еще раз теорему косинусов, но уже для треугольника     $ВМС$   от угла $С$:
  • $BM^2=BC^2+MC^2-2cdot BCcdot MCcdotcos C$    учтем,   что     медиана   делит сторону   пополам    $MC=frac{AC}{2}=1,5$
  • Подставим     $BM^2=25+2,25-2cdot5cdot1.5cdotleft(-frac{1}{15}right)=27,25+1=28,25$,     получим      $BM=sqrt{28,25}=0,5sqrt{113}$    
  • Ответ:          $cos ACB=-frac{1}{15}$        ,    $BM=0,5sqrt{113}$     .

Задача 4:        В прямоугольном   $bigtriangleup ABC$   известны   $AB=9$ , $BC=3$ см ;    $M$ делит   $AB$ :      $frac{AM}{MB}=frac{1}{2}$.
                          Найти    $CM$   .

  • Решение:         По свойству     аддитивности    отрезка     $AM + MB = 9$ ,   по условию      $frac{AM}{MB}=frac{1}{2}$      $Rightarrow$    $AM = 3$ ,    $MB = 6$
  • Из прямоугольного   $bigtriangleup ABC$    по определению косинуса угла:       $cos B=frac{BC}{AB}=frac{3}{9}=frac{1}{3}$    .
  • Из     $bigtriangleup CMB$       по теореме косинусов найдем   $CM$ :    $CM^2=CB^2+MB^2-2cdot CBcdot MBcdotcos B$       , подставим   числа
  • $CM^2=3^2+6^2-2cdot3cdot6cdotfrac{1}{3}=33$      $Rightarrow$    требуемый   отрезок     $CM=sqrt{33}$      .             Ответ:          $CM=sqrt{33}$

Задача 5:        Одна из сторон треугольника   больше   другой   на   $8$    см, а угол между ними $120^o$ .
                          Найдите периметр треугольника, если длина третьей стороны    $28$ см   .

  • Решение:     Метод введения неизвестного:    Обозначим   одну   из   сторон   треугольника как   $x$ ,
  • выразим нужные величины через х и составим уравнение:    величина   другой стороны будет равна    $x+8$ см.
  • По теореме косинусов:    $28^2=x^2+left(x+8right)^2-2xcdotleft(x+8right)cdotcos120$ ,   где      $cos120=cosleft(180-60right)=-cosleft(60right)=-0,5$,
  • Итак, составили уравнение    $784=x^2+x^2+16x+64-2xleft(x+8right)left(-0,5right)$               $Rightarrow$          $3x^2+24x+720=0$
  • решим   квадратное уравнение : один корень отрицательный – не нужен ,    другой     $x=frac{-24+96}{6}=12$        
  • Периметр    $P=12+left(12+8right)+28=60$.             Ответ:           $60$.

Задача 6:       В     $bigtriangleup ABC$   известны   стороны    $a=15$ , $b=18$,   $c=25$ .          Найти:   углы   $α$,    $β$,    $γ$   (приближённо) .

  • Решение:         Углы    $α$    и    $β$     найдём по теореме косинусов для соответствующих углов.            
  • $cosalpha=frac{b^2+c^2-a^2}{2bc}$ , вычисляем      $cosalpha=frac{18^2+25^2-15^2}{2cdot18cdot25}approx0,8$   ,   привлекаем калькулятор: $alphaapprox36,4^o$    ;
  • $cosbeta=frac{a^2+c^2-b^2}{2ac}$ , вычисляем      $cosbeta=frac{15^2+25^2-18^2}{2cdot15cdot25}approx0,7$   ,   …. калькулятор: $betaapprox45,3^o$       .
  • Найдём   $γ$    по теореме о 180 = сумма углов:    $gamma=180-left(alpha+betaright)$    и    $gammaapprox180-left(36,4+45,3right)approx98,3$   .
  • Ответ:                 $alphaapprox36,4^o$     ,      $betaapprox45,3^o$       ,      $gammaapprox98,3$

          

Задача 7:         В     $bigtriangleup ABC$        $AB=c=3$ м,      $AC = b = 6$ м.   ,    $alpha=60$   .       Найти:   сторону    $a = BC$   ,     углы     $β$,    $γ$    .

  • Решение:           Треугольник   задан    двумя   сторонами   и   углом между ними,    следовательно,   он задан полностью.               
  • По   теореме   косинусов      $a^2=b^2+c^2-2bccdotcosalpha$          найдём сторону     $a$:      
  • $a^2=6^2+3^2-2cdot6cdot3cdotcos60=36+9-36cdotfrac{1}{2}=27$          $Rightarrow$     $a=3sqrt{3}$ .
  • По теореме   косинусов   найдем и    угол    $β$ :     $cosbeta=frac{a^2+c^2-b^2}{2ac}$      ,     $cosbeta=frac{27+9-36}{18sqrt{3}}=0$     $Rightarrow$      $β=90$ .
  • Значит $bigtriangleup ABC$   –    прямоугольный   ,      тогда угол    $γ=90-α$     .          Ответ:    $a=3sqrt{3}$   ,    $β = 90$     ,    $γ=30$   .

Задача 8:         Стороны треугольника равны   $11$   ,    $12$    и     $13$ .    Найти биссектрису, проведенную к стороне, равной 12.

  • дано: $AB=11$   ,     $BC=12$    ,   $AC=13$               Найти биссектрису      $AK=?$ .
  • Решение:     Найдем косинус угла из теоремы косинусов :     $AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos angle ACB$                     
  • Выразим косинус       $cos angle ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}$ ,    $cos angle ACB=frac{13^2+12^2-11^2}{2cdot 13cdot 12}=frac{19}{39}$
  • Найдем отрезки   $BK$ ,   $KC$    на которые биссектриса делит сторону … по теореме биссектрис         $frac{BK}{KC}=frac{AB}{AC}$
  • Система уравнений: $frac{BK}{KC}=frac{11}{13}$ и аддитивность $BK+KC=BC=12$. Получаем    $BK=5,5$ ,    $BK=6,5$
  • Теперь, для нахождения биссектрисы   $AK$   еще раз     используем теорему косинусов для треугольника     $bigtriangleup AKC$
  • $AK^2=AC^2+KC^2-2cdot ACcdot KCcdotcos angle ACB$    подставим значения    $AK^2=13^2+6,5^2-2cdot 13cdot 6,5cdot frac{11}{13}=frac{429}{4}$.
  • Ответ:         $AK=frac{sqrt429}{2}$.

Задача 9:         Стороны треугольника равны   $11$   ,    $12$    и     $13$ .    Найти медиану, проведенную к большей стороне.

  • Решение:         Воспользуемся формулой для длины медианы:        $m_c=frac{1}{2}sqrt{2a^2+2b^2-c^2}$                     
  • Подставим   значения   $m_c=frac{1}{2}sqrt{2cdot11^2+2cdot12^2-13^2}=frac{1}{2}sqrt{242+288-169}=frac{1}{2}sqrt{361}=frac{19}{2}=9,5$     Ответ:       $m_c=9,5$

Задача 10:         В треугольнике     $ABC$     $AB=11$   ,     $AC=23$    ,    медиана      $AK=10$ .           Найти     $BC$ .

  • Решение:          Воспользуемся   формулой   для   длины    медианы      и   подставим    в   неё   данные   из условия:                  
  • $AK=frac{1}{2}sqrt{2cdot11^2+2cdot23^2-BC}$        $Rightarrow$      $100=frac{1}{4}left(242+1058-BC^2right)$         $Rightarrow$   $BC^2=900$          Ответ:           $BC=30$        .    

Упражнения:

Источник

Для нахождения элементов в произвольном треугольнике используется теорема синусов или теорема косинусов.

4cepure.JPG

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов: 

asinA=bsinB=csinC

(в решении задачи одновременно пишутся две части, они образуют пропорцию).

Теорема синусов используется для вычисления:

  • неизвестных сторон треугольника, если даны два угла и одна сторона;

  • неизвестных углов треугольника, если даны две стороны и один прилежащий угол.

Так как один из углов треугольника может быть тупым, значение синуса тупого угла находится по формуле приведения

sin180°−α=sinα

.

Наиболее часто используемые тупые углы:

sin120°=sin180°−60°=sin60°=32;sin150°=sin180°−30°=sin30°=12;sin135°=sin180°−45°=sin45°=22.

Радиус описанной окружности

Треуг2.jpg

asinA=bsinB=csinC=2R

, где (R) — радиус описанной окружности.

Выразив радиус, получаем

R=a2sinA

, или

R=b2sinB

, или

R=c2sinC

.

Для вычисления элементов прямоугольного треугольника достаточно (2) данных величин (две стороны или сторона и угол).

Для вычисления элементов произвольного треугольника необходимо хотя бы (3) данных величины.

4cepure.JPG

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Также теорема исполняется для любой стороны треугольника:

Теорема косинусов используется для вычисления:

  • неизвестной стороны треугольника, если даны две стороны и угол между ними;

  • вычисления косинуса неизвестного угла треугольника, если даны все стороны треугольника.

Значение косинуса тупого угла находится по формуле приведения

cos180°−α=−cosα

.

Наиболее часто используемые тупые углы:

cos120°=cos180°−60°=−cos60°=−12;cos150°=cos180°−30°=−cos30°=−32;cos135°=cos180°−45°=−cos45°=−22. 

Если необходимо найти приблизительное значение синуса или косинуса другого угла или вычислить угол по найденному синусу или косинусу, то используется таблица или калькулятор.

Источники:

Рис. 1-3. Треугольник, окружность, © ЯКласс.

Источник

Добавить комментарий