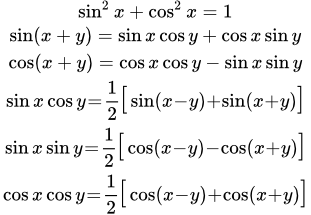Как найти косинус угла физика

2.1. Теорема Пифагора

Прямоугольный треугольник — треугольник, в котором один из углов прямой (то есть равен 90°). Сторона, противолежащая прямому углу, называется гипотенузой. Стороны, образующие прямой угол, называются катетами (см. рис.).

Для любого прямоугольного треугольника справедлива теорема Пифагора:

Гипотенузу можно найти по формуле:

Катет можно найти по формуле:

2.2 Как найти и из прямоугольного треугольника?

Рассмотрим прямоугольный треугольник с катетами a и b и гипотенузой c. Обозначим через α угол, лежащий напротив катета a (см. рис.).

Тогда, катет a — противолежащий катет для угла α (лежит напротив угла); катет b — прилежащий катет (непосредственно образует угол).

Синус угла α — отношение противолежащего катета к гипотенузе:

Косинус угла α — отношение прилежащего катета к гипотенузе:

Тангенсом угла α — отношение противолежащего катета к прилежащему:

2.3 Как найти проекции вектора, если известен его модуль и направление?

1) Опускаем перпендикуляры на ось Ox и ось Oy;

2) Проекции равны:

3) Правило знаков.

Пусть даны вектор и ось Ox. Из начала и конца вектора опустим перпендикуляры на ось Ox. Пусть A и B — основания этих перпендикуляров (см. рис.).

Проекция вектора на ось Ox (Oy) равна длине отрезка AB, взятой со знаком плюс, если угол φ между вектором и осью Ox (Oy) является острым, и взятой соответственно со знаком минус, если φ тупой (или развернутый). Если угол φ прямой, то

То есть:

Получаем:

2.4 Как найти проекции вектора, если известны координаты начала и конца вектора?

Пусть и ) — координаты начала и конца вектора соответственно. Тогда проекции

2.5 Как найти модуль вектора, если известны его проекции на оси?

Если известны проекции вектора и на оси координат, то модуль вектора легко найти по формуле:

2.6 Как найти модуль вектора, если известны координаты конца и начала вектора?

Пусть и  — координаты начала и конца вектора соответственно. Тогда модуль вектора находится по формуле:

2.7 Теорема косинусов.

Для треугольника со сторонами a, b и c, углом α справедлива теорема:

2.8 Как сложить вектора, направленные вдоль одной прямой?

Пусть даны вектора и имеющие одинаковое направление. Для нахождения вектора помещаем начало вектора в конец вектора и соединяем начало вектора с концом вектора (см. рис.).

Из рисунка видно, что модуль вектора равен:

2.9 Как вычитать вектора, направленные вдоль одной прямой?

Пусть даны вектора и имеющие одинаковое направление. Для нахождения вектора помещаем начало вектора  в конец вектора и соединяем начало вектора с концом вектора (см. рис.). Вектор  — это вектор, длина которого равна длине вектора , но имеет противоположное направление.

Из рисунка видно, что модуль вектора равен:

2.10 Как сложить вектора, направленные под прямым углом друг к другу?

Пусть даны вектора и имеющие одинаковое направление. Для нахождения вектора помещаем начало вектора в конец вектора и соединяем начало вектора с концом вектора (см. рис.).

Из рисунка видно, что модуль вектора равен:

2.11 Как вычитать вектора, направленные под прямым углом друг к другу?

Пусть даны вектора и имеющие одинаковое направление. Для нахождения вектора помещаем начало вектора в конец вектора и соединяем начало вектора с концом вектора (см. рис.). Вектор  — это вектор, длина которого равна длине вектора но имеет противоположное направление.

Из рисунка видно, что модуль вектора равен:

2.12 Как сложить вектора, направленные под углом α друг к другу?

Пусть даны вектора и , имеющие одинаковое направление. Для нахождения вектора помещаем начало вектора в конец вектора и соединяем начало вектора с концом вектора (см. рис.).

По теореме косинусов, получаем:

2.13 Как вычитать вектора, направленные под прямым углом друг к другу?

Пусть даны вектора и имеющие одинаковое направление. Для нахождения вектора помещаем начало вектора в конец вектора и соединяем начало вектора с концом вектора (см. рис.). Вектор  — это вектор, длина которого равна длине вектора , но имеет противоположное направление.

По теореме косинусов, получаем:

2.14 Площадь треугольника.

Площадь любого треугольника можно найти по формуле

2.15 Площадь прямоугольника.

Площадь любого прямоугольника можно найти по формуле

2.16 Площадь трапеции.

Площадь любой трапеции можно найти по формуле

2.17 Длина окружности.

Длина окружности равна:

2.18 Длина дуги.

Длина дуги:

Тригонометрия в физике.

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Многие из нас хотя бы раз в жизни задавались вопросом: зачем нужна тригонометрия? Впервые мы сталкиваемся с данным понятием в 8 классе при изучении  темы «Соотношения между сторонами и углами прямоугольного треугольника». На этом этапе мы узнаем, что такое синус, косинус и тангенс. Перейдя в 9 класс, мы вновь возвращаемся к тригонометрии. Здесь вводится понятие единичная окружность, с помощью которой определяются функции улов. Перейдя же в 10 класс, мы снова сталкиваемся с тригонометрией и понимаем, что она стала посложнее: ввелось понятие радианная мера угла,  появились тригонометрические уравнения и неравенства, а также стали изучаться  графики тригонометрических функций. Таким образом,  изучая весь этот материал, становится интересно посмотреть на практическую сторону тригонометрии. Для начала нужно сказать о том, что тригонометрия – это раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Слово тригонометрия состоит из двух греческих слов: «trigwnon» – «треугольник» и «metrew» – «измерять», означает – «измерение треугольников». Именно эта задача – «измерение треугольников» или «решение треугольников», определение всех элементов треугольника по трем данным, с древнейших времен составила основу практических приложений тригонометрии. Сложно представить, но с этой наукой мы сталкиваемся не только на уроках математики, но и в нашей повседневной жизни. Многие из нас даже не подозревают, что тригонометрия нашла широкое применение в таких науках как физика, биология, химия, компьютерная графика, геодезия, океанология. Также большую роль тригонометрия играет в медицине и, на удивление, ее используют даже в музыке при описании звуковых волн.

Актуальность: Данная  тема, бесспорно, является актуальной. Тригонометрия использовалась людьми за много лет до нашей эры, уже тогда без знания этой науки было невозможно построить дом, а астрономам не удавалось провести различные расчеты. Спустя тысячелетия ничего не изменилось, тригонометрия по-прежнему остается одной из самых нужных наук, поэтому ее основы должен знать каждый человек, для того чтобы производить расчеты и иметь представление о самых элементарных функциях, так как тригонометрия заставляет думать логически и концентрирует наше внимание.

Цель: Определение связи  тригонометрии с окружающим миром.

Задачи:

1.Рассмотреть историю возникновения и развития тригонометрии.

2.Показать на примерах практическое применение тригонометрии в физике.

3.Раскрыть на примерах возможности использования тригонометрических функций.

Гипотеза: Большинство физических явлений природы, физиологических процессов, закономерностей в музыке и искусстве можно описать с помощью тригонометрии и тригонометрических функций.

Методы исследования:

1. Теоретический анализ
2. Проведение исследования

Практическая значимость: проект может использоваться в качестве теоретического курса в  качестве дополнения, закрепления уже пройденного материала или на внеурочных занятиях.

1.История возникновения тригонометрии

Зачатки тригонометрии можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.

От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами (введение этих единиц в древнегреческую математику обычно приписывают Гипсиклу, II век до н. э.).

Среди известных вавилонянам теорем была, например, такая: вписанный угол, опирающийся на диаметр круга — прямой. Главным достижением этого периода стало соотношение, позже получившее название теоремы Пифагора. Неизвестно, знали ли общую формулировку теоремы древние египтяне, но прямоугольный «египетский треугольник» со сторонами 3, 4 и 5 был там хорошо известен и широко использовался.

Общее и логически связное изложение тригонометрических соотношений появилось в древнегреческой геометрии. Греческие математики ещё не выделяли тригонометрию как отдельную науку, для них она была частью астрономии. Впервые само слово тригонометрия встречается в 1505 году в заглавии книги немецкого математика Питискуса.

Основным достижением античной тригонометрической теории стало решение в общем виде задачи «решения треугольников», то есть нахождения неизвестных элементов треугольника, исходя из трёх заданных его элементов (из которых хотя бы один является стороной).

В данном случае измерение треугольников следует понимать как решение треугольников, т. е. определение сторон, углов и других элементов треугольника, если даны некоторые из них.

Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.

Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10′ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще.

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

2.Тригонометрические функции

Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении  дифференциальных и функциональных уравнений.

 К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.

 Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OМ и положительным направлением оси Ox равен α.

    Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: 
sinα=y/r. 
Поскольку r=1, то синус равен ординате точки M(x,y).

      Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: 
cosα=x/r 

      Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: 
tanα=y/x,x≠0 

      Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: 
cotα=x/y,y≠0 

      Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): 
secα=r/x=1/x,x≠0 

      Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): 
cscα=r/y=1/y,y≠0 

   В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: 
Синусом угла α называется отношение противолежащего катета к гипотенузе. 
Косинусом угла α называется отношение прилежащего катета к гипотенузе. 
Тангенсом угла α называется противолежащего катета к прилежащему. 
Котангенсом угла α называется прилежащего катета к противолежащему. 
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету. 
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету. 

  График функции синус 
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1 

 График функции косинус 
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1 

График функции тангенс  y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞<tanx<∞ 

График функции котангенс  y=cotx, область определения: x∈R,x≠kπ, область значений: −∞<cotx<∞ 

График функции секанс  y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪[1,∞) 

График функции косеканс  y=cscx, область определения: x∈R,x≠kπ, область значений: cscx∈(−∞,−1]∪[1,∞) 

3.Тригонометрия в физике

В технике и окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения. Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения.

Механические колебания

Механическими колебаниями называют движения тел, повторяющихся точно (или приблизительно) через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или маятник. Возьмем, например, гирю, подвешенную на пружине (см. рис.) и толкнем ее вниз. Гиря начнет колебаться вниз и вверх. Как показывают расчеты, отклонение гири от положения равновесия выражается формулой

 s=  sinwt.

  Здесь v0-скорость, с которой мы толкнули гирю,  w= , где m-масса гири, k – жесткость пружины.

  Если мы сначала оттянем гирю на s0 см, а потом толкнем ее со скоростью v0, то она будет совершать колебания по более сложному закону:

s=Asin(wt+a).

  Расчеты показывают, что амплитуда А этого колебания равна ,а число таково, что tga= . Из-за слагаемого a это колебание отличается от колебания s=Asinwt.

  График колебания (2) получается из графика колебания(1) сдвигом влево

на  . Число a – начальная фаза.

  Колебания маятника

Колебания маятника тоже приближенно происходят по синусоидальному закону. Графическое изображение этой функции, дающее наглядное представление о протекании колебательного процесса во времени удобно рассмотреть с помощью модели маятника программы « Функции и графики»

Если эти колебания малы, то угол отклонения маятника приближенно выражается формулой: ,где l-длина маятника, а j0-начальный угол отклонения. Чем длиннее маятник, тем медленнее он качается. Измеряя период колебания маятника известной длины, можно вычислять ускорение земного тяготения g в различных точках земной поверхности.

Разряд конденсатора.

Не только многие механические колебания происходят по синусоидальному закону. И в электрических цепях возникают синусоидальные колебания. Так в цепи, изображенной в правом верхнем углу модели, заряд на обкладках конденсатора изменяется по закону

 q = CU + (q0 – CU) cos ωt, где С- емкость конденсатора, U –напряжение на источнике тока, L –индуктивность катушки,  – угловая частота колебаний в цепи.

  Благодаря модели конденсатора можно устанавливать параметры колебательного контура и строить, соответствующие графики g(t)и I(t). На графиках  хорошо видно как влияет напряжение на изменение силы тока и заряда конденсатора, при этом видно, что при положительном напряжении заряд также принимает положительные значения. На рисунке показано, что при изменении емкости конденсатора( при изменении индуктивности катушки) и сохранении неизменными остальных параметров меняется период колебаний, т. е. меняется частота колебаний силы тока в цепи и меняется частота заряда конденсатора.

          Баллистическое движение
          Баллистика – раздел механики, изучающий движение тел в поле тяжести Земли.

Пули снаряды и бомбы, так же как и теннисный, и футбольный мячи, и ядро легкоатлета, при полете движутся по баллистической траектории.

Закон баллистического движения в координатной форме: (1)

Уравнение траектории снаряда, или зависимость y(x), можно получить, исключая из уравнений системы время. Для этого из первого уравнения системы найдём:

t = .

Подставляя его во второе уравнение, получаем уравнение траектории снаряда:

y = x tg α – (2).

  Траектория баллистического движения.

Построим баллистическую траекторию (2).

Графиком квадратичной функции, как известно, является парабола. В рассматриваемом случае парабола проходит через начало координат,

так как из (2) следует, что у = 0 при х = 0.

Ветви параболы направлены вниз, так как коэффициент ( – ) при x меньше нуля.

Определим основные параметры баллистического движения: время подъема на максимальную высоту, максимальную высоту, время и дальность полета. Вследствие независимости движений по координатным осям подъем снаряда по вертикали определяется только проекцией начальной скорости на ось Y. В соответствии с формулой: полученной для тела, брошенного вверх с начальной скоростью , время подъема снаряда на максимальную высоту равно:

t = .

Максимальная высота подъема может быть рассчитана по формуле

, если  подставить вместо :

y = .

Как соединить две трубы.

Приведенные примеры могут создать впечатление, что синусоиды встречаются только в связи с колебаниями. Однако это не так. Например, синусоиды используются при соединении двух цилиндрических труб под углом друг к другу. Чтобы соединить две трубы таким образом, надо срезать их наискосок.

Если развернуть срезанную наискосок трубу, то она окажется ограниченной сверху синусоидой. В этом можно убедиться, обернув свечку бумагой, срезав ее наискосок и развернув бумагу. Поэтому, чтобы получить ровный срез трубы, можно сначала обрезать металлический лист сверху по синусоиде и свернуть его в трубу.

 Теория радуги.

Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.

Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:

где n1=1, n2≈1,33 – соответственно показатели преломления воздуха и воды, α – угол падения, а β – угол преломления света.

  Северное сияние

Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.

 Сила, действующая на движущуюся в магнитном поле заряженную частицу называется, силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы

  Задачи по тригонометрии с практическим содержанием.

  Тело веса Р положено на наклонную плоскость с углом наклона a. Тело под действием своего собственного веса прошло ускоренно путь S в t секунд. Определить коэффициент трения k.

  Решение:

Сила давления тела на наклонную плоскость F =kPcosa.

Сила, которая тянет тело вниз равна F=Psina-kPcosa=P(sina-kcosa).(1)

Если тело движется по наклонной плоскости, то ускорение а= .

С другой стороны, ускорение а= = =gF ;следовательно,  .(2)

Из равенств (1) и (2) следует, что g(sina-kcosa)=  .

Отсюда: k= =gtga- .

4.Практическая часть

В качестве исследования, я решила провести измерения пандусов двух учреждения нашего города и выяснить, какой из них больше соответствует нормативным требованиям. Пандус –  (фр. pente douce — пологий скат), также рампа — пологая наклонная площадка, соединяющая две разновысокие горизонтальные поверхности, обычно для обеспечения перемещения колёсных транспортных средств с одной на другую. Среди часто встречающихся применений — обеспечение подъезда инвалидных колясок к расположенному над цоколем здания парадному входу.

Пандус магазина «Монетка» (см. приложение 1)

Измерения показали:

высота =40см=0,4м
        длина=240 см=2,4м

Пандус представляет собой прямоугольный треугольник, следовательно, имея данные измерения, можно рассчитать гипотенузу, обозначим ее за с.

с1= √2,42 +0,42 = 2,43 м
Зная гипотенузу, можно рассчитать синус угла наклона.

Синус- это отношение противолежащего катета к гипотенузе.
= = 0,164
Угол наклона пандуса равен 9°.

Рассмотрим пандус, принадлежащий магазину «Дикси» (см. приложение 2)

Высота = 80 см = 0,8 м

Длина=530 см=5,3 м

Соответственно первому решению, найдем гипотенузу (с)

с2=√5,32 +0,82=5,36 м

Найдем синус:  = =0,149
Угол наклона пандуса равен 8°.
           СНиП 35-01-2001

Требования СНиП (строительные нормы и правила) касательно пандусов для инвалидов содержат следующие пункты:

• Максимальная высота подъемного сооружения (одного марша) не должна превышать 0,8 м. Угол наклона при этом должен быть меньше 8%. Если перепад высоты менее 0,2 м, допустимый уклон составляет 10 %.

Таким образом, оба пандуса соответствуют строительным нормам и правилам. Данный пример также показал, что тригонометрия широко применима в жизни.

Заключение

Подводя итог всему выше сказанному, мы подтверждаем гипотезу, выдвинутую вначале проекта. Действительно, большинство физических явлений природы, закономерностей в архитектуре можно описать с помощью тригонометрии и тригонометрических функций. Сейчас в век инновационных технологий еще сложнее представить жизнь без использования тригонометрии. Как показал пример, даже для установления всем привычных пандусов нужно знать элементарную часть тригонометрии, изучаемую в школе.  На каждом шагу мы сталкиваемся с математикой. Однажды  Советский и российский математик Александр Данилович Александров сказал: «Окружающий нас мир – это мир геометрии» и я полностью с ним согласна.

Список литературы:

1. В.А.Косьянов «Физика 10 класс». Издательство «Дрофа», Москва, 2003 год.
2. Ш.А.Алимов «Алгебра и начала математического анализа». Издательство «Просвещение», Москва, 2017 год.
3. http://ya-znau.ru/znaniya/zn/78
4. Детская энциклопедия «Я познаю мир. Физика». Издательство «АСТ», Москва, 1997 год.
5. https://ru.wikipedia.org/wiki/История_тригонометрии
6. http://bouw.ru/article/uklon-pandusa-dlya-invalidov

Приложение:

1.  

Просмотров работы: 7372

I. Механика

Тестирование онлайн

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Тригонометрия: Таблица значений тригонометрических функций

0 °30 °45 °60 °90 °sin α01 22 23 21cos α13 22 21 20tg α03 313нетctg αнет313 30

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

Синус (sin x) и косинус (cos x) – свойства, графики, формулы

Геометрическое определение синуса и косинуса

Синус ( sin α ) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус ( cos α ) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

Принятые обозначения

Графики функций синус, y = sin x , и косинус, y = cos x

Графики синуса и косинуса смещены по оси x друг относительно друга на :
.

Свойства синуса и косинуса

Периодичность

Функции y = sin x и y = cos x периодичны с периодом 2 π .

Четность

Функция синус – нечетная. Функция косинус – четная.

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице ( n — целое).

В этой статье хочу поделиться своими знаниями по таким понятиям, как коэффициент мощности (известный в народе как косинус фи, или cos φ).

Статья не претендует на википедийность!

Если нужны академические знания, с ними можно ознакомиться в книгах и учебниках, которые выложены для свободного скачивания у меня на блоге, на странице Скачать.

Косинус угла в электротехнике

Итак, что такое косинус фи в электротехнике? Дело в том, что есть такое явление, как сдвиг фаз между током и напряжением. Он происходит по разным причинам, и иногда важно знать о его величине. Сдвиг фаз можно измерить в градусах, от 0 до 360.

На практике степень реактивности (без указания индуктивного либо емкостного характера) выражают не в градусах, а в функции косинуса, и называют коэффициентом мощности:

где:

• P – активная мощность, которая тратится на совершение полезной работы,
• S – полная мощность.

Полная мощность является геометрической суммой активной Р и реактивной Q мощностей, поэтому формулу коэффициента мощности можно записать в следующем виде:

Повторяю: Кто хочет, почитайте про cos φ в Википедии, а я рассказываю своими словами.

В иностранной литературе cos φ называют PF (Power Factor). Фактически, это коэффициент, который говорит о сдвиге сигнала тока по отношению к сигналу напряжения.

На самом деле, всё не так просто, подробности ниже.

Легендарный Алекс Жук очень толково рассказал, что такое реактивная мощность, и всё по этой теме:

В видео подробно и доступно изложена вся теория по теме.

Размерности. Что в чём измеряется

Где нет измерений – там нет науки.

Активная мощность Р ⇒ Вт (то, что измеряет домашний счетчик. Точнее, данные, которые мы пишем в квитанцию оплаты за свет),

Реактивная мощность Q ⇒ ВАР (Вольт · Ампер Реактивный),

Полная мощность S ⇒ ВА (Вольт · Ампер).

Кстати, в стабилизаторах и генераторах мощность указана в ВА. Так больше. Маркетологи знают лучше.
Также маркетологи знают, что на потребителях (например, на двигателях) мощность лучше указывать в кВт. Так меньше.

Минусы и плюсы наличия реактивной составляющей

При питании нагрузки, имеющей только активный характер, сдвиг фаз между током и напряжений равен нулю. Этот случай можно назвать идеальным, при нем можно питающие сети используются полностью, поскольку нет потерь на бесполезную реактивную составляющую.

Реактивная составляющая не так бесполезна. Она формирует электромагнитное поле, нужное для адекватной работы реактивной нагрузки.

В реальной жизни нагрузка, как правило, имеет индуктивный характер (ток отстает от напряжения), и является активно-реактивной. Поэтому всегда, когда говорят о сдвиге фаз и о косинусе, имеют ввиду индуктивную нагрузку.

Основными источниками реактивной составляющей электроэнергии являются трансформаторы и асинхронные электродвигатели.

Чисто реактивная (и чисто активная) нагрузка бывает только в учебнике. Реально за счет потерь всегда присутствует и активная составляющая тоже.

Реактивная составляющая мощности питания является негативным фактором, поскольку:

• Возникают дополнительные потери в линиях передачи электроэнергии,
• Снижается пропускная способность линий электропередачи,
• Происходит падение напряжения на линиях передачи из-за увеличения реактивной составляющей тока питающей сети,
• Происходит дополнительный нагрев и износ систем распределения и трансформации электроэнергии,
• Возможно появление резонансных эффектов на частотах гармоник, что может вызвать перегрев питающих сетей.

По приведенным причинам необходимо понижать долю реактивной мощности в сети (повышать косинус) – это выгодно и энергоснабжающим организациям, и потребителям с распределенными сетями.

Пример: Для передачи определенной мощности нужен ток 100 А при cos φ = 1. Однако, при cos φ = 0,6 для обеспечения той же мощности нужно будет передать ток 166 А! Соответственно, нужно думать о повышении мощности питающей сети и увеличении сечения проводов…

Коэффициент реактивной мощности Тангенс φ

Часто более удобным является коэффициент реактивной мощности tg φ, который показывает отношение реактивной мощности к активной. Понятно, что при tg φ = 0 достигается идеал cos φ = 1.

Отрицательный косинус

Из школьного курса геометрии известно, что cos (φ) = cos (-φ), то есть косинус любого угла будет положительной величиной.

Речь идёт, конечно, о диапазоне сдвига фаз, который физически возможен в энергетике.

Но как же отличить индуктивную нагрузку от емкостной? Всё просто – электрики всех стран условились, что при емкостной нагрузке перед знаком косинуса ставится минус!

В практике пользования прибором анализа напряжения HIOKI у меня были случаи, когда значение косинуса было отрицательным. В последствии выяснилось, что была неправильно включена компенсаторная установка и произошла перекомпенсация. То есть cos φ < 0, что и должно быть, но конденсаторные установки используются неправильно, и возможны ситуации, когда напряжение в сети из-за этого может подняться.

В следующей статье я расскажу не только про косинус, но и про синус применительно к энергетике. А также, как с этим связаны гармоники питающего напряжения

Источник статьи.

Доходчиво ли я изложил? Делитесь в комментариях, будет интересно почитать!

Если интересны темы канала, заходите также на мой сайт – https://samelectric.ru/ и в группу ВК – https://vk.com/samelectric

Статьи в тему производства:

Некоторые мои статьи на Дзене про электродвигатели и пром.оборудование:

Не забываем подписываться и ставить лайки, впереди много интересного!

Обращение к хейтерам:
за оскорбление Автора и Читателей канала – отправляю в баню.