Как найти косинус угла между гранями тетраэдра - Сайт, где вы сможете решить свои вопросы

Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)

Краткая теория

Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.

Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.

Пример решения задачи

Задача

Даны координаты
вершин пирамиды
. Найти:

Сделать чертеж.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Длина ребра

Длину ребра

найдем по
формуле расстояния между 2-мя точками:

Угол между ребрами

найдем как угол
между направляющими векторами

Косинус угла между
векторами:

Угол между ребром и гранью. Векторное произведение

Вычислим угол между
ребром

и гранью

Для этого вычислим
координаты нормального вектора плоскости

–им будет
векторное произведение векторов

Найдем векторное произведение. Для этого

вычислим определитель:

Нормальный вектор
плоскости:

Синус угла:

Площадь грани

Вычислим площадь
грани

. Она будет численно равна половине модуля векторного
произведения векторов

Искомая площадь:

Объем пирамиды. Смешанное произведение векторов

Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов

Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:

Искомый объем
пирамиды:

Уравнение прямой в пространстве

Вычислим уравнение
прямой

. Направляющим
вектором искомой прямой является вектор

. Кроме того, прямая проходит через точку

Уравнение искомой
прямой:

Уравнение плоскости

Вычислим уравнение
плоскости

. Нормальный вектор плоскости

. кроме того, плоскость проходит через точку

-уравнение
грани

Уравнение высоты, опущенной на грань

Составим уравнение
высоты, опущенной на грань

из вершины

Нормальный вектор

является
направляющим вектором высоты, кроме того, высота проходит через точку

Искомое уравнение
высоты:

Сделаем схематический чертеж:

Источник

From Wikipedia, the free encyclopedia

The trigonometry of a tetrahedron^[1] explains the relationships between the lengths and various types of angles of a general tetrahedron.

Trigonometric quantities[edit]

Classical trigonometric quantities[edit]

The following are trigonometric quantities generally associated to a general tetrahedron:

The 6 edge lengths – associated to the six edges of the tetrahedron.
The 12 face angles – there are three of them for each of the four faces of the tetrahedron.
The 6 dihedral angles – associated to the six edges of the tetrahedron, since any two faces of the tetrahedron are connected by an edge.
The 4 solid angles – associated to each point of the tetrahedron.

Let ${displaystyle X={overline {P_{1}P_{2}P_{3}P_{4}}}}$ be a general tetrahedron, where ${displaystyle P_{1},P_{2},P_{3},P_{4}}$ are arbitrary points in three-dimensional space.

Furthermore, let $e_{ij}$ be the edge that joins $P_{i}$ and $P_{j}$ and let $F_{i}$ be the face of the tetrahedron opposite the point $P_{i}$ ; in other words:

${displaystyle e_{ij}={overline {P_{i}P_{j}}}}$
${displaystyle F_{i}={overline {P_{j}P_{k}P_{l}}}}$

where and .

Define the following quantities:

Area and volume[edit]

Let $Delta _{i}$ be the area of the face $F_{i}$ . Such area may be calculated by Heron’s formula (if all three edge lengths are known):

$Delta _{i}={sqrt {frac {(d_{jk}+d_{jl}+d_{kl})(-d_{jk}+d_{jl}+d_{kl})(d_{jk}-d_{jl}+d_{kl})(d_{jk}+d_{jl}-d_{kl})}{16}}}$

or by the following formula (if an angle and two corresponding edges are known):

$Delta _{i}={frac {1}{2}}d_{jk}d_{jl}sin alpha _{j,i}$

Let $h_{i}$ be the altitude from the point $P_{i}$ to the face $F_{i}$ . The volume of the tetrahedron is given by the following formula:

${displaystyle V={frac {1}{3}}Delta _{i}h_{i}}$

It satisfies the following relation:^[2]

${displaystyle 288V^{2}={begin{vmatrix}2Q_{12}&Q_{12}+Q_{13}-Q_{23}&Q_{12}+Q_{14}-Q_{24}\Q_{12}+Q_{13}-Q_{23}&2Q_{13}&Q_{13}+Q_{14}-Q_{34}\Q_{12}+Q_{14}-Q_{24}&Q_{13}+Q_{14}-Q_{34}&2Q_{14}end{vmatrix}}}$

where ${displaystyle Q_{ij}=d_{ij}^{2}}$ are the quadrances (length squared) of the edges.

Basic statements of trigonometry[edit]

Affine triangle[edit]

Take the face $F_{i}$ ; the edges will have lengths ${displaystyle d_{jk},d_{jl},d_{kl}}$ and the respective opposite angles are given by $alpha _{l,i},alpha _{k,i},alpha _{j,i}$ .

The usual laws for planar trigonometry of a triangle hold for this triangle.

Projective triangle[edit]

Consider the projective (spherical) triangle at the point $P_{i}$ ; the vertices of this projective triangle are the three lines that join $P_{i}$ with the other three vertices of the tetrahedron. The edges will have spherical lengths $alpha _{i,j},alpha _{i,k},alpha _{i,l}$ and the respective opposite spherical angles are given by $theta _{ij},theta _{ik},theta _{il}$ .

The usual laws for spherical trigonometry hold for this projective triangle.

Laws of trigonometry for the tetrahedron[edit]

Alternating sines theorem[edit]

Take the tetrahedron , and consider the point $P_{i}$ as an apex. The Alternating sines theorem is given by the following identity:

${displaystyle sin(alpha _{j,l})sin(alpha _{k,j})sin(alpha _{l,k})=sin(alpha _{j,k})sin(alpha _{k,l})sin(alpha _{l,j})}$

One may view the two sides of this identity as corresponding to clockwise and counterclockwise orientations of the surface.

The space of all shapes of tetrahedra[edit]

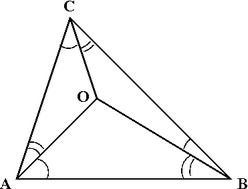
Putting any of the four vertices in the role of O yields four such identities, but at most three of them are independent; if the “clockwise” sides of three of the four identities are multiplied and the product is inferred to be equal to the product of the “counterclockwise” sides of the same three identities, and then common factors are cancelled from both sides, the result is the fourth identity.

Three angles are the angles of some triangle if and only if their sum is 180° (π radians). What condition on 12 angles is necessary and sufficient for them to be the 12 angles of some tetrahedron? Clearly the sum of the angles of any side of the tetrahedron must be 180°. Since there are four such triangles, there are four such constraints on sums of angles, and the number of degrees of freedom is thereby reduced from 12 to 8. The four relations given by the sine law further reduce the number of degrees of freedom, from 8 down to not 4 but 5, since the fourth constraint is not independent of the first three. Thus the space of all shapes of tetrahedra is 5-dimensional.^[3]

Law of sines for the tetrahedron[edit]

See: Law of sines

Law of cosines for the tetrahedron[edit]

The law of cosines for the tetrahedron^[4] relates the areas of each face of the tetrahedron and the dihedral angles about a point. It is given by the following identity:

$Delta _{i}^{2}=Delta _{j}^{2}+Delta _{k}^{2}+Delta _{l}^{2}-2(Delta _{j}Delta _{k}cos theta _{il}+Delta _{j}Delta _{l}cos theta _{ik}+Delta _{k}Delta _{l}cos theta _{ij})$

Relationship between dihedral angles of tetrahedron[edit]

Take the general tetrahedron and project the faces ${displaystyle F_{i},F_{j},F_{k}}$ onto the plane with the face F_l . Let ${displaystyle c_{ij}=cos theta _{ij}}$ .

Then the area of the face F_l is given by the sum of the projected areas, as follows:

${displaystyle Delta _{l}=Delta _{i}c_{jk}+Delta _{j}c_{ik}+Delta _{k}c_{ij}}$

By substitution of with each of the four faces of the tetrahedron, one obtains the following homogeneous system of linear equations:

${displaystyle {begin{cases}-Delta _{1}+Delta _{2}c_{34}+Delta _{3}c_{24}+Delta _{4}c_{23}=0\Delta _{1}c_{34}-Delta _{2}+Delta _{3}c_{14}+Delta _{4}c_{13}=0\Delta _{1}c_{24}+Delta _{2}c_{14}-Delta _{3}+Delta _{4}c_{12}=0\Delta _{1}c_{23}+Delta _{2}c_{13}+Delta _{3}c_{12}-Delta _{4}=0end{cases}}}$

This homogeneous system will have solutions precisely when:

${displaystyle {begin{vmatrix}-1&c_{34}&c_{24}&c_{23}\c_{34}&-1&c_{14}&c_{13}\c_{24}&c_{14}&-1&c_{12}\c_{23}&c_{13}&c_{12}&-1end{vmatrix}}=0}$

By expanding this determinant, one obtains the relationship between the dihedral angles of the tetrahedron,^[1] as follows:

${displaystyle 1-sum _{1leq i<jleq 4}c_{ij}^{2}+sum _{j=2 atop kneq lneq j}^{4}c_{1j}^{2}c_{kl}^{2}=2left(sum _{i=1 atop jneq kneq lneq i}^{4}c_{ij}c_{ik}c_{il}+sum _{2leq j<kleq 4 atop lneq j,k}c_{1j}c_{1k}c_{jl}c_{kl}right)}$

Skew distances between edges of tetrahedron[edit]

Take the general tetrahedron and let $P_{ij}$ be the point on the edge $e_{ij}$ and ${displaystyle P_{kl}}$ be the point on the edge ${displaystyle e_{kl}}$ such that the line segment ${displaystyle {overline {P_{ij}P_{kl}}}}$ is perpendicular to both $e_{ij}$ & ${displaystyle e_{kl}}$ . Let $R_{ij}$ be the length of the line segment ${displaystyle {overline {P_{ij}P_{kl}}}}$ .

To find $R_{ij}$ :^[1]

First, construct a line through ${displaystyle P_{k}}$ parallel to ${displaystyle e_{il}}$ and another line through $P_{i}$ parallel to ${displaystyle e_{kl}}$ . Let be the intersection of these two lines. Join the points and $P_{j}$ . By construction, ${displaystyle {overline {OP_{i}P_{l}P_{k}}}}$ is a parallelogram and thus ${displaystyle {overline {OP_{k}P_{i}}}}$ and ${displaystyle {overline {OP_{l}P_{i}}}}$ are congruent triangles. Thus, the tetrahedron and ${displaystyle Y={overline {OP_{i}P_{j}P_{k}}}}$ are equal in volume.

As a consequence, the quantity $R_{ij}$ is equal to the altitude from the point ${displaystyle P_{k}}$ to the face ${displaystyle {overline {OP_{i}P_{j}}}}$ of the tetrahedron ; this is shown by translation of the line segment ${displaystyle {overline {P_{ij}P_{kl}}}}$ .

By the volume formula, the tetrahedron satisfies the following relation:

${displaystyle 3V=R_{ij}times Delta ({overline {OP_{i}P_{j}}})}$

where ${displaystyle Delta ({overline {OP_{i}P_{j}}})}$ is the area of the triangle ${displaystyle {overline {OP_{i}P_{j}}}}$ . Since the length of the line segment ${displaystyle {overline {OP_{i}}}}$ is equal to ${displaystyle d_{kl}}$ (as ${displaystyle {overline {OP_{i}P_{l}P_{k}}}}$ is a parallelogram):

${displaystyle Delta ({overline {OP_{i}P_{j}}})={frac {1}{2}}d_{ij}d_{kl}sin lambda }$

where ${displaystyle lambda =angle OP_{i}P_{j}}$ . Thus, the previous relation becomes:

${displaystyle 6V=R_{ij}d_{ij}d_{kl}sin lambda }$

To obtain , consider two spherical triangles:

Take the spherical triangle of the tetrahedron at the point $P_{i}$ ; it will have sides $alpha _{i,j},alpha _{i,k},alpha _{i,l}$ and opposite angles $theta _{ij},theta _{ik},theta _{il}$ . By the spherical law of cosines:

${displaystyle cos alpha _{i,k}=cos alpha _{i,j}cos alpha _{i,l}+sin alpha _{i,j}sin alpha _{i,l}cos theta _{ik}}$
Take the spherical triangle of the tetrahedron at the point $P_{i}$ . The sides are given by ${displaystyle alpha _{i,l},alpha _{k,j},lambda }$ and the only known opposite angle is that of , given by ${displaystyle pi -theta _{ik}}$ . By the spherical law of cosines:

${displaystyle cos lambda =cos alpha _{i,l}cos alpha _{k,j}-sin alpha _{i,l}sin alpha _{k,j}cos theta _{ik}}$

Combining the two equations gives the following result:

${displaystyle cos alpha _{i,k}sin alpha _{k,j}+cos lambda sin alpha _{i,j}=cos alpha _{i,l}left(cos alpha _{i,j}sin alpha _{k,j}+sin alpha _{i,j}cos alpha _{k,j}right)=cos alpha _{i,l}sin alpha _{l,j}}$

Making the subject:

${displaystyle cos lambda =cos alpha _{i,l}{frac {sin alpha _{l,j}}{sin alpha _{i,j}}}-cos alpha _{i,k}{frac {sin alpha _{k,j}}{sin alpha _{i,j}}}}$

Thus, using the cosine law and some basic trigonometry:

${displaystyle cos lambda ={frac {d_{ij}^{2}+d_{ik}^{2}-d_{jk}^{2}}{2d_{ij}d_{ik}}}{frac {d_{ik}}{d_{kl}}}-{frac {d_{ij}^{2}+d_{il}^{2}-d_{jl}^{2}}{2d_{ij}d_{il}}}{frac {d_{il}}{d_{kl}}}={frac {d_{ik}^{2}+d_{jl}^{2}-d_{il}^{2}-d_{jk}^{2}}{2d_{ij}d_{kl}}}}$

Thus:

${displaystyle sin lambda ={sqrt {1-left({frac {d_{ik}^{2}+d_{jl}^{2}-d_{il}^{2}-d_{jk}^{2}}{2d_{ij}d_{kl}}}right)^{2}}}={frac {sqrt {4d_{ij}^{2}d_{kl}^{2}-(d_{ik}^{2}+d_{jl}^{2}-d_{il}^{2}-d_{jk}^{2})^{2}}}{2d_{ij}d_{kl}}}}$

So:

${displaystyle R_{ij}={frac {12V}{sqrt {4d_{ij}^{2}d_{kl}^{2}-(d_{ik}^{2}+d_{jl}^{2}-d_{il}^{2}-d_{jk}^{2})^{2}}}}}$

$R_{ik}$ and ${displaystyle R_{il}}$ are obtained by permutation of the edge lengths.

Note that the denominator is a re-formulation of the Bretschneider-von Staudt formula, which evaluates the area of a general convex quadrilateral.

References[edit]

^ ^a ^b ^c Richardson, G. (1902-03-01). “The Trigonometry of the Tetrahedron”. The Mathematical Gazette. 2 (32): 149–158. doi:10.2307/3603090. JSTOR 3603090.
^ 100 Great Problems of Elementary Mathematics. New York: Dover Publications. 1965-06-01. ISBN 9780486613482.
^ Rassat, André; Fowler, Patrick W. (2004). “Is There a “Most Chiral Tetrahedron”?”. Chemistry: A European Journal. 10 (24): 6575–6580. doi:10.1002/chem.200400869. PMID 15558830.
^ Lee, Jung Rye (June 1997). “The law of cosines in a tetrahedron”. J. Korea Soc. Math. Educ. Ser. B: Pure Appl. Math. 4 (1): 1–6. ISSN 1226-0657.

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Скачиваний:

109

Добавлен:

16.03.2016

Размер:

1.78 Mб

Скачать

Гл а в а 6

Тетраэдр

§1. Медианы и бимедианы тетраэдра. Центроид

1.1.Бимедианы (средние линии) тетраэдра. Простейшим многогранником является тетраэдр — четырехгранник. Он обладает многими замечательными свойствами, совокупность которых принято называть геометрией тетраэдра. В этой главе излагаются ее начала.

Отрезки, каждый из которых соединяет середины противоположных (скрещивающихся) ребер тетраэдра, называются его бимедианами (средними линиями).

Теорема 1. Бимедианы тетраэдра пересекаются в одной точке, которая делит пополам каждую из них.

Д о к а з а т е л ь с т в о 1. Пусть MN, EF и P Q — бимедианы тетраэдра ABCD, соответствующие парам ребер AB и CD, AC и BD, BC и AD (рис. 74). Так как отрезки ME и F N параллельны BC и равны

Рис. 74

половине BC, то четырехугольник EMF N — параллелограмм. Точка G пересечения его диагоналей MN и EF делит их пополам. Из параллелограмма EP F Q следует, что середины бимедиан EF и P Q совпадают с точкой G.

Рис. 75

До к а з а т е л ь с т в о 2. Для произвольной точки O векторы OM =

=12 (OA + OB) и ON = 12 (OC + OD). Поэтому 12 (OM + ON) = 14 (OA +

+ OB + OC + OD). Следовательно, вектор OG середины G отрезка MN имеет выражение

(

(6.1)

в которое векторы вершин тетраэдра входят равноправно (симметрично). Это значит, что векторы середин отрезков EF и P Q также равны OG, т. е. середины бимедиан MN, EF и P Q совпадают. Точка G пересечения бимедиан тетраэдра называется его центроидом. Для произвольной точки O вектор OG центроида тетраэдра имеет

выражение (6.1).

1.2. Медианы тетраэдра. Отрезки, каждый из которых соединяет вершину тетраэдра с центроидом противоположной грани, называются

медианами тетраэдра.

Теорема 2. Медианы тетраэдра пересекаются в его центроиде и делятся им в отношении 3 : 1, считая от вершин.

Д о к а з а т е л ь с т в о 1. Пусть G1 и G2 — центроиды граней BCD

иACD тетраэдра ABCD (рис. 75). Они принадлежат медианам BN

иAN этих граней. По свойству цен-

троида треугольника AG2 : G2N = 2

иBG1 : G1N = 2. По обратной теореме Фалеса G1G2 k AB. На основании свойства трапеции прямые AG1, BG2

иMN пересекаются в одной точке K.

G2	D	По теореме Менелая для треугольни-

ка AMN и прямой BG2 имеем:

B	N	AB	·	MK	·	NG2	= −1,
G1	BM	KN	G2A

Cоткуда −2 MK · 12 = −1 и MK : KN =KN

= 1, т. е. точка K является серединой

бимедианы MN и потому совпадает

с центроидом G тетраэдра. Итак, две медианы AG1 и BG2 пересекаются в центроиде G. Значит, все четыре медианы имеют общую точку G. По теореме Менелая для треугольника ABG1 и прямой MN

AM · BN · G1G = −1,

MB NG1 GA

G1G

или 1 · (−3) ·

= −1, откуда G1G : GA =

. Ясно, что это отношение

не зависит от выбора медианы.

Д о к а з а т е л ь с т в о 2.

Возьмем одну медиану AG1 и разделим ее

в отношении 3 : 1 некоторой точкой P :

OA + 3OG1

где

(

OG1

1 + 3

Тогда OP = 14 (OA + OB + OC + OD) = OG и точка P совпадает с G. Следовательно, все четыре медианы тетраэдра содержат его центроид и делятся им в отношении 3 : 1, считая от вершин.

1.3. Свойства центроида тетраэдра. Для того чтобы точка G была центроидом тетраэдра ABCD, необходимо и достаточно, чтобы


GA + GB + GC + GD = 0.	(6.2)

Д о к а з а т е л ь с т в о. Если G — центроид тетраэдра ABCD, то имеет место равенство (6.1) для произвольной точки O. Когда точка O совпадает с G, то OG = 0 и (6.1) принимает вид (6.2). Обратно,

пусть для некоторой точки G имеет место равенство (6.2), из которого GA + GB = −(GC + GD), или 12 (GA + GB) = −12 (GC + GD), или

GM = −GN, где M и N — середины ребер AB и CD. Следовательно, точка G является серединой бимедианы MN, т. е. центроидом тетраэдра. Другое свойство центроида тетраэдра связано с объемами: тетра-

эдры GBCD, GCDA, GDAB, GABC равновелики.

Действительно, отношение высот AH и GH1 тетраэдров ABCD и GBCD равно отношению AG1 : GG1 = 14 (рис. 75). Эти тетраэдры име-

ют общее основание BCD. Значит, VGBCD = 14 VABCD. Объем каждого из четырех указанных тетраэдров равен четверти объема данного тетраэдра.

В силу этого свойства центроид тетраэдра называют еще центром тяжести этого тетраэдра.

Теорема 3 (Лейбница). Сумма квадратов расстояний от произвольной точки P до вершин тетраэдра A1A2A3A4 равна сумме квадратов расстояний от его центроида G до вершин, сложенной с учетверенным квадратом расстояния от точки P до центроида G:

P Ai2 =	GAi2 + 4P G2.	(6.3)
i=1	i=1

Действительно, P Ai = GAi − GP , откуда

P Ai2 = GAi2 − 2GAi · GP + GP 2

и поэтому

4	4	4
X	X		Xi
	P Ai2 = GAi2 − 2	GP		GAi	+ 4P G2.
i=1	i=1	=1

Так как GAi = 0, то равенство (6.3) доказано.

i=1

Из теоремы Лейбница следует экстремальное свойство центроида тетраэдра: сумма квадратов расстояний от точки до вершин тетраэдра минимальна для его центроида. Оно является характеристическим

свойством центроида тетраэдра.

З а д а ч а. Выразите длину бимедианы тетраэдра через длины его ребер.

Р е ш е н и е. Обозначим DA = a, DB = b, DC = c. Тогда

NM = 12 (a + b − c), и NM2 = 14 (a2 + b2 + c2 + 2ab − 2ac − 2bc).

Пусть |AB| = c1, |AC| = b1, |BC| = a1. Так как 2ab = a2 + b2 − c21, 2ac = = a2 + c2 − b21, 2bc = b2 + c2 − a21, то проведя подстановки, получим:

MN2 =	1	(a2 + a12 + b2 + b12 − c2 − c12).	(6.4)
4

Аналогично

EF 2 = 14 (a2+ a21+ c2+ c21−b2−b21), P Q2 = 14 (b2+ b21+ c2+ c21−a2−a21).

Отсюда следует:
MN2 + EF 2 + P Q2 = 41 (a2 + b2 + c2 + a12 + b12 + c12).	(6.5)

§2. Площади граней тетраэдра

2.1.Теорема косинусов для тетраэдра. Квадрат площади любой грани тетраэдра равен сумме квадратов площадей трех остальных его граней без удвоенных произведений площадей этих граней, взятых попарно, и косинусов двугранных углов между ними.

Д о к а з а т е л ь с т в о 1. Воспользуемся формулой (3.3) ортогональной проекции трех граней на плоскость четвертой грани, применяя ее

для каждой грани тетраэдра ABCD:

S1 = S2 cos(CD) + S3 cos(BD) + S4 cos(BC),

S2 = S1 cos(CD) + S3 cos(AD) + S4 cos(AC),

(6.6)

S3 = S1 cos(BD) + S2 cos(AD) + S4 cos(AB), S4 = S1 cos(BC) + S2 cos(AC) + S3 cos(AB).

Умножим эти равенства соответственно на S1, S2, S3, S4 и затем найдем:

S42 − S12 − S22 − S32 = −2S1S2 cos(CD) − 2S2S3 cos(AD) − 2S1S3 cos(BD),

или

S42 = S12 + S22 + S32 − 2S1S2 cos(CD) − 2S2S3 cos(AD) − 2S1S3 cos(BD),

(6.7)

что и утверждает теорема косинусов.

В частности, если двугранные углы при ребрах AD, BD, CD прямые, то

S42 = S12 + S22 + S32.

(6.8)

Соотношение (6.8) представляет собой стереометрический аналог теоремы Пифагора. Д о к а з а т е л ь с т в о 2. Привлечем векторы ni, рассмотренные при решении задачи § 2 гл. 5. Сумма их равна нуль-вектору. Равенство

−n4 = n1 + n2 + n3 возведем скалярно в квадрат:

n24 = n21 + n22 + n23 + 2n1 n2 + 2n2 n3 + 2n1 n3.

Косинус угла между гранями тетраэдра отличается лишь знаком от косинуса угла между перпендикулярными к ним векторами ni, а |ni| = Si. Тогда снова приходим к зависимости (6.7).

2.2. Сумма квадратов площадей граней тетраэдра равна сумме квадратов площадей трех непараллельных граней описанного около него параллелепипеда.

Д о к а з а т е л ь с т в о 1. Определение описанного параллелепипеда дано в п. 3.2 гл. 1. Воспользуемся результатом задачи п. 1.4 гл. 3, согласно которому

2 2 − 1 · 2 2

S1 + S2 2S1S2cos(CD) = 4 AB CD sin(AB, CD) = F1 .

Правая часть этого равенства представляет собой квадрат площади F соответствующей грани описанного параллелепипеда. Аналогично

S12 + S32 − 2S1S3 cos(BD) = F22,

S12 + S42 − 2S1S4 cos (BC) = F32.

Складывая эти три равенства, получим:

F12 + F22 + F32 =

= S22 + S32 + S42 − 2S1(S2 cos(CD) + S3 cos(BD) + S4 cos(BC)) + 3S12 =

= S22 + S32 + S42 − 2S1S1 + 3S12 = S12 + S22 + S32 + S42.

Д о к а з а т е л ь с т в о 2.

Используем

принятые

обозначения. По

определению векторного произведения

(2S1)2 = (

)2, (2S2)2 = (

)2, (2S3)2 = (

)2,

(2S4)2 = (

−

) × (

−

)

2 , (2F1)2 =

× (

−

)

2 ,

(2F2)2 =

2 ,

(2F3)2

= a

(

2 .

−

Тогда доказываемое равенство принимает вид:

(a × b)2 + (b × c)2 + (c × a)2 + (a − b) × (a − c) 2 =

=a × (b − c) 2 + b × (a − c) 2 + c × (b − a) 2 .

Оно верно, так как обе части легко преобразуются к одному и тому же выражению

2 (a × b)2 + (b × c)2 + (c × a)2+

+ (a × b)(b × c) + (b × c)(c × a) + (c × a)(a × b) .

2.3. Зависимость между косинусами двугранных углов тетраэдра.

Запишем систему (6.6) так:

−S1 cos(CD) − S2	+	S3 cos(AD) + S4 cos(AC) = 0,
	S1	+ S2 cos(CD) +	S3 cos(BD) + S4 cos(BC) = 0,
S1 cos(BD) + S2 cos(AD)		S3	+ S4 cos(AB) = 0,

			−	= 0.
	S1 cos(BC) + S2 cos(AC) + S3 cos(AB) − S4

Она является линейной однородной системой относительно S1, S2, S3, S4. Так как она заведомо имеет ненулевое решение, то ее определитель

необходимо равен нулю:

−1	cos(CD)	cos(BD) cos(BC)
	−1	−
cos(CD)	cos(AD)	cos(AC)	= 0.	(6.9)
	cos(AD)	1
cos(BD)	cos(AB)
			−
	cos(AC)	cos(AB)		1
cos(BC)

§3. Объем тетраэдра и объем клина

3.1.Первая формула Штаудта. За исходные формулы объема тетраэдра возьмем две известные формулы:

V =	1	Sh и V =	1	\|	(6.10)

abc\|,
3	6

где a, b, c — векторы трех ребер тетраэдра с общим началом в его вершине. Выведем другие формулы объема тетраэдра.

Пусть AH — высота тетраэдра ABCD, AP — высота его грани

ACD (рис. 76). Тогда AH = AP sin(CD) = a sin ADC sin(CD). Поэтому

V = 3 SBCD ·AH =

6 abc sin ADC sin BDC sin(CD).

Произведение sin ADC sin BDC sin(CD) есть си-

нус Штаудта Δ(D) трехгранного угла D(ABC).

Итак,

V =

abcΔ(D).

(6.11)

Эта формула известна под именем немецкого гео-

метра Карла Штаудта (1798–1867), профессора

Рис. 76

Эрлангенского университета. Без использования обозначений ее можно высказать так: объем тетраэдра равен шестой части произведения длин трех ребер с общей вершиной и синуса Штаудта его триэдра с этой вершиной.

Формула V = 16 |abc| следует из геометрического смысла модуля смешанного произведения векторов (п. 1.3, гл. 5). Из нее сразу же получается формула (6.11), если принять во внимание выражение (5.19) синуса Штаудта через смешанное произведение единичных векторов ребер триэдра:

V = 16 |abc| = 16 abc|abcabc | = 16 abcΔ(D),

abc

так как

abc

= Δ(D).

3.2. Формулы

Достора. По формуле Штаудта

V =

abc sin ADCsin BDCsin(CD) =

bc sin ADC ac sin BDC

sin(CD)

· 2S12S2

Итак,

V =

S1S2

sin(CD)

(6.12)

Аналогично

V =	2	S3S4	sin(AB)	=	2	S1S3	sin(BD)	= . . .
3	AB	3	BD

Следствие. Умножим почленно два из этих равенств:

V 2 =

(S1S2)(S1S3)

sin(CD) sin(BD)

sin BDC

(D)

Произведение sin(CD) sin(BD) sin BDC есть синус второго рода

триэдра D(ABC)

(п. 3.3, гл. 2),

. Следова-

а CD · BD sin BDC = 2S1

тельно,

V 2 =

S1S2S3 · 0(D).

(6.13)

3.3. Формула Сервуа. Используем параллелепипед, описанный около данного тетраэдра ABCD. Четыре тетраэдра, дополняющие данный тетраэдр до этого параллелепипеда, равновелики. Объем каждого из них равен 1/6 объема V параллелепипеда. Поэтому

D		1	1
VABCD = V − 4	· 6 V = 3 V.

		Объем тетраэдра составляет треть объема
		описанного около него параллелепипеда.
d	Q	Высота параллелепипеда равна расстоя-
A	нию d между противоположными ребрами

C		тетраэдра, а площадь основания равна поло-
P		вине произведения длин этих ребер и синуса
	B
	угла f между ними. Таким образом,

Рис. 77

VABCD =	1	aa1d sin f.	(6.14)
6

Приведем еще два доказательства формулы Сервуа (6.14). Дополним тетраэдр ABCD до треугольной призмы (рис. 77), объем

которой втрое больше объема данного тетраэдра и равен половине площади aa1 sin f боковой грани, умноженной на расстояние d от ребра DA до этой грани. В результате получается формула (6.14).

Векторное доказательство ее таково. Пусть P Q — общий перпендикуляр ребер BC и DA. Тогда DC = DQ+ QP + P C и поэтому получаем:

6V = DA DB DC = DA DC + CB DC = DA CB DC =

= DA CB(DQ + QP + P C) = DA CB QP = (DA × CB)QP .

Векторы DA × CB и QP коллинеарны, поэтому их скалярное произведение равно произведению их модулей. А поскольку |DA × CB| = aa1 ×

× sin f и |QP | = d, то 6V = aa1d sin f. Здесь учтено, что первоначальная тройка векторов правая.

Из формулы Сервуа следует теорема Штейнера: объем тетраэдра не изменяется, если его противоположные ребра перемещать без изменения длины по прямым, содержащим эти ребра.

3.4. Теоремы синусов для тетраэдра. Из приведенных формул объема тетраэдра в качестве следствий получаются соотношения, очень похожие на теоремы синусов для треугольника и триэдра.

По формуле Штаудта

6V = abcΔ(D) = a1b1cΔ(C) = a1bc1Δ(B) = ab1c1Δ(A).

Разделим эти равенства почленно на произведение abca1b1c1:

´(A)	=	´(B)	=	´(C)	=	´(D)	=	6V	.	(6.15)
a1bc		ab1c			abc
		abc1		abca1b1c1

Синусы Штаудта трехгранных углов тетраэдра пропорциональны произведениям длин трех ребер граней, противолежащих этим углам

(первая теорема синусов).

Пользуясь формулой (6.13), аналогичным путем получаем:

´0(A)	=	´0(B)	=	´0(C)	=	´0(D)	=	9V 2	.	(6.16)

S1	S2	S3	S4	2S1S2S3S4

Синусы второго рода трехгранных углов тетраэдра пропорциональны площадям противолежащих им граней (вторая теорема синусов).

Далее, перемножим два равенства из (6.12):

V 2 =	4	S1S2S3S4	sin(AB) sin(CD)	.
9
		AB · CD

Из этого соотношения и двух ему аналогичных следует:

AB · CD	=	BC · AD	=	AC · BD	=	4S1S2S3S4	. (6.17)
9V 2
sin(AB) sin(CD)		sin(BC) sin(AD)		sin(AC) sin(BD)

Произведения длин противоположных ребер тетраэдра пропорциональны произведениям синусов соответствующих двугранных углов

(третья теорема синусов).

3.5. Выражение объема тетраэдра через длины его ребер (формула Юнгиуса). Применим формулу (5.15) квадрата смешанного произведения:

(6V )2 = (

)2 =

abc

Умножим каждую строку этого определителя на 2 и все удвоенные скалярные произведения заменим по теореме косинусов для треугольника:

36V 2 = 81 a2 + b2

c12

2b2−

+ c2 −a12 .

+ b2

+ c2

b12

+ c2 − b2

b2 + c2

2c2−

−

Представим полученный определитель в раскрытом виде. После надлежащих преобразований имеем окончательно:

144V 2 = a2a21(b2 + b21 + c2 + c21 − a2 − a21)+

+b2b21(c2 + c21 + a2 + a21 − b2 − b21) + c2c21(a2 + a21 + b2 + b21 − c2 − c21)−

−(bca1)2 − (cab1)2 − (abc1)2 − (a1b1c1)2. (6.18)

Эта формула впервые была найдена другим путем немецким ученым

И.Юнгиусом (1587–1657) и называется его именем.

3.6.Вторая формула Штаудта. Сообщим пока без доказательства еще одну формулу К. Штаудта:

где R — радиус описанной около тетраэдра сферы и

16Q2 = (aa1 + bb1 + cc1)(bb1 + cc1 − aa1)(cc1 + aa1 − bb1)(aa1 + bb1 − cc1).

Доказательство будет дано в § 4 гл. 8.

Важное значение соотношения (6.19) состоит еще и в том, что оно позволяет получить выражение диаметра описанной около тетраэдра сферы через длины его ребер, если привлечь формулу (6.18):

2 16Q2

(2R) = 144V 2 .

3.7. Объем клина. Клином (косоусеченной призмой) называется
пятигранник ABCA1B1C1, три боковые грани которого — трапеции,
	а основания ABC и A1B1C1 —	треугольники
B	(рис. 78). Боковые ребра AA1, BB1,	CC1 клина по-

C		N	парно параллельны. Обозначим их длины соответ-
		ственно a, b, c.
M		S
A	Клин имеет простую формулу объема:
C1		B1	V = 31 S (a + b + c),	(6.20)
	A1		где S — площадь сечения клина плоскостью, пер-

	Рис. 78	пендикулярной боковым ребрам.

100

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Многогранник с 4 гранями

Правильный тетраэдр
. (Нажмите здесь, чтобы вращаться модель)
Тип	Платоновое тело
Элементы	F = 4, E = 6. V = 4 (χ = 2)
Грани по сторонам	4 {3}
Обозначение Конвея	T
Шлефли символы	{3,3}
h {4,3}, s {2,4}, sr {2,2}
Конфигурация лица	V3.3.3
символ Wythoff	3 \| 2 3. \| 2 2 2
Диаграмма Кокстера	= . .
Симметрия	Td, A 3, [3,3], (* 332)
Группа вращения	T, [3,3], (332)
Ссылки	U 01, C 15, W 1
Свойства	правильный, выпуклый дельтаэдр
Двугранный угол	70,528779 ° = arccos (⁄ 3)
. 3.3. 3. (Вершинная фигура )	. Самодвойственный. (двойной многогранник )
. Сеть

Тетраэдр (Matemateca IME-USP )3D-модель правильного тетраэдра.

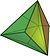
В геометрия, тетраэдр (во множественном числе: тетраэдры или тетраэдры ), также известная как треугольная пирамида, представляет собой многогранник, состоящий из четырех треугольных граней, шести прямых ребер и четырех вершинных углов. Тетраэдр является самым простым из всех обычных выпуклых многогранников и единственным, у которого меньше пяти граней.

Тетраэдр – это трехмерный случай более общей концепции евклидова симплекса, и, таким образом, также может быть называется 3-симплексом .

Тетраэдр – это один из видов пирамиды, который представляет собой многогранник с плоским основанием многоугольника и треугольными гранями, соединяющими основание с общей точкой. В случае тетраэдра основанием является треугольник (любая из четырех граней может считаться основанием), поэтому тетраэдр также известен как «треугольная пирамида».

Как и все выпуклые многогранники, тетраэдр можно сложить из одного листа бумаги. У него две такие сети.

Для любого тетраэдра существует сфера (называемая описанной сферой ), на которой лежат все четыре вершины, и другая сфера (Insphere ) касательная к граням тетраэдра.

Содержание

1 Правильный тетраэдр
- 1.1 Координаты правильного тетраэдра
- 1.2 Углы и расстояния
- 1.3 Изометрии правильного тетраэдра
- 1.4 Ортогональные проекции правильного тетраэдра
- 1.5 Поперечное сечение правильного тетраэдра
- 1.6 Сферическая мозаика
- 1.7 Спиральная укладка
2 Другие частные случаи
- 2.1 Изометрии неправильных тетраэдров
3 Общие свойства
- 3.1 Объем
  - 3.1.1 Формула типа Герона для объема тетраэдра
  - 3.1.2 Разделитель объема
  - 3.1.3 Неевклидов объем
- 3.2 Расстояние между краями
- 3.3 Свойства аналогично треугольнику
- 3.4 Геометрические соотношения
- 3.5 Закон синусов для тетраэдров и пространства всех форм тетраэдров
- 3.6 Закон синусов косинусы тетраэдров
- 3.7 Внутренняя точка
- 3.8 Inradius
- 3.9 Circumradius
- 3.10 Circumcenter
- 3.11 Centroid
- 3.12 Faces
4 Целочисленные тетраэдры
5 Родственные многогранники и соединения
6 Приложения
- 6.1 Численный анализ
- 6.2 Химия
- 6.3 Электричество и электроника
- 6.4 Игры
- 6.5 Цветовое пространство
- 6.6 Современное искусство
- 6.7 Популярная культура
- 6.8 Геология
- 6.9 Структурная инженерия
- 6.10 Авиация
7 Тетраэдрический граф
8 См. Также
9 Ссылки
10 Внешние ссылки

Правильный тетраэдр

A Правильный тетраэдр является тетраэдром в все четыре грани которого являются равносторонними треугольниками. Это одно из пяти правильных Платоновых тел, известных с древних времен.

В правильном тетраэдре все грани имеют одинаковый размер и форму (конгруэнтны), и все ребра имеют одинаковую длину.

Пять тетраэдров уложены на плоскости, причем самые высокие трехмерные точки отмечены цифрами 1, 2, 3, 4 и 5. Затем эти точки соединяются друг с другом и тонкий объем пустого пространства Остается, где пять углов ребер не полностью пересекаются.

Обычные тетраэдры сами по себе не тесселяция (заполнение пространства), но если они чередуются с правильными октаэдрами в При соотношении двух тетраэдров к одному октаэдру они образуют чередующиеся кубические соты , которые представляют собой мозаику. Некоторые тетраэдры, которые не являются правильными, включая ортосхему Шлефли и тетраэдр Хилла, могут быть мозаичными.

Правильный тетраэдр самодвойственен, что означает, что его двойственный является другим правильным тетраэдром. Составная фигура , содержащая два таких двойных тетраэдра, образует звездчатый октаэдр или октангулу стелла.

Координаты правильного тетраэдра

Следующие декартовы координаты определяют четыре вершины тетраэдра с длиной ребра 2 с центром в начале координат и двумя ребрами уровня:

(± 1, 0, – 1 2) и (0, ± 1, 1 2) { displaystyle left ( pm 1,0, – { frac {1} { sqrt {2}}} right) quad { mbox {and}} quad left (0, pm 1, { frac {1} { sqrt {2}}} right)} ${ displaystyle left ( pm 1, 0, - { frac {1} { sqrt {2}}} right) quad { mbox {and}} quad left (0, pm 1, { frac {1} { sqrt {2}}} right)}$

Выражается симметрично как 4 точки на единичной сфере, центр тяжести в начале координат, с уровнем нижней грани, вершины:

v 1 = (8 9, 0, – 1 3) { displaystyle v_ {1} = left ({ sqrt { frac {8} {9}}}, 0, – { frac {1} {3}} right)} ${ displaystyle v_ {1} = left ({ sqrt { frac {8} {9}}}, 0, - { frac {1} {3}} right)}$

v 2 = (- 2 9, 2 3, – 1 3) { displaystyle v_ {2 } = left (- { sqrt { frac {2} {9}}}, { sqrt { frac {2} {3}}}, – { frac {1} {3}} right) } ${ displaystyle v_ {2 } = left (- { sqrt { frac {2} {9}}}, { sqrt { frac {2} {3}}}, - { frac {1} {3}} right) }$

v 3 = (- 2 9, – 2 3, – 1 3) { displaystyle v_ {3} = left (- { sqrt { frac {2} {9}}}, – { sqrt { frac {2} {3}}}, – { frac {1} {3}} right)} ${ displaystyle v_ {3} = left (- { sqrt { frac {2} {9}}}, - { sqrt { frac {2} {3}}}, - { frac {1} {3}} right)}$

v 4 = (0, 0, 1) { displaystyle v_ {4} = ( 0,0,1)} ${ displaystyle v_ {4} = (0,0,1)}$

с длиной кромки 8 3 { displaysty le { sqrt { frac {8} {3}}}} ${ displaystyle { sqrt { frac {8} {3}}}}$ .

Еще один набор координат основан на альтернативном кубе или демикубе с длиной ребра 2. Эта форма имеет диаграмму Кокстера и символ Шлефли h {4,3}. Тетраэдр в этом случае имеет длину ребра 2√2. Инвертирование этих координат генерирует двойственный тетраэдр, а пара вместе образует звездчатый октаэдр, вершины которого совпадают с вершинами исходного куба.

Тетраэдр: (1,1,1), (1, −1, −1), (−1,1, −1), (−1, −1,1)

Двойной тетраэдр : (−1, −1, −1), (−1,1,1), (1, −1,1), (1,1, −1)

Правильный тетраэдр ABCD и его описанная сфера

Углы и расстояния

Для правильного тетраэдра с длиной ребра a:

Площадь грани	A 0 = 3 4 a 2 { displaystyle A_ {0} = { frac { sqrt {3 }} {4}} a ^ {2} ,} ${ displaystyle A_ {0} = { frac { sqrt {3}} {4}} a ^ {2} ,}$
Площадь поверхности	A = 4 A 0 = 3 a 2 { displaystyle A = 4 , A_ {0} = { sqrt {3} } a ^ {2} ,} $A = 4 , A_ {0} = { sqrt {3}} a ^ {2} ,$
Высота пирамиды	h = 6 3 a = 2 3 a { displaystyle h = { frac { sqrt {6}} {3}} a = { sqrt { frac {2} {3}}} , a ,} ${ displaystyle h = { frac { sqrt {6}} { 3}} a = { sqrt { frac {2} {3}}} , a ,}$
Расстояние от центра тяжести до вершины	3 4 h = 6 4 a = 3 8 a { displaystyle { frac {3} {4 }} , h = { frac { sqrt {6}} {4}} , a = { sqrt { frac {3} {8}}} , a ,} ${ displaystyle { frac {3} {4}} , h = { frac { sqrt {6}} {4}} , a = { sqrt { frac {3} {8}}} , a ,}$
От края до противоположного расстояние до края	l = 1 2 a { displaystyle l = { frac {1} { sqrt {2}}} , a ,} ${ displaystyle l = { frac {1} { sqrt {2}}} , a ,}$
Объем	V = 1 3 A 0 h = 2 12 a 3 = a 3 6 2 { displaystyle V = { frac {1} {3}} A_ {0} h = { frac { sqrt {2}} {12}} a ^ {3} = { frac {a ^ {3}} {6 { sqrt {2}}}} ,} ${ displaystyle V = { frac {1} {3}} A_ {0} h = { frac { sqrt {2}} {12}} a ^ {3} = { frac {a ^ {3}} {6 { sqrt {2}}}} ,}$
угол грань-вершина-кромка	дуга соз ⁡ (1 3) знак равно arctan ⁡ (2) { displaystyle arccos left ({ frac {1} { sqrt {3}}} right) = arctan left ({ sqrt {2}} right) ,} ${ displaystyle arccos left ({ frac {1} { sqrt {3}}} right) = arctan left ({ sqrt {2}} right) ,}$ . (прибл. 54,7356 °)
угол грань-кромка-грань, т. Е. «Двугранный угол»	arccos ⁡ (1 3) = arctan ⁡ (2 2) { displaystyle arccos left ({ frac { 1} {3}} right) = arctan left (2 { sqrt {2}} right) ,} ${ displaystyle arccos left ({ frac {1 } {3}} right) = arctan left (2 { sqrt {2}} right) ,}$ . (приблизительно 70,5288 °)
Угол вершины-центра-вершины, угол между прямыми от центра тетраэдра до любых двух вершин. Это также угол между границами плато в вершине. В химии это называется тетраэдрическим валентным углом. Этот угол (в радианах) также является длиной дуги геодезического сегмента на единичной сфере, полученной в результате центрального проецирования одного края тетраэдра на сферу.	arccos ⁡ (- 1 3) = 2 arctan ⁡ (2) { displaystyle arccos left (- { frac {1} {3}} right) = 2 arctan left ({ sqrt { 2}} right) ,} ${ displaystyle arccos left (- { frac {1} {3}} right) = 2 arctan left ({ sqrt {2}} right) ,}$ . (приблизительно 109,4712 °)
Телесный угол в вершине, образуемой гранью	arccos ⁡ (23 27) { displaystyle arccos left ( { frac {23} {27}} right)} ${ displaystyle arccos left ({ frac {23} {27} } right)}$ . (примерно 0,55129 стерадиан ). (примерно 1809,8 квадратных градусов )
Радиус описанной сферы	R = 6 4 a = 3 8 a { displaystyle R = { frac { sqrt {6}} {4}} a = { sqrt { frac {3} {8}}} , a ,} ${ displaystyle R = { frac { sqrt {6}} {4}} a = { sqrt { frac {3} {8}}} , a ,}$
Радиус Insphere, касательный к граням	r = 1 3 R = a 24 { displaystyle r = { frac {1} {3}} R = { frac {a} { sqrt {24}}} ,} ${ displaystyle r = { frac {1} {3}} R = { frac {a} { sqrt {24}}} ,}$
Радиус средней сферы, касающийся ребер	r M = r R = a 8 { displaystyle r _ { mathrm {M}} = { sqrt {rR}} = { frac {a} { sqrt {8}}} ,} ${ displaystyle r _ { mathrm {M}} = { sqrt {rR}} = { frac {a} { sqrt {8}}} ,}$
Радиус экзосферы	r E = 6 { displaystyle r _ { mathrm {E}} = { frac {a} { sqrt {6}}} ,} ${ displaystyle r _ { mathrm {E}} = { frac {a} { sqrt {6}}} ,}$
Расстояние до центра экзосферы от противоположной вершины	d VE = 6 2 a = 3 2 a { displaysty le d _ { mathrm {VE}} = { frac { sqrt {6}} {2}} a = { sqrt { frac {3} {2}}} a ,} ${ displaystyle d _ { mathrm {VE}} = { frac { sqrt {6}} {2}} a = { sqrt { frac {3} {2}}} a ,}$

В отношении на базовой плоскости наклон грани (2√2) в два раза больше, чем у кромки (√2), что соответствует тому факту, что расстояние по горизонтали от основания до вершины по краю вдвое больше, чем по медиане грани. Другими словами, если C является центроидом основания, расстояние от C до вершины основания в два раза больше, чем от C до середины края основания. Это следует из того факта, что медианы треугольника пересекаются в его центроиде, и эта точка делит каждый из них на два отрезка, один из которых в два раза длиннее другого (см. доказательство ).

Для правильного тетраэдра с длиной стороны a, радиусом R описывающей его сферы и расстояниями d i от произвольной точки в 3-пространстве до его четырех вершин мы имеем

д 1 4 + д 2 4 + д 3 4 + д 4 4 4 + 16 р 4 9 = (д 1 2 + д 2 2 + д 3 2 + д 4 2 4 + 2 р 2 3) 2; 4 (а 4 + d 1 4 + d 2 4 + d 3 4 + d 4 4) = (а 2 + d 1 2 + d 2 2 + d 3 2 + d 4 2) 2. { displaystyle { begin {align} { frac {d_ {1} ^ {4} + d_ {2} ^ {4} + d_ {3} ^ {4} + d_ {4} ^ {4}} { 4}} + { frac {16R ^ {4}} {9}} = left ({ frac {d_ {1} ^ {2} + d_ {2} ^ {2} + d_ {3} ^ {2} + d_ {4} ^ {2}} {4}} + { frac {2R ^ {2}} {3}} right) ^ {2}; \ 4 left (a ^ {4 } + d_ {1} ^ {4} + d_ {2} ^ {4} + d_ {3} ^ {4} + d_ {4} ^ {4} right) = left (a ^ {2} + d_ {1} ^ {2} + d_ {2} ^ {2} + d_ {3} ^ {2} + d_ {4} ^ {2} right) ^ {2}. end {align}} } ${ displaystyle { begin {align} { frac {d_ {1} ^ {4} + d_ {2} ^ {4} + d_ {3} ^ {4} + d_ {4} ^ {4}} {4}} + { frac {16R ^ {4}} {9}} = left ( { frac {d_ {1} ^ {2} + d_ {2} ^ {2} + d_ {3} ^ {2} + d_ {4} ^ {2}} {4}} + { frac {2R) ^ {2}} {3}} right) ^ {2}; \ 4 left (a ^ {4} + d_ {1} ^ {4} + d_ {2} ^ {4} + d_ {3 } ^ {4} + d_ {4} ^ {4} right) = left (a ^ {2} + d_ {1} ^ {2} + d_ {2} ^ {2} + d_ {3} ^ {2} + d_ {4} ^ {2} right) ^ {2}. End {align}}}$

Изометрии правильного тетраэдра

Собственные вращения (поворот третьего порядка на вершине и грани и второй порядок на двух ребрах) и плоскость отражения (через две грани и одно ребро) в группе симметрии правильного тетраэдра

Вершины куба можно сгруппировать в две группы по четыре, каждая из которых образует правильный тетраэдр (см. выше, а также анимацию, показывающую одну из два тетраэдра в кубе). Симметрии правильного тетраэдра соответствуют половине симметрий куба: симметрии, которые отображают тетраэдры сами по себе, а не друг в друга.

Тетраэдр – единственное платоново твердое тело, которое не отображается на себя с помощью точечной инверсии.

Правильный тетраэдр имеет 24 изометрии, формируя группу симметрии Td, [3,3 ], (* 332), изоморфна симметрической группе, S 4. Их можно разделить на следующие категории:

T, [3,3], (332) изоморфна переменной группе, A 4 (тождество и 11 собственных вращений) с следующие классы сопряженности (в скобках даны перестановки вершин или, соответственно, граней и представление единичного кватерниона ):
- identity (identity; 1)
- поворот вокруг оси через вершину, перпендикулярную противоположной плоскости, на угол ± 120 °: 4 оси, по 2 на каждую ось, вместе 8 ((1 2 3) и т.д.; 1 ± i ± j ± k / 2)
- поворот на угол 180 °, так что край отображается на противоположный край: 3 ((1 2) (3 4) и т.д.; i, j, k)
отражения в плоскости, перпендикулярной краю: 6
отражений в плоскости в сочетании с поворотом на 90 ° вокруг оси, перпендикулярной плоскости: 3 оси, по 2 на каждую ось, вместе 6; эквивалентно, это повороты на 90 ° в сочетании с инверсией (x отображается в – x ): вращения соответствуют поворотам куба относительно осей лицом к лицу

Ортогонально проекции правильного тетраэдра

Правильный тетраэдр имеет две специальные ортогональные проекции, одна с центром на вершине или, что эквивалентно, на грани, и одна с центром на ребре. Первый соответствует плоскости Кокстера A 2.

Ортографическая проекция

Центрированная по	Грань / вершина	Край
Изображение
Проективная. симметрия	[3]	[4]

Поперечное сечение правильного тетраэдра

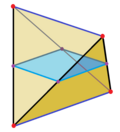Центральное поперечное сечение правильного тетраэдра представляет собой квадрат.

Два скошенных перпендикуляра противоположно ребра правильного тетраэдра определяют набор параллельных плоскостей. Когда одна из этих плоскостей пересекает тетраэдр, результирующее поперечное сечение представляет собой прямоугольник . Когда пересекающаяся плоскость находится рядом с одним из краев, прямоугольник получается длинным и тонким. На полпути между двумя краями пересечение представляет собой квадрат. Соотношение сторон прямоугольника меняется на противоположное, когда вы проходите эту половину пути. Для пересечения квадрата средней точки результирующая граничная линия пересекает каждую грань тетраэдра аналогично. Если тетраэдр делится пополам на этой плоскости, обе половины становятся клиньями.

тетрагональным дифеноидом, если смотреть перпендикулярно двум зеленым краям.

Это свойство также применяется для тетрагональных дифеноидов при применении к две специальные пары кромок.

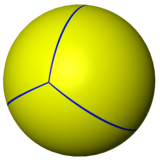
Сферическая мозаика

Тетраэдр также может быть представлен как сферическая мозаика и спроецирован на плоскость через стереографическую проекцию . Эта проекция конформна, сохраняя углы, но не площади или длины. Прямые на сфере проектируются как дуги окружности на плоскость.

Ортографическая проекция	Стереографическая проекция

Спиральное наложение

Одиночное кольцо из 30 тетраэдров Спираль Бурдейка – Кокстера внутри 600-ячеек, в стереографической проекции

Правильные тетраэдры могут быть уложены лицом к лицу в хиральную апериодическую цепочку, называемую спиралью Бурдейка – Кокстера. В четырехмерном все выпуклые правильные 4-многогранники с тетраэдрическими ячейками (5-ячеечная, 16-ячеечная и 600-ячейка ) могут быть построены как мозаики 3-сферы этими цепочками, которые становятся периодическими в трехмерном пространстве граничной поверхности 4-многогранника.

Другие особые случаи

равнобедренный тетраэдр, также называемый дисфеноидом, представляет собой тетраэдр, где все четыре грани – это конгруэнтные треугольники. заполняющий пространство тетраэдр упакован с конгруэнтными копиями самого себя в пространство тайла, как тетраэдрические соты дифеноида.

В треугольном тетраэдре три угла в одной вершине равны прямые углы. Если все три пары противоположных ребер тетраэдра перпендикулярны, то он называется ортоцентрическим тетраэдром. Когда перпендикулярна только одна пара противоположных ребер, это называется полуортоцентрическим тетраэдром . изодинамический тетраэдр – это тетраэдр, в котором чевианы, которые соединяют вершины с центрами противоположных граней, параллельны, а изогонический тетраэдр имеет параллельные чевианы, которые соединяют вершины с точками контакта противоположных граней с вписанной сферой тетраэдра.

Изометрии неправильных тетраэдров

Изометрии неправильных (немаркированных) тетраэдров зависят от геометрии тетраэдра, возможны 7 случаев. В каждом случае формируется 3-мерная точечная группа. Две другие изометрии (C 3, [3]) и (S 4, [2,4]) могут существовать, если включена маркировка граней или кромок. Для каждого типа ниже включены четырехгранные диаграммы с краями, окрашенными в соответствии с изометрической эквивалентностью, и серым цветом для уникальных краев.

Название тетраэдра	Край. эквивалентность. диаграмма	Описание
Симметрия
Шён.	Кокс.	Орб.	Порядок.
Правильный тетраэдр		Четыре равносторонних треугольника Он образует группу симметрии T d, изоморфную симметрической группе, S 4. Правильный тетраэдр имеет диаграмму Кокстера и символ Шлефли {3,3}.
Td. T	[3,3 ]. [3,3 impression	* 332. 332	24. 12
Треугольная пирамида		Основание равностороннего треугольника и три равные стороны равнобедренного треугольника Это дает 6 изометрий, соответствующих 6 изометриям основания. Как перестановки вершин, эти 6 изометрий являются тождеством 1, (123), (132), (12), (13) и (23), образуя группу симметрии C 3v, изоморфную симметричная группа, S 3. Треугольная пирамида имеет символ Шлефли {3} ∨ ().
C3v. C3	[3 ]. [3pting	* 33. 33	6. 3
Зеркальный клиновидный сустав		Два равных разностороннего треугольника с общим краем основания Имеет две пары равных ребер (1,3), (1,4) и (2,3), (2,4) и в противном случае нет равных ребер. Единственными двумя изометриями являются 1 и отражение (34), дающее группу C s, также изоморфную циклической группе, Z2.
Cs. =C1h. =C1v	[]	*	2
Неправильный тетраэдр. (Нет симметрии)		Четыре неравных треугольника Его единственная изометрия – это тождество, а группа симметрии – тривиальная группа. Неправильный тетраэдр имеет символ Шлефли () ∨ () ∨ () ∨ ().
C1	[]	1	1
Дисфеноиды (Четыре равных треугольника)
Тетрагональный дисфеноид		Четыре равных равнобедренныхтреугольников Он имеет 8 изометрий. Если ребра (1,2) и (3,4) имеют длину, отличную от длины остальных 4, то 8 изометрий являются тождественными 1, отражениями (12) и (34) и поворотами на 180 ° (12) (34), (13) (24), (14) (23) и неправильные повороты на 90 ° (1234) и (1432), образующие группу симметрии D 2d. Тетрагональный дисфеноид имеет диаграмму Кокстера и символ Шлефли s {2,4}.
D2d. S4	[2,4 ]. [2,4 ]	2 * 2. 2×	8. 4
Ромбический дисфеноид		Четыре равных скалентреугольника It имеет 4 изометрии. Изометрии равны 1 и повороты на 180 ° (12) (34), (13) (24), (14) (23). Это четырехгруппа Клейна V4или Z2, представленная как точечная группа D 2. Ромбический дисфеноид имеет диаграмму Кокстера и символ Шлефли sr {2,2}.
D2	[2,2 ]	222	4
Обобщенные дисфеноиды (2 пары равных треугольников)
Дигональный дисфеноид	.	Две пары равных равнобедренных треугольников Это дает две противоположные кромки (1,2) и (3,4), которые перпендикулярны, но разной длины, а затем 4 изометрии равны 1, отражениям (12) и (34) и повороту на 180 ° (12) (34).. Группа симметрии – это C 2v, изоморфная четырехгруппе Клейна V4. Дигональный дисфеноид имеет символ Шлефли {} ∨ {}.
C2v. C2	[2 ]. [2 ]	* 22. 22	4. 2
Филлический дисфеноид	.	Две пары равных разносторонних или равнобедренных треугольников Он имеет две пары равных ребер (1,3), (2,4) и (1,4), (2,3), но в остальном нет равных ребер. Единственными двумя изометриями являются 1 и вращение (12) (34), что дает группу C 2, изоморфную циклической группе, Z2.
C2	[2]	22	2

Общие свойства

Объем

Объем тетраэдра определяется формулой объема пирамиды:

V = 1 3 A 0 h { displaystyle V = { frac {1} {3}} A_ {0 } , h ,} ${ displaystyle V = { frac {1} {3}} A_ {0} , h ,}$

где A 0 – это площадь основания, а h – высота от основания до вершины. Это применимо для каждого из четырех вариантов основания, поэтому расстояния от вершин до противоположных граней обратно пропорциональны площадям этих граней.

Для тетраэдра с вершинами a = (a 1, a 2, a 3), b = (b 1, b 2, b 3), c = (c 1, c 2, c 3) и d = (d 1, d 2, d 3), объем равен 1/6 | det (a− d, b− d, c− d) |, или любая другая комбинация пар вершин, образующих односвязный граф . Это можно переписать, используя скалярное произведение и кросс-произведение, что дает

V = | (a – d) ⋅ ((b – d) × (c – d)) | 6. { Displaystyle В = { гидроразрыва {| ( mathbf {a} – mathbf {d}) cdot (( mathbf {b} – mathbf {d}) раз ( mathbf {c} – mathbf {d})) |} {6}}.} $V = { frac {| ( mathbf {a} - mathbf {d }) cdot (( mathbf {b} - mathbf {d}) times ( mathbf {c} - mathbf {d})) |} {6}}.$

Если начало системы координат выбрано таким, чтобы оно совпадало с вершиной d, то d = 0, поэтому

V = | a ⋅ (b × c) | 6, { displaystyle V = { frac {| mathbf {a} cdot ( mathbf {b} times mathbf {c}) |} {6}},} $V = { frac {| mathbf {a} cdot ( mathbf {b } times mathbf {c}) |} {6}},$

где a, b, и c представляют три ребра, которые встречаются в одной вершине, а a · (b× c) представляет собой тройное скалярное произведение. Сравнивая эту формулу с формулой, использованной для вычисления объема параллелепипеда , мы заключаем, что объем тетраэдра равен 1/6 объема любого параллелепипеда, который имеет три сходящихся с ним ребра.

Абсолютное значение скалярного тройного произведения можно представить в виде следующих абсолютных значений определителей:

6 ⋅ V = ‖ abc ‖ { displaystyle 6 cdot V = { begin {Vmatrix} mathbf {a} mathbf {b} mathbf {c} end {Vmatrix}}}

или 6 ⋅ V = ‖ abc ‖ { displaystyle 6 cdot V = { begin {Vmatrix} mathbf {a} \ mathbf {b} \ mathbf {c} end {Vmatrix}}} $6 cdot V = { begin {Vmatrix} mathbf {a} \ mathbf { b} \ mathbf {c} end {Vmatrix}}$

где a = (a 1, a 2, a 3) { displaystyle mathbf {a} = (a_ {1}, a_ {2}, a_ {3}) ,} $mathbf {a} = (a_ {1}, a_ {2}, a_ {3}) ,$

выражается как вектор строки или столбца и т. Д.

Следовательно

36 ⋅ V 2 = | a 2 a ⋅ b a ⋅ c a ⋅ b b 2 b ⋅ c a ⋅ c b ⋅ c c 2 | { Displaystyle 36 cdot V ^ {2} = { begin {vmatrix} mathbf {a ^ {2}} mathbf {a} cdot mathbf {b} mathbf {a} cdot mathbf {c} \ mathbf {a} cdot mathbf {b} mathbf {b ^ {2}} mathbf {b} cdot mathbf {c} \ mathbf {a} cdot mathbf {c} mathbf {b} cdot mathbf {c} mathbf {c ^ {2}} end {vmatrix}}} $36 cdot V ^ {2} = { begin {vmatrix} mathbf {a ^ {2}} mathbf {a} cdot mathbf {b} mathbf {a} cdot mathbf {c} \ mathbf {a} cdot mathbf {b} mathbf {b ^ {2}} mathbf {b} cdot mathbf {c} \ mathbf {a} cdot mathbf {c} mathbf {b} cdot mathbf {c} mathbf {c ^ {2}} end {vmatrix}}$

где a ⋅ b = ab cos ⁡ γ { displaystyle mathbf {a} cdot mathbf {b} = ab cos { gamma}}

и т. Д.

, что дает

V = abc 6 1 + 2 cos ⁡ α соз ⁡ β соз ⁡ γ – соз 2 ⁡ α – соз 2 ⁡ β – соз 2 ⁡ γ, { displaystyle V = { frac {abc} {6}} { sqrt {1 + 2 cos { alpha} cos { beta} cos { gamma} – cos ^ {2} { alpha} – cos ^ {2} { beta} – cos ^ {2} { gamma}}}, ,} $V = { frac {abc} {6}} { sqrt {1 + 2 cos { alpha} cos { beta} cos { gamma} - cos ^ {2} { alpha} - cos ^ {2} { beta} - cos ^ {2} { gamma}}}, ,$

где α, β, γ – плоские углы, входящие в вершину d . Угол α – это угол между двумя ребрами, соединяющими вершину d с вершинами b и c . Угол β имеет значение для вершин a и c, тогда как γ определяется положением вершин a и b.

Учитывая расстояния между вершинами тетраэдра объем может быть вычислен с помощью определителя Кэли – Менгера :

288 ⋅ V 2 = | 0 1 1 1 1 1 0 d 12 2 d 13 2 d 14 2 1 d 12 2 0 d 23 2 d 24 2 1 d 13 2 d 23 2 0 d 34 2 1 d 14 2 d 24 2 d 34 2 0 | { displaystyle 288 cdot V ^ {2} = { begin {vmatrix} 0 1 1 1 1 \ 1 0 d_ {12} ^ {2} d_ {13} ^ {2} d_ {14} ^ {2} \ 1 d_ {12 } ^ {2} 0 d_ {23} ^ {2} d_ {24} ^ {2} \ 1 d_ {13} ^ {2} d_ {23} ^ {2} 0 d_ {34} ^ {2} \ 1 d_ {14} ^ {2} d_ {24} ^ {2} d_ {34} ^ {2} 0 end {vmatrix}}} $288 cdot V ^ {2} = { begin {vmatrix} 0 1 1 1 1 \ 1 0 d_ {12} ^ {2} d_ {13} ^ {2} d_ {14} ^ {2} \ 1 d_ {12} ^ { 2} 0 d_ {23} ^ {2} d_ {24} ^ {2} \ 1 d_ {13} ^ {2} d_ {23} ^ {2} 0 d_ {34} ^ {2} \ 1 d_ {14} ^ {2} d_ {24} ^ {2} d_ {34} ^ {2} 0 end {vmatrix}}$

где нижние индексы i, j ∈ {1, 2, 3, 4} представляют вершины {a, b, c, d}, а d ij – попарное расстояние между ними, то есть длина ребра, соединяющего две вершины. Отрицательное значение определителя означает, что тетраэдр не может быть построен с заданными расстояниями. Эта формула, иногда называемая формулой Тартальи, по существу создана художником Пьеро делла Франческа в 15 веке как трехмерный аналог 1 века формула Герона для площади треугольника.

Обозначим a, b, c три ребра, которые пересекаются в точке, а x, y, z – противоположные стороны. Пусть V – объем тетраэдра; тогда

V = 4 a 2 b 2 c 2 – a 2 X 2 – b 2 Y 2 – c 2 Z 2 + XYZ 12 { displaystyle V = { frac { sqrt {4a ^ {2} b ^ {2} c ^ {2} -a ^ {2} X ^ {2} -b ^ {2} Y ^ {2} -c ^ {2} Z ^ {2} + XYZ}} {12}}} ${ displaystyle V = { frac { sqrt {4a ^ {2} b ^ {2} c ^ {2} -a ^ {2} X ^ {2} -b ^ {2} Y ^ {2} -c ^ {2} Z ^ {2} + XYZ}} {12}}}$

где

X = b 2 + c 2 – x 2 { displaystyle X = b ^ {2} + c ^ {2} -x ^ {2}} ${ displaystyle X = b ^ {2} + c ^ {2} -x ^ {2}}$

Y = a 2 + c 2 – y 2 { displaystyle Y = a ^ {2} + c ^ {2} -y ^ {2}} ${ displaystyle Y = a ^ {2} + c ^ {2} -y ^ {2}}$

Z = a 2 + b 2 – z 2 { displaystyle Z = a ^ {2} + b ^ {2} -z ^ {2}} ${ displaystyle Z = a ^ {2} + b ^ {2} -z ^ {2}}$

В приведенной выше формуле используются различные выражения со следующей формулой. В приведенной выше формуле используются шесть длин ребер, а в следующей формуле используются три длины ребер и три угла.

V = abc 6 1 + 2 cos ⁡ α cos ⁡ β cos ⁡ γ – cos 2 ⁡ α – cos 2 ⁡ β – cos 2 ⁡ γ { displaystyle V = { frac {abc} {6}} { sqrt {1 + 2 cos { alpha} cos { beta} cos { gamma} – cos ^ {2} { alpha} – cos ^ {2} { beta} – cos ^ {2} { gamma}}}} ${ displaystyle V = { frac {abc} {6}} { sqrt {1 + 2 cos { alpha} cos { beta} cos { gamma} - cos ^ {2} { alpha} - cos ^ {2} { beta} - cos ^ {2} { gamma}}}}$

Формула типа Герона для объема тетраэдра

Если U, V, W, u, v, w – длины ребер тетраэдра (первый три образуют треугольник; u напротив U и так далее), тогда

volume = (- a + b + c + d) (a – b + c + d) (a + b – c + d) (a + b + c – d) 192 uvw { displaystyle { text {volume}} = { frac { sqrt {, (- a + b + c + d) , (a-b + c + d) , (a + b-c + d) , (a + b + cd)}} {192 , u , v , w}}} ${ text {volume }} = { frac { sqrt {, (- a + b + c + d) , (a-b + c + d) , (a + b-c + d) , (a + b + cd)}} {192 , u , v , w}}$

где

a = x YZ b = y ZX c = z XY d = xyz X = (w – U + v) (U + v + w) x = (U – v + w) (v – w + U) Y = (u – V + w) ( V + w + u) y = (V – w + u) (w – u + V) Z = (v – W + u) (W + u + v) z = (W – u + v) (u – v + W). { displaystyle { begin {align} a = { sqrt {xYZ}} \ b = { sqrt {yZX}} \ c = { sqrt {zXY}} \ d = { sqrt {xyz} } \ X = (w-U + v) , (U + v + w) \ x = (U-v + w) , (v-w + U) \ Y = (u-V + w) , (V + w + u) \ y = (V-w + u) , (w-u + V) \ Z = (v-W + u) , (W + u + v) \ z = (W-u + v) , (u-v + W). end {align}}} ${ begin {align} a = { sqrt {xYZ}} \ b = { sqrt {yZX}} \ c = { sqrt {zXY}} \ d = { sqrt {xyz}} \ X = (w-U + v) , (U + v + w) \ x = (U-v + w) , (v-w + U) \ Y = ( и-V + w) , (V + w + u) \ y = (V-w + u) , (w-u + V) \ Z = (v-W + u) , (W + u + v) \ z = (W-u + v) , (u-v + W). end {align}}$

Разделитель объема

Плоскость, которая разделяет два противоположных края тетраэдра в заданном соотношении также делит объем тетраэдра в таком же соотношении. Таким образом, любая плоскость, содержащая бимедиан (соединитель середин противоположных ребер) тетраэдра , делит объем тетраэдра пополам.

Неевклидов объем

Для тетраэдров в гиперболическое пространство или в трехмерной эллиптической геометрии, двугранные углы тетраэдра определяют его форму и, следовательно, его объем. В этих случаях объем определяется по формуле Мураками – Яно. Однако в евклидовом пространстве масштабирование тетраэдра изменяет его объем, но не его двугранные углы, поэтому такой формулы не может быть.

Расстояние между краями

Любые два противоположных ребра тетраэдра лежат на двух наклонных линиях, а расстояние между ребрами определяется как расстояние между двумя наклонными линиями. линий. Пусть d будет расстоянием между линиями наклона, образованными противоположными краями a и b− c, как вычислено здесь. Тогда другая формула объема задается как

V = d | (a × (b – c)) | 6. { displaystyle V = { frac {d | ( mathbf {a} times mathbf {(bc)}) |} {6}}.} $V = { frac { d | ( mathbf {a} times mathbf {(bc)}) |} {6}}.$

Свойства, аналогичные свойствам треугольника

Тетраэдр имеет много свойств, аналогичных свойствам треугольника, включая внутреннюю сферу, описанную сферу, средний тетраэдр и внешние сферы. Он имеет соответствующие центры, такие как центр окружности, центр окружности, эксцентрики, центр Шпикера и такие точки, как центроид. Однако обычно нет ортоцентра в смысле пересечения высот.

Гаспар Монж обнаружил центр, который существует в каждом тетраэдре, теперь известный как точка Монжа : точка, в которой находятся шесть срединных плоскостей. тетраэдра пересекаются. Срединная плоскость определяется как плоскость, ортогональная ребру, соединяющему любые две вершины, который также содержит центроид противоположного ребра, образованного путем соединения двух других вершин. Если высоты тетраэдра пересекаются, то точка Монжа и ортоцентр совпадают, давая класс ортоцентрического тетраэдра.

. Ортогональная линия, опущенная от точки Монжа к любой грани, пересекает эту грань в середине отрезка прямой между ортоцентр лица и основание высоты упало с противоположной вершины.

Отрезок, соединяющий вершину тетраэдра с центроидом противоположной грани, называется срединной, а отрезок, соединяющий середины двух противоположных ребер, называется бимедианой тетраэдра.. Следовательно, в тетраэдре четыре медианы и три бимедианы. Все эти семь отрезков параллельны в точке, называемой центроидом тетраэдра. Кроме того, четыре медианы делятся на центроид в соотношении 3: 1 (см. теорему Коммандино ). Центроид тетраэдра – это середина между его точкой Монжа и центром описанной окружности. Эти точки определяют линию Эйлера тетраэдра, которая аналогична прямой Эйлера треугольника.

окружность из девяти точек общего треугольника имеет аналог в описанной сфере среднего тетраэдра тетраэдра. Это сфера с двенадцатью точками и, помимо центроидов четырех граней эталонного тетраэдра, она проходит через четыре замещающие точки Эйлера, по одной трети пути от точки Монжа к каждой из четырех вершин. Наконец, он проходит через четыре базовые точки ортогональных прямых, опущенных от каждой точки Эйлера к грани, не содержащей вершину, которая породила точку Эйлера.

Центр T двенадцатиточечной сферы также лежит на прямой Эйлера. В отличие от своего треугольного аналога, этот центр находится на одной трети пути от точки Монжа M к центру описанной окружности. Кроме того, ортогональная линия, проходящая через точку T к выбранной грани, копланарна с двумя другими ортогональными линиями к той же грани. Первая – это ортогональная линия, проходящая через соответствующую точку Эйлера к выбранной грани. Вторая – это ортогональная линия, проходящая через центр тяжести выбранной грани. Эта ортогональная линия, проходящая через центр из двенадцати точек, находится на полпути между ортогональной линией точки Эйлера и центроидальной ортогональной линией. Кроме того, для любой грани центр из двенадцати точек лежит в средней точке соответствующей точки Эйлера и ортоцентре этой грани.

Радиус двенадцатиточечной сферы составляет одну треть радиуса описанной окружности контрольного тетраэдра.

Существует связь между углами, образованными гранями общего тетраэдра, определяемая как

| – 1 cos ⁡ (α 12) cos ⁡ (α 13) cos ⁡ (α 14) cos ⁡ (α 12) – 1 cos ⁡ (α 23) cos ⁡ (α 24) cos ⁡ (α 13) cos ⁡ (α 23) – 1 cos ⁡ (α 34) cos ⁡ (α 14) cos ⁡ (α 24) cos ⁡ (α 34) – 1 | Знак равно 0 { displaystyle { begin {vmatrix} -1 cos {( alpha _ {12})} cos {( alpha _ {13})} cos {( alpha _ {14}) } \ cos {( alpha _ {12})} – 1 cos {( alpha _ {23})} cos {( alpha _ {24})} \ cos {( alpha _ {13})} cos {( alpha _ {23})} – 1 cos {( alpha _ {34})} \ cos {( alpha _ {14})} cos {( alpha _ {24})} cos {( alpha _ {34})} – 1 \ end {vmatrix}} = 0 ,} ${ begin {vmatrix} -1 cos {( alpha _ {12})} cos {( alpha _ {13 })} cos {( alpha _ {14})} \ cos {( alpha _ {12})} - 1 cos {( alpha _ {23})} cos {( alpha _ {24})} \ cos {( alpha _ {13})} cos {( alpha _ {23})} - 1 cos {( alpha _ {34})} \ cos {( alpha _ {14})} cos {( alpha _ {24})} cos {( alpha _ {34})} - 1 \ end {vmatrix} } = 0 ,$

где α ij – угол между гранями i и j.

геометрическая медиана координат положения вершины тетраэдра и его изогонический центр связаны при обстоятельствах, аналогичных тем, которые наблюдаются для треугольника. Лоренц Линделёф обнаружил, что любому данному тетраэдру соответствует точка, теперь известная как изогонический центр, O, в котором телесные углы, образуемые гранями, равны, имеют общее значение π sr, и при углы между противоположными краями равны. Телесный угол π sr составляет четверть угла, охватываемого всем пространством. Когда все телесные углы в вершинах тетраэдра меньше π sr, O лежит внутри тетраэдра, а поскольку сумма расстояний от O до вершин минимальна, O совпадает с геометрической медианой , M, вершин. В том случае, если телесный угол в одной из вершин, v, составляет ровно π sr, тогда O и M совпадают с v. Однако если у тетраэдра есть вершина v с телесным углом больше π sr, M по-прежнему соответствует к v, но O лежит вне тетраэдра.

Геометрические соотношения

Тетраэдр – это 3- симплекс. В отличие от других Платоновых тел, все вершины правильного тетраэдра равноудалены друг от друга (это единственно возможное расположение четырех равноудаленных точек в трехмерном пространстве).

Тетраэдр – это треугольная пирамида, а правильный тетраэдр – самодвойственный.

. Правильный тетраэдр может быть вложен внутрь куба пополам. таких способов, что каждая вершина является вершиной куба, а каждое ребро – диагональю одной из граней куба. Для одного такого вложения декартовы координаты для вершин равны

(+1, +1, +1);

(−1, −1, +1);

(−1, +1, −1);

(+1, −1, −1).

Это дает тетраэдр с длиной ребра 2√2 с центром в начале координат. Для другого тетраэдра (который двойственен первому) поменяйте все знаки местами. Эти две вершины тетраэдра вместе являются вершинами куба, демонстрируя, что правильный тетраэдр представляет собой 3- полукуб.

stella octangula.

Объем этого тетраэдра составляет одну треть объема куба куб. Объединение обоих тетраэдров дает правильное полиэдрическое соединение, называемое соединением двух тетраэдров или stella octangula.

Внутренняя часть stella octangula представляет собой октаэдр, и, соответственно, правильный октаэдр является результатом отсечения от правильного тетраэдра четырех правильных тетраэдров половинного линейного размера (т. е. выпрямления тетраэдра).

Приведенное выше вложение делит куб на пять тетраэдров, один из которых правильный. Фактически, пять – это минимальное количество тетраэдров, необходимое для создания куба. Чтобы убедиться в этом, начиная с базового тетраэдра с 4 вершинами, каждый добавленный тетраэдр добавляет не более 1 новой вершины, поэтому необходимо добавить еще как минимум 4, чтобы создать куб с 8 вершинами.

Включение тетраэдров внутрь правильного соединения пяти кубов дает еще два правильных соединения, содержащих пять и десять тетраэдров.

Обычные тетраэдры не могут замощить пространство сами по себе, хотя этот результат кажется достаточно вероятным, чтобы Аристотель утверждал, что это возможно. Однако два правильных тетраэдра могут быть объединены с октаэдром, давая ромбоэдр, который может занимать мозаичное пространство.

Однако известно несколько неправильных тетраэдров, копии которых могут занимать мозаичное пространство, например, тетраэдрические соты дифеноида. Полный список остается открытой проблемой.

Если ослабить требование, чтобы все тетраэдры имели одинаковую форму, можно разбить пространство, используя только тетраэдры, разными способами. Например, можно разделить октаэдр на четыре одинаковых тетраэдра и снова объединить их с двумя правильными. (В качестве примечания: эти два вида тетраэдров имеют одинаковый объем.)

Тетраэдр уникален среди однородных многогранников тем, что не имеет параллельных граней.

Закон синусов для тетраэдров и пространства всех форм тетраэдров

Следствием обычного закона синусов является то, что в тетраэдр с вершинами O, A, B, C, имеем

sin ⁡ ∠ O A B ⋅ sin ⁡ ∠ O B C ⋅ sin ⁡ ∠ O C A = sin ⁡ ∠ O A C ⋅ sin ⁡ ∠ O C B ⋅ sin ⁡ ∠ O B A. { displaystyle sin angle OAB cdot sin angle OBC cdot sin angle OCA = sin angle OAC cdot sin angle OCB cdot sin angle OBA. ,}

sin angle OAB cdot sin угол OBC cdot sin angle OCA = sin angle OAC cdot sin angle OCB cdot sin angle OBA. ,

One может рассматривать две стороны этой идентичности как соответствующие ориентации поверхности по часовой стрелке и против часовой стрелки.

Если поставить любую из четырех вершин в роли O, мы получим четыре таких тождества, но не более трех из них независимы: если стороны трех из них «по часовой стрелке» умножаются, и произведение получается равным равняется произведению сторон «против часовой стрелки» тех же трех тождеств, а затем общие множители сокращаются с обеих сторон, результатом является четвертое тождество.

Три угла являются углами некоторого треугольника тогда и только тогда, когда их сумма равна 180 ° (π радиан). Какое условие на 12 углов необходимо и достаточно, чтобы они были 12 углами какого-нибудь тетраэдра? Ясно, что сумма углов любой стороны тетраэдра должна составлять 180 °. Так как таких треугольников четыре, существует четыре таких ограничения на суммы углов, и количество степеней свободы тем самым сокращается с 12 до 8. Четыре соотношения, задаваемые этим синусоидальным законом, дополнительно уменьшают число степеней свободы: от 8 до не 4, а 5, поскольку четвертое ограничение не является независимым от первых трех. Таким образом, пространство всех форм тетраэдров является 5-мерным.

Закон косинусов для тетраэдров

Пусть {P 1,P2, P 3, P 4 } – точки тетраэдра. Пусть Δ i – площадь грани, противоположная вершине P i, и пусть θ ij – двугранный угол между двумя гранями тетраэдра, примыкающими к ребру. P iPj.

Закон косинусов для этого тетраэдра, который связывает площади граней тетраэдра с двугранными углами вокруг вершины, задается следующим соотношением:

Δ i 2 = Δ j 2 + Δ К 2 + Δ l 2 – 2 (Δ j Δ k соз ⁡ θ il + Δ j Δ l cos ⁡ θ ik + Δ k Δ l cos ⁡ θ ij) { displaystyle Delta _ {i} ^ {2} = Delta _ {j} ^ {2} + Delta _ {k} ^ {2} + Delta _ {l} ^ {2} -2 ( Delta _ {j} Delta _ { k} cos theta _ {il} + Delta _ {j} Delta _ {l} cos theta _ {ik} + Delta _ {k} Delta _ {l} cos theta _ { ij})} $Delta _ {i} ^ {2} = Delta _ {j} ^ {2} + Delta _ {k} ^ {2} + Delta _ {l} ^ {2} -2 ( Delta _ {j} Дельта _ {k} cos theta _ {il} + Delta _ {j} Delta _ {l} cos theta _ {ik} + Delta _ {k} Delta _ {l} cos theta _ {ij})$

Внутренняя точка

Пусть P – любая внутренняя точка тетраэдра объема V, вершинами которого являются A, B, C и D, а площади противоположных граней – это F a, F b, F c и F d. Тогда

P A ⋅ F a + P B ⋅ F b + P C ⋅ F c + P D ⋅ F d ≥ 9 V. { displaystyle PA cdot F _ { mathrm {a}} + PB cdot F _ { mathrm {b}} + PC cdot F _ { mathrm {c}} + PD cdot F _ { mathrm {d}} geq 9V.} ${ displaystyle PA cdot F _ { mathrm {a}} + PB cdot F _ { mathrm {b}} + PC cdot F _ { mathrm {c }} + PD cdot F _ { mathrm {d}} geq 9V.}$

Для вершин A, B, C и D, внутренней точки P и футов J, K, L и M перпендикуляров от P к граням, и предположим, что грани имеют равные площади, тогда

PA + PB + PC + PD ≥ 3 (PJ + PK + PL + PM). { displaystyle PA + PB + PC + PD geq 3 (PJ + PK + PL + PM).}

Inradius

Обозначение внутреннего радиуса тетраэдра как r и inradii его треугольных граней как r i для i = 1, 2, 3, 4, мы имеем

1 r 1 2 + 1 r 2 2 + 1 r 3 2 + 1 r 4 2 ≤ 2 р 2, { displaystyle { frac {1} {r_ {1} ^ {2}}} + { frac {1} {r_ {2} ^ {2}}} + { frac {1} { r_ {3} ^ {2}}} + { frac {1} {r_ {4} ^ {2}}} leq { frac {2} {r ^ {2}}},} ${ frac {1} {r_ {1} ^ {2}}} + { frac {1} {r_ {2} ^ {2}}} + { frac {1} {r_ {3} ^ {2}}} + { frac {1} {r_ {4} ^ {2}}} leq { frac {2} {r ^ {2}}},$

с равенство тогда и только тогда, когда тетраэдр правильный.

Если A 1, A 2, A 3 и A 4 обозначают площадь каждой грани, значение r определяется как

r = 3 VA 1 + A 2 + A 3 + A 4 { displaystyle r = { frac {3V} {A_ {1} + A_ {2} + A_ {3} + A_ {4}}}} ${ displaystyle r = { frac {3V} {A_ {1} + A_ {2} + A_ {3} + A_ {4}}}}$

Эта формула получается из деления тетраэдра на четыре тетраэдра, точки которых являются тремя точками одной из исходных граней и центром. Поскольку четыре субтетраэдра заполняют объем, мы имеем V = 1 3 A 1 r + 1 3 A 2 r + 1 3 A 3 r + 1 3 A 4 r { displaystyle V = { frac {1} { 3}} A_ {1} r + { frac {1} {3}} A_ {2} r + { frac {1} {3}} A_ {3} r + { frac {1} {3}} A_ { 4} r} ${ displaystyle V = { frac {1} {3}} A_ {1} r + { frac {1} {3}} A_ {2} r + { frac {1} {3} } A_ {3} r + { frac {1} {3}} A_ {4} r}$ .

Окружной радиус

Обозначим радиус описанной окружности тетраэдра как R. Пусть a, b, c – длины трех ребер, которые встречаются в вершине, а A, B, C – длина противоположных краев. Пусть V – объем тетраэдра. Тогда

R = (a A + b B + c C) (a A + b B – c C) (a A – b B + c C) (- a A + b B + c C) 24 В. { displaystyle R = { frac { sqrt {(aA + bB + cC) (aA + bB-cC) (aA-bB + cC) (- aA + bB + cC)}} {24V}}.} ${ displaystyle R = { frac { sqrt {(aA + bB + cC) (aA + bB-cC) (aA-bB + cC) (- aA + bB + cC)}} {24V}}.}$

Центр описанной окружности

Центр описанной окружности тетраэдра может быть найден как пересечение трех биссектрисных плоскостей. Биссектрисная плоскость определяется как плоскость с центром и ортогональна ребру тетраэдра. С помощью этого определения центр описанной окружности C тетраэдра с вершинами x 0,x1,x2,x3может быть сформулирован как произведение матрица-вектор:

C = A – 1 B, где A = ([x 1 – x 0] T [x 2 – x 0] T [x 3 – x 0] T) и B = 1 2 (x 1 2 – x 0 2 x 2 2 – x 0 2 x 3 2 – x 0 2) { displaystyle { begin {align} C = A ^ {- 1} B { text {where}} A = left ({ begin {matrix} left [x_ {1} -x_ {0} right] ^ {T} \ left [x_ {2} -x_ {0} right] ^ {T} \ left [x_ {3} -x_ {0} right] ^ {T} end {matrix}} right) { text {and}} B = { frac {1} {2}} left ({ begin {matrix} x_ {1} ^ {2} -x_ {0} ^ {2} x_ {2} ^ {2} -x_ {0} ^ {2} \ x_ {3} ^ {2} -x_ {0} ^ {2} end {matrix}} right) \ конец {align}}} ${ displaystyle { begin {align} C = A ^ {- 1} B { text {where}} A = left ({ begin {matrix} left [x_ {1} -x_ {0} right] ^ {T} \ left [x_ {2} -x_ {0} right] ^ {T} \ left [x_ {3} -x_ { 0} right] ^ {T} end {matrix}} right) { text {and}} B = { frac {1} {2}} left ({ begin {matrix } x_ {1} ^ {2} -x_ {0} ^ {2} \ x_ {2} ^ {2} -x_ {0} ^ {2} \ x_ {3} ^ {2} -x_ { 0} ^ {2} end {matrix}} right) \ end {align}}}$

В отличие от центроида, центр описанной окружности не всегда может лежать внутри тетраэдра. Аналогично тупому треугольнику, у тупого тетраэдра центр описанной окружности находится вне объекта.

Центроид

Центр масс тетраэдра вычисляется как среднее арифметическое его четырех вершин, см. Центроид.

Грани

сумма площадей любых трех граней больше, чем площадь четвертой грани.

Целочисленные тетраэдры

Существуют тетраэдры, имеющие целочисленные длины ребер, площади граней и объем. Они называются тетраэдрами Герона. В одном примере один край 896, противоположный край 990 и четыре других края 1073; две грани – это равнобедренные треугольники с площадью 436800, а две другие – равнобедренные с площадью 47120, а объем равен 124185600.

Тетраэдр может иметь целочисленный объем и последовательные целые числа в качестве ребер, примером является тот, у которого есть ребра 6, 7, 8, 9, 10 и 11 и объем 48.

Родственные многогранники и соединения

Правильный тетраэдр можно рассматривать как треугольник пирамида.

Правильные пирамиды
Дигональ	Треугольник	Квадрат	Пятиугольник	Шестиугольник	Шестиугольник	Восьмиугольник	Эннеагональ	Десятиугольник…
Неправильный	Правильный	Равносторонний	Равнобедренный

Правильный тетраэдр можно рассматривать как вырожденный многогранник, равномерный двугранный антипризма, где базовые многоугольники редуцированы двуугольники.

Семейство однородных n-угольных антипризм [

]

Изображение многогранника

…

Апейрогональная антипризма

Сферическая мозаичное изображение

Плоское мозаичное изображение

Vertex con конфигурация n.3.3.3

2.3.3.3

3.3.3.3

4.3.3.3

5.3.3.3

6.3.3.3

7.3.3.3

8.3. 3.3

9.3.3.3

10.3.3.3

11.3.3.3

12.3.3.3

…

∞.3.3.3

Правильный тетраэдр можно рассматривать как вырожденный многогранник, равномерный двойственный двояковыпуклый трапецоэдр, содержащий 6 вершин, в двух наборах коллинеарных ребер.

Семейство n-угольных трапеций
Изображение многогранника										…	Апейрогональный трапецоэдр
Сферическое мозаичное изображение										Плоское мозаичное изображение
Конфигурация лица Vn.3.3.3	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	V7.3.3.3	V8.3.3.3	V10.3.3.3	V12.3.3.3	…	V∞.3.3.3

Применен процесс усечения к тетраэдру образует серию однородных многогранников. Усечение ребер до точек дает октаэдр как выпрямленный тетраэдр. Процесс завершается двунаправленной связью, уменьшая исходные грани до точек и снова создавая самодвойственный тетраэдр.

Семейство однородных тетраэдрических многогранников
Симметрия : [3,3], (* 332)	[3,3], (332)


{3,3}	t {3,3}	r {3,3}	t {3,3}	{3,3}	rr {3,3}	tr {3,3}	sr {3,3}
Двойники к однородным многогранникам

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Этот многогранник топологически связан как часть последовательности правильных многогранников с символами Шлефли {3, n}, продолжение в гиперболической плоскости.

* n32 мутация симметрии регулярных мозаик: {3, n} [ v ]
Сферический	Евклид.	Компактный гипер.	Парако.	Некомпактный гиперболический

3.3	3	3	3	3	3	3	3	3	3	3	3

* n32 мутация симметрии регулярных мозаик: {3, n} [

]

Сферический

Евклид.

Компактный гипер.

Парако.

Некомпактный гиперболический

3.3

Тетраэдр топологически связан с серией правильных многогранников и мозаик с фигурами вершин порядка 3 .

* n32 изменение симметрии правильных мозаик: {n, 3} [ v ]
Сферическое	Евклидово	Компактное гиперболическое.	Парако.	Некомпактный гиперболический

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞, 3}	{12i, 3}	{9i, 3}	{6i, 3}	{3i, 3}

* n32 изменение симметрии правильных мозаик: {n, 3} [

]

Сферическое

Евклидово

Компактное гиперболическое.

Парако.

Некомпактный гиперболический

{2,3}

{3,3}

{4,3}

{5,3}

{6,3}

{7,3}

{8,3}

{∞, 3}

{12i, 3}

{9i, 3}

{6i, 3}

{3i, 3}

Соединения тетраэдров
Два тетраэдра в кубе
Соединение пяти тетраэдров
Соединение десяти тетраэдров

Можно построить интересный многогранник из пяти пересекающихся тетраэдров. Это соединение пяти тетраэдров было известно сотни лет. Это регулярно встречается в мире оригами. Соединение двадцати вершин даст правильный додекаэдр. Существуют как левосторонние, так и правосторонние формы, которые являются зеркальным отображением друг друга. Наложение обеих форм дает соединение десяти тетраэдров, в котором десять тетраэдров расположены как пять пар stellae octangulae. Октангула стелла представляет собой соединение двух тетраэдров в двойном положении, и его восемь вершин определяют куб как их выпуклую оболочку.

квадратный осоэдр – это еще один многогранник с четырьмя гранями, но у него нет треугольных граней.

Приложения

Численный анализ

Неправильный объем в пространстве можно аппроксимировать нерегулярной триангулированной поверхностью и нерегулярными тетраэдрическими элементами объема.

В численном анализе сложные трехмерные формы обычно разбиваются или аппроксимируются с помощью многоугольной сетки неправильных тетраэдров в процессе создания уравнений для конечно-элементный анализ, особенно в численном решении уравнений в частных производных. Эти методы имеют широкое практическое применение в вычислительной гидродинамике, аэродинамике, электромагнитных полях, гражданском строительстве, химической инженерии., военно-морская архитектура и инженерия и смежные области.

Химия

Ион аммония тетраэдрический

Форма тетраэдра наблюдается в природе в ковалентно связанных молекулах. Все sp-гибридизированные атомы окружены атомами (или неподеленными электронными парами ) в четырех углах тетраэдра. Например, в молекуле метана (CH. 4) или ионе аммония (NH. 4) четыре атома водорода окружают центральный атом углерода или азота с тетраэдрической симметрией. По этой причине один из ведущих журналов по органической химии называется Tetrahedron. Центральный угол между любыми двумя вершинами идеального тетраэдра равен arccos (−1/3), или приблизительно 109,47 °.

Вода, H. 2O, также имеет тетраэдрическую структуру., с двумя атомами водорода и двумя неподеленными парами электронов вокруг центральных атомов кислорода. Однако его тетраэдрическая симметрия не идеальна, поскольку неподеленные пары отталкиваются сильнее, чем одинарные связи O – H.

Четвертичные фазовые диаграммы в химии представлены графически в виде тетраэдров.

Однако четвертичные фазовые диаграммы в технике связи представлены графически на двухмерной плоскости.

Электричество и электроника

Если шесть одинаковых резисторов спаяны вместе, чтобы образовать тетраэдр, то сопротивление, измеренное между любыми двумя вершинами, будет вдвое меньше. одного резистора.

Поскольку кремний является наиболее распространенным полупроводником, используемым в твердотельной электронике, а кремний имеет валентность из четырех, тетраэдрическая форма четырех химических связей в кремнии сильно влияет на то, как кристаллы кремния образуются и какие формы они принимают.

Игры

4-сторонние игральные кости

В Королевскую игру Ура, датируемую 2600 годом до нашей эры, играли с набором четырехгранных игральных костей.

Особенно в ролевой игре, это твердое тело известно как 4-сторонний кубик, один из наиболее распространенных многогранных кубиков с номером свернувшись, появляясь вокруг нижней или верхней вершины. Некоторые головоломки, подобные кубику Рубика, являются тетраэдрическими, например, Pyraminx и Pyramorphix.

Color space

Тетраэдры используются в алгоритмах преобразования цветового пространства. для случаев, когда ось яркости по диагонали сегментирует цветовое пространство (например, RGB, CMY).

Современное искусство

Австрийская художница Мартина Шеттина создала тетраэдр, используя люминесцентные лампы. Он был показан на биеннале светового искусства в Австрии 2010.

Он используется в качестве обложки альбома в окружении черного пламени на The End of All Things to Come от Mudvayne.

Геология

Тетраэдрическая гипотеза, первоначально опубликованная Уильямом Лоутианом Грином для объяснения формирования Земли, была популярна в начале 20 века..

Структурная инженерия

Тетраэдр с жесткими краями по своей природе жесткий. По этой причине его часто используют для усиления рамных конструкций, таких как космические рамки.

авиация

. На некоторых аэродромах большой каркас в форме тетраэдра с двумя закрытыми сторонами из тонкого материала устанавливается на вращающийся стержень и всегда направлен против ветра. Он достаточно большой, чтобы его можно было увидеть с воздуха, и иногда он подсвечивается. Его цель – служить ссылкой для пилотов, указывающих направление ветра.

Тетраэдрический граф

Тетраэдрический граф

Вершины	4
Ребра	6
Радиус	1
Диаметр	1
Обхват	3
Автоморфизмы	24
Хроматическое число	4
Свойства	Гамильтониан, правильный, симметричный, дистанционно-регулярный, дистанционно-транзитивный, 3-вершинно-связанный, планарный граф
Таблица графов и параметров

скелет тетраэдра (содержащий вершины и ребра) образует граф с 4 вершинами и 6 ребрами. Это частный случай полного графа, K 4 и колесного графа, W 4. Это один из 5 платоновых графов, каждый из которых является скелетом своего платонового тела.

. 3-кратной симметрии

См. Также

спираль Бурдейка – Кокстера
Конфигурация Мёбиуса
Caltrop
Демигиперкуб и симплекс – n-мерные аналоги
Пентахорон – 4-мерный аналог
Tetra Pak
Тетраэдрический воздушный змей
Тетраэдрическое число
Упаковка тетраэдра
Треугольная дипирамида – построена путем соединения двух тетраэдров вдоль одной грани
Треугольный тетраэдр

Ссылки

Внешние ссылки

На Викискладе есть материалы, связанные с Тетраэдр .

Вайсштейн, Эрик У. «Тетраэдр». MathWorld.
Бесплатные бумажные модели тетраэдра и многих других многогранников
Удивительный, заполняющий пространство, нерегулярный тетраэдр, который также включает описание «вращающегося кольца тетраэдров», также известного как a калейдоцикл.

v t Фундаментальный выпуклый правильный и равномерный многогранник в измерениях 2–10
An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Треугольник	Квадрат	p -угольник	Шестиугольник	Пентагон
Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
5-элементный	16 ячеек • Tesseract	Demitesseract	24-элементный	120-элементный • 600-элементный
5-симплексный	5-ортоплекс • 5-куб	5-полукуб
6-симплекс	6-ортоплекс • 6-куб	6-полукуб	122 • 221
7-симплекс	7-ортоплекс • 7-куб	7-полукуб	132 • 231 • 321
8-симплекс	8-ортоплекс • 8-куб	8-полукуб	142 • 241 • 421
9-симплекс	9-ортоплекс • 9-куб	9-демикуб
10-симплекс	10-ортоплекс • 10-куб	10-полукуб
n-симплекс	n-ортоплекс • n- куб	n-полукуб	1k2 • 2k1 • k21	n-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

Источник

Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)

Задача

Длина ребра

Угол между ребрами

Угол между ребром и гранью. Векторное произведение

Площадь грани

Объем пирамиды. Смешанное произведение векторов

Уравнение прямой в пространстве

Уравнение плоскости

Уравнение высоты, опущенной на грань

Trigonometric quantities[edit]

Classical trigonometric quantities[edit]

Area and volume[edit]

Basic statements of trigonometry[edit]

Affine triangle[edit]

Projective triangle[edit]

Laws of trigonometry for the tetrahedron[edit]

Alternating sines theorem[edit]

The space of all shapes of tetrahedra[edit]

Law of sines for the tetrahedron[edit]

Law of cosines for the tetrahedron[edit]

Relationship between dihedral angles of tetrahedron[edit]

Skew distances between edges of tetrahedron[edit]

References[edit]

Содержание

Правильный тетраэдр

Координаты правильного тетраэдра

Углы и расстояния

Изометрии правильного тетраэдра

Ортогонально проекции правильного тетраэдра

Поперечное сечение правильного тетраэдра

Сферическая мозаика

Спиральное наложение

Другие особые случаи

Изометрии неправильных тетраэдров

Общие свойства

Объем

Формула типа Герона для объема тетраэдра

Разделитель объема

Неевклидов объем

Расстояние между краями

Свойства, аналогичные свойствам треугольника

Геометрические соотношения

Закон синусов для тетраэдров и пространства всех форм тетраэдров

Закон косинусов для тетраэдров

Внутренняя точка

Inradius

Окружной радиус

Центр описанной окружности

Центроид

Грани

Целочисленные тетраэдры

Родственные многогранники и соединения

Приложения

Численный анализ

Химия

Электричество и электроника

Игры

Color space

Современное искусство

Популярная культура

Геология

Структурная инженерия

авиация

Тетраэдрический граф

См. Также

Ссылки

Внешние ссылки

Чему равны углы между ребрами и гранями правильной пирамиды (тетраэдра)?

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://www.genon.ru/img/pohozhie-voprosy.png" width="19" height="19" alt />Популярные ответы

Оставить отзыв

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://www.genon.ru/img/pohozhie-voprosy.png" width="19" height="19" alt />Похожие вопросы

Вам также может понравиться

Как найти песню когда забыл название

Как найти андроид без симки потерянный телефон

Как составить письмо для спама

Добавить комментарий Отменить ответ

Популярные ответы

Похожие вопросы