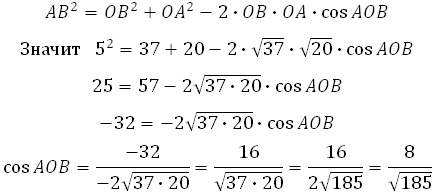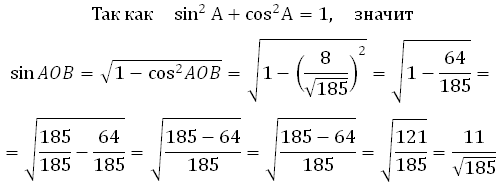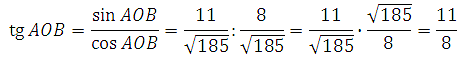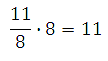СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Многоугольники: вычисление длин и углов
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д4 № 27449
i
Найдите косинус угла
В ответе укажите значение косинуса, умноженное на
Аналоги к заданию № 27450: 27449 26065 316033 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
2
Задания Д4 № 27450
i
На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите тангенс этого угла.
Аналоги к заданию № 27450: 27449 26065 316033 … Все
Решение
·
Видеокурс
·
Помощь
3
Задания Д4 № 27451
Найдите синус угла
В ответе укажите значение синуса, умноженное на
Аналоги к заданию № 27451: 27452 27453 510060 Все
Решение
·
Видеокурс
·
Помощь
4
Задания Д4 № 27456
i
На клетчатой бумаге с размером клетки 1
1 изображён угол. Найдите тангенс этого угла.
Аналоги к заданию № 27456: 26074 26077 26080 … Все
Источник: Пробный ЕГЭ по профильной математике Санкт-Петербург 05.04.2016. Вариант 1
Решение
·
2 комментария
·
Видеокурс
·
Помощь
5
Задания Д4 № 27459
i
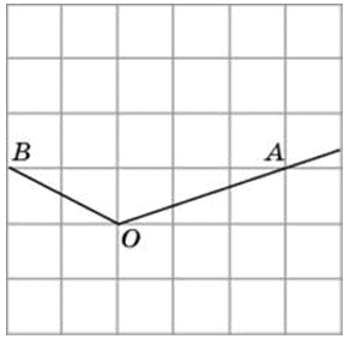
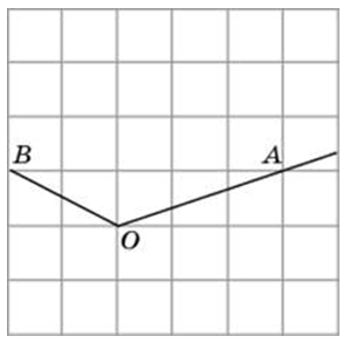
Найдите тангенс угла AOB. Сторона одной клетки равна 1.
Аналоги к заданию № 27459: 27457 27458 Все
Решение
·
Видеокурс
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.
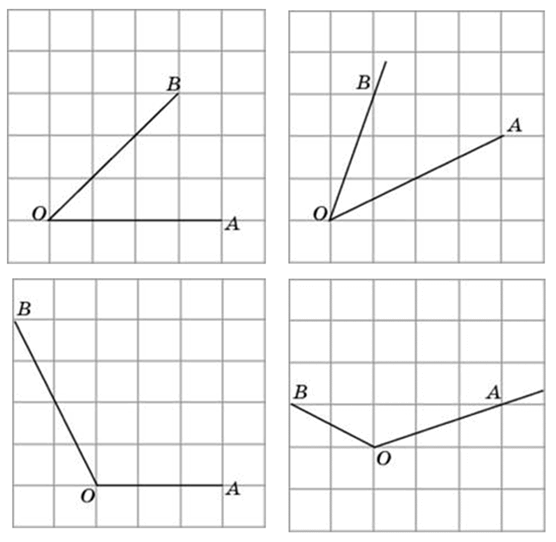
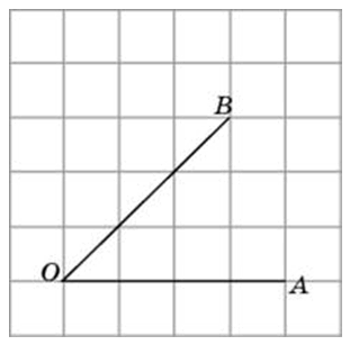
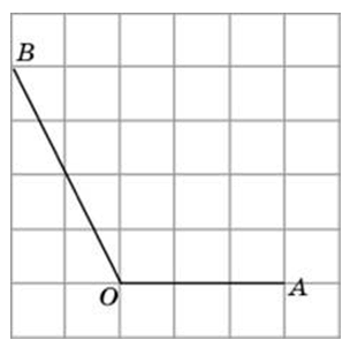
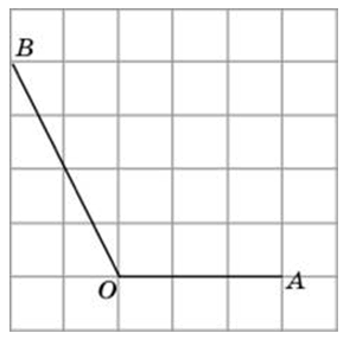
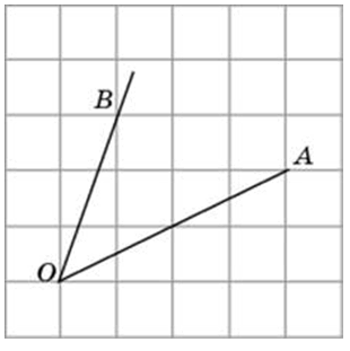
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):
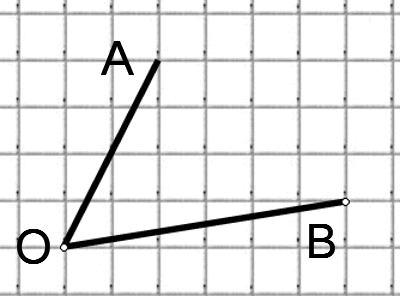
Итак, рассмотрим задание:
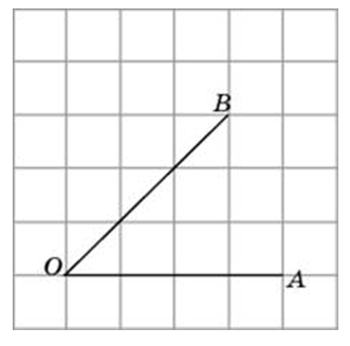
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.
Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).
АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,
ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,
OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Из основного тригонометрического тождества можем найти sin AOB:
*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.
Теперь можем найти тангенс:
Умножим результат на 8 и запишем ответ:
Ответ: 11
Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.
Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.
Посмотреть решение
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях )
Один из типов задач в задании 3 – это задачи на нахождение углов.
На клетчатой решетке изображен угол, величину которого надо найти.
Это могут быть самые разнообразные углы:
Методы вычисления могут быть разные.
Принцип большинства заданий – найти прямоугольный треугольник и вычислить у него стороны и найти угол используя синус или косинус или тангенс (в зависимости от задания)
Если необходимо найти тангенс тупого угла, то в начале находим тангенс смежного острого угла и применяем формулу приведения (в ответе появится минус). Напомню, что синус тупого и острого угла имеет один и тот же знак, а вот косинус, так же как и тангенс, тупого и острого угла имеет противоположные знаки.
Если так не получается, то начинаем искать отрезки, треугольники и вычислять стороны. Применять свойство равнобедренных треугольников или теорему косинусов.
Если совсем непонятно, что делать, то встройте угол в прямоугольник и посчитайте все стороны и решение придет
Мы рассмотрели один из типов задач. Главное, поймите принцип, а тогда решите любую задачу.
Чтобы найти косинус угла по клеточкам, следует вспомнить, что это собственно за величина – косинус.
По определению, косинус – это отношение прилежащего катета к гипотенузе.
Зная это определение мы очень легко можем найти косинус любого прямоугольного треугольника, нарисованного на клеточках. То есть если задан просто угол, мы достраиваем его до прямоугольного треугольника:
Разберем несколько случаев.
Катеты расположены вертикально и горизонтально. Тогда их длину определяем по клеточкам, а длину гипотенузы по теореме Пифагора.
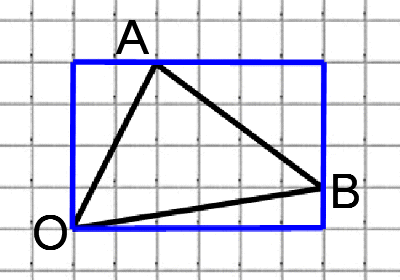
Катеты расположены произвольно. Заключаем треугольник в прямоугольник и находим катеты и гипотенузу по теореме Пифагора для всех трех сторон. Дальше находим косинус как отношение по определению.
Например здесь катет АО находится как корень из 20 (16+4). Гипотенуза ОВ находится как корень из 37 (36+1). Их отношение – косинус угла АОВ.
Если треугольник АОВ не получается прямоугольным, то имеет смысл использовать теорему косинусов:
юра фролов
Ученик
(58),
закрыт
8 лет назад
” />
Дополнен 8 лет назад

Тесты_математика
Гений
(51456)
8 лет назад
cos=–3/(3^2+4^2)=-3/5
Тоня БайгишиеваУченик (231)
8 лет назад
А почему –3 делят?
Тесты_математика
Гений
(51456)
потому что cos -это отношение прилежащего катета к гипотенузе а гипотенузу ищешь по теореме Пифагора я уже забыла про эту задачу так давно было он скоро должен быть уже на голосовании на ЛУЧШИЙ ОТВЕТ
Лариса Козина
Мудрец
(13373)
8 лет назад
Давай выполним дополнительные построения
1)продли влево горизонтальную прямую, 2)из верхнего конца наклонной опусти перпендикуляр
Слева у тебя получился прямоугольный треугольник
Теперь обозначим углы, прилежащие к горизонтальной прямой. Острый угол в треугольнике обозначим а, справа тупой угол обозначим в
Решение: cosb=cos(180-a)=-cosa
Гипотенуза в треугольнике по т Пифагора равна5
-cosa=-35=-0,6