Учебник
Геометрия, 10 класс
Угол между скрещивающимися прямыми в пространстве
Скрещивающиеся прямые – не параллельны, не имеют общих точек, не пересекаются.
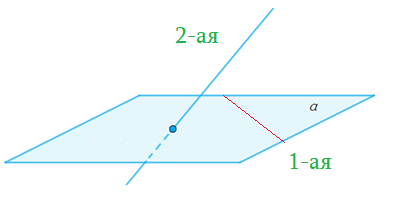
Признаки Скрещивающихся прямых
- 1-ая прямая лежит в плоскости, а 2-ая пересекает плоскость в точке не из 1-ой, то прямые скрещивающиеся.
- Через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой. Единственная.
- Скрещивающиеся $a$ и $b$ : есть пара пареллельных плоскостей $alpha$ и $beta$, таких что $ain alpha$, $bin beta$
Задача 1: В прямоугольном параллелепипеде $ABCDMNKL$ найти угол между
скрещивающимися прямыми $AN$ и $BK$, если известны ребра $BA=36$, $BN=15$, $BC=20$
- Как находить угол между двумя стереометрическими объектами? по алгоритму параллельных переносов, совмещений.
- Свойство инвариантности углов при параллельном переносе стереометрических объектов – прямых, плоскостей:
- Если объекты $A$ и $B$ параллельны соответственно $A’$ и $B’$, то углы между парами равные: $angle left(A;Bright)=angle left(A’;B’right)$
- В нашем случае, $BKparallel AL$, поэтому равны углы $angle left(AN;BKright)=angle left(AN;ALright)=angle NAL$
- Перетащим $BK$ по плоскости $BKLA$ вдоль $BA$ до совмещения с точкой $A$. Тогда $BK$ совметится с отрезком $AL$.
- Итак, мы ищем угол $angle NAL$. Найдем его через теорему косинусов в треугольнике $ANL$ для угла $angle NAL$ :
- *** $NL^2=AN^2+AL^2-2cdot ANcdot NLcdot cos angle NAL$
- Стороны $AN$, $NL$ и $AL$ можем признать диагоналями граней – прямоугольников, значит, найти их по теоремам Пифагора.
- Решение: $AN=sqrt{36^2+15^2}=39$ $AL=sqrt{20^2+15^2}=25$ $NL=sqrt{36^2+20^2}=4cdot sqrt{106}$
- Из теоремы косинусов $cos angle NAL=frac{AN^2+AL^2-NL^2}{2cdot ANcdot AL}=frac{39^2+25^2-16cdot 106}{2cdot 39cdot 25}=frac{450}{1950}=frac{3}{13}$ Ответ: $angle NAL=arccos frac{3}{13}$
- Признак: $NAL$ – плоскость угла: $ANin NAL$ и $BKparallel NAL$
case I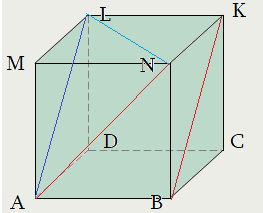 
case II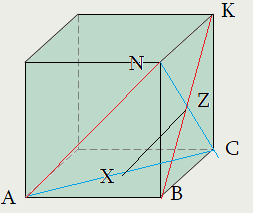 
Алгоритм: нахождение угла между прямыми путем параллельного переноса (демонстрация по II, прямые $AN$, $BK$ ):
1-ый шаг: Выбираем точку, в которой хотим совместить прямые. Например, точку $Z$ – середину отрезка $BK$.
2-ой шаг: Для прямой $AN$ определим плоскость “скольжения” – плоскость, содержащая эту прямую и точку $Z$. Это $ANC$
3-ий шаг: Двинем прямую $AN$ по плоскости $ANC$ оставаясь параллельно “как стержень”. Она совместится с отрезком $ZX$.
4-ый шаг: Что за точка $X$ ? угол $angle XZB$ – именно то, что нам нужно: $angle XZB=angle left(XZ;BKright)=angle left(AN;BKright)$.
Признак: – увидеть ту главную плоскость угла , которая параллельна обеим скрещивающимся прямым. Здесь это $XZB$.
Задача 2: В правильной треугольной призме все ребра 1. Найти косинус угла $angle left(AB;CMright)$
- $ABCMNK$ правильная призма: в основании правильный $bigtriangleup ABC$ , ребро $BN$ перпендикулярно основанию.
- Нужен угол между $AB$ и $CM$. Выберем Точкой совмещения $M$. Прямая $CM$ уже проходит через нее.
- Прямая $AB$ и точка $M$ лежат в плоскости $ABNM$. Значит, $ABNM$ – плоскость сколжения. $AB$ перейдет в $MN$.
- Путем параллельного совмещения $AB$ с $MN$ мы устоновили, что искомый угол – это $angle CMN$.
- Косинус угла $angle CMN$ можно найти по теореме косинусов треугольника $CMN$: $cos angle CMN=frac{CM^2+MN^2-CN^2}{2cdot CMcdot MN}$
- Признак: $CMN$ – плоскость угла: $ABparallel CMN$ и $MCin CMN$
k задачe 2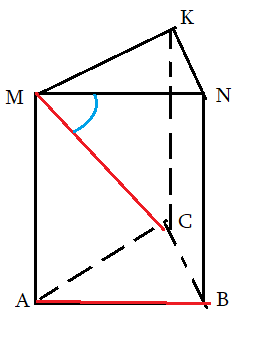 
к задаче 3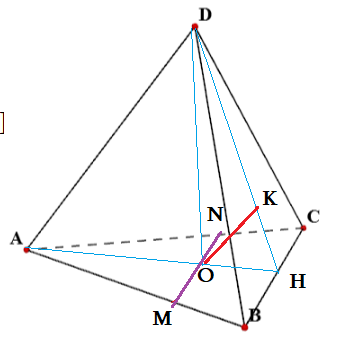 
Задача 3: В правильном тетраэдре $DABC$ все ребра 1 см. Найти угол между $AD$ и $BC$.
- Для нахождения угла, совместим “движениями” наши прямые в точку $O$ – основание высоты $DO$ .
- В правильном тетраэдре в основании равносторонный треугольник $DABC$, высота пирамиды попадает в центр окружностей.
- Точка $O$ – пересечение высот, медиан, биссектрис. $O$ лежит на высоте $AH$ , $DH$ – высота грани $BDC$.
- В точке $O$ проведем прямую параллельную прямой $BC$. Им будет линия $MN$
- В точке $O$ проведем прямую $OK$, параллельную $AD$. Она будет лежат в плоскости $ADH$ Значит, $Kin DH$.
- Итак, “взамен” наших $AD$ и $BC$ мы получили прямые $OK$ и $MN$ : $OKparallel AD$, $MNparallel BC$
- по свойству углов при параллельном переносе $angle left(AD;BCright)=angle left(OK;MNright)=angle MOK$
- Найти $angle MOK$ ? Легко! учтите, что у нас правильный тетраэдр и находите.
- Признак: $MONK$ – плоскость угла: $ADparallel MONK$ и $BCparallel MONK$
Алгоритм: вычисление угла в пространстве или плоскости
- В каком треугольнике этот угол? узнать стороны треугольника и найти угол по теореме косинусов.
- Если треугольник окажется равнобедренным, то провести высоту и найти угол прямоугольного треугольника.
- А если треугольник прямоугольный, то написать cos или sin или tg этого угла и найти как arc !
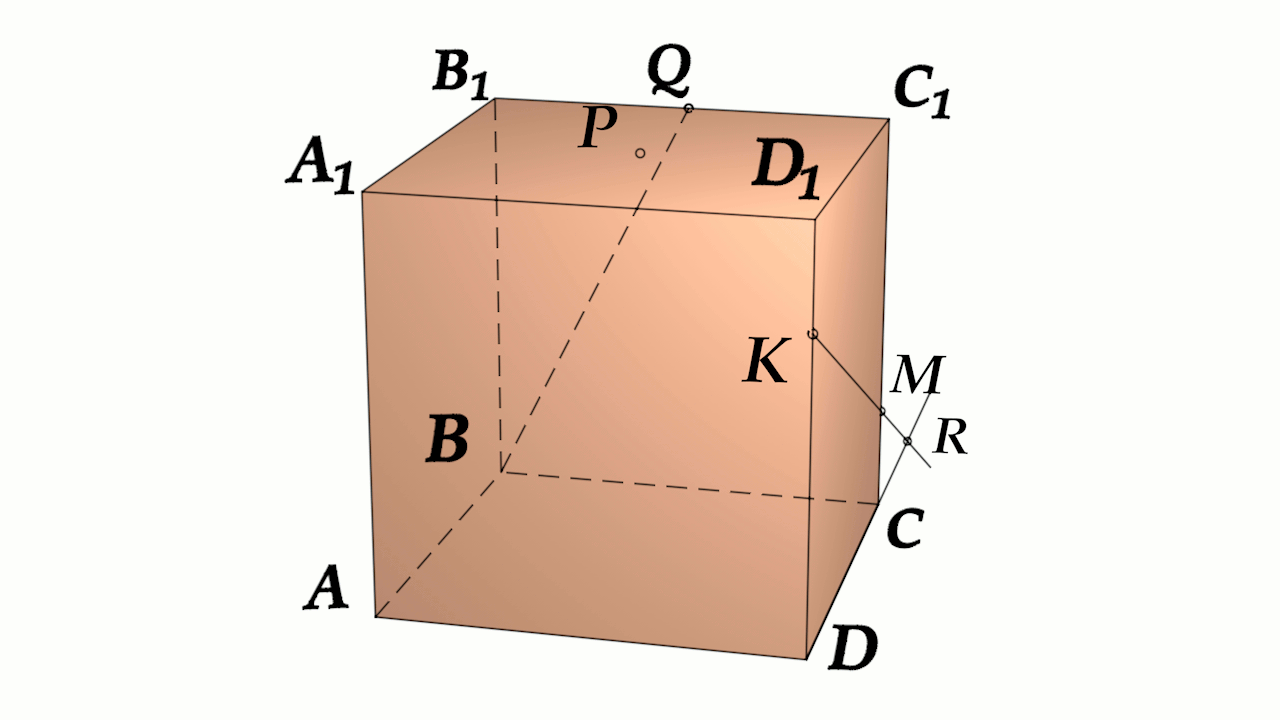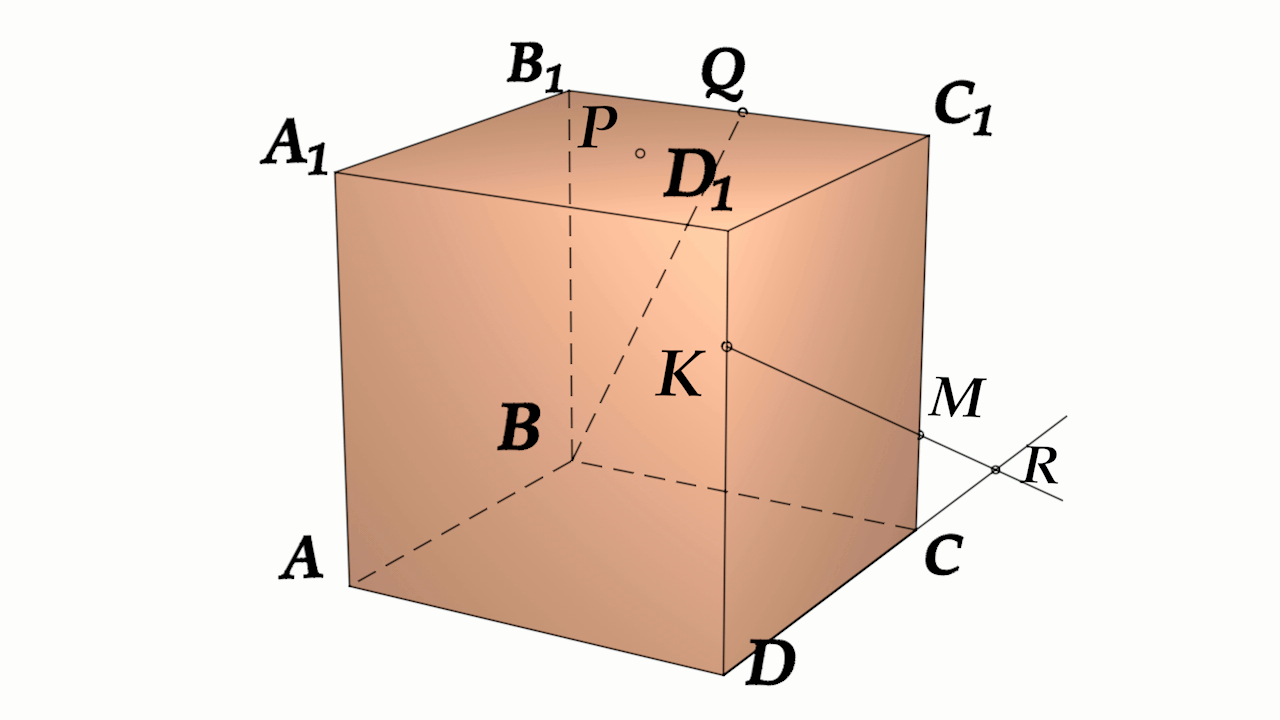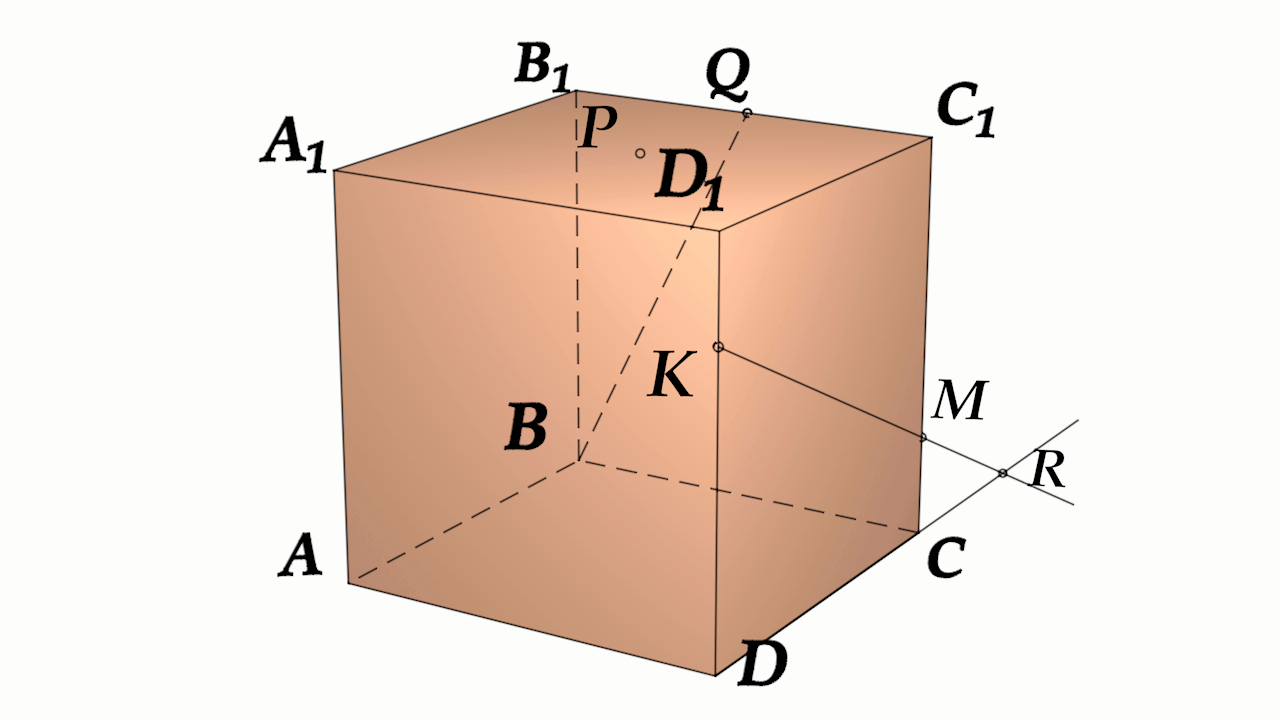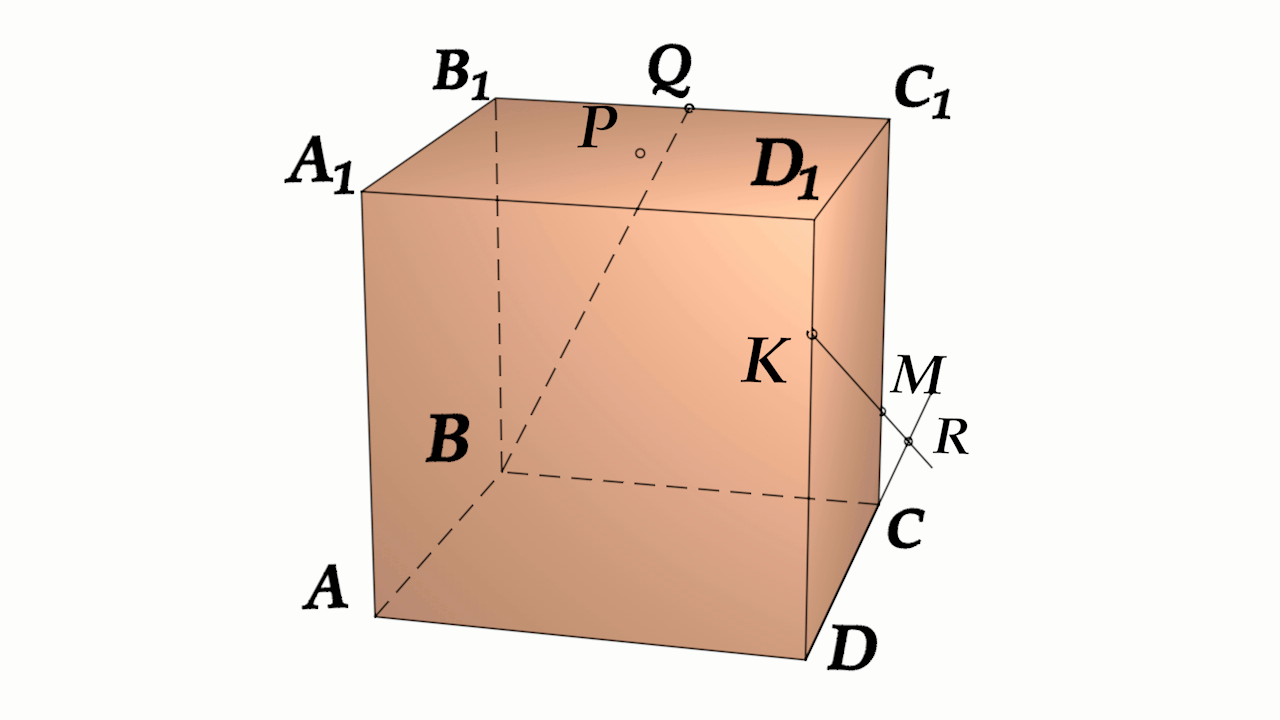
Задача 4: В кубе $ABCD{A_1}{B_1}{C_1}{D_1}$ все ребра равны 1. Точка $Q$ – середина ребра . Точка $K$
делит ребро $D_1D$ в соотношении 1 : 3 считая от вершины $D_1$, а точка $M$ делит $C_1C$ в соотношении
5 : 2 считая от вершины $C_1$. Найти угол между скрещивающимися прямыми $BQ$ и $KM$ .
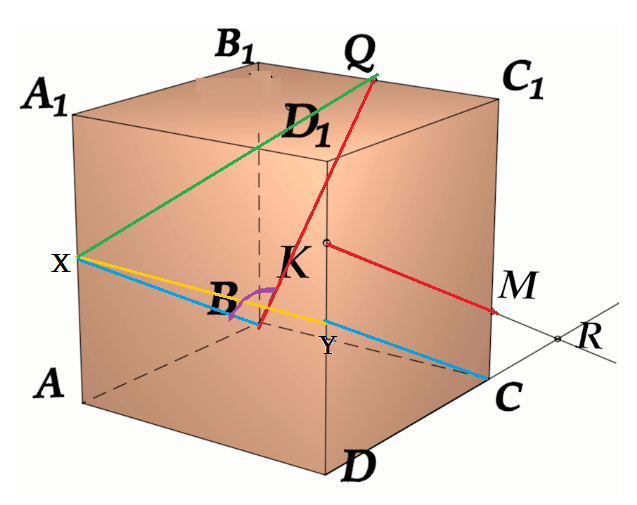
- Параллельными переносами добъемся совмещения в точке $B$. Для этого, перенесем $KM$ в два этапа.
- Сперва соскользим $KM$ по грани $DD_1C_1C$ вдоль $C_1C$ до вершины $C$. Получим отрезок $CYparallel MK$
- Затем, $CY$ протащим параллельно себе вдоль пути $CB$ и перейдем к отрезку $BXparallel CY$.
- В итоге получили то, что надо: $KM$ параллельна $BX$, потому как $MKparallel CYparallel BX$.
- Требуемый угол $angle left(MK;BQright)=angle left(BX;BQright)=angle XBQ$. Найдем его через треугольник $bigtriangleup XBQ$
- В теореме косинусов нам нужны стороны этого треугольника. Вычислим постепенно, шаг за шагом, зная ребро куба 1:
- Из отношения $frac{D_1K}{DK}=frac{1}{3}Rightarrow D_1K=frac{1}{4} DK=frac{3}{4}$. Из отношения $frac{C_1K}{CM}=frac{5}{2}Rightarrow C_1M=frac{5}{7} CM=frac{2}{7}$
- $MKparallel CYRightarrow KY=MC$ отрезок $DY=D_1D-D_1K-KY=1-frac{1}{4}-frac{2}{7}=frac{13}{28}$
- $BXparallel CYRightarrow BX=DY=frac{13}{28}$. По условию задачи $B_1Q=frac{1}{2}$.
- Нужные нам стороны треугольника $bigtriangleup XBQ$ являются гипотенузами прямоугольных треугольников.
- Зная все катеты, как части ребер, по теореме Пифагора найдем стороны $XB$, $BQ$, $XQ$.
- Нужный угол $angle XBQ$ вычислим из теоремы косинусов $XQ^2=XB^2+BQ^2-2cdot XBcdot BQcdot cos angle XBQ$
- наконец: $cos angle XBQ=frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$ $angle XBQ=arccos frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$
- Признак: $XBQ$ – плоскость угла: $KMparallel XBQ$ и $BQin XBQ$
Задача 5: В правильной треугольной призме $ABCMNK$ все ребра равны 2. Точка $D$ делит
ребро $MN$ в отношении 3 : 2 считая от вершины $M$. Найдите угол между прямыми $AD$ и $BK$.
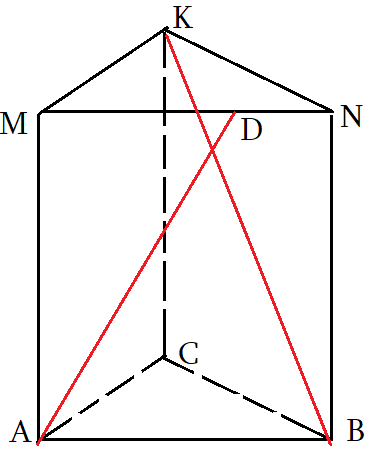
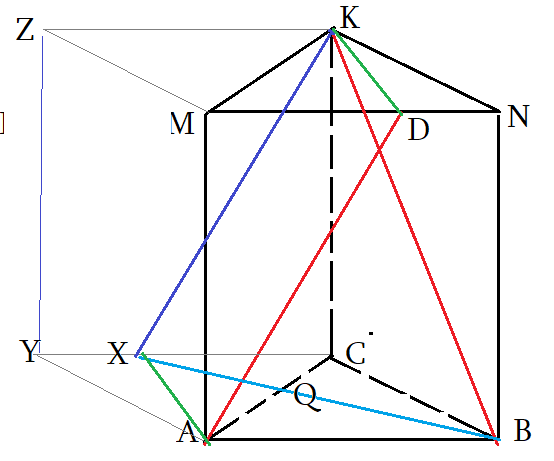
- Чтоб найти угол между скрещивающимися прямыми, нужно “подвигать параллельно” $AD$ и $BK$ до совмещения.
- Если двинуть $AD$ так, чтоб точка $D$ совпала с $K$ – т.е. скользить по плоскости $ADK$, но тогда другой конец $D$ вне рисунка.
- Достроим призму до параллелепипеда $ABCYMNKZ$ и все нужные отрезки, “движения”, плоскости будут внутри!
- $AD$ скользит по плоскости $ADK$ и совпадет с $XK$. Точка $X$, конечно, окажется на ребре $YC$
- по построению: $Xin CDK$ плоскости; $ADparallel XK$ , $XCparallel AB$ . Значит, $XK$ параллельна $AD$
- Угол между прямыми $angle left(AD;BKright)=angle left(XK;BKright)=angle XKB$. Надо найти угол $angle XKB$.
- Угол $XKB$ ищем , как обычно, через треугольник $bigtriangleup XKB$, с помощью теоремы косинусов.
- Для этого надо найти стороны этого треугольника. Сторону $BK$ найдем по Пифагору для треугольника $bigtriangleup BKC$.
- $XC=MD$, найдем $MD$ из отношения 3 : 2 для $MN$ . Затем, по Пифагору $bigtriangleup XKC$ найдем $XK$.
- С вычислением $XB$ придется повозится через теорему косинусов треугольника $bigtriangleup XBC$, две его стороны известны.
- А что с углом $angle XCB$? по условию $bigtriangleup ABC$ равносторонный, значит в параллелограмме $angle YCB=120$ градусов.
- Ну и финально: как только найдем все стороны $bigtriangleup XKB$, мы найдем и его угол $angle XKB$ – то что надо!
- Признак: $XKB$ – плоскость угла: $ADparallel XKB$ и $BKin XKB$
Упражнения:
Призма
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.
Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
$С_1Н$ – высота
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
$P_{осн}$ – периметр основания;
$S_{осн}$ – площадь основания;
$S_{бок}$ – площадь боковой поверхности;
$S_{п.п}$ – площадь полной поверхности;
$h$ – высота призмы.
$S_{бок}=P_{осн}·h$
$S_{п.п}=S_{бок}+2S_{осн}$
$V=S_{осн}·h$
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S={a·h_a}/{2}$, где $h_a$ – высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ – это полупериметр $p={a+b+c}/{2}$
- $S=p·r$, где $r$ – радиус вписанной окружности
- $S={a·b·c}/{4R}$, где $R$ – радиус описанной окружности
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ – катеты прямоугольного треугольника.
В основании лежит четырехугольник
1. Прямоугольник
$S=a·b$, где $а$ и $b$ – смежные стороны.
2. Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ – диагонали ромба
$S=a^2·sinα$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами.
3. Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции.
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
1. Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ – длина стороны.
2. Квадрат
$S=a^2$, где $а$ – сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
$S=6·S_{треугольника}={6·a^2√3}/{4}={3·a^2√3}/{2}$, где $а$ – сторона правильного шестиугольника.
Пример:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.
Решение:
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
$S_{п.п}=S_{бок}+2S_{осн}=P_{осн}·h+2S_{ромба}$
В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.
$АВ=√{5^2+12^2}=√{25+144}=√{169}=13$
$Р=13·4=52$
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
$S_{основания}={d_1·d_2}/{2}={10·24}/{2}=120$
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
$S_{п.п}=P_{осн}·h+2S_{ромба}=52·20+2·120=1040+240=1280$
Ответ: $1280$
Цилиндр – это та же призма, в основании которой лежит круг.
$S_{бок}=P_{осн}·h=2πRh$
$S_{п.п}=S_{бок}+2S_{осн}=2πRh+2πR^2=2πR(h+R)$
$V=S_{осн}·h=πR^2 h$
Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.
Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ – средняя линия, так как соединяет середины соседних сторон.
$MN {//} AC, MN = {AC}/{2}$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ – коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А: ВС$ – противолежащий катет; $АС$ – прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ – радиус описанной около треугольника окружности.
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$
Для решения рассмотрим рисунок (https://bit.ly/2GHxi4Y).
Прямые ВА1 и ДВ1 скрещивающиеся прямые. Проведем прямую ДЕ1, тогда угол Е1ДВ1 наш искомый угол. Проведем отрезок Е1В1.
Е1В1 большая диагональ шестиугольника которая равна диаметру описанной около него окружности, а так как радиус окружности равен длине стороны шестиугольника, то Е1В1 = 2 * АВ = 2 * 1 = 2 см.
В прямоугольном треугольнике ДЕЕ1, ДЕ12 = ДЕ2 + ЕЕ12 = 1 + 1 = 2. ДЕ1 = √2 см.
Треугольник Е1В1Д прямоугольный с прямым углов в точке Е1, тогда по теореме Пифагора, ДВ12 = ДЕ12 + Е1В12 = 2 + 2 = 4. ДВ1 = 2 см.
В треугольнике ДЕ1В1, по теореме косинусов, Е1В12 = ДЕ12 + ДВ12 – 2 * ДЕ1 * ДВ1 * CosЕ1ДВ1.
4 = 2 + 4 – 2 * √2 * 2 * CosЕ1ДВ1 = 6 – 4 * √2 * CosЕ1ДВ1.
4 * √2 * CosЕ1ДВ1 = 6 – 4 = 2.
CosЕ1ДВ1 = 1 / 2 * √2 = √2 / 4.
Ответ: Косинус угла равен √2 / 4.
Светило науки – 1549 ответов – 6854 помощи
Ответ:
Косинус угла между диагональю боковой грани и другой боковой гранью призмы равен 0,54.
Объяснение:
4. Длина ребра основания правильной треугольной призмы равна 4 см, а ее высота – 1 см. Найдите косинус угла между диагональю боковой грани и другой боковой гранью призмы.
Дано: АВСА₁В₁С₁ – правильная треугольная призма;
АВ = 4 см; АА₁ = 1 см;
В₁С – диагональ;
Найти: косинус угла между В₁С и (АВ₁В).
Решение:
- В правильной треугольной призме основания – равносторонние треугольники, а боковые грани – равные прямоугольники.
Определимся с углом.
- Углом между прямой и плоскостью называют угол между прямой и ее проекцией на эту плоскость.
Из точки опустим перпендикуляр СН на плоскость (АВ₁В).
В₁Н – проекция В₁С на плоскость (АВ₁В).
⇒ ∠НВ₁С – искомый угол.
Обозначим этот угол α.
- Косинус угла – отношение прилежащего катета к гипотенузе.
Найдем В₁С.
Рассмотрим ΔВ₁ВС – прямоугольный.
По теореме Пифагора найдем В₁С:
В₁С² = ВВ₁² + ВС² = 1 + 16 = 17 ⇒ В₁С = √17 (см)
Найдем В₁Н.
Рассмотрим ΔНВ₁В – прямоугольный.
СН – высота ΔАВС – равностороннего.
- В равностороннем треугольнике высоты являются медианами.
⇒ АН = НВ = 4 : 2 = 2 (см)
По теореме Пифагора найдем В₁Н:
В₁Н² = В₁В² + НВ² = 1 + 4 = 5 ⇒ В₁Н = √5 (см).
#SPJ1
По условию задачи в правильной треугольной призме (displaystyle ABCA_1B_1C_1) требуется найти косинус угла между прямыми (displaystyle AD) и (displaystyle BE small, ) где (displaystyle D) и (displaystyle E) – середины рёбер соответственно (displaystyle A_1B_1) и (displaystyle B_1C_1 small. )
Данные прямые являются скрещивающимися.
Определение
Угол между скрещивающимися прямыми
Угол между скрещивающимися прямыми – это угол между прямыми, параллельными заданным и лежащими в одной плоскости.
Замечание / комментарий
Для построения угла проще всего выбрать точку пространства и через нее провести две прямые, параллельные исходным. Угол между этими прямыми и будет искомым углом.
На прямой (displaystyle BE) выберем точку (displaystyle E small. )
Через точку (displaystyle E) построим прямую (displaystyle EMsmall, ) параллельную прямой (displaystyle AD small. )
Угол между скрещивающимися прямыми (displaystyle AD) и (displaystyle BE) равен углу между пересекающимися прямыми (displaystyle EM) и (displaystyle BE small. ) Для того, чтобы найти косинус угла между прямыми (displaystyle AD) и (displaystyle BE small, ) необходимо вычислить (displaystyle cos angle BEM small. )
Соединим отрезком точки (displaystyle B) и (displaystyle M) и рассмотрим треугольник (displaystyle BEM small. )
По теореме косинусов
(displaystyle BM^2=BE^2+EM^2-2 cdot BE cdot EM cdot cos angle BEM small. )
Выразим косинус угла (displaystyle BEM small: )
(displaystyle cos angle BEM=frac{BE^2+EM^2-BM^2}{2 cdot BE cdot EM} small.)
Чтобы вычислить (displaystyle cos angle BEMsmall,) необходимо найти длины отрезков (displaystyle BEsmall, ) (displaystyle EM) и (displaystyle BM small. )
(displaystyle BE=frac{sqrt{5}}{2} small. )
(displaystyle EM=frac{sqrt{5}}{2} small. )
(displaystyle BM=frac{sqrt{3}}{2} small. )
Подставим найденные значения (displaystyle BE=frac{sqrt{5}}{2} small, ) (displaystyle EM=frac{sqrt{5}}{2} small, ) (displaystyle BM=frac{sqrt{3}}{2} ) и вычислим косинус угла (displaystyle BEM small: )
(displaystyle cos angle BEM=frac{BE^2+EM^2-BM^2}{2 cdot BE cdot EM} small, \ )
(displaystyle cos angle BEM=frac{bigg( frac{sqrt{5}}{2} bigg)^2+bigg( frac{sqrt{5}}{2} bigg)^2-bigg( frac{sqrt{3}}{2} bigg)^2}{2 cdot frac{sqrt{5}}{2} cdot frac{sqrt{5}}{2} } small,\ )
(displaystyle cos angle BEM=frac{frac{5}{4}+frac{5}{4}-frac{3}{4}}{frac{5}{2}}=frac{7}{4}:frac{5}{2}=frac{7 cdot 2}{4 cdot 5}=frac{7}{10}=0{,}7 small. )
Ответ: (displaystyle 0{,}7 small. )
