В данной публикации мы рассмотрим, что такое угол меду двумя векторами, и приведем формулу, с помощью которой можно найти его косинус. Также разберем пример решения задачи по этой теме.
- Нахождение угла между векторами
- Пример задачи
Нахождение угла между векторами
Угол между двумя векторами, берущими начало в одной и той же точке – это наименьший угол, на который можно повернуть один из данных векторов вокруг своей начальной точки до положения, при котором он будет сонаправлен со вторым вектором.
Косинус угла между двумя векторами равняется скалярному произведению векторов, разделенному на произведение длин (модулей) этих векторов.
Для расчета косинуса угла используется формула ниже:
Пример задачи
Найдем угол между векторами a = {4; 3} и b = {12; 5}.
Решение
1. Для начала рассчитаем их скалярное произведение:
a · b = 4 · 12 + 3 · 5 = 48 + 15 = 63.
2. Теперь найдем длины (модули) заданных векторов:
3. Применим формулу для нахождения косинуса угла:
4. Следовательно, угол приблизительно равняется 14,26° (arccos 0,9692).
Косинус угла между векторами
Формула
Чтобы найти косинус угла между векторами нужно найти отношение скалярного произведения векторов и произведение их длин (модулей). Если векторы заданы на плоскости двумя координатами $ overline{a}=(x_1;y_1) $ и $ overline{b}=(x_2;y_2) $, то косинус угла между ними вычисляется по формуле:
$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}|cdot |overline{b}|} = frac{x_1 x_2 + y_1 y_2}{sqrt{x_1 ^2 + y_1 ^2}cdot sqrt{x_2 ^2 + y_2 ^2}} $$
Если векторы будут заданы тремя координатами $ overline{a}=(x_1;y_1;z_1) $ и $ overline{b}=(x_2;y_2;z_2) $, то есть в пространстве, то нахождение косинуса угла между векторами нужно выполнить по формуле:
$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}|cdot |overline{b}|} = frac{x_1 x_2 + y_1 y_2 + z_1 z_2}{sqrt{x_1 ^2 + y_1 ^2 +z_1 ^2}cdot sqrt{x_2 ^2 + y_2 ^2 + z_2 ^2}} $$
В числителе находится скалярное произведение векторов, то есть каждая координата умножается на соответствующую координату другого вектора и при этом находится сумма всех произведений. А в знаменателе расположено произведение модулей векторов. Каждый модуль равен извлеченному квадратному корню из суммы квадратов координат вектора.
Примеры решений
| Пример |
| Даны два вектора $ overline{a} =(3;1) $ и $ overline{b} = (2;4) $. Требуется найти косинус угла между векторами. |
| Решение |
|
Напомним как найти косинус угла между векторами. Необходимо определить на плоскости или в пространстве находятся векторы, то есть сколько у них координат. Затем воспользоваться подходящей формулой. Первым делом вычисляем скалярное произведение: каждую координату одного вектора умножаем на соответствующую координату другого вектора, а потом суммируем произведения: $$ (overline{a},overline{b}) = 3cdot 2 + 1 cdot 4 = 6+4=10 $$ Далее находим чему равны модули каждого из векторов: $$ |overline{a}|=sqrt{3^2+1^2} = sqrt{10} $$ $$ |overline{b}|=sqrt{2^2+4^2} = sqrt{4+16} = sqrt{20} $$ Теперь можно найти косинус угла между векторами подставив найденные значения в первую формулу: $$ cos phi = frac{(overline{a},overline{b})}{|overline{a}|cdot |overline{b}|} = frac{10}{sqrt{10}cdot sqrt{20}} = $$ $$ = frac{10}{sqrt{200}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ cos phi = frac{sqrt{2}}{2} $$ |
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Треугольники общего вида
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д15 № 27448
Найдите синус угла
В ответе укажите значение синуса, умноженное на
Решение
·
Помощь
2
Задания Д15 № 27449
Найдите косинус угла
В ответе укажите значение косинуса, умноженное на
Решение
·
Помощь
3
Задания Д15 № 27451
Найдите синус угла
В ответе укажите значение синуса, умноженное на
Решение
·
Помощь
4
Задания Д15 № 27452
Найдите косинус угла В ответе укажите значение косинуса, умноженное на
Решение
·
Помощь
5
Задания Д15 № 27454
Найдите синус угла
В ответе укажите значение синуса, умноженное на
Решение
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Содержание:
- Формула
- Примеры вычисления косинуса угла между векторами
Формула
Чтобы найти косинус угла между векторами нужно,
скалярное произведение этих векторов
разделить на произведение их длин.
В случае если векторы заданны на плоскости и имеют координаты $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, то косинус между ними вычисляется по формуле:
$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}}}$$
Если же векторы заданы в пространстве, то есть
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то косинус угла вычисляется по формуле
$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
Примеры вычисления косинуса угла между векторами
Пример
Задание. Найти косинус угла $phi$ между векторами
$bar{a}=(4 ;-3)$ и $bar{b}=(1 ;-2)$
Решение. Так как векторы заданы на плоскости, воспользуемся формулой
$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}}}$
Подставим координаты заданных векторов:
$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{4 cdot 1+(-3) cdot(-2)}{sqrt{4^{2}+(-3)^{2}} sqrt{1^{2}+(-2)^{2}}}=$$
$$=frac{4+6}{sqrt{16+9} sqrt{1+4}}=frac{10}{sqrt{25} sqrt{5}}=frac{10}{5 sqrt{5}}=frac{2 sqrt{5}}{5}$$
Ответ. $cos phi=frac{2 sqrt{5}}{5}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти косинус угла между векторами
$bar{a}=(3 ;-4 ; 0)$ и $bar{b}=(4 ;-4 ;-2)$, заданных в пространстве.
Решение. Для нахождения косинуса угла между заданными векторами, воспользуемся формулой
$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} cdot sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
Подставляя координаты векторов $bar{a}$ и $bar{b}$, получим
$$begin{aligned} cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{3 cdot 4+(-4) cdot(-4)+0 cdot(-2)}{sqrt{3^{2}+(-4)^{2}+0^{2}} sqrt{4^{2}+(-4)^{2}+(-2)^{2}}} &=\=frac{12+16+0}{sqrt{9+16+0} sqrt{16+16+4}}=frac{28}{sqrt{25} sqrt{36}}=frac{28}{5 cdot 6}=frac{14}{15} end{aligned}$$
Ответ. $begin{aligned} cos phi=frac{14}{15} end{aligned}$
Читать дальше: как найти скалярное произведение векторов.
Математика,
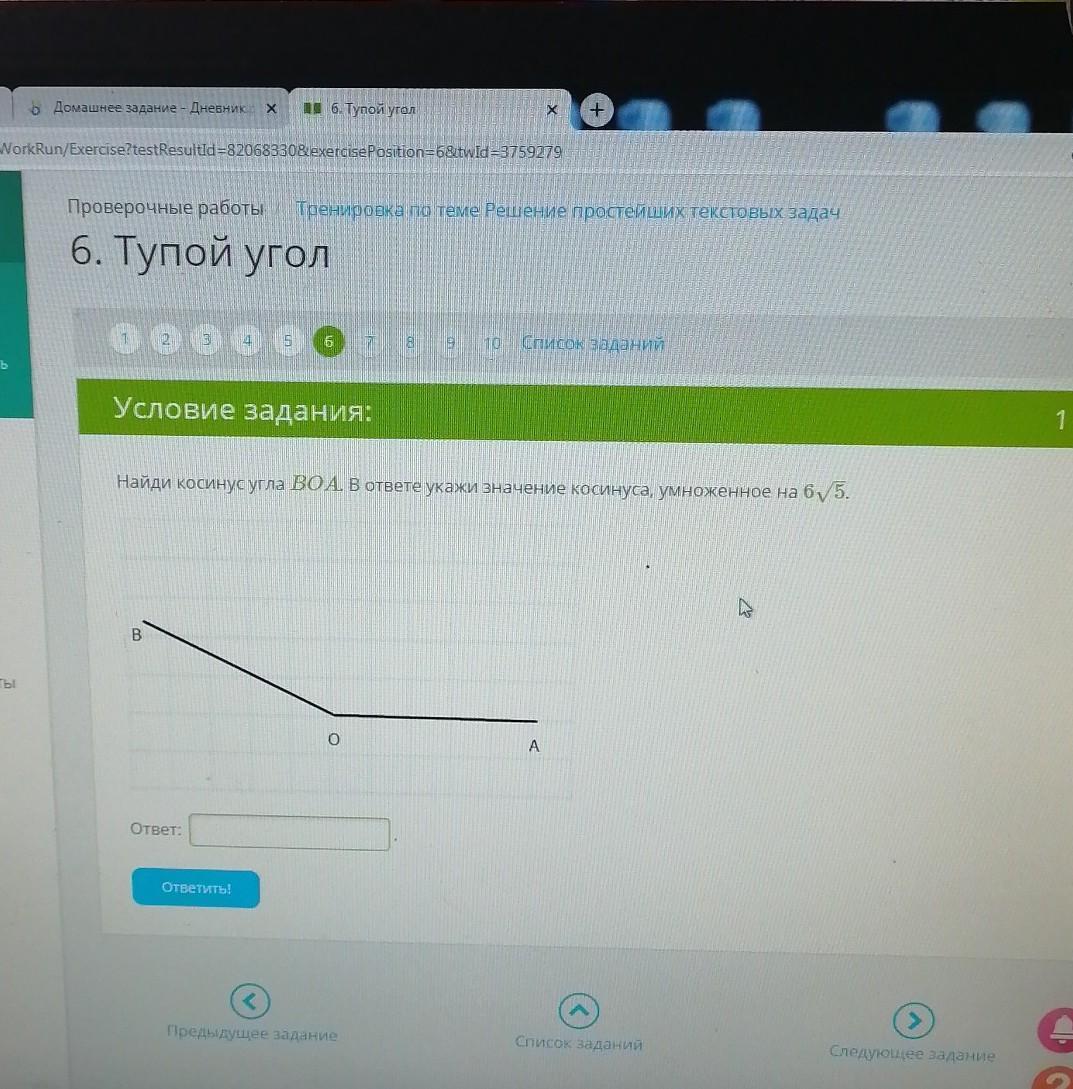
вопрос задал dark66601,
5 лет назад
найди косинус угла ВОА. В ответе укажи значение косинуса, умноженое на

Приложения:
На этот вопрос еще никто не ответил. Напишите свой ответ или воспользуйтесь поиском:
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Математика,
8 месяцев назад
ширина прямоугольника равна 17 5/14 см а длина – на 8 3/5 см больше ширины Опрели длинуи периметр прямоуголника…
Окружающий мир,
8 месяцев назад
Рабочий лист 33. Как работает выделительная система Вредные вещества Заполни схему. Под названием каждого органа напиши, какие вредные вещества он выводит из организма.Кожа,Почки,Лёгкие, Кишечник.
Музыка,
5 лет назад
представьте себя в роли композитора фильма властелина колец. какой принцип разработки образов будет положен вами в основу музыки?
Литература,
5 лет назад
1) Вспомните, когда появляется образ «темных аллей» в одноименном рассказе И. Бунина. Как о них вспоминает Надежда? А Николай Алексеевич? Кому или чему адресована эта «недобрая улыбка»?
2) В чем…
Математика,
6 лет назад
спростити вираз якщо а =2…
Алгебра,
6 лет назад
Найдите область значения функции y=(x^2+1)/x^2
Заранее спасибо…





