На шильдиках некоторых устройств можно увидеть непонятный параметр: косинус фи (cos φ). Что же этот параметр означает? В данной статье мы доходчиво и вкратце объясним что это такое.
Косинус фи (cos φ) часто называют «Коэффициент мощности». Это почти одно и то же при правильной синусоидальной форме тока.
Иногда, для обозначения коэффициента мощности используется λ, эту величину выражают в процентах, или PF.
Условные обозначения
P — активная мощность S — полная мощность Q — реактивная мощность, U — напряжение I — ток.
Что такое Косинус фи (cos φ) — «Коэффициент мощности»
Косинус фи (cos φ) – это косинус угла между фазой напряжения и фазой тока.
При активной нагрузке фаза напряжения совпадает с фазой тока, φ (между фазами) равен 0 (нулю). А, как мы знаем, cos0=1. То есть, при активной нагрузке коэффициент мощности равен 1 или 100%.
Активная нагрузка
При емкостной или индуктивной нагрузке фаза тока не совпадает с фазой напряжения. Получается «сдвиг фаз».
При индуктивной или активно-индуктивной нагрузке (с катушками: двигатели, дросселя, трансформаторы) фаза тока отстает от фазы напряжения.
При емкостной нагрузке (конденсатор) фаза тока опережает фазу напряжения.
А почему тогда косинус фи (cos φ) это тоже самое, что коэффициент мощности? Да потому что S=U*I.
Посмотрите на графики ниже. Здесь φ равно 90 косинус фи (cosφ)=0(нулю).
Емкостная нагрузка
Индуктивная нагрузка
Попытаемся вычислить мощность. Для простоты возьмем максимальное значение напряжения, равное 1 (100%) в этот момент ток равен 0(нулю). Соответственно, их произведение, то есть мощность, равны 0(нулю). И наоборот, когда ток максимальный, напряжение равно нулю.
Получается что полезная, активная мощность равна 0(нулю).
Коэффициент мощности – это соотношение полезной активной мощности к полной мощности, то есть cosφ=P/S.
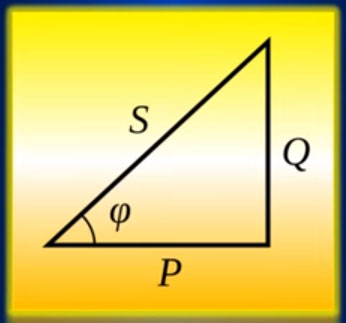
Треугольник мощностей
Посмотрите на треугольник мощностей. Вспомним тригонометрию (это что то из математики) вот здесь то она нам и пригодится.
P=U x I x cos φ
Q =U x I x sin φ
На практике.
Если подключить асинхронный двигатель в сеть без нагрузки, в холостую. Напряжение вроде как есть, ток, если замерить, тоже есть. При этом, никакой полезной работы не совершается. Соответственно, активная мощность минимальна.
Если на двигателе увеличить нагрузку, то сдвиг фаз начнет уменьшаться и, соответственно, косинус фи (cos φ) будет увеличиваться, а с ним и активная мощность.
К счастью, счётчики активной мощности фиксируют соответственно только активную мощность, что логично. И нам не приходится переплачивать за полную мощность.
Однако, у реактивной мощности есть большой минус: она создает бесполезную нагрузку на электрическую сеть из-за чего образуются потери.
Диэлектрическими потерями называют энергию, рассеиваемую в электроизоляционном материале под воздействием на него электрического поля. Способность диэлектрика рассеивать энергию в электрическом поле обычно характеризуют углом диэлектрических потерь, а также тангенсом угла диэлектрических потерь. При испытании диэлектрик рассматривается как диэлектрик конденсатора, у которого измеряется емкость и угол δ, дополняющий до 90° угол сдвига фаз между током и напряжением в емкостной цепи. Этот угол называется углом диэлектрических потерь.
Низкий коэффициент мощности и его последствия
Рассмотренное запаздывание тока относительно напряжения — это не хорошее явление. Как оно может сказаться на ваших лампочках или проводке?
- во-первых, это повышенное потребление электроэнергии
Часть энергии будет просто “болтаться” в катушке, при этом не принося никакой пользы. Правда не пугайтесь, ваш бытовой счетчик реактивную энергию не считает и платить вы за нее не будете.
Например, если вы включите в розетку инструмент или светильник с полной мощностью 100Ва, на блоке питания которого будет указано cos ϕ=0,5. То прибор учета накрутит вам только на половину от этой величины, то есть 50Вт.
- во-вторых, величина тока в проводке увеличится
- в-третьих, для эл.станций и трансформаторов это чревато перегрузкой
Казалось бы, выбросить катушку и вся проблема исчезнет. Однако, делать это нельзя.
В большинстве светильников, лампы работают не отдельно, а в паре с источниками питания. И в этих самых источниках, как раз и присутствуют разнообразные катушки.
Катушки просто необходимы как функциональная часть всей схемы и избавиться от них не получится. Например, в тех же дроссельных лампах ДРЛ, ДНАТ, люминесцентных и т.п.
Ноль означает, что полезная работа не совершается. Единица – вся энергия идет на совершение полезной работы.
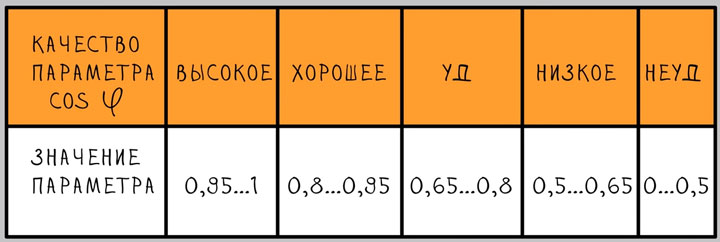
Чем выше коэффициент мощности, тем ниже потери электроэнергии. Вот таблица косинуса фи для различных потребителей:
Как измерить коэффициент мощности
Если вы не знаете точный коэффициент мощности своего прибора, или его нет на бирке, можно ли измерить косинус фи в домашних условиях, не прибегая к различным формулам и вычислениям? Конечно можно.
Для этого достаточно приобрести широко распространенный инструмент – цифровой ваттметр в розетку.
Подключая любое оборудование через него, можно легко без замеров и сложных вычислений, узнать фактический cos ϕ.
Зачастую, фактические данные могут быть даже точнее, чем написанные на шильдике, которые рассчитаны для идеальных условий.
Если он слишком низкий, что делать, чтобы привести его значение как можно ближе к единице? Можно это дело определенным образом компенсировать. Например, с помощью конденсаторов.
#электричество #электрика #коэффициент мощности #ремонт #полезные советы
Спасибо за внимание и не пропустите следующие статьи.
Подписаться.
Обратитесь к специалистам компании xiot.ru “Разумная автоматизация” и мы разработаем для Вас детальный проект любой сложности.
Приобрести оборудование Вы можете в нашем магазине xiot-shop.ru.
Больше полезных советов, обзоров, интересных статей, оборудования умных домов и новостей о нём Вы можете найти на новостной странице нашего сайта, Ютубе и Инстаграм.
Расчет коэффициента мощности, cos(φ) электродвигателя
Расчет коэффициента мощности () электродвигателя онлайн
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:

Содержание:
- Расчет мощности электродвигателя.
- Расчет тока электродвигателя.
- Расчет коэффициента мощности электродвигателя.
- Расчет КПД электродвигателя.
1. Расчет мощности электродвигателя
Расчет мощности электродвигателя по току можно произвести с помощью нашего онлайн калькулятора:
Расчет мощности трехфазного электродвигателя
Полученный результат можно округлить до ближайшего стандартного значения мощности.
Стандартные значения мощностей электродвигателей: 0,25; 0,37; 0,55; 0,75; 1,1; 1,5; 2,2; 3,0; 4,0; 5,5; 7,5; 11; 15; 18,5; 22; 30; 37; 45; 55; 75 кВт и т.д.
Расчет мощности двигателя производится по следующей формуле:
P=√3UIcosφη
где:
- U — Номинальное напряжение (напряжение на которое подключается электродвигатель);
- I — Номинальный ток электродвигателя (берется из паспортных данных электродвигателя, а при их отсутствии определяется расчетным путем);
- cosφ — Коэффициент мощности — отношение активной мощности к полной (принимается от 0,75 до 0,9 в зависимости от мощности электродвигателя);
- η — Коэффициент полезного действия — отношение электрической мощности потребляемой электродвигателем из сети к механической мощности на валу двигателя (принимается от 0,7 до 0,85 в зависимости от мощности электродвигателя);
2. Расчет тока электродвигателя
Расчет номинального и пускового тока электродвигателя по мощности можно произвести с помощью нашего онлайн калькулятора:
Расчет тока трехфазного электродвигателя
Укажите мощность электродвигателя в килоВаттах
Укажите номинальное напряжение
Укажите коэффициент мощности (cosφ)*
*при отсутствии данных укажите значение:
от 0,75 до 0,8 – для двигателей мощностью до 1,1 кВт
от 0,8 до 0,85 – для двигателей мощностью 1,1 – 7,5 кВт
от 0,85 до 0,9 – для двигателей мощностью более 7,5 кВт
*при отсутствии данных укажите значение:
от 70 до 75 – для двигателей мощностью до 1,1 кВт
от 75 до 80 – для двигателей мощностью 1,1 – 7,5 кВт
от 80 до 85 – для двигателей мощностью более 7,5 кВт
Расчет номинального тока двигателя производится по следующей формуле:
Iном=P/√3Ucosφη
где:
- P — Номинальная мощность электродвигателя (берется из паспортных данных электродвигателя либо определяется рассчетным путем);
- U — Номинальное напряжение (напряжение на которое подключается электродвигатель);
- cosφ — Коэффициент мощности — отношение активной мощности к полной (принимается от 0,75 до 0,9 в зависимости от мощности электродвигателя);
- η — Коэффициент полезного действия — отношение электрической мощности потребляемой электродвигателем из сети к механической мощности на валу двигателя (принимается от 0,7 до 0,85 в зависимости от мощности электродвигателя);
Расчет пускового тока электродвигателя производится по формуле:
Iпуск=Iном*K
где:
- К — Кратность пускового тока, данная величина берется из паспорта электродвигателя, либо из каталожных данных (в приведенном выше онлайн калькуляторе кратность пускового тока определяется приблизительно исходя из прочих указанных характеристик электродвигателя).
3. Расчет коэффициента мощности электродвигателя
Онлайн расчет коэффициента мощности (cosφ) электродвигателя
Расчет коэффициента мощности трехфазного электродвигателя
Расчет cosφ (косинуса фи) двигателя производится по следующей формуле:
cosφ=P/√3UIη
где:
- P — Номинальная мощность электродвигателя (берется из паспортных данных электродвигателя либо определяется рассчетным путем);
- U — Номинальное напряжение (напряжение на которое подключается электродвигатель);
- I — Номинальный ток электродвигателя (берется из паспортных данных электродвигателя, а при их отсутствии определяется расчетным путем);
- η — Коэффициент полезного действия — отношение электрической мощности потребляемой электродвигателем из сети к механической мощности на валу двигателя (принимается от 0,7 до 0,85 в зависимости от мощности электродвигателя);
4. Расчет КПД электродвигателя
Онлайн расчет КПД (коэффициента полезного действия) электродвигателя
Расчет КПД трехфазного электродвигателя
Укажите мощность электродвигателя в килоВаттах
Укажите номинальное напряжение
Укажите коэффициент мощности (cosφ)*
*при отсутствии данных укажите значение:
от 0,75 до 0,8 – для двигателей мощностью до 1,1 кВт
от 0,8 до 0,85 – для двигателей мощностью 1,1 – 7,5 кВт
от 0,85 до 0,9 – для двигателей мощностью более 7,5 кВт
Расчет коэффициента полезного действия электродвигателя производится по следующей формуле:
η=P/√3UIcosφ
где:
- P — Номинальная мощность электродвигателя (берется из паспортных данных электродвигателя либо определяется рассчетным путем);
- U — Номинальное напряжение (напряжение на которое подключается электродвигатель);
- I — Номинальный ток электродвигателя (берется из паспортных данных электродвигателя, а при их отсутствии определяется расчетным путем);
- cosφ — Коэффициент мощности — отношение активной мощности к полной (принимается от 0,75 до 0,9 в зависимости от мощности электродвигателя);
Оказались ли полезны для Вас данные онлайн калькуляторы? Или может быть у Вас остались вопросы? Напишите нам в комментариях!
Не нашли на сайте статьи на интересующую Вас тему касающуюся электрики? Напишите нам здесь. Мы обязательно Вам ответим.
↑ Наверх

Однако люди далекие от электротехники и позабывшие школьные уроки физики, не совсем понимают, что же означает данный параметр и зачем он вообще нужен.
Давайте рассмотрим и объясним этот косинус, как можно более простыми словами, исключая всякие непонятные научные определения, типа электромагнитная индукция. В двух словах про него конечно не расскажешь, а вот в трех можно попробовать.
Когда ток отстает от напряжения
Когда ток отстает от напряжения
Предположим перед вами есть 2 проводника. Один из этих проводников имеет потенциал. Не суть важно какой именно — отрицательный (минус) или положительный (плюс).
У другого провода вообще нет никакого потенциала. Соответственно между этими двумя проводниками будет разность потенциалов, т.к. у одного он есть, а у другого его нет.
Эту разность потенциалов как раз таки и принято называть напряжением.
Если вы соедините кончики двух проводов не непосредственно между собой, а через лампочку накаливания, то через ее вольфрамовую нить начнет протекать ток. От одного провода к другому.
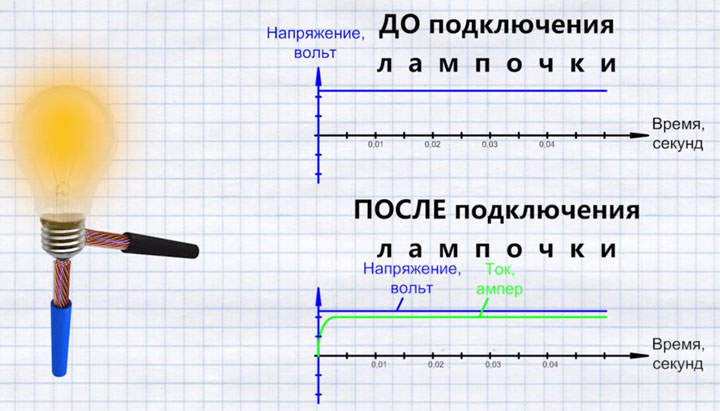
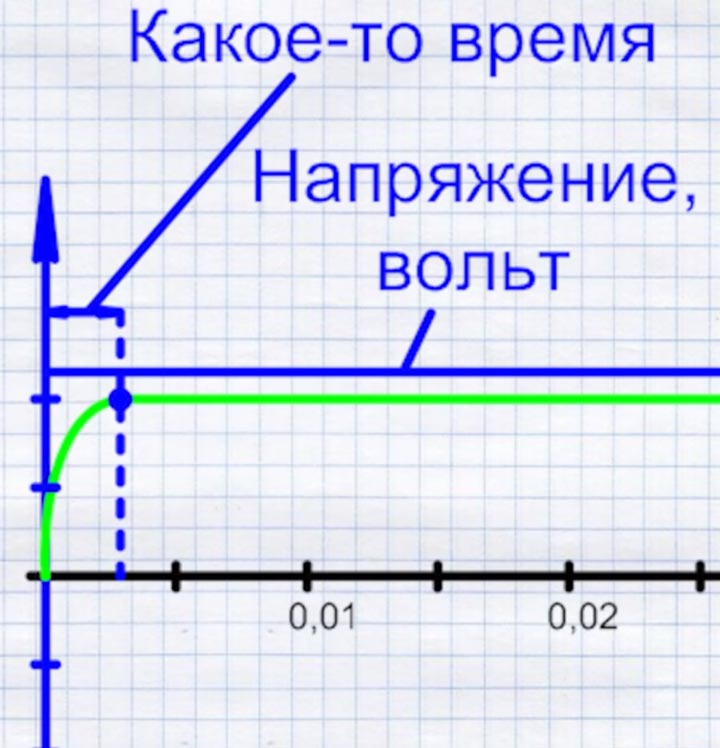
На первый взгляд может показаться, что лампочка загорается моментально. Однако это не так. Ток проходя через нить накала, будет нарастать от своего нулевого значения до номинального, какое-то определенное время.
В какой-то момент он его достигает и держится на этом уровне постоянно. То же самое будет, если подключить не одну, а две, три лампочки и т.д.
А что случится, если вместе с лампой последовательно включить катушку, намотанную из множества витков проволоки?
Изменится ли как-то процесс нарастания тока? Конечно, да.
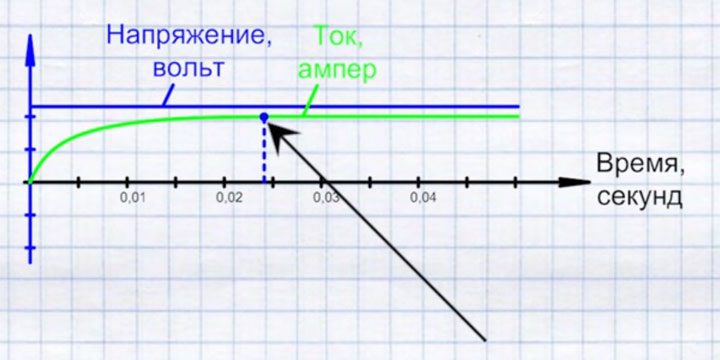
Данная катушка индуктивности, заметно затормозит время увеличения тока от нуля до максимума. Фактически получится, что максимальное напряжение (разность потенциалов) на лампе уже есть, а вот ток поспевать за ним не будет.
Его нарастание слишком медленное. Из-за чего это происходит и кто виноват? Виноваты витки катушки, которые оказывают влияние друг на друга и тормозят ток.
Если у вас напряжение постоянное, например как в аккумуляторах или в батарейках, ток относительно медленно, но все-таки успеет дорасти до своего номинального значения.
А далее, ток будет вместе с напряжением идти, что называется «нога в ногу».
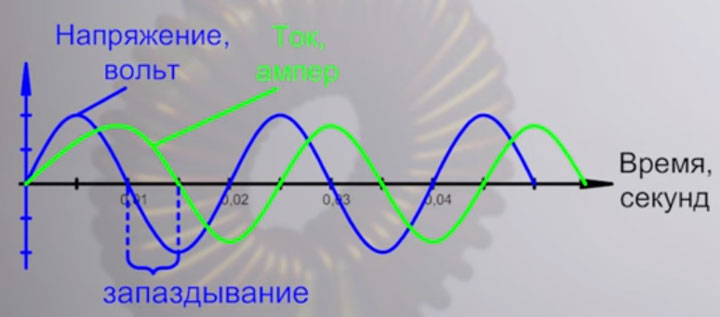
А вот если взять напряжение из розетки, с переменной синусоидой, то здесь оно не постоянно и будет меняться. Сначала U какое-то время положительная величина, а потом — отрицательная, причем одинаковое по амплитуде. На рисунке это изображается в виде волны.
Эти постоянные колебания не дают нашему току, проходящему сквозь катушку, достигнуть своего установившегося значения и догнать таки напряжение. Только он будет подбираться к этой величине, а напряжение уже начинает падать.
Поэтому в этом случае и говорят, что ток отстает от напряжения.
Причем, чем больше в катушке намотано витков, тем большим будет это самое запаздывание.
Как же это все связано с косинусом фи — cos ϕ?
Что такое коэффициент мощности
Что такое коэффициент мощности
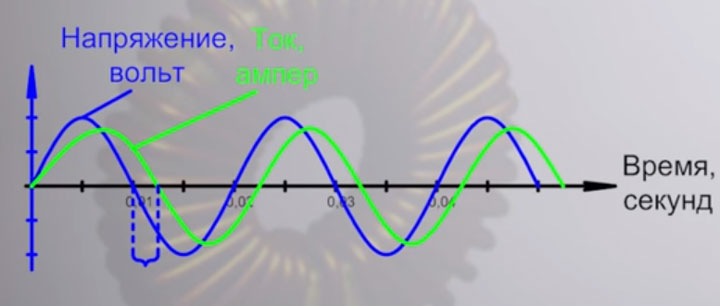
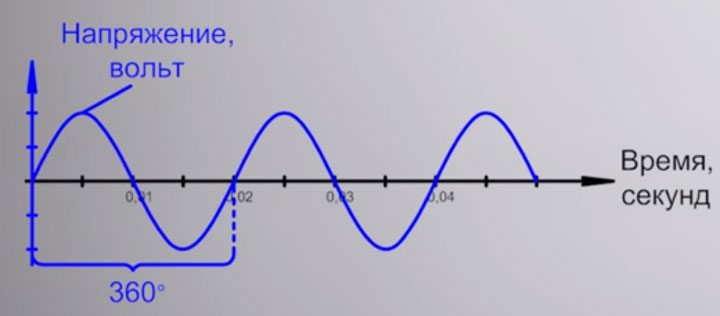
А связано это таким образом, что данное отставание тока измеряется углом поворота. Полный цикл синусоиды или волны, который она проходит от нуля до нуля, вместив в себя максимальное и минимальное значение, измеряется в градусах. И один такой цикл равен 360 градусов.
А вот угол отставания тока от напряжения, как раз таки и обозначается греческой буквой фи. Значение косинуса этого угла опаздывания и есть тот самый cos ϕ.
Таким образом, чем больше ток отстает от напряжения, тем большим будет этот угол. Соответственно косинус фи будет уменьшаться.
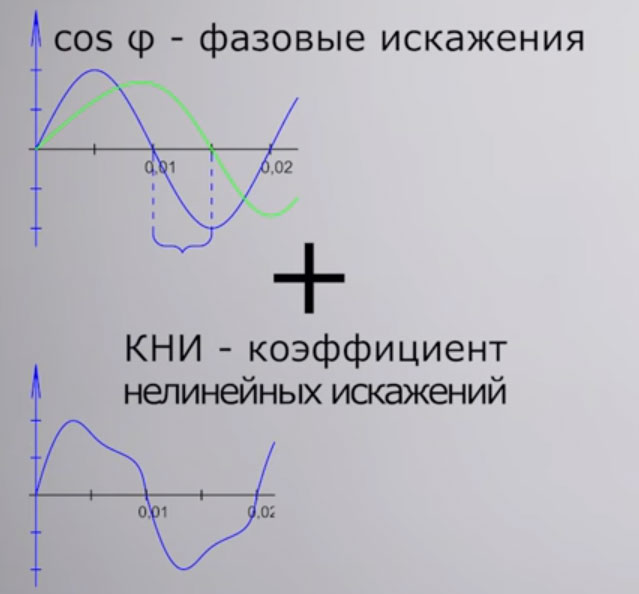
По научному, ток сдвинутый от напряжения называется фазовым сдвигом. При этом почему-то многие уверены, что синусоида всегда идеальна. Хотя это далеко не так.
В качестве примера можно взять импульсные блоки питания.
Не идеальность синусоиды выражается коэфф. нелинейных искажений — КНИ. Если сложить две эти величины — cos ϕ и КНИ, то вы получите коэффициент мощности.
Однако, чтобы все не усложнять, чаще всего под понятием коэфф. мощности имеют в виду только лишь один косинус фи.
На практике, данный коэффициент мощности рассчитывают не при помощи угла сдвига фаз, а отношением активной мощности к полной.
Активная и реактивная мощность
Активная и реактивная мощность
Существует такое понятие как треугольник мощностей. Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.
Она здорово помогает производить определенные вычисления с ними. Например, наглядно показывает отношение длин прилежащего катета (P-активная мощность) к гипотенузе (S-полная мощность).
То есть, зная угол сдвига, можно узнать, сколько активной мощности содержится в полной. Чем меньше этот угол, тем меньше реактивной составляющей находится в сети, и наоборот.
Только не путайте cos ϕ с КПД. Это разные понятия. Реактивная составляющая не расходуется, а «возвращается» на подстанцию в сеть, т.е. фактически потери ее нет. Только небольшая ее часть может тратиться на нагрев проводов.
В КПД все более четко — полезная мощность используется на нагрев — охлаждение — механическую работу, остальное уходит безвозвратно. Эта разница и показывается в КПД.
Более подробно, с графиками, рисунками и простыми словами, без особых научных формулировок обо всем этом говорится в ролике ниже.
Низкий коэффициент мощности и его последствия
Низкий коэффициент мощности и его последствия
Рассмотренное запаздывание тока относительно напряжения — это не хорошее явление. Как оно может сказаться на ваших лампочках или проводке?
- во-первых, это повышенное потребление электроэнергии

Например, если вы включите в розетку инструмент или светильник с полной мощностью 100Ва, на блоке питания которого будет указано cos ϕ=0,5. То прибор учета накрутит вам только на половину от этой величины, то есть 50Вт.
Зато по проводам питания будет проходить вся нагрузка, разогревая их бесполезной работой.
- величина тока в проводке увеличится
Вот известное наглядное видео, демонстрирующее последствия этого для проводки.
- для эл.станций и трансформаторов оно вредно перегрузкой
Казалось бы, выбрось катушку и вся проблема исчезнет. Однако делать этого нельзя.
В большинстве светильников, лампы работают не отдельно, а в паре с источниками питания. И в этих самых источниках, как раз таки присутствуют разнообразные катушки.
Катушки просто необходимы как функциональная часть всей схемы и избавиться от них не получится. Например в тех же дроссельных лампах ДРЛ, ДНАТ, люминесцентных и т.п.
Поэтому характеристика коэфф. мощности, здесь больше относится к блоку питания, нежели к самой лампе. Данный cos ϕ может принимать значение от ноля до единицы.
Ноль означает, что полезная работа не совершается. Единица – вся энергия идет на совершение полезной работы.
Чем выше коэффициент мощности, тем ниже потери электроэнергии. Вот таблица косинуса фи для различных потребителей:
Как измерить коэффициент мощности
Как измерить коэффициент мощности

Для этого достаточно приобрести широко распространенный инструмент – цифровой ваттметр в розетку.
Подключая любое оборудование через него, можно легко без замеров и сложных вычислений, узнать фактический cos ϕ.
Зачастую, фактические данные могут быть даже точнее, чем написанные на шильдике, которые рассчитаны для идеальных условий.
Если он слишком низкий, что делать, чтобы привести его значение как можно ближе к единице? Можно это дело определенным образом компенсировать. Например, с помощью конденсаторов.
Однако это тема совсем другой статьи.
Автор: Евгений Живоглядов. Дата публикации: 23 августа 2021. Категория: Статьи.
Допустим, вы купили компрессор для полива растений или электродвигатель для циркулярной пилы. В инструкции по эксплуатации помимо основных технических характеристик (таких, как потребляемый ток, рабочее напряжение, частота вращения) вы можете обнаружить такой непонятный показатель, как косинус фи (cos ϕ). Данная информация может быть указана и на пластинке (шильдике), закрепленной на корпусе прибора. В нашей статье мы постараемся объяснить простым и доступным языком всем, даже пользователям далеким от электротехнических тонкостей, как тригонометрическая функция (знакомая нам со школьной скамьи) влияет на работу всем нам привычных электробытовых приборов, и почему ее называют коэффициентом мощности.
Важно! Все нижесказанное касается только сетей переменного тока.
Активная и реактивная мощность
Существует такое понятие как треугольник мощностей. Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.
Она здорово помогает производить определенные вычисления с ними. Например, наглядно показывает отношение длин прилежащего катета (P-активная мощность) к гипотенузе (S-полная мощность).
То есть, зная угол сдвига, можно узнать, сколько активной мощности содержится в полной. Чем меньше этот угол, тем меньше реактивной составляющей находится в сети, и наоборот.
Только не путайте cos ϕ с КПД. Это разные понятия. Реактивная составляющая не расходуется, а «возвращается» на подстанцию в сеть, т.е. фактически потери ее нет. Только небольшая ее часть может тратиться на нагрев проводов.
В КПД все более четко — полезная мощность используется на нагрев — охлаждение — механическую работу, остальное уходит безвозвратно. Эта разница и показывается в КПД.
Более подробно, с графиками, рисунками и простыми словами, без особых научных формулировок обо всем этом говорится в ролике ниже.
Идеальная нагрузка
Для объяснения физического значения коэффициента мощности рассмотрим пример расчета косинуса фи для различных потребителей. Предположим, в линию переменного тока подключен идеальный конденсатор. Так как переменное напряжение непрерывно меняет свою полярность, конденсатор половину времени будет заряжаться и половину – возвращать сохраненную энергию обратно к источнику. В результате в линии будут постоянно циркулировать электроны, но чистой передачи энергии не будет. Итак, в проводнике будет и напряжение, и ток, но активной мощности не будет. Произведение U на I называется мнимой мощностью, потому что это просто математическое число, которое не имеет реального физического смысла. В этом примере коэффициент мощности равен 0.
Аналогично расчет косинуса фи для единственного идеального индуктора приведет к cos(φ) = 0, за исключением того, что его ток будет отставать от напряжения.
Теперь рассмотрим противоположный крайний случай резистивной нагрузки. В этом случае вся электрическая энергия, поступающая к ней, потребляется и преобразуется в другие виды энергии, такие как тепло. Это пример того, когда косинус фи в электрике равен 1. Все реальные схемы работают где-то в промежутке между этими двумя крайностями.
На что влияет низкий коэффициент мощности
К чему могут привести низкие показатели коэффициента мощности:
- При низком PF возрастает потребляемый нагрузкой ток. cos ϕ=P/S=P/(U•I), следовательно I=P/(U•cos ϕ). Допустим, для конкретной нагрузки необходима активная мощность P=10000 ВА при напряжении U=220 В. В идеальном варианте PF=cos ϕ=1. Тогда ток нагрузки: I=10000/(220•1)≈45 А. При PF=0,8 I=10000/(220•0,8)≈57 А. То есть при снижении PF с 1 до 0,8 ток возрастет приблизительно на 20%. Значит, это приведет к излишним затратам на электроэнергию.
- Снижение коэффициента мощности, и как следствие увеличение тока приводит к значительным энергетическим потерям в проводах, которые по закону Ома равны I•R², где R – активное сопротивление проводников. Для уменьшения этих потерь приходится увеличивать диаметр проводов, что опять же приводит к излишним экономическим затратам.
- Вышеуказанные потери расходуются на выделение тепла. В этом случае придется применять более термостойкие, а следовательно, и более дорогие изоляционные материалы).
ОБОРУДОВАНИЕ ТЕХНОЛОГИИ РАЗРАБОТКИ
Коэффициент мощности (cos φ) это параметр, характеризующий искажения формы тока, потребляемого от электросети переменного тока. Важный показатель потребителя электроэнергии. Во многом он определяет требования к питающей сети. От него зависят потери в проводах и на внутреннем сопротивлении сети.
В цепях постоянного тока мощность, впрочем, как и все остальные параметры, не меняет своего значения в течение определенного отрезка времени. Поэтому, при постоянном токе, существует единственное понятие электрической мощности как произведение значений тока и напряжения.
При переменном токе значения тока и напряжения постоянно меняются с течением времени. Мощность тоже меняется. Поэтому вводится понятие мгновенной мощности.
Мгновенная мощность.
Мгновенная мощность это произведение значения мгновенного напряжения цепи на значение мгновенного тока. На практике мощность связана с выделением тепла, механической работой и т.п. А эти явления имеют инерционный характер. Поэтому понятие мгновенной мощности не имеет практического значения, а используется для расчетов и понимания происходящих процессов.
Действующие значения тока и напряжения.
Для оценки и расчетов цепей переменного тока используются действующие значения тока и напряжения.
Действующее значение переменного тока определяется как величина такого эквивалентного постоянного тока, который проходя через то же активное сопротивление, что и переменный ток, выделяет на нем за период то же количества тепла. Математически действующее значение определяется как среднеквадратичное за период.
Вольтметры и амперметры переменного тока показывают именно действующие значения. Все операции по тепловым расчетам происходят так же, как и на постоянном токе, только с использованием действующих значений. Но это не всегда правильно.
Полная мощность.
Полная мощность вычисляется как произведение действующих значений тока и напряжения цепи.
S = U * I
В случае синусоидальной формы тока и напряжения, а также отсутствия фазового сдвига, вся полная мощность выделяется на нагрузке. Расчеты для переменного тока соответствуют анализу цепей постоянного тока, только используются действующие значения тока и напряжения.
Полная мощность фактически показывает требования к электрической сети. Измеряется она в В ·А , не в Вт.
Реактивная мощность.
Как только в цепи переменного тока появляются реактивные элементы ( индуктивность и емкость) все меняется. Реактивные элементы обладают способностью накапливать энергию и отдавать ее в цепь обратно. Появляется реактивная мощность.
Реактивная мощность не выделяется на нагрузке, не создает полезной работы. Она накапливается на реактивных элементах нагрузки ( конденсаторах, катушках индуктивности), а затем возвращается обратно в питающую сеть. Понятно, что возвращается она с потерями на проводах, на внутреннем сопротивлении питающей сети и т.п. Поэтому в любой энергосистеме стремятся уменьшить реактивную мощность до минимума.
Реактивная мощность может быть как положительной (для индуктивных цепей), так и отрицательной (для емкостной составляющей).
Единица измерения – вольт-ампер реактивный (ВАР).
Активная мощность.
На нагрузке остается активная мощность. Она и совершает полезную работу. Активная мощность это среднее значение мгновенной мощности за период.
Основные соотношения между параметрами.
Полная мощность в цепях переменного тока равна квадратному корню из суммы квадратов активной и реактивной мощностей.
S = √ ( P2 + Q2)
Активная мощность вычисляется как:
P = I * U * cos φ
I и U это действующие значения тока и напряжения.
Или:
P = S * cos φ
Т.е. активная и полная мощности связаны через коэффициент — cos φ.
cos φ – это косинус угла сдвига между напряжением питающей сети и током, потребляемым нагрузкой. Это соотношение верно только для синусоидальной формы тока и напряжения. При cos φ = 1 активная мощность на нагрузке равна полной. Вся энергия питающей сети используется для полезной работы. Происходит это только на чисто активной нагрузке, без реактивной составляющей.
cos φ и есть коэффициент мощности (КМ) для переменных цепей с током и напряжением синусоидальной формы.
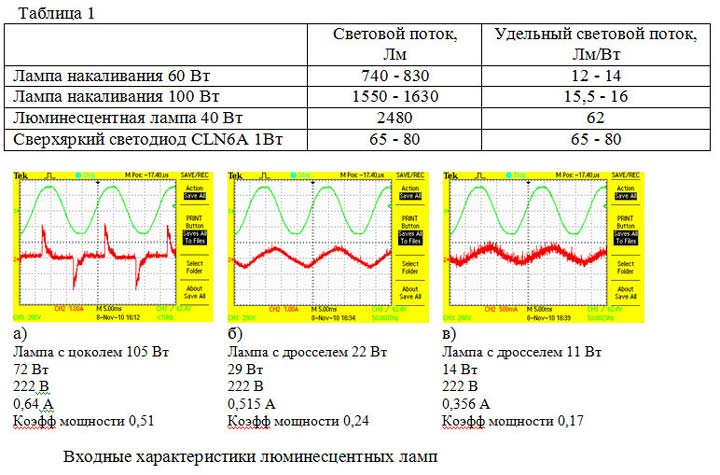
Но многие потребители энергии не только сдвигают фазу, но искажают форму тока. Примером может служить блок питания с бестрансформаторным входом. Это эквивалентная схема подключения его к питающей сети.
Для питающей сети эта схема представляет нагрузку активно-емкостного характера. Но диоды выпрямительного моста имеют нелинейную характеристику. В начале и в конце периода они закрыты и нагрузка отключена. А в середине периода диоды открываются и кроме активной нагрузки подключают к сети значительную емкость сглаживающего фильтра. В результате ток имеет искаженную форму, показанную на рисунке.
Это один из самых неприятных типов нагрузки, но и самый распространенный. Вся бытовая техника (телевизоры, компьютеры …) представляют такой характер нагрузки.
Коэффициент мощности (КМ) в переменных цепях с искаженной формой тока определяется как отношение активной мощности к полной.
λ = P / S
Следующие диаграммы иллюстрируют, как КМ влияет на работу потребителей электроэнергии.
На втором рисунке крайний, самый плохой вариант.
Сдвиг фазы между током и напряжением 90°, cos φ = 0. Видно, что диаграмма мгновенной мощности расположена симметрично относительно 0. Средняя активная мощность равна 0. Конечно, устройств с cos φ = 0 на практике не бывает, но промежуточных вариантов сколько угодно. Например, бестрансформаторный блок питания, приведенный в качестве примера выше, имеет КМ 0,6 — 0,7.
Значимость КМ можно показать простейшими расчетами.
Два потребителя электроэнергии с одинаковой активной (полезной) мощностью. У первого cos φ = 1, а у второго 0,5. Это означает, что второй потребитель потребляет от сети ток в два раза больше, чем первый. Т.к. зависимость потерь в проводах от тока имеет квадратичный характер (P = I2 * R), то потери на активном сопротивлении проводов во втором случае будут в 4 раза больше. Потребуются провода большего сечения.
Для мощных нагрузок, длинных линий электропередач высокий КМ особенно важен.
Измерение коэффициента мощности.
Для измерения cos φ используются специальные приборы – фазометры. Они применяются в сетях с потребляемым током синусоидальной формы, без искажения.
Для измерения КМ у нагрузок, искажающих ток, обычно пользуются следующей методикой.
Схема измерения коэффициента мощности.
S = U * I
Теперь надо активную мощность (показания ваттметра) разделить на полную.
λ = P / S
При отсутствии ваттметра можно использовать счетчик электроэнергии.
Для этого необходимо замерить время 10 калибровочных импульсов (миганий светодиода на корпусе счетчика). Вычислить время периода одного импульса (разделить на 10). Зная коэффициент счетчика (обычно 3200 импульсов на кВт) можно посчитать активную мощность нагрузки. С учетом того, что счетчики электроэнергии имеют класс точности 1.0, измерение получится довольно точным.
Коррекция коэффициента мощности.
Для увеличения КМ существуют специальные устройства – корректоры коэффициента мощности (ККМ). Они бываю пассивными и активными.
Для пассивной коррекции КМ в цепь питания последовательно включают дроссель. Такое решение часто применяется для трансформаторных станций катодной защиты. Но это от безвыходности. Других решений для трансформаторных станций не существует. Дроссель требуется громадных размеров, не меньше чем силовой трансформатор станции. Размеры, вес, цена станции увеличиваются практически в 2 раза, а коэффициент мощности удается поднять только до 0,85.
В инверторных станциях катодной защиты без корректора мощности (выпрямительно-емкостная нагрузка, пример был выше) КМ порядка 0,6 — 0,7. Для его увеличения используют специальные электронные модули – активные корректоры коэффициента мощности. Их схемы, построены по принципу повышающего импульсного преобразователя. Специальные управляющие микросхемы отслеживают форму тока потребления и так управляют ключом преобразователя, что она становится синусоидальной. На выходе активного ККМ формируется постоянное напряжение 380 – 400 В. Поэтому использовать их с трансформаторами невозможно.
Активные корректоры повышают КМ до 0,95 – 0,99.
Пример активного ККМ 2000 Вт для инверторной станции катодной защиты серии «ТИЭЛЛА».
Схемотехнике активных ККМ я посвящу отдельную статью.
Поддержать проект
0
Автор публикации
не в сети 1 день
Эдуард
227
Комментарии: 1779Публикации: 182Регистрация: 13-12-2015
Зависимость между тангенсом и котангенсом
[ tg alpha cdot ctg alpha=1 ]
Данное тождество справедливо только для таких углов ( alpha ), которые отличны от ( dfrac{pi}{2} z ). Иначе или котангенс или тангенс не будут определены.
Опираясь на вышеизложенные пункты, получаем, что ( tg alpha = dfrac{y}{x} ), а ( ctg alpha=dfrac{x}{y} ). Отсюда следует, что ( tg alpha cdot ctg alpha = dfrac{y}{x} cdot dfrac{x}{y}=1 ). Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.
Косинус фи
Как уже было сказано выше, значение косинуса фи в электротехнике – это величина, характеризующая степень линейности нагрузки. Для нее тоже существует формула:
cosφ = Nа / (√3*U*I).
Что касается величины «cosφ», то ее увеличение преследует несколько целей.
- Основная цель – экономия потребления электрического тока.
- Соответственно экономия цветных металлов, которые используются в обмотках электромотора.
- Максимальное использование полезной мощности агрегата.
Хотелось бы отметить вот какой момент – производственные электрические сети всегда находятся в недогруженном состоянии. Почему? Все дело в том, что не все электродвигатели постоянно работают под нагрузкой. Любой асинхронный двигатель на холостом ходе имеет косинус фи, равный приблизительно значению 0,2. При нагрузке косинус фи увеличивается до 0,85. Почему так происходит? Все опять упирается в активную и реактивную мощности. Первая при холостом ходе мотора приблизительно составляет 30%, вторая 15%. Как только нагрузка на электрический двигатель увеличивается, тут же поднимается активная составляющая, а реактивная снижается практически до нуля. Поэтому основное требование увеличения «cosφ» – это работа предприятия с полной нагрузкой.
Усредненные значения коэффициента мощности
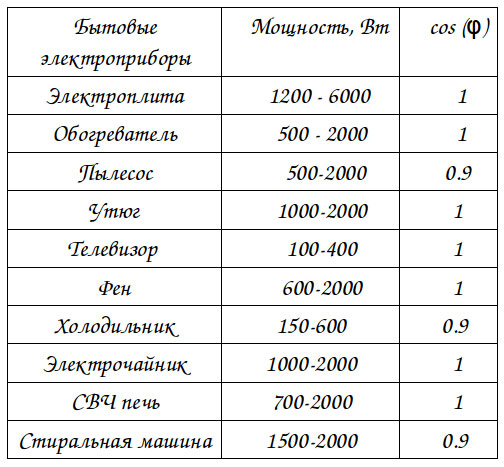
Лампы накаливания и электрические нагревательные элементы, хотя и имеют в своих конструкциях спирали, намотанные с помощью специального провода, считаются чисто активной нагрузкой для сетей переменного тока. Так как индуктивность этих элементов настолько мала, что ею, как правило, просто пренебрегают. Для таких приборов cos ϕ (или коэффициент мощности) принимают равным 1.
В разнообразных электрических ручных инструментах (дрелях, перфораторах, лобзиках и так далее) индуктивная составляющая мощности достаточно мала. Для них принято считать cos ϕ≈0,96÷0,97. Этот показатель достаточно близок к единице, поэтому его, практически, никогда не указывают в технических характеристиках.
Для мощных электродвигателей, люминесцентных ламп и сварочных трансформаторов cos ϕ≈0,5÷0,82. Этот коэффициент мощности необходимо учитывать, например, при выборе диаметра питающих проводов, чтобы они не нагрелись, и не сгорела их изоляция.