В статье мы расскажем, как находить значения:
(cos300^°), (sin(-540^°)), (cos 510^°), (sin(-135^°))
и других тригонометрических выражений без тригонометрической таблицы.
Как вычисляются синусы и косинусы углов?
Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен – абсциссе, а синус угла – ординате.
Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.
Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Получается, (cos 30^° = frac{sqrt{3}}{2}), а (sin30^° =frac{1}{2}).
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac{1}{2}=±0,5); (±frac{sqrt{2}}{2} ≈±0,707); (±frac{sqrt{3}}{2} ≈±0,866).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Для этого нужно знать несколько фактов:
- Начало отсчета находится в крайней правой точке окружности;
-
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
-
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
-
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:


- Одна точка может соответствовать разным углам;
- Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.
Пример. Отметьте угол в (90^° ) и (-90^°).
Решение:

Пример. Отметьте угол в (225^° ) и (-135^°).
Решение: (225^°=180^°+45^°)
(-135^°=-90^°-45^°)

Пример. Отметьте угол в (420^° ) и (-390^°).
Решение: (420^°=360^°+60^°)
(-390^°=-360^°-30^°)


Задание 1. Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).
Как находить синус и косинус любого угла?
Простой алгоритм:
- Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
- Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
- Найдите координаты точки, используя картинку ниже.

Пример. Вычислите (sin300^°) и (cos300^°) .
Решение: (300^°=360^°-60^°)

(cos 300^°=frac{1}{2}), (sin{300^°}=-frac{sqrt{3}}{2}).
Пример . Вычислите (sin(-540^°)) и (cos(-540^°)) .
Решение. (-540^°=-360^°-180^°).

(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos(-540^°)=-1), а (sin(-540^° )=0).
Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье.
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).

Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения (-18sqrt{2}sin(-135^°)).
Решение. (-135^°=-90^°-45^°)

Получается (-18sqrt{2} sin(-135^° )=-18sqrt{2}cdot-frac{sqrt{2}}{2}=frac{18cdotsqrt{2}cdotsqrt{2}}{2}=9cdot 2=18.)
Ответ: (18).
Пример . Найдите значение выражения (54sqrt{3}cos(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)

(54sqrt{3}cos(510^°)=54sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{54cdot sqrt{3}cdot sqrt{3}}{2}=-27cdot 3=-81.)
Ответ: (-81).
Смотрите также:
Как найти тангенс и котангенс без тригонометрической таблицы? Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.
Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.
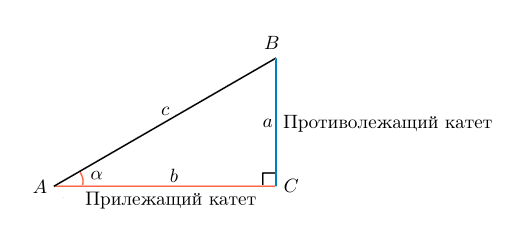
В случае с рисунком, описанным выше: cosα=bccosalpha=frac{b}{c}
Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.
Решение
Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.
a2+b2=c2a^2+b^2=c^2
62+b2=1026^2+b^2=10^2
36+b2=10036+b^2=100
b2=64b^2=64
b=8b=8
Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:
cosα=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8
Ответ
0.8
Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.
Решение
Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:
P=a+b+cP=a+b+c
25=9+4+c25=9+4+c
c=12c=12
При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:
cosα=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82
Ответ
0.820.82
Решение задач по математике от экспертов сайта Студворк!
Тест по теме “Вычисление косинуса”
В статье про прямоугольный треугольник посмотрели задачи связанные с синусами и косинусами из 1 части ОГЭ. Так что обязательно заглядывай.
Получается, что решить прямоугольный треугольник (найти все стороны и острые углы) можно довольно просто, зная всего лишь два элемента прямоугольного треугольника :две стороны (по теореме Пифагора) или сторону и острый угол (из определений синуса, косинуса, тангенса).
Но решить треугольник (найти все стороны и углы ) можно и произвольный, зная три элемента: три стороны, две стороны и угол, или два угла и сторону.
Для первых двух случаев в решении пользуются теоремой косинусов (вполне возможно эта тема вас поджидает уже на следующей неделе в школе, а может уже и была):
в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
- Если известны три стороны треугольника можно найти косинусы всех углов
- Если известны две стороны и угол между ними треугольника, то можно найти третью сторону.
В этом случае полезно пользоваться таблицей значений косинусов некоторых углов :
Рассмотрим решение задачи №16 из сборника Ященко (36 вариантов) на теорему косинусов :
Изобразим треугольник АВС и найдем в нем противолежащую сторону для угла АВС.
Из рисунка видно, что противолежащая сторона – это сторона АС.
Для стороны АС записываем теорему косинусов:
Подставим значения всех сторон:
Переносим все “свободные” числа (меняя знак) в левую часть равенства и считаем:
Находим косинус угла АВС, как неизвестный множитель:
Записываем ответ:
Если вы знаете того, кто готовится к ОГЭ, не забудьте поделиться с ним этой информацией. Всегда пригодится.
Продолжение следует…
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)
Косинус угла. Таблица косинусов.
Косинус угла через градусы, минуты и секунды
Косинус угла через десятичную запись угла
Как найти угол зная косинус этого угла
У косинуса есть обратная тригонометрическая функция – arccos(y)=x
cos(arccos(y))=y
Пример cos(60°) = 1/2; arccos(1/2) = 60°
Рассчитать арккосинус
Определение косинуса
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
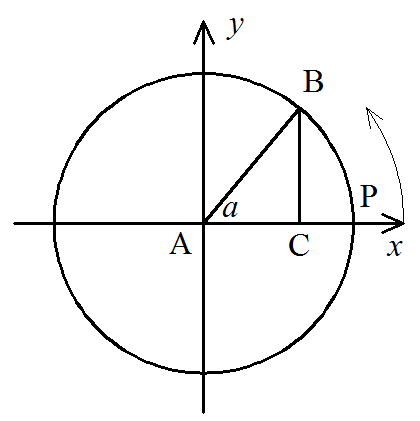
cos(α) = AC/AB
cos(-α) = cos(α)
cos(α ± 2π) = cos(α)
Таблица косинусов в радианах
cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0.7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
Таблица Брадиса косинусы
| cos(0) = 1 | cos(120) = -0.5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
| cos(9) = 0.9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0.6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0.2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
| cos(20) = 0.9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0.01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
| cos(38) = 0.7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0.9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
| cos(49) = 0.656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0.4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0.9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0.6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
| cos(77) = 0.2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0.9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0.8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
| cos(88) = 0.0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0.8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0.9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
| cos(106) = -0.2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0.6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0.9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
| cos(117) = -0.4539904997 | cos(237) = -0.544639035 | cos(357) = 0.9986295348 |
| cos(118) = -0.4694715628 | cos(238) = -0.5299192642 | cos(358) = 0.999390827 |
| cos(119) = -0.4848096202 | cos(239) = -0.5150380749 | cos(359) = 0.9998476952 |
Похожие калькуляторы
Таблица косинусов, найти значения угла косинусов
Косинус угла представляет собой одну из тригонометрических функций. Является соотношением ближнего к углу прямоугольного треугольника катета к гипотенузе. Записывается следующим образом: cos (А) = АС/АВ, где АС – ближний катет угла (А), АВ – гипотенуза.
Зачем необходимо производить такие сложные на первый взгляд вычисления? Еще с древних времен известна аксиома: знаю угол – знаю его тригонометрическую функцию. Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.
Эти данные используются не только в голых математических вычислениях. Невозможно составить даже элементарный план местности, не зная тригонометрических функций. Посредством онлайн калькулятора можно облегчить задачу и получать требуемые данные за доли секунды.
Таблица косинусов от 0° – 360°
|
|
|
|
|
|
|
|
|
|
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

