Синус, косинус, тангенс и котангенс
Острые углы в прямоугольном треугольнике.
В геометрии определения синуса, косинуса, тангенса и котангенса мы изучаем на примере острых углов в прямоугольном треугольнике.
Вот и они:

Возьмем прямоугольный треугольник АВС и распишем для него формулы для нахождения синуса, косинуса, тангенса и котангенса острых углов α и β.
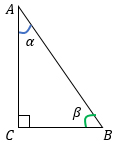
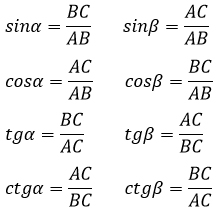
Острые углы прямоугольного треугольника обладают очень интересными сверхспособностями, которые могут пригодится при решении геометрических задач.
Во-первых, их сумма равна 90°.
Во-вторых, верны будут следующие равенства (доказать их верность очень легко – смотри предыдущие 8 формул):
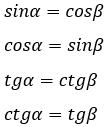
Смежные углы.
Теперь немного отстранимся от прямоугольных треугольников. Есть еще очень клевые формулы, но они подходят для смежных углов.
Пусть даны смежные углы α и β (напомню, что сумма смежных углов равна 180°).
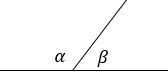
Для них будут верны следующие равенства (доказываются через формулы приведения, т.к. α = 180° – β):
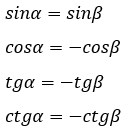
Формулы приведения.
| Функции | Углы | ||||||||
| -α | 90°-α | 90°+α | 180°-α | 180°+α | 270°-α | 270°+α | 360°-α | 360°+α | |
| sin | -sinα | +cosα | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα |
| cos | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα | +cosα | +cosα |
| tg | -tgα | +ctgα | -ctgα | -tgα | +tgα | +ctgα | -ctgα | -tgα | +tgα |
| ctg | -ctgα | +tgα | -tgα | -ctgα | +ctgα | +tgα | -tgα | -ctgα | +ctgα |
Таблица значений тригонометрических функций для “прекрасных” углов.
| α | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |
| sinα | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 |
| cosα | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
| tgα | 0 | √3/3 | 1 | √3 | – | 0 | – | 0 |
| ctgα | – | √3 | 1 | √3/3 | 0 | – | 0 | – |
Осталось это всё запомнить и научиться применять на практике)
Вообще, достаточно запомнить информацию только про синусы и косинусы, а уже через них выводить значения тангенса и котангенса.
Еще рекомендую к прочтению статью про тригонометрические тождества.
Успехов в подготовке!
С уважением, Васильева Анна.
Работа с внешними углами многоугольника с помощью тригонометрии
Определение
Смежные углы – это два угла, у которых общая вершина и сторона, а другие стороны образуют прямую.
Внешний угол многоугольника – это угол, смежный с каким-нибудь внутренним углом многоугольника.
Утверждение
Для любого действительного (alpha) верно, что
(sinleft(pi – alpharight) = sinalpha),
(cosleft(pi – alpharight) = -cosalpha).
Следствия
Синусы смежных углов равны.
Косинусы смежных углов противоположны.
Следствия
Тангенсы смежных углов либо противоположны, либо оба не существуют (когда смежные углы равны (90^circ)).
Котангенсы смежных углов либо противоположны, либо оба не существуют (когда один из смежных углов развёрнутый).
Смежные углы. Свойства смежных углов
Определение 1. Смежными называются два угла, у которых одна сторона общая, а другие стороны являются продолжениями друг друга.
На Рис.1 углы AOB и BOC смежные, так как сторона OB общая для этих углов, а стороны OA и OC являются продолжениями друг друга. Поскольку угол AOC является развернутым углом, то сумма смежных углов равна 180°:
Свойства смежных углов
1. Сумма смежных углов равна 180°
2. Если оба смежных угла равны между собой, то они являются прямыми.
3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
4. Синусы смежных углов равны.
5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.
Справедливость пунктов 2 и 3 очевидны и следуют из (1).
Доказательство пункта 4. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но (см. статью Формулы приведения тригонометрических функций онлайн)
То есть синусы смежных углов равны.
Доказательство пункта 5. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но
То есть косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.
В данной публикации мы рассмотрим, что из себя представляют смежные углы, приведем формулировку теоремы касательно них (в т.ч. следствия из нее), а также перечислим тригонометрические свойства смежных углов.
- Определение смежных углов
- Теорема о смежных углах
- Тригонометрические свойства смежных углов
Определение смежных углов
Два прилежащих угла, внешними сторонами образующие прямую, называется смежными. На рисунке ниже это углы α и β.

Если два угла имеют одну общую вершину и сторону, они являются прилежащими. При этом внутренние области этих углов не должны пересекаться.

Принцип построения смежного угла
Одну из сторон угла протягиваем через вершину дальше, в результате чего образуется новый угол, смежный с исходным.

Теорема о смежных углах
Сумма градусов смежных углов равняется 180°.
Смежн. угол 1 + Смежн. угол 2 = 180°
Пример 1
Один из смежных углов равняется 92°, чему равен второй?
Решение, согласно рассмотренной выше теореме, очевидно:
Смежн. угол 2 = 180° – Смежн. угол 1 = 180° – 92° = 88°.
Следствия из теоремы:
- Смежные углы двух равных углов равны между собой.
- Если угол является смежным с прямым (90°), значит он также равен 90°.
- Если угол является смежным с острым, значит он больше 90°, т.е. является тупым (и наоборот).
Пример 2
Допустим, у нас есть угол, смежный с 75°. Он должен быть больше 90°. Давайте проверим это.
Воспользовавшись теоремой, находим значение второго угла:
180° – 75° = 105°.
105° > 90°, следовательно угол является тупым.
Тригонометрические свойства смежных углов

- Синусы смежных уголов равны, т.е. sin α = sin β.
- Величины косинусов и тангенсов смежных углов равны, но имеют противоположные знаки (кроме неопределенных значений).
- cos α = -cos β.
- tg α = -tg β.
Смежные углы и их свойства.
Смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными и лежат на одной прямой.
Смежные углы (понятие и определение)
Свойства смежных углов
Вертикальные углы, прямой угол, развернутый угол, смежные углы, тупой угол
Смежные углы (понятие и определение):
Смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными и лежат на одной прямой. Таким образом, вместе смежные углы составляют развёрнутый угол.

Рис. 1. Смежные углы
∠ α, ∠ β – смежные углы
В свою очередь, развернутый угол – это угол, градусная мера которого равна 180°.
Поэтому сумма величин смежных углов составляет 180 градусов.
Из этого следует, что величина угла β, являющимся смежным для угла величиной α градусов, будет (180° – α) градусов.
β = 180 – α .
Свойства смежных углов:
1. Сумма величин смежных углов равна 180 градусам.
2. При пересечении двух прямых образуются две пары смежных углов.

Рис. 2. Смежные углы
∠ α, ∠ β; ∠γ, ∠δ – смежные углы,
∠ α = ∠γ; ∠ β = ∠δ
3. Угол, смежный с прямым углом, есть прямой угол. Такие углы равны между собой.

Рис. 3. Смежные углы
∠ α = ∠ β = 90°
4. В паре смежных углов один угол всегда тупой, а другой – острый либо оба угла являются прямыми.
5. Синусы смежных углов равны.
sin α = sin β
6. Косинусы и тангенсы смежных углов равны по величине, но имеют противоположные знаки.
cos α = – cos β,
tg α = – tg β
Квадрат
Овал
Остроугольный треугольник
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Смежные углы
Трапеция
Тупой угол
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
2 729
