![]()
Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):
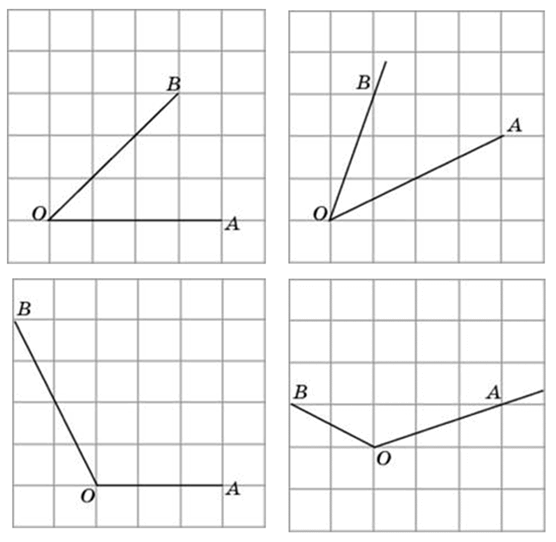
Итак, рассмотрим задание:

Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.
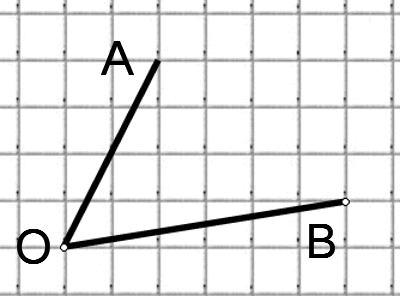
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.
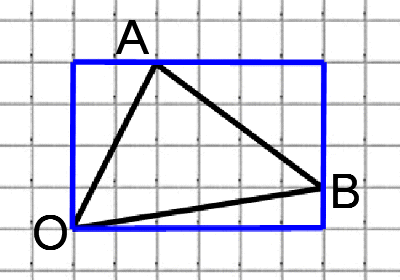
Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).
АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,
![]()
ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,
![]()
OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,
![]()
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
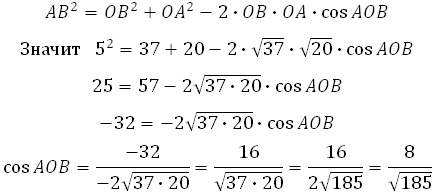
Из основного тригонометрического тождества можем найти sin AOB:
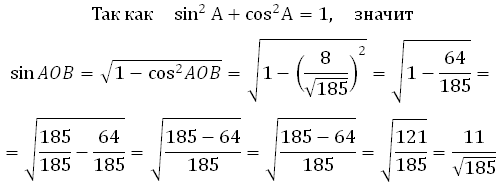
*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.
Теперь можем найти тангенс:
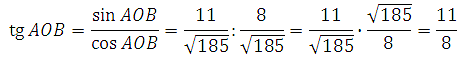
Умножим результат на 8 и запишем ответ:
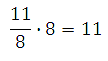
Ответ: 11
Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.
Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
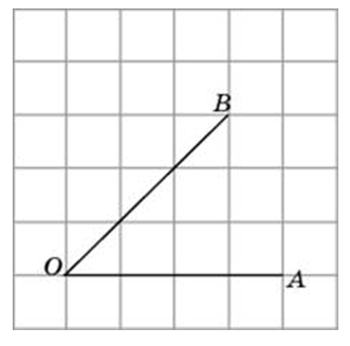
Посмотреть решение
Найдите тангенс угла AOB.
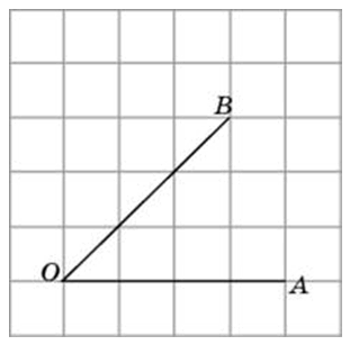
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.
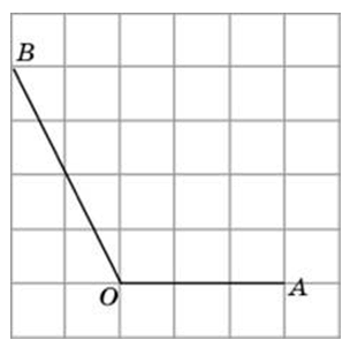
Посмотреть решение
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.
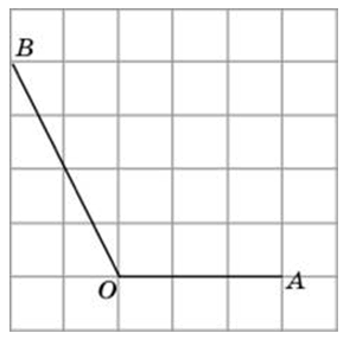
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
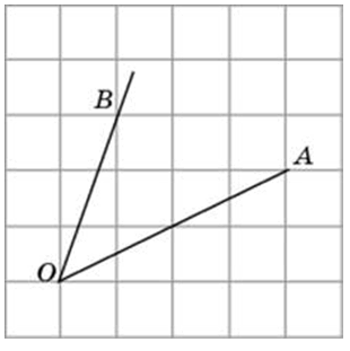
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.
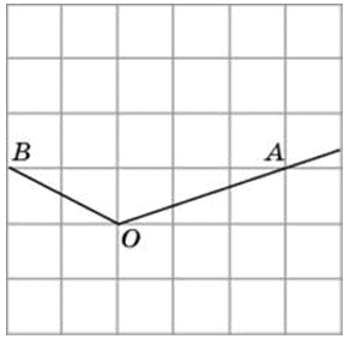
Посмотреть решение
Найдите тангенс угла AOB.
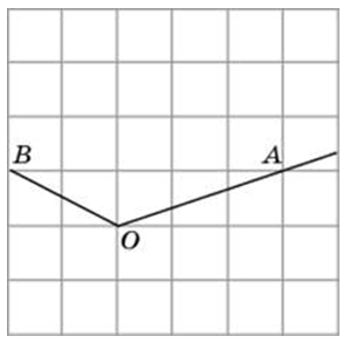
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях )
Обычно в задачах требуется найти тангенс именно острого угла, как, допустим, на этом примере:

Для этого мы строим прямоугольный треугольник, проведя линию (перпендикуляр) BD:

Далее вспоминаем определение тангенса, это отношение противолежащего катета к прилежащему.
То есть tg(BOA) = DB / DO.
Чтобы найти DO и DB достаточно будет посчитать количество клеточек.
DO = 2.
DB = 5.
Значит, tg(BOA) = 5 / 2 = 2,5.
Зная тангенс, мы можем легко найти и котангенс:
ctg(BOA) = 1 / tg(BOA) = 1 / 2,5 = 0,4.
_
А вот задача на нахождение тангенса угла по клеточкам немного другого плана (ищем тангенс угла AOB):

Если соединить точки A и B, то угол ABO будет прямым.

И тангенс можно вычислить как отношение BA к BO.
Как же нам их найти?

И BO, и BA будут гипотенузами 2 совершенно равных прямоугольных треугольников (для наглядности я их выделил красным).
Длина катетов их равна 2 и 8, а квадрат гипотенузы, как известно, равен сумме квадратов катетов.
Таким образом, у нас получится следующее:
tg(BOA) = BA / BO = √(2² + 8²) / √(2² + 8²) = 1.
И нетрудно догадаться, что треугольник этот равнобедренный с равными углами BOA и BAO по 45 градусов.
Здравствуйте, дорогие читатели. В этом выпуске поговорим о задании, которое иногда доставляет неожиданные неприятности на экзамене. Задания довольно простые, но бывают промахи. Это задания, которые сделаны как бы на тетрадном листочке в клеточку. Итак, давайте начнем.
Задание №1. УГЛЫ
Задача №1
Запомните, чтобы найти тангенс острого угла на таких картинках, обязательно нужно достроить до прямоугольного треугольника.
Вспомним, что такое тангенс острого угла прямоугольного треугольника?
Определение тангенса острого угла:
Тангенсом острого угла прямоугольного треугольника, называется отношение противолежащего катета к прилежащему. Катет BF- противолежащий угла FОВ, OF – прилежащий к углу FOB.
Задача №2
Чтобы найти тангенс угла АОВ на этой картинке, нужно достроить до прямоугольного треугольника, и найти стороны этого треугольника.
1. Достроим до треугольника ОВН и докажем, что он прямоугольный.
2. Для этого достроим на стороне ОН, ОВ и ВН прямоугольные треугольники ОСВ, ОНК и BDH. Докажем, что треугольник АВН прямоугольный.
Найдем гипотенузу ОВ прямоугольного треугольника ОСВ, гипотенузу ОН прямоугольного треугольника ОКН и гипотенузу ВН прямоугольного треугольника ВDH через теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Теперь докажем, что треугольник ОВН прямоугольный. Воспользуемся обратной теоремой Пифагора: если квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Так как равенство верно, то треугольник ОВН прямоугольный.
Теперь найдем тангенс угла АОВ
Задание №2 Расстояние
Для выполнения этого задания, проведите отрезок ВС, найдите середину его и отметим точкой К. Проведите отрезок АК, который равен 4. Ответ 4
Задание №3 Площадь
Задача №1
Задание простое, но есть ошибки по невнимательности.
Задача №2
а) Площадь треугольника и параллелограмма
Запомните! Площадь треугольника от площади параллелограмма отличается только тем, что площадь треугольника нужно делить на 2, а площадь параллелограмма нет.
б) Площадь трапеции. Чтобы найти площадь трапеции, нужно сложить основания трапеции, умножить на высоту и поделить на 2.
в) Площадь ромба равна половине произведения диагоналей.
Это не все типы заданий, что встречаются на экзамене. Продолжение следует.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Как найти тангенс угла по клеточкам
Вычисление такой величины как тангенс может потребоваться как в ходе решения тригонометрических уравнений, так и при поиске ответа задачи по геометрии. Именно во втором случае хорошим подспорьем может оказаться наличие графического изображения угла, тангенс которого необходимо найти, на разлинованной в клеточку бумаге. Как это сделать – читайте в данной статье.
1
Работа с прямоугольными треугольниками
Прежде, чем приступить к нахождению такой величины как тангенс, необходимо определиться с терминологией. Так понятие “тангенс угла” характеризует отношение противолежащего данному угла катета к прилежащему. Т. о. работа ведется в пределах прямоугольного треугольника.
Суть описанного далее алгоритма заключается в работе с прямоугольными треугольниками в рамках непосредственно определения тангенса.
Задача – определить тангенс ∠AOB.
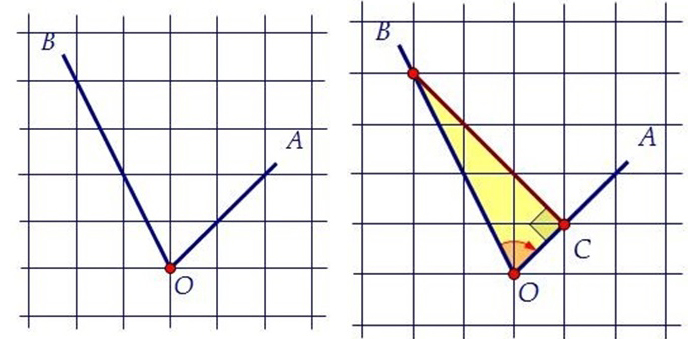
- Установите т. B на луче OB в месте его прохождения через вершину клетки.
- Из т. B опускаете перпендикуляр на луч OA. Место пересечения отмечаете как т. C.
- В результате получается прямоугольный ΔBOC, в котором находится угол ∠AOB (очевидно, что ∠BOC = ∠AOB), тангенс которого необходимо найти.
- Исходя из определения тангенса, tg∠AOB = BC / OC. Глядя на рисунок, несложно заметить что длина катета BC складывается из трех диагоналей клеток. При этом длина катета OC соответствует диагонали одной клетки. Следовательно, BC = 3OC.
- tg∠AOB = 3OC/OC = 3.
Задача – определить тангенс ∠AOB.

Расчет tg∠AOB будет основан на том, что tg(η – λ) = (tgη – tgλ) / (1 + tgη*tgλ).
- В одной из точек прохождения лучами OA и OB вершин клеток-квадратов отмечаете т. A и т. B соответственно.
- Опускаете из них перпендикуляры. В результате вы получаете 2 прямоугольных треугольника – ΔOMB и ΔOLA.
- “Расчетный” ∠AOB является разностью углов ∠AOL и ∠BOM: ∠AOB = ∠AOL – ∠BOM.
- tg∠AOB = tg(∠AOL – ∠BOM) = (tg∠AOL – tg∠BOM) / (1 + tg∠AOL*tg∠BOM). Т. о. нахождение искомой величины сводится к нахождению тангенсов углов в построенных прямоугольных треугольниках.
- tg∠AOL = AL / OL. Обратившись к рисунку заметно, что AL = 2OL. Поэтому tg∠AOL= 2OL / OL = 2.
- tg∠BOM = BM / OM. Обратившись к рисунку видно, что OM=6BM. Поэтому tg∠BOM = BM / 6BM = 1/6.
tg∠AOB = (2 – 1/6) / (1 + 2/6) = 11*3 / 6*4 = 11/8 ⇒ tg∠AOB = 1,375.
2
Использование теоремы косинусов
Задача – определить тангенс ∠AOB.
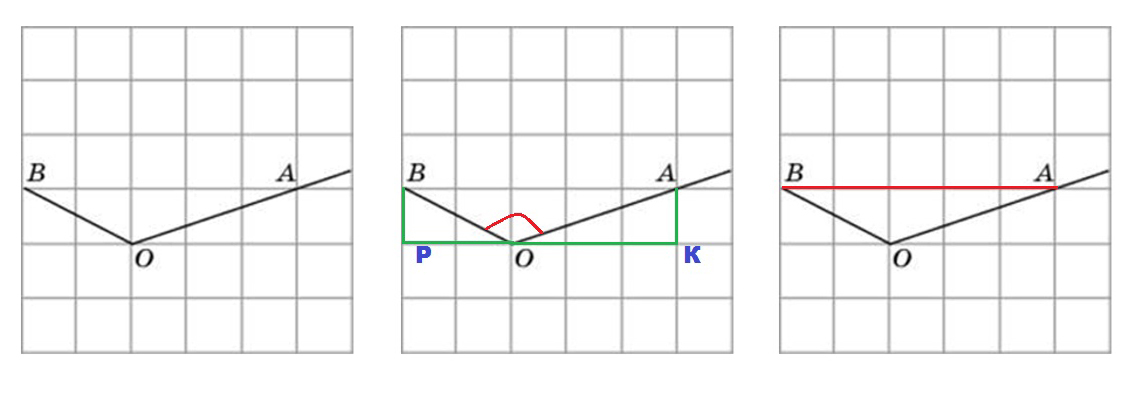
- т. A и т. B устанавливаете в точках прохождения лучей заданного угла через вершины клеток-квадратов. Опускаете из них перпендикуляры. Также отрезком соединяете между собой т. A и т. B.
- Ваша задача – вычислить длины сторон получившегося ΔAOB. Для этого обращаемся к теореме Пифагора.
- AO = √OK2 + AK2, установив длину стороны клетки как условную 1, получаем AO = √9 + 1=√10.
- OB = √BP2 + OP2, т. к. длина стороны клетки равна 1, получаем OB = √4 + 1 = √5.
- Согласно теореме косинусов, AB2 = AO2 + OB2 – 2AO*OB*cos∠AOB ⇒ cos∠AOB = (AO2 + OB2 – AB2) / 2AO*OB. Подставив числовые значения, получаем:
cos∠AOB = (10 + 5 – 25) / 2√5√10;
cos∠AOB = -10/2√5√10;
cos∠AOB = -1/√2.
- Далее воспользуемся основным тождеством тригонометрии: sinβ2 + cosβ2 = 1.
sin∠AOB = √1-1/2 = 1/√2.
- Известно, что tg∠AOB = sin∠AOB / cos∠AOB = -√2 / √2 ⇒ tg∠AOB = -1.
В зависимости от угла, тангенс которого необходимо найти, выбирайте наиболее подходящий, а главное “рабочий” алгоритм.
Тригонометрический круг со всеми значениями
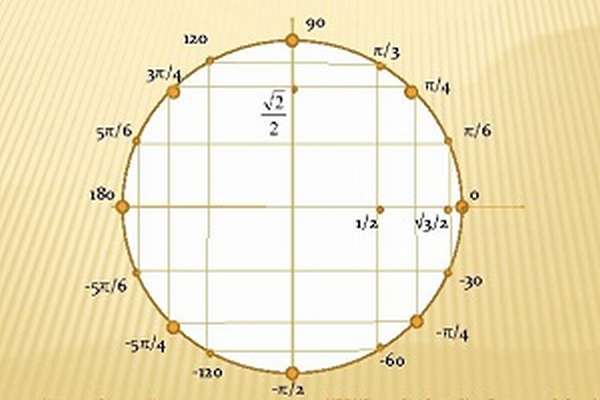
Тригонометрический круг один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.
Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.
Тригонометрическая окружность
Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.
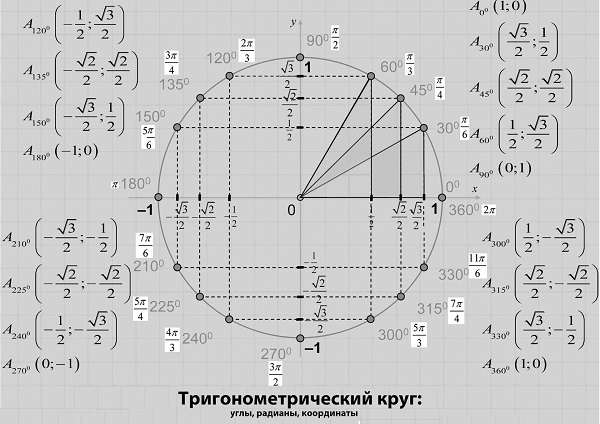
Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.
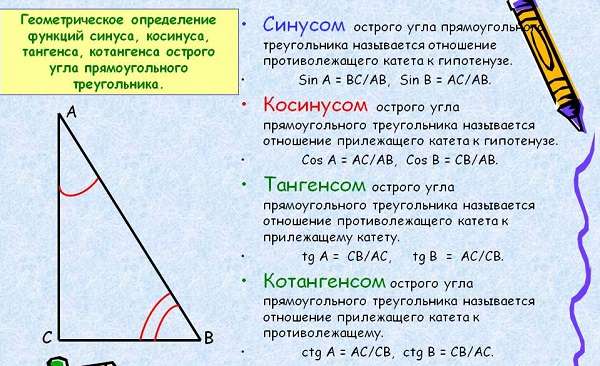
Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
Построение единичной окружности
Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.
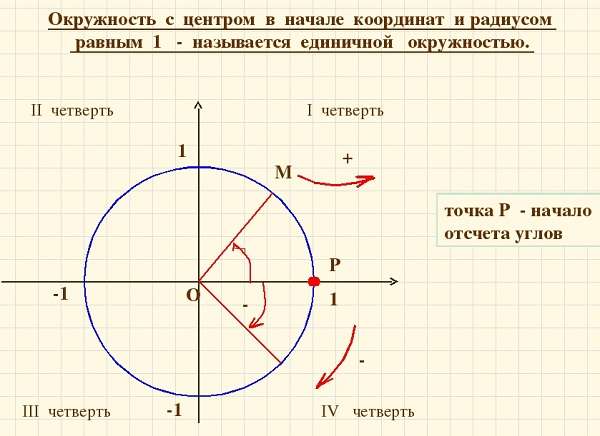
Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.
Сделать перевод этих показателей просто полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
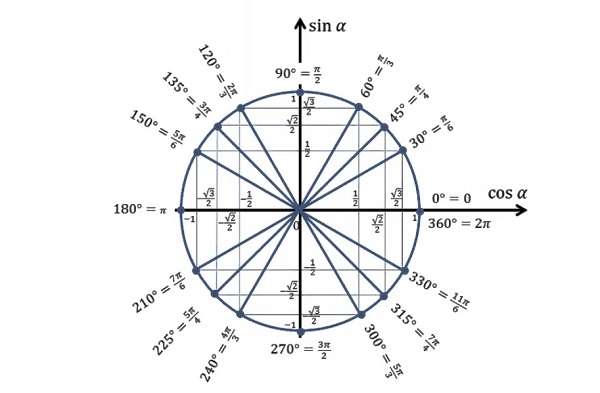
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° значения углов от 0 до ∏/2,
- от 90 до 180° значения углов от ∏/2 до ∏,
- от 180 до 270° от ∏ до 3*∏/2,
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.
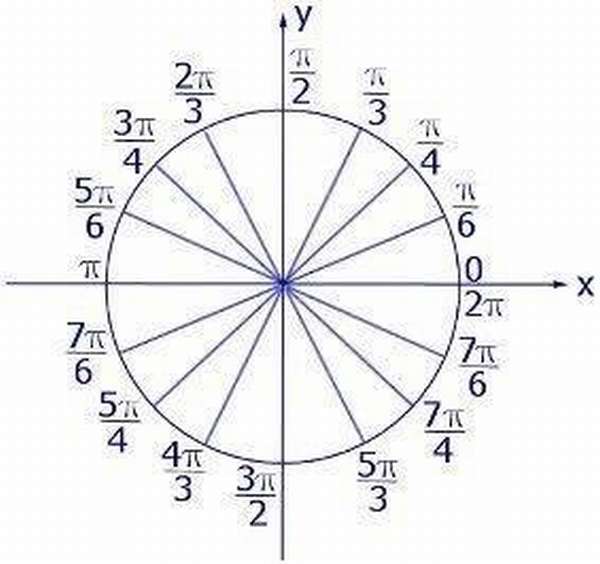
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Перевод углов из градусов в радианы
Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.
Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:
1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956
В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:
1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.

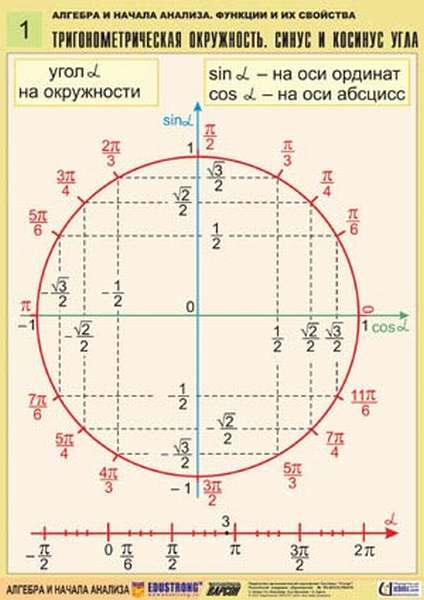
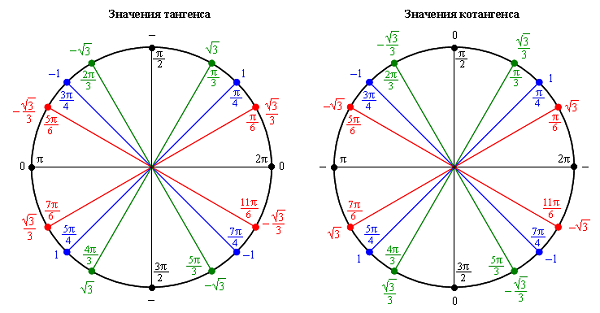
Косинус, синус, тангенс, котангенс на тригонометрической окружности
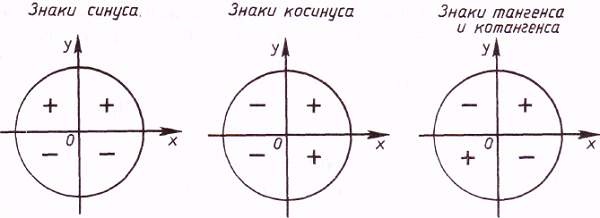
Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.
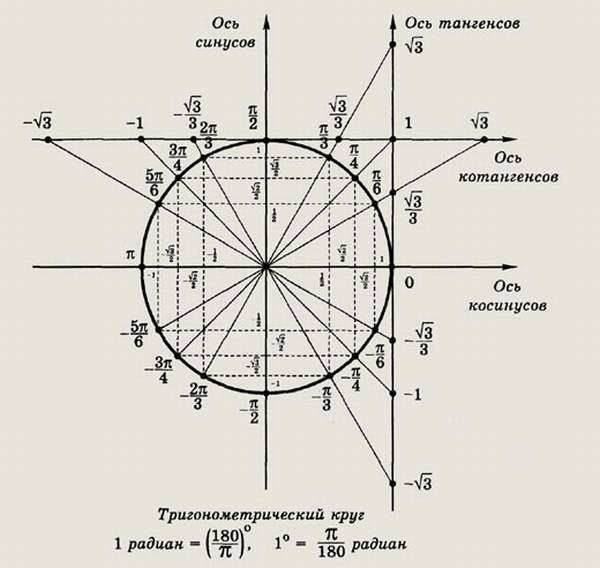
Заключение
В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.
Тригонометрический круг.
Скачать шаблоны для тригонометрии.




Здесь голубая сетка – линии декартовой системы координат. Масштаб – 1:10. В этом масштабе радиус окружности, равный единице, составляет 10 клеточек. sin30° = 1/2 составляет 5 клеточек, и т.п. Можно примерно (на глаз) отмечать или определять значения синусов и косинусов.
Зеленая радиальная сетка – лучи с шагом 15° или, что одно и то же, с шагом π/12. Удобно рисовать углы в радианах или градусах и ориентироваться в их величинах и расположении относительно четвертей круга.


Лучше всего использовать смешанную сетку – рисунок слева. Этот рисунок вы можете скачать себе на компьютер и распечатать на черно-белом принтере. Получится тонкая сетка линий, как бы нарисованных карандашом, поверх которой вам будет удобно делать свои чертежи для решения задач по тригонометрии. На втором рисунке показан пример использования такой смешанной сетки для того, чтобы проверить правильно ли определены значения sin(−π/3) и cos(−π/3). Остальные примеры и пояснения к ним расположены ниже.
Примеры.
4/π ≈ 4/3,14 ≈ 1,28
Значит 4 радиана это угол 1π + 0,28π. Кусочек 0,28π больше, чем π/4 = 0,25π, и меньше, чем π/3 ≈ 0,33π
Рисуем луч внутри сектора с границами π + π/4 и π + π/3. (Здесь серым шаблон – то, что получится после распечатки, фиолетовым – то, что отметите вы вручную.)
Отмечаем проекцию на вертикальную ось – ось синусов. Попали на отрицательный участок оси в 8-ю клеточку из 10-ти. Следовательно, sin4 ≈ −8/10 = −0,8.
Для сравнения – с помощью калькулятора получим ответ −0,7568.
Те, кто лучше ориентируется при измерении углов в градусах, могут вспомнить, что 1 радиан равен приблизительно 57,3 градуса. Соответственно, 4 рад ≈ 229º. Попробуйте самостоятельно начертить этот луч на круге.
Пример 2. Требуется убедиться, что правильно запомнились табличные значения тригонометрических функций для характерных (“геометрических”) углов.
Вспоминаем, что:
1/2 = 0,5 = 5/10 – пять клеток от центра окружности;
√2 _ /2 ≈ 1,4142/2 = 0,707 ≈ 7/10 – семь клеток от центра окружности (чуть дальше, чем граница седьмой клетки);
√3 _ /2 ≈ 1,7321/2 = 0,866 ≈ 8,7/10 – чуть дальше, чем середина девятой клетки.
Отмечаем значения синусов и косинусов на синей сетке, значения углов – на зелёной.
Совмещаем обе сетки. Если всё правильно, то в результате получатся картинки, аналогичные следующим.




Замечание.
Не забывайте – значения синусов и косинусов любых углов по абсолютной величине не превышают 1. Если вы пытаетесь записать в ответ большее число, то ищите ошибку. Возможно, вы пишите ответ в клеточках, а не в заданных единицах?
mathematichka@yandex.ru
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, © mathematichka. Копирование рисунков на других сайтах запрещено. Ставьте ссылку.
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
[spoiler title=”источники:”]
http://mathematichka.ru/school/formuly_Trig/templates.html
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
[/spoiler]

