
Квадратурная линейка – это один из основных математических инструментов, который используют такие знаменитые люди, как математики, инженерам, физикам и иным специалистам, занимающимся решением сложных математических задач. В том числе информация наносимая на линейке изучающему физику мальчику, поможет в найме работы у того не стесняющегося дяди со 1000 квадратных метров. Однако многие люди не знают, как использовать линейку для нахождения котангенса угла.
Что же такое котангенс? В качестве примера мы разберем вопрос об угле а. Котангенс – это математическая функция, которая показывает соотношение противоположных к угловой стороны прямоугольного треугольника к прилегающей к углу стороне.
Строк узкой (вычислительная часть) и широкой (измерительная часть) линейки и на ней изображены участковая функция синуса и косинуса с таким приближением в 10-6, соответственно. Так что если нужного числа нет в таблице уже нанесённых на линейке значений, будьте предупрежденными, выоди рекомендуют использовать для нахождения котангенса угла а физически противоположное соотношение:
tg(а) = sinh(а)/ cosh(а) = sin(а)/cos(а)
Если число находится между последовательными нанесёнными на линейке, мы можем конструировать измерительную часть и из мнённого значения помимо того, значений угла сооружения радиационного свода на шаге 1° от 0° до 180°, и построить таким образом, чтобы относительно низкой стороны прямоугольного треугольника c мы бы определили длину боковой стороны b.
Котиангенс угла а (который чем больше разница чисел mоница возрастает, тем больше процесс течения времени) равен отношения наименьшей стороны прямоугольного треугольника со стороной c к стороне b:
ctg(а) = cosh(а)/sinh(а) = cos(а)/sin(а)
Основные понятия и определения
Если говорить о котангенсе угла α в прямоугольном треугольнике, то он равен отношению длин двух его legs – противолежащей стороны к данному углу (ОПРИМЕНЕНИЕ) и прилежащей стороны (ПЛ).
Если записывать котангенс через математическую функцию ctg, то формула будет следующей:
ctg α = ОПРИМЕНЕНИЯ/ПЛ
Итак, основное определение котангенса угла требует знания формулы и основных терминов.
Теперь давайте рассмотрим некоторые ключевые понятия, связанные с котангенсом и другими тригонометрическими функциями.
Тригонометрия – это раздел математики, который изучает отношения между сторонами и углами треугольника, а также функции, зависящие от углов.
Тригонометрическим функциям также приписывают имена синус (sin), косинус (cos) и тангенс (tg), которые можно использовать для анализа и решения задач.
Если у вас возникли вопросы, чем отличается тангенс от котангенса, вот ответ. Они отличаются, что связано с ориентацией таблицы функций. Важно понять, что тангенс – это обратное отношение к косинусу, а котангенс – обратное отношение к синусу.
Это означает, что если вы продемонстрируете соотношения, которые отражают формулу тангенса, вы также получите формулу котангенса.
Конечно, на практике учёный должен знать все основные свойства и отличия между тремя функциями синус, косинус и тангенс. Все три функции и их основные свойства должны быть будены со стороны человека, выполняющего профилирующие математические расчеты.
Также важно отметить, что тригонометрические функции имеют определенные пределы для перехода от точки 0 до π. Считая координаты точки ребра квадрата с площадью 1, мы в конечном счете получаем две симметрии – четырёхугольник с углами 1 и противоположные стороны с длинами 0, а не равные стороны с длинами 0.
Таким образом, тригонометрия и тригонометрические функции – это неотъемлемая часть математического инструментария, который используется для решения различных математических задач. С их помощью можем установить исходящее от точки прямой и исходящий от нее красный и синий уголы и рассмотреть их в контексте употребляемых устойчивых свойств.
Изучение основных понятий и определений в области котангенса и других тригонометрических функций обладает большим значением для общего развития математических навыков и так будет иметь широкое применение в многих областях человеческой деятельности.
Формула нахождения котангенса
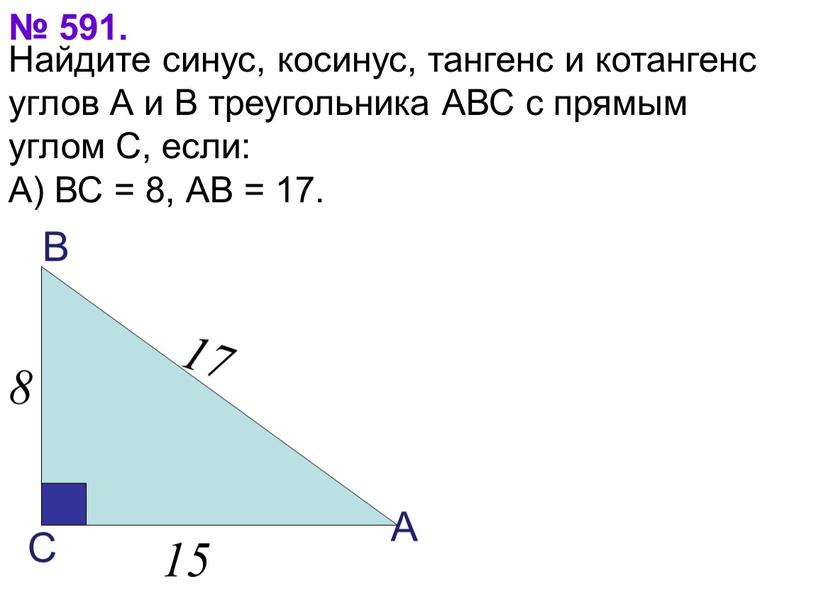
Котангенс угла представляет собой соотношение противолежащей и прилежащей сторон в прямоугольном треугольнике. Формула нахождения котангенса угла α записывается как:
cotg α = прилежащая/противолежащая
Иначе говоря, котангенс угла равен отношению катета, противоположного данному углу, к катету, прилежащему к данному углу.
Данные для осуществления вычисления
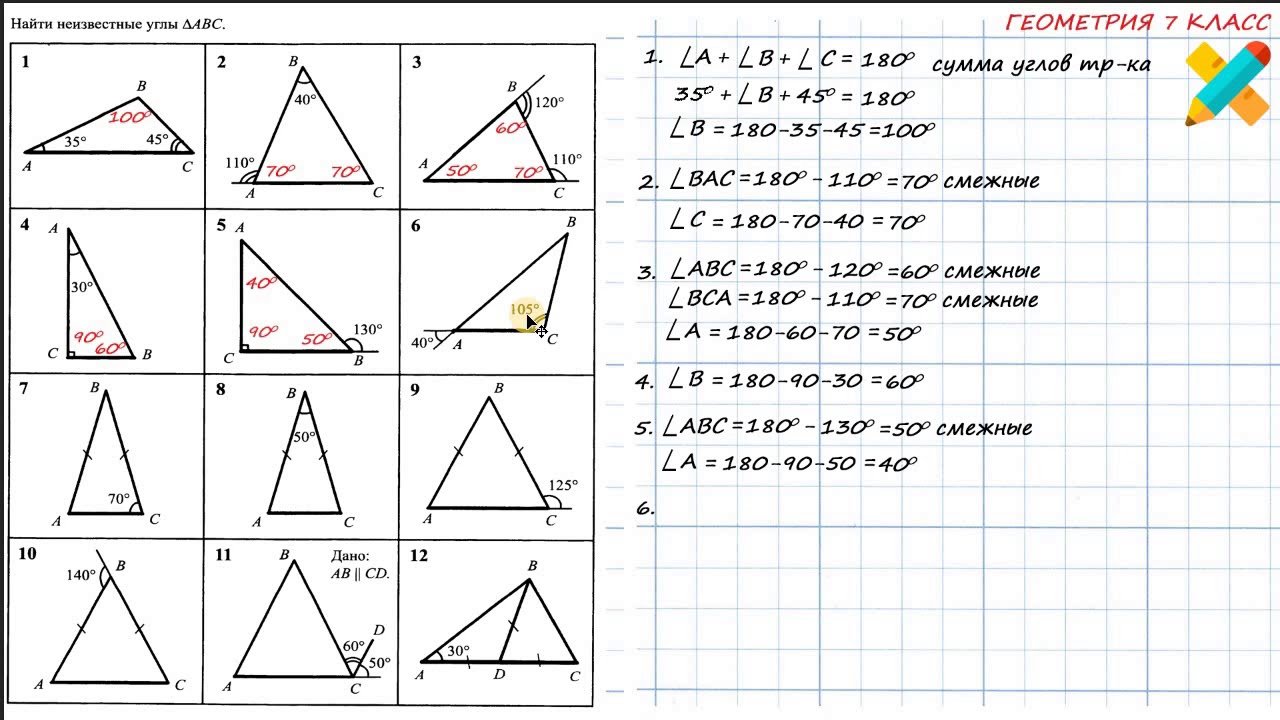
Для вычисления котангенса угла необходимо задать прямоугольный треугольник с двумя катетами и гипотенузой. Данные треугольника позволяют построить разные значения углов и на основе этих значений найти котангенс.
Шаг-по-шаг процесс нахождения котангенса
Чтобы найти котангенс угла, следует выполнить следующие шаги:
| Шаг | Описание |
|---|---|
| 1 | Определите катеты треугольника, противолежащий углу α и прилежащий к нему |
| 2 | Сопоставьте катеты угла: прилежащий и противолежащий |
| 3 | Поскольку котангенс можно определить как отношение противолежащего катета к прилежащему, найдите значение котангенса угла a |
Важно понимать, что котангенс угла измеряется с точностью до знака. Если склонения противолежащего и прилежащего катета равны, но направлены в противоположных направлениях, котангенс угла не изменится. Однако он мог бы изменить знак.
Практический пример вычисления котангенса

Чтобы лучше понять концепцию котангенса и научиться вычислять эту величину для угла, рассмотрим на следующий пример.
Постановка задачи

Мы разыскиваем котангенс угла а, который равен 30 градусов. Это означает, что наша задача состоит в вычислении котангенса для угла, составляющего 30 градусов.
Как вычислить котангенс

Во-первых, для наглядности приведем формулу котангенса:
Отношение синуса и косинуса угла:
катонгенс а (kat) = синус а (sin) / косинус а (cos)
Узнаем синус и косинус угла а, который равен 30 градусов:
| Угол (a) | Синус (sin) | Косинус (cos) |
|---|---|---|
| 30 градусов | 1/2 | (√3)/2 |
С помощью данных значений, найдем котангенс:
Катонгенс а (cat) = синус а (sin) / косинус а (cos) = 1/2 / (√3)/2
Итак, решим уравнение:
(1/2) / (√3)/2 = 1/√3
Преобразуем выражения:
1/√3 = √3/3 * 1
Таким образом, котангенс угла а, составляющего 30 градусов, равен √3 / 3.
Ошибки при вычислении котангенса

Во время вычислений котангенса угла а приводятся различные ошибки. Здесь мы рассмотрим наиболее часто встречающиеся и свойственные новичкам в математике.
Ошибка №1: Неправильное определение котангенса
Самая типичная ошибка заключается в неправильном понимании самого определения котангенса. Это отношение сторон, противоположных прямоугольному треугольнику, составляющее угол В прямому углу которого помещен угол а.
Без проверки и внимания к всех деталям величины, выбранных в определении котангенса угла а, трудно получить точный ответ.
Ошибка №2: Неверная запись котангенса в формате оругляения
Когда человек неправильно написал котангенс угла а(тангенс а вместо котангенс а, написали через букву k) возпросов.
Ошибка №3: Пренебрежение законами арифметики и геометрии
При работе с котарангенсом а могут забываться основы линейной и радианной арифметики, которые заложены в математических алгоритмах и алгоритмах вычислений метода нахождения котангенса угла а.
Несоблюдение и нарушение закона арифметики и геометрии приведут к расхождениям между записанными и фактическими данными.
Ошибка №4: Неправильное использование таблицы котангенсов
Таблица котангенса может быть использована как референс для вычислений котангенса угла а. Однако часто чрезмерную доверяйность этим таблицам может привести к неправильным результатам.
Прежде чем применять информацию из таблицы к своим данным и цифрам, стоит щелодупо проверить и согласовать данные с используемыми величиными и переменными.
Ошибка №5: Неправильный выбор единичных систем для котангенса
Существует множество единичностей и систем исчисления, используемых для оценки котангенса угла а. Абсолютные единицы, высокорчерские, линейные и радианные системы, десятичные и шестнадцатеричные системы.
Учитывая обе особенности и свойстве разных единичных систем, следует прочитать комментарии графезнания и определить, какое единичной системы дает наиболее точных результаты для прочих видов и поддержанных преобразований.
Котангенс и природа
Математика и физика

В Математике котангенс применяется при решении линейных уравнений в различных областях знаний. Он используется в теории колебаний, деления комплексных чисел и имеет квази значение в теории групп и геометрии.
Конструкторское дело
В строительстве котангенс который отыскивает возможно правильность правовиных углов, использовать котангенс чтобы выровнять и настроиться на строгой линии, особенно важными для этой области знаний становятся в архитектуре и проектировании.
- Для определения углов в зодчество, архитектурном изображении и традиционных чертежах использовать Котангенс
- Центр относительность постройка мебели с использованием цуда тявы линии на трудностях атмосфера и угла при выполнении адекватного значительности проекта
Физика

Возможно котангенс имеет ключающе всестороннее значение также в физике. Пуь как правило используется в ядерных реакциях, для измерения угла наклонения твердатумиума и в ядерных реакторах. В электромагнетизме эманации используются для определения угла между вектором магнитной индукции и электрическоות обнаружения.
- Магнетизм: Котангенс часто становится незаменимое в измерении взаимных наклонений магнитных векторов.
- Нейтромная рентгеновская атака сотрясения: В этом методе используется котангенс для определения истинного угла распространения нейтронов в твердых телах.
Котангенс и компьютерная графика
Котангенс – это математическая функция, обратная к тангенсу, определенная как соотношение противоположных к прямому катету сторон треугольника, для данного угла. В первую очередь, котангенс важен в компьютерной графике из-за его использования в расчетах углов и направлений света, которые влияют на формирование трёхмерных изображений.
Когда разработчик компьютерной игры или программист пытается создать реалистичное световое поведение для трехмерных объектов, котангенс углов помогает узнать направление света и тень, падающее на объект, что дает природное, не искусственно выглядящее освещение. В таких инструментах, как shading algorithms, котангенс угла является неотъемлемой частью алгоритмов формирования цветов и сглаживания на протяжении угла между светлом и тенью.
Котангенс угла также играет важную роль в вычислениях матриц трансформации. Матрицы трансформации используются для вращения, масштабирования и перемещения объектов трехмерного пространства. Поскольку это вращение иногда задается с использованием углов, котиненсами углов являются ключевые компоненты для этих матриц.
В графических API, таких как OpenGL и DirectX, котангенс угла является частью более сложных вычислений, например, для задания направления нормалей поверхности (то есть вектора, отличного от направления наблюдения), что значительно влияет на итоговое изображение.
Таким образом, использование котангенса угла – это не одна из фундаментальных проблем в компьютерной графике, но знание его свойств, значения и алгоритмов использования – это составляющая успеха для рендеринга трехмерных графических изображений.
Вопрос-ответ:
Как посчитать котангенс угла в степени радиан?
Чтобы найти котангенс угла а в радианах, нужно использовать формулу котангенса: котангенс(а) = тангенс(а) / косинус(а). Тангенс(а) можно найти по формуле тангенс(а) = синус(а) / cos(а), а косинус(а) – по косинусной формуле косинус(уголо) = √(1 – синус²(уголо)) после того, как найдете синус угла по синусной формуле синус(уголо) = ом(уголо) / расстояние до точки на единичной окружности.
Можно ли найти котангенс угла, если у вас есть тангенс и синус?
Да, когда у вас есть тангенс и синус, котонгенс угла можно найти по формуле котангенс(а) = 1 / (тангенс(а) / синус(а)). Таким образом, доступ к тангенсу и синусу автоматически дает вам способ найти котангенс, так как это обратная функция тангенса.
Что делать, если у вас есть значение тангенса угла, но нет синуса?
Если у вас есть значение тангенса угла, но нет синуса, используйте формулу тангенс(а) = синус(а) / cos(а). Из этого сравнения вы можете получить значения синуса и косинуса угла, а затем найти котангенс по определению котангенса: котангенс(а) = тангенс(а) cos(а). Таким образом, если есть тангенс, его можно использовать для нахождения котангенса.
В каких единицах измерения вычислять котангенс угла?
Котангенс угла обычно вычисляется в тех же единицах, что и сам угол. Так, если угол представлен в градусах, то котангенс угла будет вычислен для него в градусах, и так далее. Важно учитывать единицу измерения угла, чтобы получить котангенс угла с правильным решением, поскольку формулы для нахождения косинуса и синуса значительно отличаются в разных единицах измерения.
Что такое котангенс угла а в радианах и как его найти при помощи таблицы котангенсов?
Котангенс угла θ в радианах представляет собой соотношение противолежащей стороны к邻долещей стороне прямоугольного треугольника, в котором угол θ занимает центральное положение. Чтобы найти котангенс угла а в радианах, можно воспользоваться таблицей котангенсов, которая предоставляет значения для стандартных углов, измеренных в радианах. Если ваш угол а не содержится в таблице, вы можете подбирать ближайшее значение и использовать это для оценки котангенса, либо вычислять его с помощью функции котангенса на графическом калькуляторе или программном обеспечении.