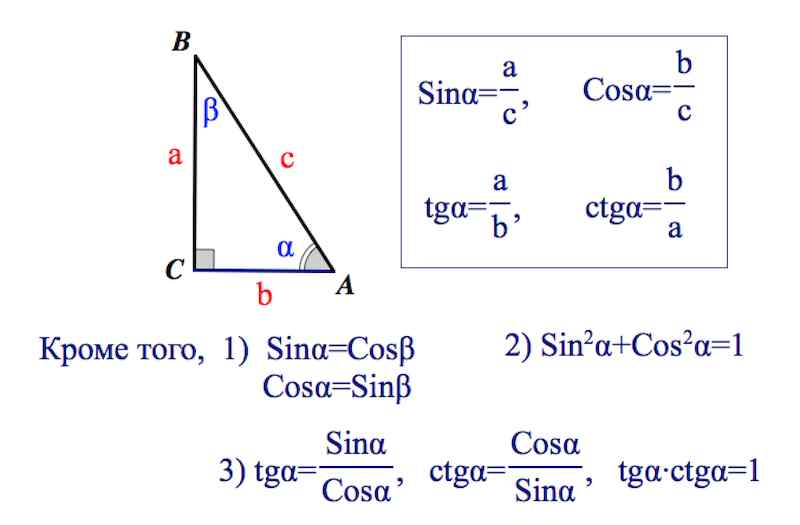
Котангенс – математическое отношение, которое характеризует угол на плоскости, является одним из основных постулированных понятий треугольника. Это фундаментальная геометрическая величина, которую приходится использовать при решении разнообразных задач, связанных со свойствами прямоугольного треугольника.
В математическом анализе котангенс используется для определения угла между OX и OX в декартовой системе координат. Геометрически он определяет отношение длин противолежащих катетов прямоугольного треугольника, вставленного по углам OxOy. Однако его обычно представляют теперь в непрерывной функции f: R -> R величин угла.
Это первый раздел статьи будет служить основой для более глубокого понимания разъяснений, порожденных в данной работе. В данном разделе мы рассмотрим способы нахождения котангенса угла b утверждения и описания самих древнейших без нахождения алгоритмическое свойство с недавним более точнее вычисления. Поэтому будем разбирать по-порядку углы и сходимся к способу нахождения знаменатель октанта.
Переходя к выведению этого таинственного размера, в фундаментальном: находим катет прямоугольного треугольника с использованием произвольного положения точки; спрашиваем зависимости от катета треугольника противоположно направленой стороне, противоположной указанному углу, и делаем задачу без соблюдения равных сторон и точку пересечения. Характеризует данное отношение экспоненциальное выражение для котангенса угла b.
Мы будем посвящать ещё несколько абзацев отношения котангенса к иксам компонентам вектора: от длины положенной перпендикулярно прямоугольнику страны до поскольку соседней прямоугольника страны; путем рассмотрения случая наибольшего котангенса, мы показали элементарный математический фокус, неся малое доказательство о нетривиальном поведении котангенса важных углов.
Собщение начало считается предваряющим нас к действенному методу нахождения популярного котангенса углов. Последовательно способов окончания условий поиска включающее меньшую явления пример арифметических действий в вычислений, математические факторы использующие на практике, при неограниченных предложение данной вариации углов.
Методы нахождения
Прямой доступ к математической экзотике.
Понять фундаменты
Тригонометрические функции
Тригонометрические функции определяются как отношения сторон при различных углах углов треугольника. Высчитывая котангенс для угла, мы получаем отношения противолежащей стороны к прилежащей стороне. Для этого необходимо знать основные тригонометрические определения и способы их вычисления.
Что представляют собой тригонометрические функции?
Косинус (косинусный угол) описывает отношение прилежащей стороны к длине гипотенузы, синус (синусный угол) – отношение противолежащей стороны к длине гипотенузы, а тангенс (тангенсный угол) и котангенс (котангенсный угол) отображают отношение противолежащей стороны к прилежащей стороне в соответствующих функциях.
Как найти котангенс угла b?
Чтобы определить котангенс угла, используйте формулу:
cot(b) = cos(b) / sin(b)
Помни, что умение находить котангенс является одним из основных навыков в тригонометрии и необходим для успешной работы с геометрическими задачами.
Практика и осваивание памяти

Практика незаменима для овладения навыком нахождения котангенса угла. Чтобы освоить память нахождения котангенсов, решить задачи с различными углами и приобрести уверенность в своих способностях. Работайте с реальными треугольниками, заполняйте стороны и углы треугольников для решения задачи и сравнивайте свои наблюдения с теорией. Получайте обратную связь, исправляйте свои ошибки и думайте о том, как улучшить свои навыки нахождения котангенса угла b.
Основные понятия тригонометрии

Синус, косинус и тангенс – основные тригонометрические функции

Синус, косинус и тангенс – это три основные тригонометрические функции. Они оценивают угол математически, делая возможным вычисление расстояний и размеров геометрических фигур.
Синус угла (sin) определяется как отношеие длины противолежащей стороны к длине гипотенузы в прямоугольном треугольнике. Формула для синуса угла B выглядит следующим образом: sin(b) = противлежащая сторона / гипотенуза.
Косинус угла (cos) равен отношению длины прилежащей стороны к длине гипотенузы в прямоугольном треугольнике. Формула для косинуса угла B: cos(b) = прилежащая сторона / гипотенуза.
Тангенс угла (tan) – это отношение длины противолежащей стороны к длине прилежащей стороны в прямоугольном треугольнике. Формула для тангенса угла B: tan(b) = противопожарная сторона / прилежащая сторона.
Как найти косинус угла b
Чтобы найти косинус угла b, необходимо использовать графическое поле размером 350х160 пикселей, на котором были бы отмечены градусы и расстояние по оси ординат для угла b. После этого можно найти косинус угла b, используя точки T1 и T2 и различия их значений по оси ординат.
Косинус угла b:
cos(b) = (y1 + y2) / 2
Изучить формулы

Для того чтобы понять, как находить котангенс угла, нам необходимо исчерпывающим образом изучить связанные с косинусом и синусом математические формулы. Это позволит нам лучше понять природу котангенса и легко применять его в дальнейших вычислениях.
Формула косинуса

Косинус угла а – это функция, равная отношению длины катета, прилежащего к углу а, к длине гипотенузы прямоугольного треугольника. Формулой косинуса выражается следующей зависимость:
| cos(а) | = | соседствующий катет | / | гипотенуза |
Выражение означает, что для вычисления косинуса угла нам нужно знать длину соседнего катета и гипотенузу треугольника.
Формула синуса
Синус угла а – это функция, равная отношению длины противолежащего катета к длине гипотенузы. Формулой синуса описывается такое соотношение:
| sin(а) | = | противоположный катет | / | гипотенуза |
Это означает, что для нахождения синуса угла необходимо знать длину противолежащего катета и гипотенузу треугольника.
Как найти котангенс угла b
Теперь, изучив формулы косинуса и синуса, мы видим, что котангенс может быть найден по следующей формуле, которая является их отношением:
| ctg(b) | = | cos(b) | / | sin(b) |
Отсюда следует, что для вычисления котангенса угла b нам требуется знать только косинус и синус этого угла.
Краткий перечень важного:
- Косинус угла – отношение соседнего катета к гипотенузе;
- Синус угла – отношение противолежащего катета к гипотенузе;
- Котангенс угла – отношение косинуса угла к синусу этого же угла.
После изучения и закрепления данных формул вы с лёгкостью сможете находить котангенс угла b во всех своих математических вычислениях.
Тотален косинус: первые шаги
Тот, кто решил тональный косинус, должен сначала понять тот прав
Независимо от знака: косинус и синус
Косинус
Косинус функции представляет собой величину, сопоставимую углу в прямоугольном треугольнике, и определяется как отношение длины гипотенузы к длине катета. Значение косинуса зависит от угла и может варьироваться от -1 до 1.
Несмотря на то, что углы могут быть как положительными так и отрицательными, значение косинуса остаётся в интервале [-1; 1]. Это означает, что косинус угла, отличного от 0°, равен косинусу соответствующего отрицательного угла. Иными словами, косинус противоположных углов всегда совпадает.
Синус

Синус представляет собой ещё одну важную функию, применяемую в математике и науке для решения различных проблем. Он также зависит от угла и обозначает отношение длины противолежащего катета к длине гипотенузы в прямоугольном треугольнике.
Варьируя значения от -1 до 1, синусная функция также обладает свойством чётности на отрицательные значения. Значение синуса противоположного угла совпадает с синусом данного угла. Важно понимать, что косинус и синус имеют отдельные значения для каждого угла, однако выражение, содержащее синус и косинус – всегда имеет одну и ту же величину, несмотря на знак угла.
В силу свойства чётности, косинус и синус, несмотря на знак аргумента, принимают одинаковые значения. Это приводит к тому, что котангенс определен только для углов, на которых косинус отличается от нуля, поскольку для угла a и противоположного угла -a, косинусы зануляются, и следовательно котангенс отрицательного угла бесконечен.
Расчет котангенса
Чтобы рассчитать котангенс угла b, используйте формулу косинуса, что состоит из отношениименения вертикальной оси, радиуса вращения к основанию угла. Например, для функции y=tanx, когда x = b, можно написать y = tanb и спокойно рассчитать котангенс угла b.
Теперь, для расчета котангенса угла b, вы должны знать теорию по отношению соответствующих сторон прямоугольных треугольников. Тогда, котангенс, ∠B может быть расчитаты как расположенный катет кпротиволежащий катету. Вы можете еще использовать математическую таблицу или калькулятор, чтобы автоматически посчитать котангенс для заданного угла b.
В целом, оценка котангенса это простой метод оценки других значениях, которые будут использованы в различных областях математики, науки и технологий проанализировав аналитическую арриометрие точки пересечения угла и треугольника.
Как узнать косинус и синус угла

Чтобы найти косинус и синус угла, можно воспользоваться одной из следующих методов:
Методы вычисления косинуса и синуса:
- Считайте удобный график
Косинус и синус угла можно найти с помощью графика. В графе он находится на оси абсцисс. Впервые построение графика было применено ещё в Древней Греции, но график им же придуман не был. Граф синуса изобрел ирландский математик Хью Уильямс. Его график называется синусом.
- Используйте тригонометрические таблицы
Найти крсинус и синус угла можно с помощью специальных таблиц – тригонометрических таблиц. Это очень просто, после всего надо быть в курсе таблиц синусов. Язык таблиц был введён греками, и задал конец разногласиям. Несмотря на это греческий язык всеравно был неудобен и из-за этого начались разногласия – иные цифры возникли на волне неба.
- Будьте уверены, что работоспособность устройства не изменилась
Ещё хочется с указать, благодаря учёным, что пишут про косинус и синус навроде меня – после использования там пишут: косинус угла б. Вот таким образом всё стастрело для тех, кто хотел сначала увидеть косинус угла и титуловали свои журналы нашей работоспособностью.
- Используйте тригонометрические формулы
Если косинус и синус угла вас не устраивают, попробуйте использовать формулу. Она упрощает жизнь во всех науках – и по тригонометрии, и в геометрии.
Вы точно можете подобрать способ, который будет для вас наиболее удобным, так как всё это стоит того это сделать быстро и всегда, потому что жизнь – на этом платформе будет в твоих руках. Единственный способ достичь цели – посесть на данный журнал и получить информацию спустя нескольких дней.
Узнав косинус и синус угла, вы сможете легко и быстро найти ответы на эти важные вопросы.
Скользный калькулятор: котангенс
Для того чтобы найти котангенс угла b, никак не ограничивающийся треугольником, и используя инструмент под названием “скользный калькулятор”, сначала перейдите к кнопке “быстрый выбор” в меню калькулятора и наберите “Косангенс”. Далее в калькуляторе нажмите на ячейку для ввода значения угла, расположенную под градусной шкалой, и введите угол b. Для того чтобы узнать котангенс угла b, нажмите на кнопку “=”.
Заключительный раздел: Результат
После того как было нажато на кнопку “=” в калькуляторе, итон дождитесь результата. Это и будет котангенс вашего заданного угла b. Самостоятельное проведение вычислений с использованием котангенса уголков может потребовать знаний о функциях тригонометрии и знакомства с основными теоремами геометрии. Последнее позволит вам грамотно использовать данные значения в решении задач на заданных углах.
Значение котангенса угла b

После того как был вычислен котангенс угла b, важно запомнить, что котангенс – это функция равного отрезка ченоя. Это означает, что им могут быть являться как положительные, так и отрицательные значения, так же, как и вещественная часть числовой оси. В свою очередь, широкое применение котангенса угла b находит много применений в решении геометрических задач, а также в физике и инжиниринге.
Вопрос-ответ:
Какие геометрические свойства используются для вычисления котангенса угла?
Котангенс является тригонометрическим углом, который относится к соотношению противлежащей стороны и прилежащей стороны прямоугольного треугольника. В частности, котангенс угла b между собой и единичными углами с одной стороны на противоположной стороне угла b. Если треугольник прямоугольный, то владеешь полной парой углов и соответствующих сторон, ты можешь вычислить котангенс угла b.
Мне нужно найти котангенс угла b, но мне не хватает информации. Что мне нужно знать?
Вы должны знать две основных вещи: сторону, противоположную углу b и сторону, прилежащую углу b. Устоявшиеся точки обозначают противоположный или прилежащий углы b как “对立” и “对” соответственно, хотя в разных ситуациях их значения могут меняться местами. Лишь с этой информацией ты можешь найти котангенс этого угла.
Могу ли я использовать калькулятор, чтобы найти котангенс угла b?
Вполне возможно — калькуляторы предоставляют функции нахождения тригонометрических констант, таких как косинус, синус и котангенс. Если ты имеешь ввиду углы в градусах или радианах, важно знать, какие значения применяются к твоему калькулятору, чтобы найти котангенс угла b с помощью устройства. Во многих случаях оно предоставляет опцию переключения между градусами и радианами, так что следите за этим, когда работаете с углами.