Как найти котангенс угла противолежащего большему катету

Что такое котангенс в прямоугольном треугольнике? Как найти котангенс? От чего зависит значение котангенса?

Определение

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

  Например, в треугольнике ABC для угла A

прилежащий катет — АC,

противолежащий катет — BC.

Поэтому котангенс угла A в прямоугольном треугольнике ABC — это

   

 Для угла B треугольника ABC

прилежащий катет — BC,

противолежащий — AC.

Поэтому, котангенс угла B в треугольнике ABC

равен отношению BC к AC:

   

Таким образом, котангенс острого угла прямоугольного треугольника — это некоторое число, получаемое в результате деления длины прилежащего к этому углу катета на длину катета противолежащего.

Так как длины катетов — положительные числа, то и котангенс острого угла прямоугольного треугольника является положительным числом.

Котангенс зависит не от длин катетов, а от их отношения. Для угла определенной величины отношение между катетами, а значит, и значение котангенса, — число постоянное.

Если изменить длины сторон треугольника, но углы оставить без изменения, то котангенсы этих углов не изменятся.

 Например,

в треугольнике ABC ∠B=30º,

в треугольнике MNK ∠M=30º.

   

   

Котангенс в прямоугольном треугольнике

Что такое котангенс в прямоугольном треугольнике? Как найти котангенс? От чего зависит значение котангенса?

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Например, в треугольнике ABC для угла A

Поэтому котангенс угла A в прямоугольном треугольнике ABC — это

Для угла B треугольника ABC

прилежащий катет — BC,

Поэтому, котангенс угла B в треугольнике ABC

равен отношению BC к AC:

Таким образом, котангенс острого угла прямоугольного треугольника — это некоторое число, получаемое в результате деления длины прилежащего к этому углу катета на длину катета противолежащего.

Так как длины катетов — положительные числа, то и котангенс острого угла прямоугольного треугольника является положительным числом.

Котангенс зависит не от длин катетов, а от их отношения. Для угла определенной величины отношение между катетами, а значит, и значение котангенса, — число постоянное.

Если изменить длины сторон треугольника, но углы оставить без изменения, то котангенсы этих углов не изменятся.

Например,

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

Давайте докажем некоторые из них.

1. Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
2. С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим.Получаем, что . Иными словами, .
3. Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
4. Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .

Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Ты нашел то, что искал? Поделись с друзьями!

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

1. В треугольнике угол равен , . Найдите .

Задача решается за четыре секунды.

2 . В треугольнике угол равен , , . Найдите .

Найдем по теореме Пифагора.

Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.

Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Калькулятор и таблица для вычисления тангенса и котангенса.

С помощью онлайн калькулятора вы сможете вычислить тангенс и котангенс с точностью от одного до шестнадцати знаков после запятой. Чтобы вычислить тангенс и котангенс, просто введите ваши данные. Так же можно воспользоватся таблицей Брадиса тангенса(tg) и котангенса(ctg) от 0° до 360°.

Калькулятор для вычисления тангенса и котангенса

Цифр после запятой

Тангенс острого угла прямоугольного треугольника.

Tg (α) острого угла прямоугольного треугольника – это отношение противолежащего катета(BC) к прилежащему катету(AC).
Пимер:
α = 40°; BC = 7,552см; AC = 9см.
tg (40°) = 7,552 9 = 0,8391

Котангенс острого угла прямоугольного треугольника.

Ctg (α) острого угла прямоугольного треугольника – это отношение прилежащего катета(AC) к противолежащему катету(BC).
Пимер:
α = 40°; AC = 9см; BC = 7,552см.
ctg (40°) = 9 7,552 = 1,1918

[spoiler title=”источники:”]

http://ege-study.ru/ru/ege/materialy/matematika/sinus/

http://max-calc.ru/Trigonometriya/Tg-Ctg.html

[/spoiler]

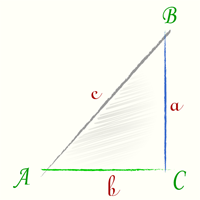
Котангенс угла ctg(A) — есть отношение прилежащего катета b к противолежащему катету a [ ctg(A) = frac{b}{a} ]

Котангенс угла — ctg(A), таблица

0° Котангенс угла 0 градусов	$ ctg(0°) = ctg(0) = infin $	∞
30° Котангенс угла 30 градусов	$ ctg(30°) = ctgBig(Largefrac{pi}{6}normalsizeBig) = sqrt{3} $	1.732
45° Котангенс угла 45 градусов	$ ctg(45°) = ctgBig(Largefrac{pi}{4}normalsizeBig) = 1 $	1.000
60° Котангенс угла 60 градусов	$ ctg(60°) = ctgBig(Largefrac{pi}{3}normalsizeBig) = Largefrac{1}{sqrt{3}}normalsize $	0.577
90° Котангенс угла 90 градусов	$ ctg(90°) = ctgBig(Largefrac{pi}{2}normalsizeBig) = 0 $	0

Вычислить, найти котангенс угла ctg(A) и угол, в прямоугольном треугольнике

Вычислить, найти котангенс угла ctg(A) по углу A в градусах

Вычислить, найти котангенс угла ctg(A) по углу A в радианах

Котангенс угла — ctg(A)	стр. 225

В прямоугольном треугольнике всегда заданы три стороны, из которых две, именуемые катетами, образуют прямой угол в 90°, а третья сторона – гипотенуза, их соединяет. Все тригонометрические отношения в таком треугольнике строятся на делении одной стороны на другую, и так как катетов два, то используемый в формуле катет может быть либо противолежащим – находящимся напротив угла α, и не имеющий с ним общих точек, либо прилежащим – являющимся непосредственно стороной угла α, и выходящим из него. Так как отношением противолежащего катета к прилежащему является тангенс, то другим отношением катетов будет котангенс, где в числителе дроби находится прилежащий катет (как и в косинусе), а в знаменателе противолежащий
.

В отличие от тандема синус-косинус, которые оба отталкиваются от гипотенузы в знаменателе, тангенс и котангенс используют в формулах исключительно катеты в разном порядке. Таким образом, мы получаем не только два разных отношения, соответствующих всем законам тригонометрии, но и два отношения, являющихся обратными друг и другу и взаимно конвертируемыми
.

Таблица котангенсов

Котангенс угла 0° градусов	∞	∞
Котангенс угла 30° градусов	√3	1.732
Котангенс угла 45° градусов	1	1.000
Котангенс угла 60° градусов	1/√3	0.577
Котангенс угла 90° градусов	0	0.000

Примеры:

(ctg⁡:30^° =sqrt{3})
(ctg⁡:(frac{π}{3})=frac{1}{sqrt{3}})
(ctg:⁡2=-0,487…)

Содержание:

• Аргумент и значение
• 
  Котангенс острого угла
• 
  Котангенс числа или любого угла
• 
  Знаки по четвертям
• 
  Связь с другими функциями

Аргумент и значение

Аргументом может быть:
– как число или выражение с Пи: (1,3), (frac{π}{4}), (π), (-frac{π}{3}) и т.п.
– так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.

Для обоих случаев значение котангенса вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).

Значение котангенса – всегда действительное число (возможно, иррациональное): (1), (sqrt{3}), (-frac{1}{sqrt{3}}), (-0,1543…)

Котангенс острого угла

Пример:

1) Пусть дан угол и нужно определить (ctgA).

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить (ctg;A).

Вычисление котангенса числа или любого угла

Пример. Вычислите (ctg: frac{5π}{6}).
Решение: Найдем сначала (frac{5π}{6}) на круге. Затем найдем (cos:⁡frac{5π}{6}) и (sin:frac{5π}{6}), а потом поделим одно на другое.

(ctg:frac{5π}{6}=)(frac{cos⁡:frac{5π}{6}}{sin⁡:frac{5π}{6}})(=-frac{sqrt{3}}{2}:frac{1}{2}=-frac{sqrt{3}}{2} cdot frac{2}{1}=-sqrt{3})

Ответ: (-sqrt{3}).

Пример. Вычислите (ctg:frac{π}{2}).

Решение: Чтобы найти котангенс пи на (2) нужно найти сначала косинус и синус (frac{π}{2}). И то, и другое найдем с помощью тригонометрического круга:

Точка (frac{π}{2}) на числовой окружности совпадает с (1) на оси синусов, значит (sin:frac{π}{2}=1). Если из точки (frac{π}{2}) на числовой окружности провести перпендикуляр к оси косинусов, то мы попадем в точку (0), значит (cos:⁡frac{π}{2}=0). Получается: (ctg:frac{π}{2}=)(frac{cos:⁡frac{π}{2}}{sin:⁡frac{π}{2}})(=)(frac{0}{1})(=0).

Ответ: (0).

Пример. Вычислите (ctg:(-765^circ)).
Решение:   (ctg: (-765^circ)=)(frac{cos:(-⁡765^circ)}{sin:⁡(-765^circ)})
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).

(sin⁡(-765^°)=-frac{sqrt{2}}{2});
(cos⁡(-765^°)=frac{sqrt{2}}{2}) ;
получается (ctg(-765^°)= frac{sqrt{2}}{2} ∶ -frac{sqrt{2}}{2}=-1).

Ответ: (-1).

Пример. Найдите (ctg:frac{π}{3}).
Решение:   (ctg: frac{π}{3}=)(frac{cos:⁡frac{π}{3}}{sin:⁡frac{π}{3}}). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
(sin⁡(frac{π}{3})=frac{sqrt{3}}{2});
(cos⁡(frac{π}{3})=frac{1}{2}) ;
получается (ctg(frac{π}{3})=frac{1}{2} ∶ frac{sqrt{3}}{2}= frac{1}{2} cdot frac{2}{sqrt{3}}=frac{1}{sqrt{3}}).

Ответ: (frac{1}{sqrt{3}}).

Однако можно определять значение котангенса и напрямую через тригонометрический круг – для этого надо на нем построить дополнительную ось:

Ось котангенсов – это фактически копия оси косинусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси косинусов.

Пример. Вычислите (ctg:frac{π}{4}).
Решение:   
1) Отмечаем (frac{π}{4}) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется (1).

Ответ: (1).

Пример. Найдите значение (ctg: 30°) и (ctg: (-60°)).
Решение:   
Для угла (30°) ((∠COA)) котангенс будет равен (sqrt{3}) (приблизительно (1,73)), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось котангесов.
(ctg;(-60°)=frac{sqrt{3}}{{3}}) (примерно (-0,58)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.

При этом котангенс не определен для:
1) всех точек (C) (значение в Пи: …(0), (2π), (4π), (-2π), (-4π) …; и значение в градусах: …(0°),(360°), (720°),(-360°),(-720°)…)
2) всех точек (D) (значение в Пи: …(π), (3π), (5π), (-π), (-3π), (-5π) …; и значение в градусах: …(180°),(540°),(900°),(-180°),(-540°),(-900°)…) .

Так происходит потому, что в этих точках синус равен нулю. А значит, вычисляя значение котангенса мы придем к делению на ноль, что запрещено. И прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось котангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках котангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений он может быть найден).

Из-за этого при решении тригонометрических уравнений и неравенств с котангенсом необходимо учитывать ограничения на ОДЗ.

Знаки по четвертям

С помощью оси котангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак котангенса для нее описанным выше способом. У всей четверти знак будет такой же.

Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение котангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

Связь с другими тригонометрическими функциями:

– синусом того же угла: формулой (1+ctg^2⁡x=)(frac{1}{sin^2⁡x}) 

– косинусом и синусом того же угла: (ctg⁡:x=)(frac{cos:⁡x}{sin⁡:x}) 

– тангенсом того же угла: формулой (tg⁡:x=)(frac{1}{ctg:x}) 
Другие наиболее часто применяемые формулы смотри здесь.

Смотрите также:
Формулы приведения
Решение уравнений (tgx=a) и (ctgx=a)