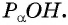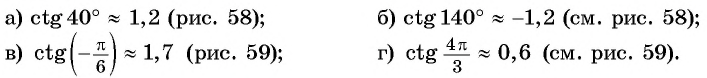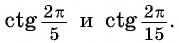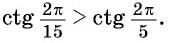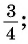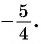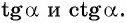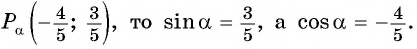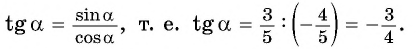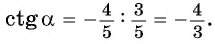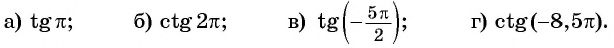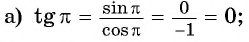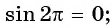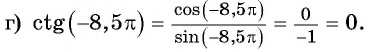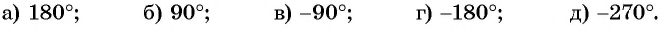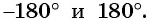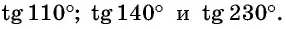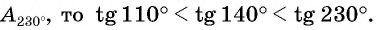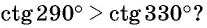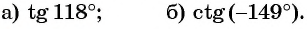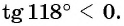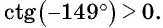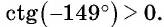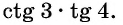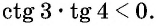Видеоурок: Синус, косинус, тангенс и котангенс угла
Лекция: Синус, косинус, тангенс, котангенс произвольного угла

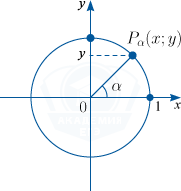
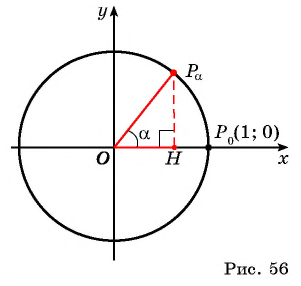
Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР, который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ. Так как окружность имеет радиус, равный единице, то ОР = R = 1.
Если с точки Р опустить перпендикуляр на ось ОХ, то получим прямоугольный треугольник с гипотенузой, равной единице.
Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным, если же он двигается против движения часовой стрелки – положительным.

Синусом угла данной окружности, образованного радиусом-вектором ОР, является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, получим, что
А так как R = 1, то sin(α) = y0.
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой – отрицательное.
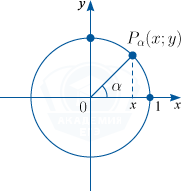
Косинусом угла данной окружности, образованного радиусом-вектором ОР, является абсцисса точки Р вектора на окружности.
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Косинус произвольного угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе, получим, что
А так как R = 1, то cos(α) = x0.
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей – отрицательное.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
Котангенсом произвольного угла называется отношение косинуса к синусу.
Рассматривая прямоугольный треугольник – отношение прилежащего катета к противолежащему, то есть абсциссы к ординате.
Так как ордината находится в знаменателе дроби, то котангенс не может существовать при угле альфа, равном нулю градусов.
Котангенс принимает те же значения в четвертях единичной окружности, что и тангенс.
Все перечисленные функции являются периодичными. Косинус и синус имеют период 360 градусов, то есть 2Пи, а тангенс и котангенс 180 градусов, то есть Пи.
Содержание:
- Котангенс угла в треугольнике
- Котангенс произвольного угла
Котангенс угла в треугольнике
Определение
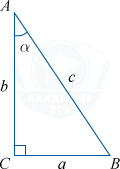
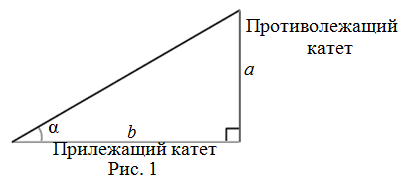
Котангенс острого угла прямоугольного треугольника – это отношение прилежащего к этому углу катета
к противолежащему катету (рис. 1):
$$operatorname{ctg} alpha=frac{b}{a}$$
Замечание
Как можно отметить, котангенс и тангенс угла связаны между собой:
$$operatorname{ctg} alpha=frac{1}{operatorname{tg} alpha}$$
Пример
Задание. Найти котангенс острого угла прямоугольного треугольника, если известно, что прилежащий
к этому углу катет равен 4 см, а противолежащий в два раза больше.
Решение. Согласно условию противолежащий катет равен:
$a = 4 cdot 2 = 8$ (см)
Тогда котангенс угла
$$operatorname{ctg} alpha=frac{4}{8}=frac{1}{2}$$
Ответ. ctg $alpha=frac{1}{2}$
Котангенс произвольного угла
Определение
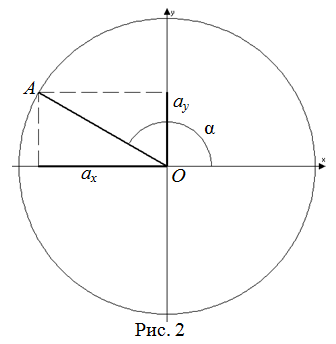
Котангенсом произвольного угла
$alpha$, образованного осью
$O_x$ и произвольным радиус-вектором
$overline{O A}=left(a_{x} ; a_{y}right)$ (рис. 2), называется отношение
проекции этого вектора на ось
$O_x$ к его проекции на ось $O_y$:
$$operatorname{ctg} alpha=frac{a_{x}}{a_{y}}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Чему равен котангенс угла, образованного вектором $bar{a} = (-3;-4)$ и осью абсцисс.
Решение. Проекция на ось абсцисс равна
$a_x=-3$, на ось ординат –
$a_y=-4$, а тогда
$$operatorname{ctg} alpha=frac{-3}{-4}=frac{3}{4}$$
Ответ. $operatorname{ctg} alpha=frac{3}{4}$
Читать дальше: что такое биссектриса угла.
Содержание:
Построим точку
По определению тангенса острого угла получим:
Определение тангенса угла
Определение:
Тангенсом угла 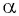
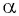
Например,
Используя определение тангенса угла и значения синуса и косинуса этого угла, найдем также значения тангенсов углов
Поскольку 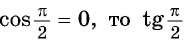
Через точку 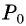
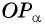
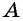
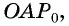
Из подобия треугольников 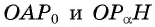
Поскольку 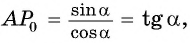
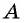
Прямая, перпендикулярная оси абсцисс, проходящая через точку 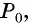
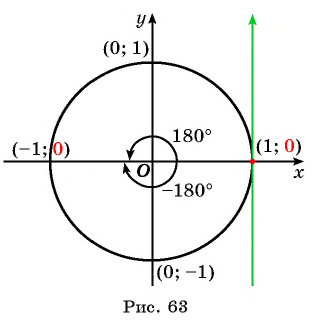
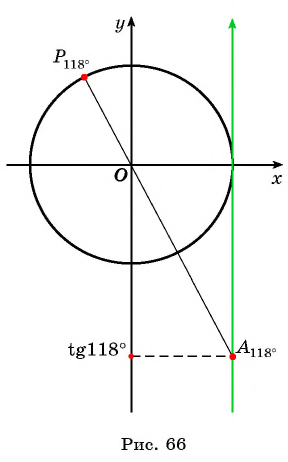
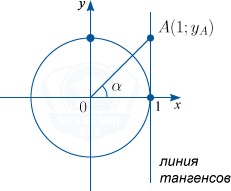
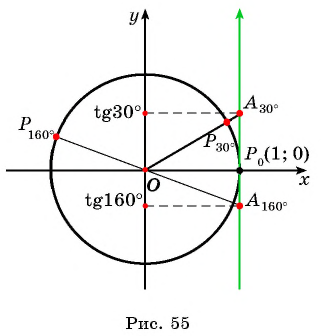
Нахождение тангенса произвольного угла
Для того чтобы найти тангенс произвольного угла а с помощью оси тангенсов, нужно:
- Построить точку
на единичной окружности.
- Продолжить прямую
до пересечения с осью тангенсов.
- Найти ординату точки пересечения прямой
с осью тангенсов.
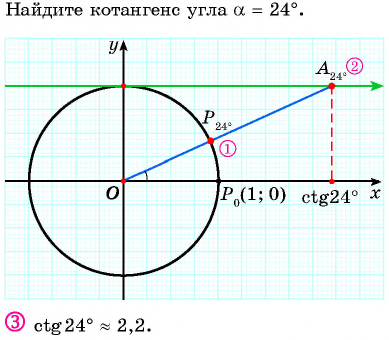
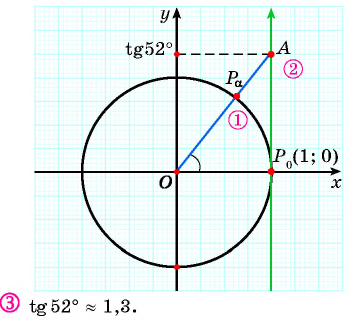
Найдите тангенс угла
Значения тангенса произвольного угла с помощью оси тангенсов можно указать только приближенно. Для нахождения значения тангенса произвольного угла используют четырехзначные таблицы значений тангенса (синуса, косинуса)* или калькулятор. Методы высшей математики позволяют вычислять значения тангенса (синуса, косинуса) с любой заданной степенью точности.
Пример №1
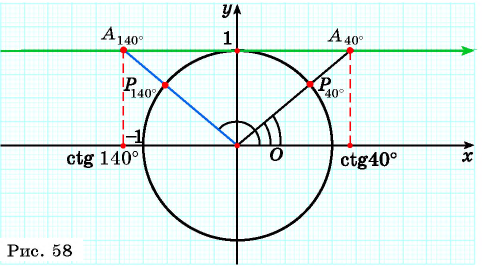
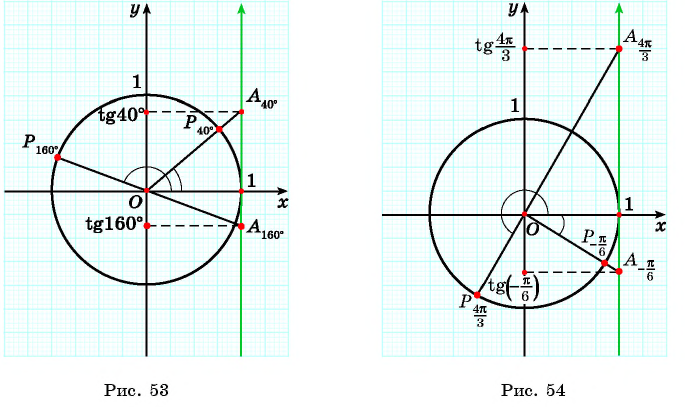
Определите с помощью оси тангенсов:
Решение:
Пример №2
С помощью оси тангенсов сравните значения выражений
Решение:
Отметим на оси тангенсов точки, соответствующие углам 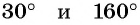
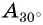
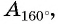
Для углов 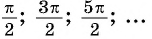
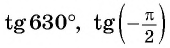
Построим точку 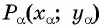
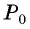
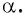
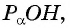
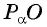
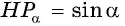
По определению котангенса острого угла получим:
Определение котангенса угла
Определение:
Котангенсом угла 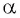
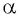
Например,
Поскольку
Воспользуемся полученным равенством и найдем значения котангенсов углов
Поскольку 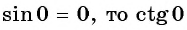
Найденные значения синуса, косинуса, тангенса и котангенса углов 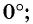
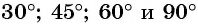
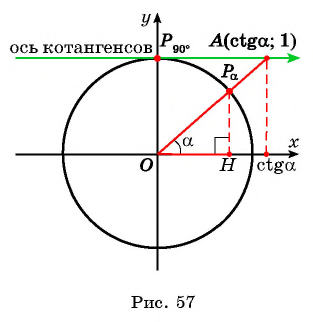
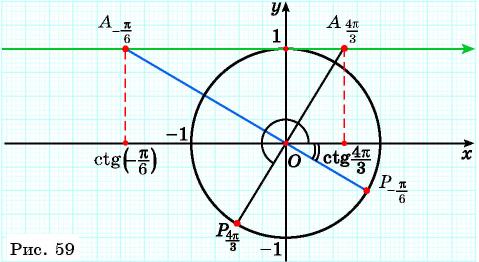
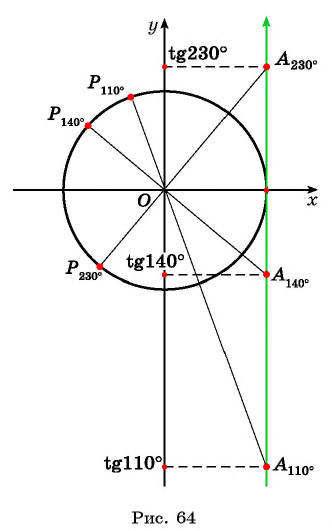
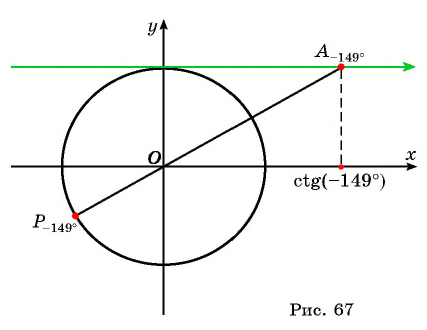
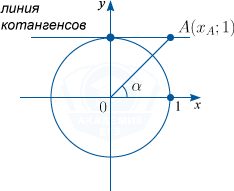
Нахождение котангенса произвольного угла
Для того чтобы найти котангенс произвольного угла 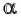
- Построить точку
на единичной окружности.
- Продолжить прямую
до пересечения с осью котангенсов.
- Найти абсциссу точки пересечения прямой
с осью котангенсов.
Значения котангенса произвольного угла с помощью оси котангенсов можно указать только приближенно.
- Заказать решение задач по высшей математике
Пример №3
Найдите значение выражения
Решение:
Через точку 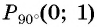
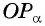
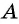
Получим треугольник 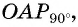
Из подобия треугольников 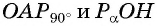
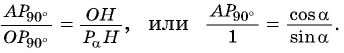
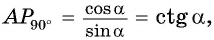
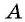
Прямая, перпендикулярная оси ординат, проходящая через точку 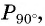
Пример №4
Определите с помощью оси котангенсов:
Решение:
Пример №5
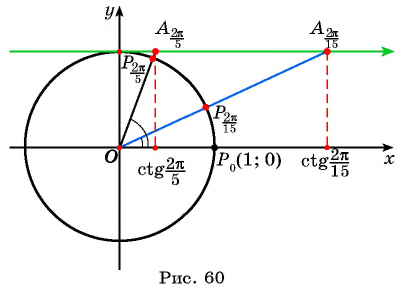
С помощью оси котангенсов сравните значения выражений
Решение:
Отметим на оси котангенсов точки, соответствующие углам 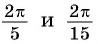
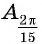
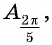
Для углов 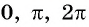
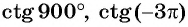
Пример №6
С помощью оси:
а) тангенсов найдите один из углов, тангенс которого равен
б) котангенсов найдите один из углов, котангенс которого равен
Решение:
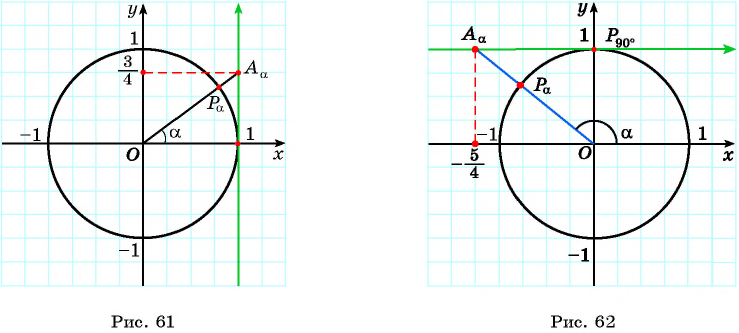
а) 1 Отметим на оси тангенсов точку 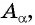
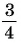
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 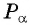
4 Отметим один из углов, соответствующий этой точке (см. рис. 61).
б) 1 Отметим на оси котангенсов точку 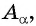
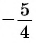
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 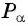
4 Отметим один из углов, соответствующий этой точке (см. рис. 62).
Пример №7
Точка 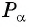
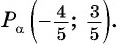
Решение:
Так как точка 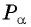
По определению тангенса:
По определению котангенса: 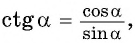
Пример №8
Найдите значение выражения
Решение:
Пример №9
Найдите, если это возможно, значение выражения:
Решение:
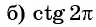
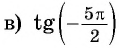
Пример №10
Если 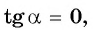
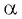
Выберите правильные ответы.
Решение:
Так как тангенсом угла 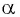
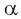
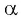
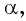
Можно также использовать ось тангенсов: найти точку на оси тангенсов, у которой ордината равна нулю (рис. 63), и определить соответствующие углы. Правильные ответы а) и г).
Пример №11
Расположите в порядке возрастания:
Решение:
Отметим на оси тангенсов точки, соответствующие углам 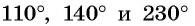
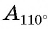
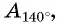
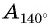
Пример №12
Верно ли, что
Решение:
Отметим на оси котангенсов точки, соответствующие углам 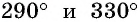
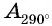
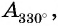
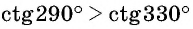
Пример №13
Определите знак выражения:
Решение:
а) Первый способ. По определению тангенса: 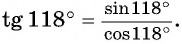
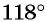
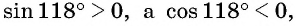
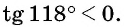
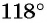
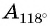
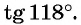
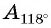
б) Первый способ. По определению котангенса 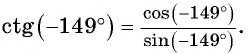
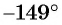
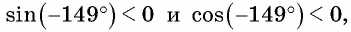
Второй способ. Отметим на оси котангенсов точку, соответствующую углу 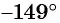
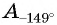
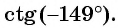
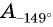
Пример №14
Определите знак произведения
Решение:
Так как угол 3 радиана находится во второй четверти, а угол 4 радиана — в третьей, то 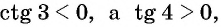
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x – их свойства, графики
- Дробно-рациональные неравенства
- Прогрессии в математике – арифметическая, геометрическая
- Единичная окружность – в тригонометрии
- Определение синуса и косинуса произвольного угла
Что такое котангенс в прямоугольном треугольнике? Как найти котангенс? От чего зависит значение котангенса?
Определение
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

прилежащий катет — АC,
противолежащий катет — BC.
Поэтому котангенс угла A в прямоугольном треугольнике ABC — это

прилежащий катет — BC,
противолежащий — AC.
Поэтому, котангенс угла B в треугольнике ABC
равен отношению BC к AC:
Таким образом, котангенс острого угла прямоугольного треугольника — это некоторое число, получаемое в результате деления длины прилежащего к этому углу катета на длину катета противолежащего.
Так как длины катетов — положительные числа, то и котангенс острого угла прямоугольного треугольника является положительным числом.
Котангенс зависит не от длин катетов, а от их отношения. Для угла определенной величины отношение между катетами, а значит, и значение котангенса, — число постоянное.
Если изменить длины сторон треугольника, но углы оставить без изменения, то котангенсы этих углов не изменятся.

в треугольнике ABC ∠B=30º,
в треугольнике MNK ∠M=30º.
Рассмотрим прямоугольный треугольник ABC.
Синус острого угла прямоугольного треугольника
Отношение противолежащего катета к гипотенузе называют синусом острого угла прямоугольного треугольника.
sin alpha = frac{a}{c}
Косинус острого угла прямоугольного треугольника
Отношение близлежащего катета к гипотенузе называют косинусом острого угла прямоугольного треугольника.
cos alpha = frac{b}{c}
Тангенс острого угла прямоугольного треугольника
Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла прямоугольного треугольника.
tg alpha = frac{a}{b}
Котангенс острого угла прямоугольного треугольника
Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла прямоугольного треугольника.
ctg alpha = frac{b}{a}
Синус произвольного угла
Ордината точки на единичной окружности, которой соответствует угол alpha называют синусом произвольного угла поворота alpha.
sin alpha=y
Косинус произвольного угла
Абсцисса точки на единичной окружности, которой соответствует угол alpha называют косинусом произвольного угла поворота alpha.
cos alpha=x
Тангенс произвольного угла
Отношение синуса произвольного угла поворота alpha к его косинусу называют тангенсом произвольного угла поворота alpha.
tg alpha = y_{A}
tg alpha = frac{sin alpha}{cos alpha}
Котангенс произвольного угла
Отношение косинуса произвольного угла поворота alpha к его синусу называют котангенсом произвольного угла поворота alpha.
ctg alpha =x_{A}
ctg alpha = frac{cos alpha}{sin alpha}
Пример нахождения произвольного угла
Если alpha — некоторый угол AOM, где M — точка единичной окружности, то
sin alpha=y_{M}, cos alpha=x_{M}, tg alpha=frac{y_{M}}{x_{M}}, ctg alpha=frac{x_{M}}{y_{M}}.
Например, если angle AOM = -frac{pi}{4}, то: ордината точки M равна -frac{sqrt{2}}{2}, абсцисса равна frac{sqrt{2}}{2} и потому
sin left (-frac{pi}{4} right )=-frac{sqrt{2}}{2};
cos left (frac{pi}{4} right )=frac{sqrt{2}}{2};
tg left (-frac{pi}{4} right )=-1;
ctg left (-frac{pi}{4} right )=-1.
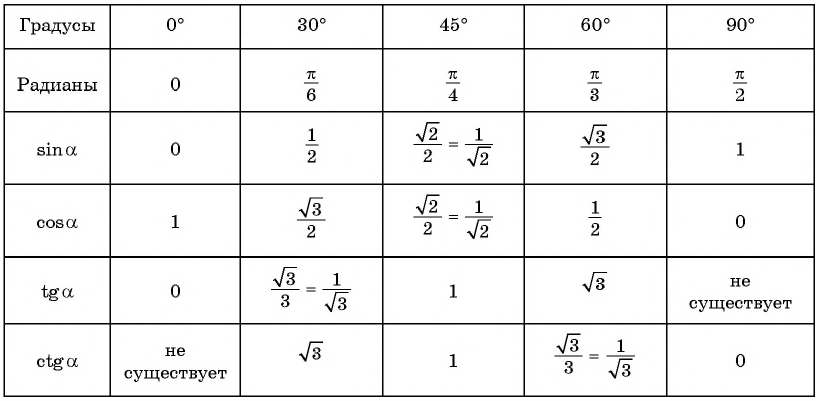
Таблица значений синусов косинусов тангенсов котангенсов
Значения основных часто встречающихся углов приведены в таблице:
| 0^{circ} (0) | 30^{circ}left(frac{pi}{6}right) | 45^{circ}left(frac{pi}{4}right) | 60^{circ}left(frac{pi}{3}right) | 90^{circ}left(frac{pi}{2}right) | 180^{circ}left(piright) | 270^{circ}left(frac{3pi}{2}right) | 360^{circ}left(2piright) | |
| sinalpha | 0 | frac12 | frac{sqrt 2}{2} | frac{sqrt 3}{2} | 1 | 0 | −1 | 0 |
| cosalpha | 1 | frac{sqrt 3}{2} | frac{sqrt 2}{2} | frac12 | 0 | −1 | 0 | 1 |
| tg alpha | 0 | frac{sqrt 3}{3} | 1 | sqrt3 | — | 0 | — | 0 |
| ctg alpha | — | sqrt3 | 1 | frac{sqrt 3}{3} | 0 | — | 0 | — |














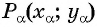
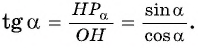
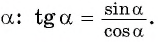
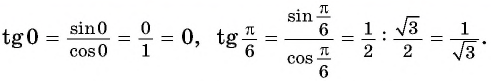
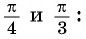
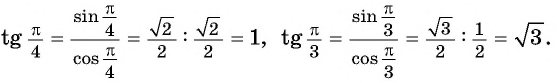
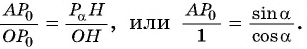
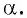
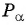 на единичной окружности.
на единичной окружности.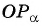 до пересечения с осью тангенсов.
до пересечения с осью тангенсов.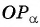 с осью тангенсов.
с осью тангенсов.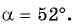

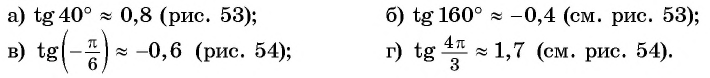
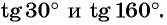
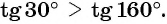
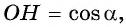
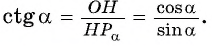
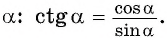
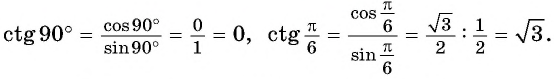
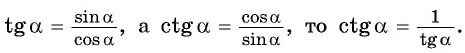
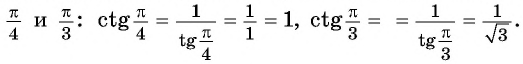
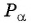 на единичной окружности.
на единичной окружности.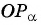 до пересечения с осью котангенсов.
до пересечения с осью котангенсов.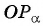 с осью котангенсов.
с осью котангенсов.