Основания равнобедренной трапеции равны 114 и 186. Высота трапеции равна 45. Найдите котангенс острого угла трапеции.
1. Из точки C опустим перпендикуляр на сторону AD. Получится вторая высота CK.
2. Рассмотрим треугольники ABH и DCK. У них AD=CDAD=CD, боковые стороны равнобедренной трапеции равны, ∠BAH=∠CDKangle BAH =angle CDK как углы при основании равнобедренной трапеции. ∠BHA=∠CKD=90∘angle BHA =angle CKD =90 ^{circ} поскольку эти углы образованы перпендикуоярами. Если у нас равны 2 угла, то значит равны и третьи углы, ибо третий угол
∠ABH=180−∠BAH−∠BHAangle ABH = 180-angle BAH – angle BHA
∠DCK=180−∠CDK−∠CKDangle DCK = 180-angle CDK – angle CKD
∠ABH=∠DCKangle ABH = angle DCK
То есть треугольники ABH и DCK равные по двум углам и стороне между ними. Значит AH=KDAH=KD
3. HBCK – правильный прямоугольник.
У него основания BC и AD параллельны, а боковые стороны BH и CK перпендикулярны одному основанию AD, так как это высоты, а значит они параллельны между собой. Значит это параллелограмм. Параллелограмм в котором хотя бы один угол прямой – прямоугольник. У нас даже 2 прямых угла BHK и CKH.
Значит у нас BC=HKBC=HK
AH+HK+KD=ADAH+HK +KD = AD
BC=HKBC=HK
2AH+BC=AD2AH+BC = AD
AH=AD−BC2=186−1142=36displaystyle { AH = frac {AD -BC}{2} = frac {186-114}{2}=36 }
4. В прямоугольном треугольнике ABH нам известны катеты BH=45 и AH=36. Тангенс это отношение противолежащего катета BH к прилежащему AH
tgA=BHAHdisplaystyle { tg A = frac{BH}{AH} }
ctgA=1tgA=AHBHdisplaystyle { ctg A = frac {1}{ tg A} = frac {AH}{ BH} }
ctgA=3645=45=0,8
displaystyle { ctg A = frac {36}{ 45} =frac {4}{ 5}=0,8 }
Задача 59653 В равнобокой трапеции ABCD AB = CD =6…
Условие
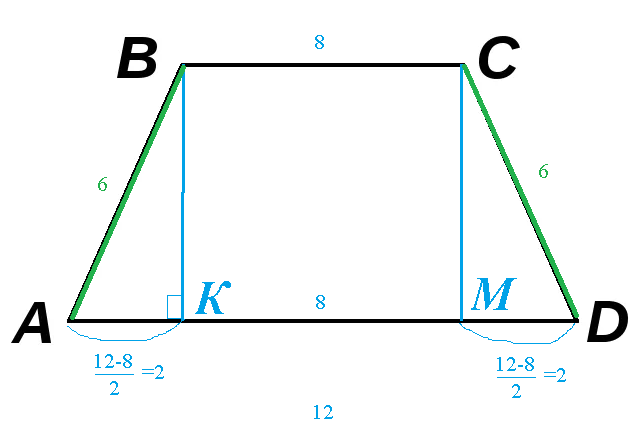
В равнобокой трапеции ABCD AB = CD =6 см, BC = 8 см, AD = 12 см. Найдите синус косинус тангенс и котангенс угла А трапеции
нет в списке
16091
Решение
★
Проводим высоты ВК и СМ на сторону AD
Получаем два равных прямоугольных треугольника
АВК и СМD
AK=MD=(12-8)/2=2
AK=2
ВК^2=AB^2-AK^2=6^2-2^2=36-4=32
BK=sqrt(32)=4sqrt(2)
Из Δ ABK
sin ∠ A=BK/AB=4sqrt(2)/6=2sqrt(2)/3
cos∠ A=AK/AB=2/6=1/3
tg ∠ A=BK/AK=4sqrt(2)/2=2sqrt(2)
Написать комментарий
hededende
Вопрос по геометрии:
В прямоугольной трапеции ABCD(BC||AD,угол а=90 градусов)AB=4см,BC=7см,AD=9см.
Найдите синус,косинус,тангенс и котангенс угла D трапеции
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
ereala513
Решение……………..

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Задание 590
Основание равнобедренного треугольника равно 24 см, а боковая сторона — 13 см. Найдите синус, косинус, тангенс и котангенс угла между боковой стороной треугольника и высотой, проведённой к его основанию.
Ответ:
Дано: Δ АВС — равнобедренный, АВ=ВС=13 см, АС=24 см. ВН — высота.
Найти синус, косинус, тангенс и котангенс ∠АВН.
Рассмотрим ΔАВН — прямоугольный. АН=12 АС=12 см.
ВН=√(13²-12²)=√(169-144)=√25=5 см.
косинус ∠АВН=АН/АВ=1213
синус ∠АВН=ВНАВ=513
тангенс ∠АВН=АНВН=125
котангенс ∠АВН=ВНАН=512.
Задание 591
Боковая сторона равнобедренного треугольника равна 1*^см, а высота, проведённая к основанию, — 8 см. Найдите синус, косинус* тангенс и котангенс угла при основании треугольника.
Ответ:
Дано треугольник АВС, АС = 17 см, ВС = ВС, ВН = 8 см,
Найти углы sin cos tg ctg
Решение
АН = НС = 12 / 2 = 6 см
далее по теореме Пифагора
АВ^2 = AH^2 + BH^2
AB = √36+64 = 8/10 = 10 cм
проведем расчет углов
sin = ВН /АВ = 8/10 = 0,8
cos = 6/10 = 0,6
tg = ВН/АН = 8/6 = 4/3 = 1 1/3
ctg = АН/ВН = 6/8 = ¾
Ответ: 0,8 ,0,6, 1 1/3, ¾
Задание 592
Найдите углы ромба, диагонали которого равны 4 см и 4л/з см.
Ответ:
Дано: АВСД — ромб, АС и ВД — диагонали, АС=4 см, ВД=4√3 см. Найти ∠А, ∠В, ∠С, ∠Д.
Найдем сторону ромба, для этого рассмотрим ΔАОВ — прямоугольный по свойству диагоналей ромба.
По теореме Пифагора АВ²=АО²+ВО²=4+12=16; АВ=√16=4 см.
В ΔАВС АВ=ВС=АС=4 см, значит, ΔАВС — равносторонний, каждый из углов составляет 60°.
∠В=∠Д=60°
∠А+∠С=360-∠В-∠Д=360-120=240°
∠А=∠С=240:2=120°
Ответ: 60°; 120°, 60°, 120°.
Задание 593
Найдите углы между диагональю прямоугольника и его сторонами, длины которых равны л/3 см и 3 см.
Ответ:
ДАНО: АБСД-прямоугольник ас-диагональ. ВС=АД=3, ВА=СД=√3
Найти -угол 1 и угол 2
Решение:tg угла 1 = (отношение вс разделить на ва)= 3 разделить на√3= 3√3 разделить на 3= √3(корень из 3 в таблице это тангенс угла 60 гр) Аналогично :tg угла с= АД разеделить на ДС =3 разделить на √3=3√3 разделить на 3= √3(корень из 3 в таблице это тангенс угла 60 гр),Но нам нужно найти угол 2.значит ,Угол 2= 90-60=30 градусов
Задание 594
В трапеции ABCD известно, что А В = CD = 9 см, ВС = 10 см, AD = 14 см. Найдите синус, косинус, тангенс и котангенс угла А трапеции.
Ответ:
Задание 595
В трапеции ABCD известно, что ВС || AD, ∠А = 90°, АВ — 4 см, ВС = 8 см, AD =12 см. Найдите углы трапеции.
Ответ:
Так как, по условию, угол ВАД = 900, то и угол АВС = 900.
Из вершины С трапеции опустим высоту СН к основанию АД. Длина высоты равна длине стороны АВ. СН = АВ = 4 см.
Высота СН отсекает на основании АД два отрезка, один из которых равен основанию ВС, так как АВСД прямоугольник, а его противоположные стороны равны. АН = ВС = 8 см.
Тогда отрезок ДН = АД – АН = 12 – 8 = 4см.
Прямоугольный треугольник СНД равнобедренный, так как СН = ДН = 4 см, тогда его углы при основании СД равны 450.
Угол АДС = НДС = 450, тогда угол ВСД = ВСН + НСД = 90 + 45 = 1350.
Ответ: Углы трапеции равны: 900, 900, 1350 и 450.
Задание 596
Докажите, что тангенсы острых углов прямоугольного треугольника являются взаимно обратными числами.
Ответ:
tg (C) = AB/BC
tg (A) = BC/AB
tg (A) = BC/AB = 1/AB/BC = 1/tg(C) = 1/x
Задание 597
Докажите тождество: 1) 1 + tg2 а = 1/cos2a; 2) 1 + ctg2 а = 1/sin2a
Ответ:
tg — отношение синуса к косинусу, получаем:
1+sin^2a/cos^2a=1/cos^2a
приводим к общему знаменателю левую часть:
сos^2a/cos^2a + sin^2a/cos^2a = 1/cos^2a cos^2a+sin^2a/cos^2a = 1/cos^2a
по основному тригонометрическому тождеству раскладываем единицу: соs^2a+sin^2a/cos^2a=sin^2a+cos^2a/cos^2a
сворачиваем квадраты синусов и косинусов:
1/cos^2a=1/cos^2a
Задание 598
Найдите значение выражения: 1) sin2 18° + sin2 72°; 2) cos3 36° — sin3 54°.
Ответ:
1) sin² (18°) + sin² (72²) = cos² (72°) + sin² (72°)
sin²β + cos²β = 1
cos² (72°) + sin² (72°) = 1
2) sin³ (54°) – sin³ (90° – 36°) = cos³ (36°)
cos³ (36°) – sin³ (54°) = cos³ (36°) – cos³ (36°) = 0
Задание 599
Катеты прямоугольного треугольника равны 30 см и 40 см. Найдите синус, косинус, тангенс и котангенс угла между медианой и высотой, проведёнными к гипотенузе.
Ответ:
Катеты прямоугольного треугольника равны 30 см и 40 см. Найдите синус, косинус, тангенс, котангенс угла между медианой и высотой, проведенных к гипотенузе.
Пусть дан треугольник АВС. ВС=30 см, АС=40 см. Из отношения катетов 3:4 следует, что этот треугольник — египетский, и АМ=50 см ( по т. Пифагора, естественно, также АВ=50 см)
Длина медианы прямоугольного треугольника из прямого угла к гипотенузе равна ее половине. ⇒ СМ=ВМ=АМ=25 см ∆ АМС — равнобедренный.
Высота прямоугольного треугольника делит его на подобные треугольники.
∆ ВНС~∆ ВСН, коэффициент подобия k= ВС:АВ=0,6 ⇒
ВН=СН*0,6=18 см
СН=АС*0,6=24 см
МН=ВМ-ВН=25-18=7 см
sin ∠HCM=MH:CM=7/25
cos ∠HCM=CH:CM=24/25
tg ∠HCM=HM:HC=7/24
ctg ∠HCM=HC:HM=24/7
Задание 600
В треугольнике ABC известно, что АВ = ВС, BD и AM — высоты треугольника, BD : AM = 3:1. Найдите cos С.
Ответ:
sin (A) = BD/AB = 3x/AB
sin (C) = BD/BC = 3x/AB, так как AB = BC
3x/AB = 1x/AC,
AC/AB = 1x/3x, тогда
AC = 1x, a AB = 3x
AD = DC = ½AC = ½x
cos (C() = DC/BC = ½ ̶x̶/3 ̶x̶ = 1/6
Задание 601
В треугольнике ABC известно, что АВ -ВС, BD и СК — высоты треугольника, cos А = — . Найдите отношение СК : BD.
Ответ:
1) S=1/2*AC*BD; S=1/2*AB*CK ===> AC*BD=AB*CK ===> CK/BD = AC/AB. 2) AD/AB=cosA; AB=AD/(3/7)=7AD/3. 3) AD=AC/2, т. к. высота в равнобедренном тр-ке является и медианой. AC=2AD. СK/BD = 2AD /(7AD/3); CK/BD =2AD*3/7AD=6/7; CK:BD=6:7
Задание 602
Докажите, что углы ABC и DEF, изображённые на рисунке 184, равны.
Ответ:
Задание 603
Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке М, АВ = б см. Найдите радиус окружности, которая проходит через точки А, В и М.
Ответ:
AD=8 см
т.к. М1ВМ2С — прямоугольник, т.к угол АВМ1+КВМ2 = М2ВС+ СВМ1, а сумма всех этих углов = 180 град (развернутый угол, т.е. М1ВМ2 =90 град.
Так же докажем, что М1СМ2= 90 град..
В прямоугольнике диагонали равны, т.е. М1М2=ВС = 8см
В параллелограмме параллельные стороны равны, т.е AD=ВС=8 см
В равнобокой трапеции ABCD AB = cd = 6 BC = 8 Ad = 12 найти синус косинус и тангенс угла A.
На этой странице находится вопрос В равнобокой трапеции ABCD AB = cd = 6 BC = 8 Ad = 12 найти синус косинус и тангенс угла A?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 10 – 11 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.












