Как найти ковариацию по таблице

Двумерной называют случайную величину

, возможные значения
которой есть пары чисел

. Составляющие

 и

, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку

 на плоскости

 либо как случайный вектор

.

Дискретной называют двумерную величину, составляющие которой дискретны.

Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих

Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.

Закон
распределения дискретной двумерной случайной величины может быть задан:

а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;

б) аналитически, например в виде функции распределения.

Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность

, надо просуммировать
вероятности столбца

. Аналогично сложив
вероятности строки

 получим вероятность

.

Пусть
составляющие

 и

 дискретны и имеют соответственно следующие
возможные значения:

; 

.

Условным распределением составляющей

 при

 (j сохраняет одно и то же
значение при всех возможных значениях

) называют совокупность
условных вероятностей:

Аналогично
определяется условное распределение

.

Условные
вероятности составляющих

 и

 вычисляют соответственно по формулам:

Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.

Ковариация (корреляционный момент)

Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки

.

Ковариацию
(корреляционный момент) можно найти по формуле:

Свойства ковариации

Свойство 1.

Ковариация двух независимых случайных величин равна нулю.

Свойство 2.

Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.

Свойство 3.

Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.

Коэффициент корреляции

Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.

Формула коэффициента корреляции:

Две
случайные величины

 и

 называют коррелированными, если их коэффициент
корреляции отличен от нуля.

 и

 называют некоррелированными величинами, если
их коэффициент корреляции равен нулю

Свойства коэффициента корреляции

Свойство 1.

Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.

Свойство 2.

Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.

Свойство 3.

Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.

Линейная регрессия

Рассмотрим
двумерную случайную величину

, где

 и

 – зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины

 в виде линейной функции величины

:

где

 и

 – параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.

Линейная
средняя квадратическая регрессия

 на

 имеет вид:

Коэффициент

называют
коэффициентом регрессии

 на

, а прямую

называют
прямой среднеквадратической регрессии

 на

.

Аналогично
можно получить прямую среднеквадратической регрессии

 на

:

Смежные темы решебника:

• Двумерная непрерывная случайная величина
• Линейный выборочный коэффициент корреляции
• Парная линейная регрессия и метод наименьших квадратов

Задача 1

Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.

Требуется:

–
определить одномерные законы распределения случайных величин X и Y;

– найти
условные плотности распределения вероятностей величин;

–
вычислить математические ожидания m_x и m_y;

–
вычислить дисперсии σ_x и σ_y;

–
вычислить ковариацию μ_xy;

–
вычислить коэффициент корреляции r_xy.

xy	3	5	8	10	12
-1	0.04	0.04	0.03	0.03	0.01
1	0.04	0.07	0.06	0.05	0.03
3	0.05	0.08	0.09	0.08	0.05
6	0.03	0.04	0.04	0.06	0.08

---

Задача 2

Задана
дискретная двумерная случайная величина (X,Y).

а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X;  в) построить регрессию случайной величины X на Y;  г) найти коэффициент ковариации; д) найти
коэффициент корреляции.

Y	X
1	2	3	4	5
30	0.05	0.03	0.02	0.01	0.01
40	0.03	0.02	0.02	0.04	0.01
50	0.05	0.03	0.02	0.02	0.01
70	0.1	0.03	0.04	0.03	0.01
90	0.1	0.04	0.01	0.07	0.2

---

Задача 3

Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.

x y	1	2	3
1.5	0.03	0.02	0.02
2.9	0.06	0.13	0.03
4.1	0.4	0.07	0.02
5.6	0.15	0.06	0.01

---

Задача 4

Двумерная
случайная величина (X,Y) распределена по закону

XY	1	2
-3	0,1	0,2
0	0,2	0,3
-3	0	0,2

Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.

---

Задача 5

Случайные
величины ξ и η имеют следующий совместный закон распределения:

P(ξ=1,η=1)=0.14

P(ξ=1,η=2)=0.18

P(ξ=1,η=3)=0.16

P(ξ=2,η=1)=0.11

P(ξ=2,η=2)=0.2

P(ξ=2,η=3)=0.21

1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.

2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).

3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}

4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.

---

Задача 6

Дан закон
распределения двумерной случайной величины (ξ,η):

	ξ=-1	ξ=0	ξ=2
η=1	0,1	0,1	0,1
η=2	0,1	0,2	0,1
η=3	0,1	0,1	0,1

1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания M_ξ,
M_η и дисперсии D_ξ, D_η

2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).

3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?

4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти M_γ  и D_γ.

---

Задача 7

Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.

XY	1	2	4
-2	0,25	0	0,25
1	0	0,25	0
3	0	0,25	0

---

Задача 8

Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.

YX	-1	1
-1	0,4	0,1
1	0,2	0,3

---

Задача 9

Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:

	X=-3	X=0	X=1
Y=-2	0,3	?	0,1
Y=1	0,1	0,1	0,2

---

Задача 10

Совместный
закон распределения пары

 задан таблицей:

xh	-1	0	1
-1	1/12	1/4	1/6
1	1/4	1/12	1/6

Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.

---

Задача 11

Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции r_xy?

X	20	25	30	35
P	0.1	0.1	0.4	0.4

и

---

Задача 12

Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):

XY	0	1	2
-1	?	0,1	0,2
1	0,1	0,2	0,3

---

Задача 13

Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:

ξη	-1	1	2
0	1/7	2/7	1/7
1	1/7	1/7	1/7

Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?

---

Задача 14

Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.

XY	2,3	2,9	3,1	3,4
0,2	0,15	0,15	0	0
2,8	0	0,25	0,05	0,01
3,3	0	0,09	0,2	0,1

---

Задача 15

Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.

xy	1	4
-10	0,1	0,2
0	0,3	0,1
20	0,2	0,1

---

Задача 16

Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:

а) законы
распределения ее компонент и их числовые характеристики;

b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.

с)
ковариацию и коэффициент корреляции случайных величин X и Y;

d) составить матрицу ковариаций и матрицу корреляций;

e) вероятность попадания в область, ограниченную линиями y=16-x² и y=0.

f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.

XY	-1	0	1	2
-1	0	1/6	0	1/12
0	1/18	1/9	1/12	1/9
2	1/6	0	1/9	1/9

---

Задача 17

Совместный
закон распределения случайных величин X и Y задан таблицей:

XY	0	1	3
0	0,15	0,05	0,3
-1	0	0,15	0,1
-2	0,15	0	0,1

Найдите:

а) закон
распределения случайной величины X и закон распределения
случайной величины Y;

б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.

---

Задача 18

Известен
закон распределения двумерной случайной величины (X,Y).

а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);

б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;

в)
построить поле распределения и линию регрессии Y по X и X по Y;

г)
вычислить корреляционный момент (коэффициент ковариации) μ_xy и
коэффициент корреляции r_xy.

	5	20	35
100	—	—	0.05
115	—	0.2	0.15
130	0.15	0.35	—
145	0.1	—	—-

Функция КОВАРИАЦИЯ.В в Excel предназначена для расчета коэффициента ковариации двух наборов данных (массивов или диапазонов ячеек, хранящих числовые значения), являющихся выборками соответствующих диапазонов данных, и возвращает соответствующее числовое значение.

Функция КОВАРИАЦИЯ.Г в Excel используется для расчета коэффициента ковариации всей совокупности двух диапазонов данных (генеральной совокупности) и возвращает соответствующее значение.

Функция КОВАР в Excel предназначена для расчета коэффициента ковариации двух любых наборов числовых данных, являющихся генеральными совокупностями.

Использование функций КОВАР, КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г в Excel

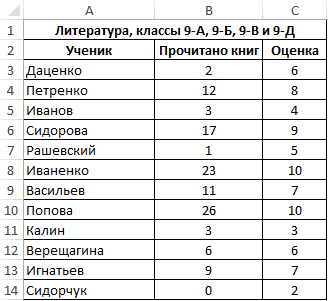
Пример 1. В таблице Excel содержится два диапазона данных, значения первого из которых характеризуют количество прочитанных книг за год каждым учеником, отобранным из нескольких классов школы, а второй – итоговую оценку по литературе по 10-бальной шкале. Определить коэффициент ковариации двух диапазонов данных.

Вид исходной таблицы:

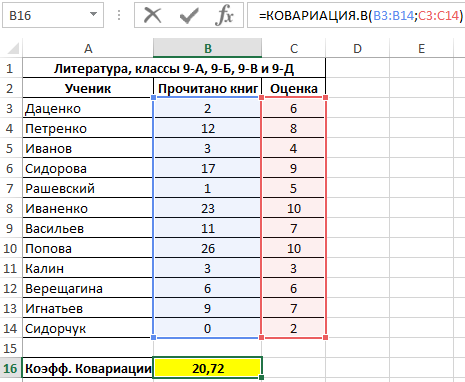
Поскольку для анализа были отобраны по несколько учеников различных классов, оба диапазона можно считать выборками из генеральной совокупности, которой являются все ученики 9-го класса данной школы. Используем следующую функцию:

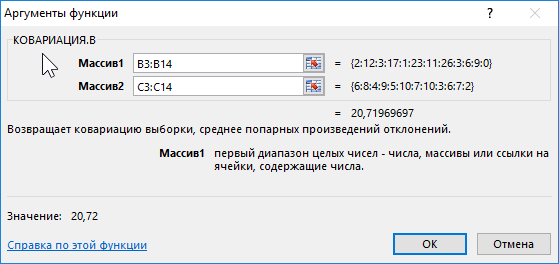
Описание аргументов:

• B3:B14 – диапазон ячеек, содержащих данные о количестве прочитанных книг;
• C3:C14 – диапазон ячеек с итоговыми оценками по предмету.

Полученный результат:

Полученное значение свидетельствует о наличии прямой связи между значениями из двух диапазонов. То есть, можно полагать, что ученик, прочитавший большее количество книг, получит более высокую оценку за предмет.



Расчет ковариации роста и падения цен двух видов акций в Excel

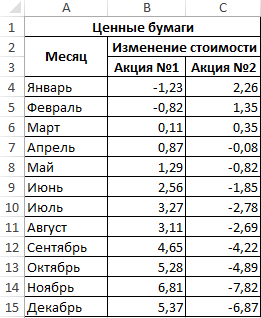
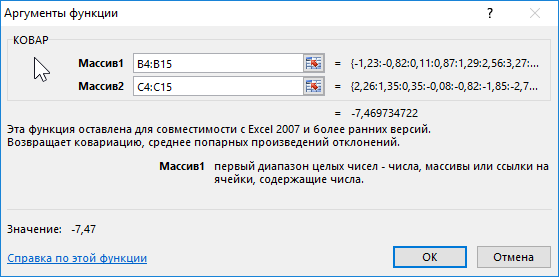
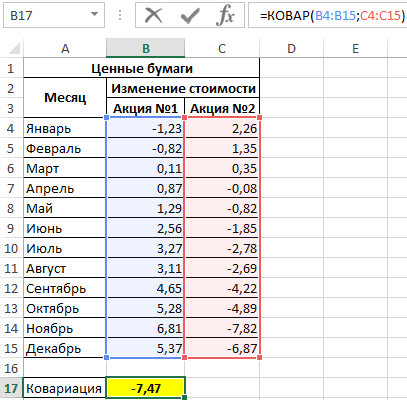
Пример 2. В таблице Excel внесены данные роста (положительное число) или падения цены (отрицательное) двух различных ценных бумаг на протяжении 12 месяцев года относительно некоторой начальной величины. Определить ковариацию двух диапазонов данных и сделать выводы. Сделать отчет доступным для пользователей Excel 2007.

Вид исходной таблицы:

В данном примере исследуется вся генеральная выборка. Для расчета можно использовать функцию КОВАРИАЦИЯ.Г, однако результаты не будут доступны для пользователей более старых версий Excel. Применим следующую формулу:

В результате получим:

Это значение свидетельствует о достаточно большой взаимосвязи между исследуемыми значениями. Поскольку число отрицательное, данная взаимосвязь является обратной. То есть, с ростом цены одной акции наблюдается падение цены второй и наоборот. Можно предположить, что эти акции принадлежат двум конкурирующим компаниям.

Статистический анализ ковариации показателей в Excel

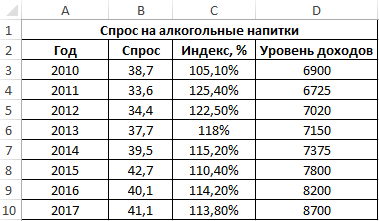
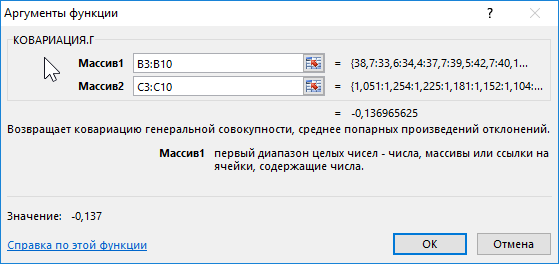
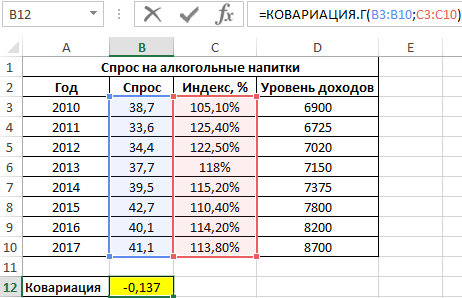
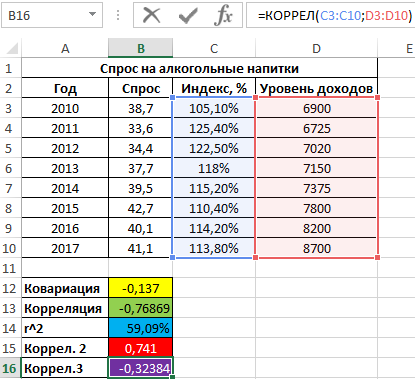
Пример 3. В таблице Excel введены данные о спросе на алкогольные напитки, индексе цен и уровне дохода населения государства. Проанализировать взаимосвязи между имеющимися данными.

Вид исходной таблицы данных:

Вначале рассчитаем ковариацию между спросом и индексом цен по формуле:

Полученный результат:

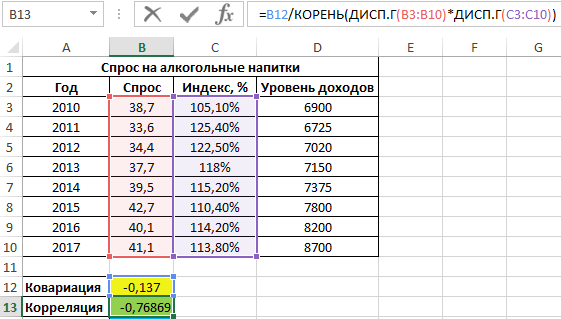
Для оценки степени взаимосвязи двух диапазонов данных удобнее использовать коэффициент корреляции, который можно рассчитать без использования функции КОРРЕЛ следующим способом:

=B12/КОРЕНЬ(ДИСП.Г(B3:B10)*ДИСП.Г(C3:C10))

Функция ДИСП.Г используется для расчета дисперсии генеральной совокупности. Приведенная выше формула наглядно демонстрирует взаимосвязь между коэффициентами ковариации и корреляции.

Полученный результат:

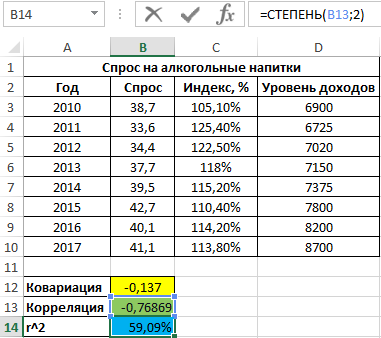
Как видно, между ценами и спросом существует довольно сильная обратная связь. Однако для определения степени влияния спроса определим коэффициент детерминации r2 по формуле:

=СТЕПЕНЬ(B13;2)

Полученное значение, выраженное в процентах:

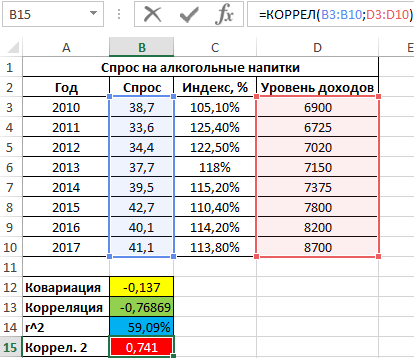
То есть, примерно 59% вариации спроса за исследуемый период обусловлены изменчивостью цены. Остальные 41% – прочими факторами. А еще одним фактором в данном примере является уровень дохода. Рассчитаем коэффициент корреляции между спросом и доходами с помощью следующей функции:

=КОРРЕЛ(B3:B10;D3:D10)

Результат:

Положительное значение 0,741 соответствует о наличии довольно сильной зависимости между ростом уровня доходов и спросом. Чтобы определить общий коэффициент корреляции и сделать выводы, найдем коэффициент корреляции между индексом цен и уровнем доходов:

=КОРРЕЛ(C3:C10;D3:D10)

Результат:

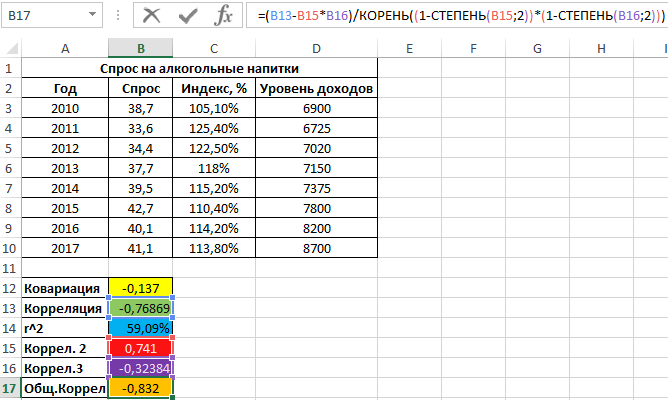
Имеем не сильно выраженную обратную взаимосвязь. Теперь выполним расчет общего коэффициента корреляции по формуле:

=(B13-B15*B16)/КОРЕНЬ((1-СТЕПЕНЬ(B15;2))*(1-СТЕПЕНЬ(B16;2)))

Результат:

Расчеты показывают, что влияние роста цен на уровень спроса «сглаживается» благодаря росту уровня дохода населения. Корень квадратный из последнего значения, взятого по модулю, равен примерно 91%, показывая, насколько вариация цен определяла вариация спроса на алкогольные напитки, если не брать в учет параллельное изменение уровня дохода.

Особенности использования функций КОВАР, КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г в Excel

Функция КОВАР имеет следующий синтаксис:

= КОВАР(массив1;массив2)

Функция КОВАРИАЦИЯ.В имеет следующую синтаксическую запись:

= КОВАРИАЦИЯ.В(массив1;массив2)

Синтаксис функции КОВАРИАЦИЯ.Г:

= КОВАРИАЦИЯ.Г(массив1;массив2)

Все рассматриваемые функции принимают на вход следующие аргументы:

• массив1 – обязательный аргумент, характеризующий первый массив или диапазон ячеек, содержащих данные числового типа, которые являются всей генеральной совокупностью данных (для функций КОВАРИАЦИЯ.Г и КОВАР) или выборкой (для функции КОВАРИАЦИЯ.В);
• массив2 – обязательный аргумент, характеризующий второй массив или диапазон ячеек с числовыми значениями (генеральная совокупность либо выборка, чем обусловлен выбор функции для расчета).

Примечания 1:

1. Все рассматриваемые функции принимают в качестве аргументов массивы или ссылки на диапазоны ячеек, содержащие текстовые, логические, числовые и данные других типов.
2. Число элементов в диапазонах или массивах, переданных в качестве аргументов массив1 и массив2 должны совпадать. В противном случае все рассматриваемые функции вернут код ошибки #Н/Д.
3. При расчете не учитываются значения типа Текст, Имя, логические значения (ИСТИНА, ЛОЖЬ), ссылки на пустые ячейки. Однако ячейки, содержащие числовое значения 0 (нуль), будут учтены.
4. Если рассматриваемые функции в качестве аргументов принимают:

• Диапазоны пустых ячеек, результатом их выполнения будет код ошибки #ЗНАЧ! (принимают по одной пустой ячейке в качестве каждого аргумента) или #ДЕЛ/0! (принимают по несколько пустых ячеек в качестве аргументов);
• Массивы, состоящие из одного элемента или по одной ячейке в качестве каждого аргумента, функции КОВАРИАЦИЯ.Г и КОВАР вернут числовое значение 0, а функция КОВАРИАЦИЯ.В – код ошибки #ДЕЛ/0!.

Примечания 2:

1. Ковариация – величина, характеризующая линейную зависимость, установившуюся между двумя рядами случайных величин X и Y. Она соответствует математическому ожиданию произведения отклонений X и Y от их центров распределений. Коэффициент ковариации может быть выражен отрицательным, положительным числами и нулем, при этом:

• Если с ростом значений X более вероятные появления больших значений Y и наоборот, между двумя диапазонами существует прямая связь, о чем свидетельствует положительное значение коэффициента ковариации;
• Если с ростом X величина Y имеет тенденцию к снижению и наоборот, устанавливается обратная зависимость, выражаемая отрицательным значением коэффициента ковариации;
• Если между X и Y устанавливается слабая взаимосвязь (при изменениях X изменения Y являются непоследовательными, хаотичными), значение коэффициента ковариации стремится к нулю.

Примечания 3:

1. Функция КОВАР являлась стандартной функцией для расчета ковариации в ранних версиях Excel (2007 и более старых) и оставлена для обеспечения совместимости. В последующих версиях Excel она может отсутствовать, поэтому рекомендуется использовать функции КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г.
2. Выборка – это подмножество величин одного множества, называемого генеральной совокупностью. Другими словами, выборкой считается результат ограниченного ряда наблюдений какого-либо одно или нескольких признаков. Например, при изучении банковской системы государства генеральной совокупностью являются все банковские организации страны, а выборкой – банки города Санкт-Петербург.
3. В отличие от коэффициента корреляции, значение коэффициента ковариации не ограничено диапазоном чисел от -1 до 1.
4. При определении коэффициента ковариации одних и тех же двух диапазонов чисел функции КОВАР и КОВАРИАЦИЯ.Г вернут одинаковый результат, отличающийся от числового значения, которое вернет функция КОВАРИАЦИЯ.В, поскольку они используют разные алгоритмы расчетов.

Ковариация

_{Характеристикой
зависимости между случайными величинами
X
и Y
служит математическое ожидание
произведения отклонений X
и Y от их
центров распределений (так иногда
называют математическое ожидание
случайной величины), которое называется
коэффициентом ковариации или просто
ковариацией.}

_{Cov(X;Y) = E((X–EX)(Y–EY))}

_{Пусть
X = x1,
x2,
x3,,
xn,
Y= y1,
y2,
y3,,yn.
Тогда}

_Cov(X;Y)=

_{Эту
формулу можно интерпретировать так.
Если при больших значениях Х
более вероятны большие значения Y,
а при малых значениях X
более вероятны малые значения Y,
то в правой части формулы ковариации
положительные слагаемые
доминируют, и ковариация принимает
положительные значения.}

_{Если
же более вероятны произведения
(xi – EX)(yj – EY),
состоящие из сомножителей разного
знака, то есть исходы случайного
эксперимента, приводящие к большим
значениям X
в основном приводят к малым значениям
Y и наоборот,
то ковариация принимает большие по
модулю отрицательные значения.}

_{В
первом случае принято говорить о прямой
связи: с ростом X
случайная величина Y
имеет тенденцию к возрастанию.}

_{Во
втором случае говорят об обратной связи:
с ростом X
случайная величина Y
имеет тенденцию к уменьшению или падению.}

_{Если
примерно одинаковый вклад в сумму дают
и положительные и отрицательные
произведения (xi – EX)(yj – EY)pij,
то можно сказать, что в сумме они будут
“гасить” друг друга и ковариация будет
близка к нулю. В этом случае не
просматривается зависимость одной
случайной величины от другой.}

_{Легко
показать, что если}

_{P((X = xi)∩(Y = yj)) = P(X = xi)P(Y = yj)
(i = 1,2,,n;
j = 1,2,,k),}

_{то
cov(X;Y)=
0.}

_{Действительно
из (2) следует}

_{Здесь
использовано очень важное свойство
математического ожидания: математическое
ожидание отклонения случайной величины
от ее математического ожидания равно
нулю.}

_{Ковариацию
удобно представлять в виде}

_{Cov(X;Y)=E(XY–XEY–YEX+EXEY)=E(XY)–E(XEY)–E(YEX)+E(EXEY)=}

_{=E(XY)–EXEY–EXEY+EXEY=E(XY)–EXEY}

_{Ковариация
двух случайных величин равна математическому
ожиданию их произведения минус
произведение математических ожиданий.}

_{Поскольку
для независимых случайных величин EXY
= EXEY,
то, очевидно, что для
независимых случайных величин X
и Y cov(X;Y)=0.}

Определение.
Случайные величины, ковариация которых
равна нулю, называют некоррелированными.

!!!
Замечание.
Как было
показано выше, из независимости случайных
величин следует их некоррелированность,
то есть равенство нулю корреляции.
Обратное
неверно! Рассмотрим
соответствующий пример:

Пусть
случайная величина Х имеет равномерное
распределение на интервале (-1, 1), а
случайная величина Y
связана со случайной величиной Х
функциональной зависимостью Y=X²
. Покажем, что cov
(X,Y)=0,
хотя налицо функциональная зависимость
.

Учитывая
, что ЕХ=0 (середина интервала (-1,1)),
получаем:

cov
(X,Y)=EXY-EXEY=EX³
=

Итак,
из некоррелированности случайных
величин не следует их независимость.

Ковариация
случайных величин отражает степень
близости зависимости случайных величин
к линейной, то есть, к зависимости вида
Y=aX+b.

Рассмотрим
теперь еще одну меру линейной зависимости
– коэффициент
корреляции
случайных величин Х и Y
r(X,Y)
=

Может
возникнуть вопрос, зачем вводить еще
одну меру линейной зависимости?

1. Коэффициент
   корреляции меняется от -1 до 1, а не по
   всей числовой оси

2. Коэффициент
   корреляции, в отличие от ковариации,
   нечувствителен к смене единиц измерения

3. Если
   случайные величины независимы, то
   коэффициент корреляции, как и ковариация,
   равен нулю.

4. Если
   случайные величины линейно зависимы,
   то r=1
   – прямая зависимость , r=-1,
   обратная. И наоборот, из равенства по
   модулю 1 следует линейная зависимость.

Пусть
распределение случайных величин задано
таблицей

ЕХ₁

ЕХ₂

DX₁
= EX₁
²
– (EX₁)²=
0,59

DX₂
= EX₂
²
– (EX₂)²=
0,2475

Cov
(X₁
,X₂
)= E (X₁
,X₂
)–E X₁
EX₂

E
(X₁
,X₂
) =

Замечание.
Ковариационная и корреляционная матрицы
– это таблицы, состоящие соответственно
из ковариаций и коэффициентов корреляций
соответствующих случайных величин.
(Заметим, что по главной диагонали
корреляционной матрицы стоят 1 –
случайная величина, очевидно, находится
сама с собой в линейной зависимости).
Используются эти матрицы для наглядного
представления данных о связи величин
и в статистике.

Соседние файлы в папке Модуль 1. Лекции

• #
• #
• #
• #
• #
• #
• #