Как найти кпд аккумулятора

Суммарный
КПД регулятора заряда и аккумулятора
составляет 83.06 процентов (см. п. 3.2).
Определить КПД каждого из этих устройств
мы сможем при начальной стадии заряда,
так как время зарядки аккумулятора в
эксперименте 1 час, а для того чтобы
зарядить его на 100 процентов потребуется
около 2-х суток, при таком же значении
мощности, выдаваемой солнечной батареей.

Значение тока до регулятора заряда
и после него совпадают в течении всего
эксперимента, а значения напряжения
несколько отличаются:

U_{н
рег зар} = 12.84 В,

U_{н
аккум} = 12.54 В,

U_{к
рег зар} = 13.4 В,

U_{к
аккум} = 13.05 В.

Значения
напряжения на аккумуляторе начальное
и конечное снимаются при включенном
токе зарядки. Вычислим разницу начальных
и конечных напряжений на аккумуляторе
и регуляторе заряда, затем найдём среднее
значение просадки напряжения на
контроллере заряда.

ΔU_н
= 12.84 – 12.54 = 0.3В,

ΔU_к
= 13.4 – 13.05 = 0.35В,

ΔU_{среднее}
= (0.35 + 0.3) = 0.325В.

Среднее
значение тока, поступающего на контроллер
заряда, равно:
I_{среднее}
= 159 мА.

Перемножив просадку напряжения на
контроллере заряда на среднее значение
тока, получим потерю мощности на
контроллере заряда:

	ΔW = ΔUсреднее *Iсреднее	(3.2)
	ΔW = 0.159*0.325

ΔW
= 0.0517 Вт.

Посчитаем
КПД регулятора заряда по формуле 3.3:

(3.3)

где ΔW,
[Вт] определяем из формулы 3.2, W₀,
[Вт] – мощность, поступающая на регулятор
заряда (см. табл. 3.1).

Смысл
выражения 3.3 состоит в том, что КПД
регулятора заряда определяется как
отношение мощности на выходе с регулятора
заряда к отношению мощности, поступающей
на его вход.

η_рег
= 0.975 = 97.5%

Реальный
КПД регулятора заряда несколько ниже.
Новейшие контроллеры заряда могут
работать в режиме отслеживания точки
максимальной мощности солнечной батареи
– MPPT
контролеры, что ещё могло бы увеличить
общий КПД установки.

Определим
КПД аккумулятора как частное КПД
аккумулятора и контролера заряда и КПД
контролера в отдельности:

η_аккум
= 0.8306/0.975 = 0.8519 = 85.19%

Проверим
суммарные расчёты КПД для всех устройств:
произведение кпд всех устройств должно
равняться суммарному КПД всей установки
без солнечной батареи:

ηуст. = ηрег.зар.* ηаккум.* ηинвер.

(3.4)

η_{рег.зар.}
= 97.5%

η_аккум.
= 85.19%

η_инвер.
= 89.05%

ηуст. = 0.975*0.8519*0.8905

η_уст.
= 0.7396 = 73.96%

Проверка
показывает, что расчёт КПД всех элементов
установки выполнен верно, так как
произведение КПД отдельных устройств
в установке равно суммарному КПД без
солнечной батареи.

3.4. Определение суммарного кпд всей системы

Определим
общий КПД всей установки, включая
солнечную батарею, регулятор заряда,
аккумулятор и инвертор по формуле 3.5:

ηобщ.уст. = ηуст.* ηсолн.бат.

(3.5)

где η_уст
определим по формуле 3.4, а η_{солн.бат.}
берём из п.2.3.2 для стандартного значения
напряжения питания ламп в 220В.

η_{солн.бат.}
= 8.04% = 0.0804

η_уст.
= 73.96% = 0.7396

ηобщ.уст. = 0.0804*0.7396

η_{общ.уст.}
= 0.0595 = 5.95%

Вывод:
общий КПД всего цикла производства
электроэнергии составляет около 6
процентов. С одной стороны этот показатель
невысок, однако, принцип действия
автономной солнечной электростанции
сводится к тому, что она в течении всего
светового дня накапливает энергию(около
10-12 часов) и отдаёт энергию в течении
двух-трёх часов в тёмное время суток.
Поэтому реальная эффективность данного
цикла производства электроэнергии
выше, чем 6 процентов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Тут недавно в комментах на ютьюбе прицепился ко мне немного странный товарищ, который пытался меня уверить, что ни в коем случае нельзя использовать «связку» солнечной батареи и буферного аккумулятора 🙂 Поскольку, по его версии, в аккумуляторе теряется 30-40% энергии — прямо вот ужас-ужас! Я-то, с младых ногтей, помню про совсем иную цифру для литиевых аккумуляторов: примерно 3-5% потерь, т.е. на порядок меньше 🙂

Но все же, малость «завел» он меня — так что я поставил небольшой эксперимент. Задача простая: нужно померить КПД аккумулятора, или иными словами, посчитать разницу между энергией, израсходованной на зарядку аккумулятора и той энергией, которую мы можем потом из этого аккумулятора получить обратно.

Проще всего подобный замер было сделать с помощью универсального зарядника iMax, поскольку он умеет как заряжать, так и разряжать аккумуляторы, и при этом еще показывает, сколько в аккумулятор ушло, и сколько мы от него получили.

В общем, я взял аккумулятор, разрядил его (iMax разряжает до напряжения 3В, что меня для целей данного эксперимента вполне устраивает), потом полностью зарядил и снова разрядил. Результаты представлены на фото.

В сухом остатке имеем: отдано в аккумулятор 2565мАч, получено из него 2480мАч. Соответственно, КПД аккумулятора составил примерно 97%. Ну а потери энергии на заряде/разряде — около 3%, т.е. для практических целей пренебрежимо малая величина. В общем, все в полном соответствии с теорией 🙂

Естественно, нужно делать какую-то скидку на точность измерения, на конкретный аккумулятор, внешние факторы (например, температуру аккумулятора или качество соединительных контактов, а также временной интервал между зарядом и разрядом), но в общем-то, это все уже «ловля блох», особого смысла не имеющая. Доказано главное: потери в литиевом аккумуляторе находятся где-то в районе 5%, а уж никак не 40%, как утверждал данный товарищ! 🙂

ЗЫ: На всякий случай уточняю: здесь речь идет о потерях только в самом аккумуляторе, без учета потерь в электронике (например, контроллер заряда)! Суммарные потери, естественно, всегда будут больше.

Также по теме:
Много букв об универсальных зарядниках 🙂
Универсальный зарядник B6S+ Mini

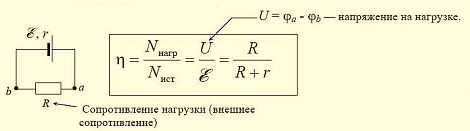
В процессе перемещения зарядов внутри замкнутой цепи, источником тока совершается определенная работа. Она может быть полезной и полной. В первом случае источник тока перемещает заряды во внешней цепи, совершая при этом работу, а во втором случае – заряды перемещаются во всей цепи. В этом процессе большое значение имеет КПД источника тока, определяемого, как соотношение внешнего и полного сопротивления цепи. При равенстве внутреннего сопротивления источника и внешнего сопротивления нагрузки, половина всей мощности будет потеряна в самом источнике, а другая половина выделится на нагрузке. В этом случае коэффициент полезного действия составит 0,5 или 50%.

КПД электрической цепи

Рассматриваемый коэффициент полезного действия в первую очередь связан с физическими величинами, характеризующими скорость преобразования или передачи электроэнергии. Среди них на первом месте находится мощность, измеряемая в ваттах. Для ее определения существует несколько формул: P = U x I = U2/R = I2 x R.

В электрических цепях может быть различное значение напряжения и величина заряда, соответственно и выполняемая работа тоже отличается в каждом случае. Очень часто возникает необходимость оценить, с какой скоростью передается или преобразуется электроэнергия. Эта скорость представляет собой электрическую мощность, соответствующую выполненной работе за определенную единицу времени. В виде формулы данный параметр будет выглядеть следующим образом: P=A/∆t. Следовательно, работа отображается как произведение мощности и времени: A=P∙∆t. В качестве единицы измерения работы используется джоуль (Дж).

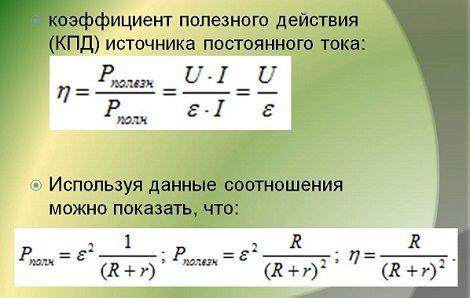
Для того чтобы определить, насколько эффективно какое-либо устройство, машина электрическая цепь или другая аналогичная система, в отношении мощности и работы используется КПД – коэффициент полезного действия. Данная величина определяется как отношение полезно израсходованной энергии, к общему количеству энергии, поступившей в систему. Обозначается КПД символом η, а математически определяется в виде формулы: η = A/Q x 100% = [Дж]/[Дж] х 100% = [%], в которой А – работа выполненная потребителем, Q – энергия, отданная источником. В соответствии с законом сохранения энергии, значение КПД всегда равно или ниже единицы. Это означает, что полезная работа не может превышать количество энергии, затраченной на ее совершение.

Таким образом, определяются потери мощности в какой-либо системе или устройстве, а также степень их полезности. Например, в проводниках потери мощности образуются, когда электрический ток частично превращается в тепловую энергию. Количество этих потерь зависит от сопротивления проводника, они не являются составной частью полезной работы.

Существует разница, выраженная формулой ∆Q=A-Q, наглядно отображающей потери мощности. Здесь очень хорошо просматривается зависимость между ростом потерь мощности и сопротивлением проводника. Наиболее ярким примером служит лампа накаливания, КПД у которой не превышает 15%. Остальные 85% мощности превращаются в тепловое, то есть в инфракрасное излучение.

Что такое КПД источника тока

Рассмотренный коэффициент полезного действия всей электрической цепи, позволяет лучше понять физическую суть КПД источника тока, формула которого также состоит из различных величин.

В процессе перемещения электрических зарядов по замкнутой электрической цепи, источником тока выполняется определенная работа, которая различается как полезная и полная. Во время совершения полезной работы, источника тока перемещает заряды во внешней цепи. При полной работе, заряды, под действием источника тока, перемещаются уже по всей цепи.

В виде формул они отображаются следующим образом:

• Полезная работа — Аполез = qU = IUt = I2Rt.
• Полная работа – Аполн = qε = Iεt = I2(R +r)t.

На основании этого, можно вывести формулы полезной и полной мощности источника тока:

• Полезная мощность – Рполез = Аполез /t = IU = I2R.
• Полная мощность – Рполн = Аполн/t = Iε = I2(R + r).

В результате, формула КПД источника тока приобретает следующий вид:

• η = Аполез/ Аполн = Рполез/ Рполн = U/ε = R/(R + r).

Максимальная полезная мощность достигается при определенном значении сопротивления внешней цепи, в зависимости от характеристик источника тока и нагрузки. Однако, следует обратить внимание на несовместимость максимальной полезной мощности и максимального коэффициента полезного действия.

Исследование мощности и КПД источника тока

Коэффициент полезного действия источника тока зависит от многих факторов, которые следует рассматривать в определенной последовательности.

Для определения величины тока в электрической цепи, в соответствии с законом Ома, существует следующее уравнение: i = E/(R + r), в котором Е является электродвижущей силой источника тока, а r – его внутренним сопротивлением. Это постоянные величины, которые не зависят от переменного сопротивления R. С их помощью можно определить полезную мощность, потребляемую электрической цепью:

• W1 = i x U = i2 x R. Здесь R является сопротивлением потребителя электроэнергии, i – ток в цепи, определяемый предыдущим уравнением.

Таким образом, значение мощности с использованием конечных переменных будет отображаться в следующем виде: W1 = (E2 x R)/(R + r).

Поскольку сила тока представляет собой промежуточную переменную, то в этом случае функция W1(R) может быть проанализирована на экстремум. С этой целью нужно определить значение R, при котором величина первой производной полезной мощности, связанная с переменным сопротивлением (R) будет равной нулю: dW1/dR = E2 x [(R + r)2 – 2 x R x (R + r)] = E2 x (Ri + r) x (R + r – 2 x R) = E2(r – R) = 0 (R + r)4 (R + r)4 (R + r)3

Из данной формулы можно сделать вывод, что значение производной может быть нулевым лишь при одном условии: сопротивление приемника электроэнергии (R) от источника тока должно достичь величины внутреннего сопротивления самого источника (R => r). В этих условиях значение коэффициента полезного действия η будет определяться как соотношение полезной и полной мощности источника тока – W1/W2. Поскольку в максимальной точке полезной мощности сопротивление потребителя энергии источника тока будет таким же, как и внутреннее сопротивление самого источника тока, в этом случае КПД составит 0,5 или 50%.

Задачи на мощность тока и КПД

Для школьников.

При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).

Превращение энергии из одного вида в другой всегда связано с работой.

Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:

Здесь

есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.

В гальваническом элементе сторонними силами являются силы химической реакции.

– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;

это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.

Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:

Здесь

есть полная или затраченная мощность, это мощность развиваемая источником тока.

это мощность выделяемая внутри источника тока

это полезная мощность, создаваемая во внешней части цепи (на нагрузке).

Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).

Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:

Ток в замкнутой цепи

тогда формулу для полезной мощности можно записать так:

Проанализируем зависимость полезной мощности от сопротивления нагрузки.

При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.

Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.

На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.

Получена формула для нахождения максимальной полезной мощности

При этом ток в цепи в два раза меньше тока короткого замыкания:

Но чему при этом будет равно КПД источника?

Из графика видно, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока КПД источника равен 50%.

Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:

Задачи (теория дана в предыдущей записи)

1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы.

Напряжение на зажимах аккумулятора:

Ток в цепи:

КПД аккумулятора:

Ответ: 1,43 В; 71 %.

2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи?

Максимальная полезная мощность:

Полезная мощность достигает максимального значения при

Ответ: 25 Вт; 1 Ом.

3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз?

Внутреннее сопротивление источника величина постоянная, его можно выразить из первого уравнения через R, затем найти второе значение КПД:

Ответ: 90%.

На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Зарядка и разрядка конденсатора.

Следующая запись: Занятие 59. Электрический ток в электролитах.

Ссылки на занятия до электростатики даны в Занятии 1.

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.

Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.

Что такое кпд аккумулятора

• ЖАНРЫ 362
• АВТОРЫ 289 602
• КНИГИ 698 649
• СЕРИИ 26 775
• ПОЛЬЗОВАТЕЛИ 612 783

Аккумуляторная батарея — одно из самых сложных устройств современного автомобиля. В ней непрерывно протекают многие электрохимические и физические процессы, взаимосвязанные и в значительной мере обусловленные влиянием внешних факторов. И как любое сложное устройство, требует соответствующего ухода при соответствующей квалификации.

Автолюбителя, в большинстве своем, интересуют чисто практические вопросы. Такие, как например, почему батарея уже через два сезона не обеспечивает пуск совершенно исправного двигателя? Почему батарея прослужила всего два года, а не 5 или 8 лет, хотя и прошел автомобиль по 3 тысячи км в год из-за отсутствия бензина? Что надо делать для того, чтобы аккумуляторная батарея служила долго и не подводила в самый неподходящий момент? И сколько ей уделять времени, и не следует ли с ней возиться каждый день? И многие другие подобные вопросы.

Для ответов на эти вопросы необходимо пользоваться не только готовыми рекомендациями и инструкциями, но и иметь определенный уровень знаний об аккумуляторных батареях.

Аккумуляторы, как и иные химические источники тока, интенсивно изучаются и совершенствуются, однако зачастую многие публикации недоступны для автолюбителя и понимание ряда вопросов требует специальной профессиональной подготовки. Во многих журнальных статьях, пособиях, рекомендациях, инструкциях и т.п. наряду с безусловно правильной и полезной информацией много субъективизма, а в ряде случаев, к сожалению, просматривается непонимание, незнание и корпоративные интересы авторов (особенно в журнале «За рулем»).

Настоящее пособие преследует очень простую цель — дать автолюбителю начальные знания по уходу за аккумуляторной батареей. Мы старались избежать сложных теоретических выкладок м формул. Тем не менее, полностью исключить теоретические сведения нельзя.

Без понимания основных процессов, протекающих в аккумуляторе в тех или иных условиях, невозможно построить оптимальную тактику ухода за аккумуляторной батареей в реальных условиях эксплуатации

(собственно аккумулятора), избежать досадных ошибок, даже пользуясь огромным количеством правильных рекомендаций.

Мы понимаем, что данное пособие тоже не лишено недостатков, однако постарались в логической последовательности изложить известные факты, различные методики и выполняемые работы по уходу за

аккумулятором. Надеемся, что материал, изложенный в пособии, поможет автолюбителю в уходе за аккумуляторной батареей.

2. ОСНОВНЫЕ ПРОЦЕССЫ В АККУМУЛЯТОРЕ

Аккумулятор является обратимым источником тока. Он способен отдавать в нагрузку во внешней цепи ранее запасенную энергию. На легковые автомобили устанавливаются аккумуляторные батареи, состоящие из шести последовательно включенных аккумуляторов. Они способны обеспечивать большие разрядные токи и относятся к классу стартерных аккумуляторных батарей. Это отражено в маркировке батарей. Например, батарея 6СТ-55 содержит 6 аккумуляторов, стартерная, номинальная энергоемкость составляет 55 ампер-часов.

Приведем некоторые основные понятия и определения, характеризующие аккумуляторную батарею в различных режимах работы.

Электродвижущая сила (ЭДС) — это разность электродных потенциалов при разомкнутой электрической цепи. ЭДС аккумулятора зависит от плотности температуры электролита и состава активной массы пластин. Выражается ЭДС в вольтах и обычно обозначается буквой Е. Измерить ЭДС можно вольтметром с большим внутренним сопротивлением, превышающим 20 кОм.

ЭДС покоя (Е0) — это ЭДС аккумулятора, находящегося длительное время (более 2-3 часов) без нагрузки.

ЭДС аккумулятора под нагрузкой отличается от ЭДС покоя. Это вызвано том, что при прохождении тока в цепи на электродах и в электролите происходят необратимые физические и химические процессы, связанные с потерей энергии. Один из них — это процесс поляризации.

ЭДС поляризации (Еп) — это ЭДС аккумулятора при наличии поляризации пластин.

Еп всегда направлена навстречу току.

При заряде ЭДС аккумулятора равна сумме ЭДС покоя и ЭДС поляризации:

Величину Е называют динамической ЭДС, или просто ЭДС аккумулятора.

В замкнутой электрической цепи постоянного тока, когда к аккумулятору подключены потребители, связи между ЭДС, проходящим по цепи током и сопротивлением цепи определяется по закону Ома:

I — сила тока в цепи, А;

R — активное сопротивление внешней цепи, Ом;

r — полное сопротивление участка электрической цепи внутри самого источника тока, Ом.

Выражение (1) можем переписать в виде:

т.е. ЭДС аккумулятора компенсирует падение напряжения на внешней цепи U=IR и падение напряжения внутри самого источника тока на его полном внутреннем сопротивлении Ur=I*r.

Величина U=I*R — это напряжение аккумулятора. Это напряжение на зажимах аккумулятора, которое используется для работы потребителей тока.

Из уравнения (2) видно, что при работе аккумулятора его напряжение U всегда меньше чем ЭДС, так как

По мере износа аккумулятора его внутреннее сопротивление возрастает. Это одна из причин пониженного напряжения на зажимах аккумулятора под нагрузкой. поскольку увеличивается Ur. У разряженного аккумулятора ситуация подобная.

Различают зарядное напряжение, равное

и разрядное напряжение:

где Iз — зарядный ток, А;

r — внутреннее сопротивление аккумулятора, Ом.

Нормальный зарядный ток — величина зарядного тока (А).

численно равная 0.1 емкости аккумуляторной батареи, выраженная в ампер-часах.

Внутреннее сопротивление аккумулятора складывается из сопротивления электродов, электролита и сопротивления, обусловленного сепараторами (прокладками между пластинами). Внутреннее сопротивление — величина непостоянная. Оно зависит от конструкции электродов, состояния активной массы, плотности электролита, температуры. В полностью заряженном аккумуляторе внутреннее сопротивление значительно меньше, чем у разряженного. Объясняется это тем, что электропроводность активной массы заряженного аккумулятора выше, чем у разряженного.

Емкость аккумулятора — это количество электричества, которое может запасти или отдать аккумулятор.

Емкость зависит от величины тока разряда. Емкость аккумулятора определяется как величина, равная произведению постоянного тока на время при 20-часовом режиме разряда до напряжения 1.7 В:

где Iр — величина разрядного тока,

tр — время разряда.

Емкость по току разрядная Qр — номинальная емкость аккумулятора при разряде:

где Ip — величина разрядного тока, А;

Зарядная емкость аккумулятора — характеризует количество электричества, полученное аккумулятором в процессе заряда:

где Qз — зарядная емкость, А*ч;

У современных аккумуляторов КПД по емкости равно 0.85.

Емкость по энергии — характеризует способность аккумулятора выполнить электрическую работу за определенное время.

Источник

Какой примерно КПД у литий ионных аккумуляторов?

Современные Li-ion аккумуляторы имеют высокие удельные характеристики: 100-180 Втч/кг и 250-400 Втч/л. Рабочее напряжение — 3,5-3,7 В.
Если еще несколько лет назад разработчики считали достижимой емкость Li-ion аккумуляторов не выше нескольких ампер-часов, то сейчас большинство причин, ограничивающих увеличение емкости, преодолено и многие производители стали выпускать аккумуляторы емкостью в сотни ампер-часов.
Современные малогабаритные аккумуляторы работоспособны при токах разряда до 2 С, мощные — до 10-20С. Интервал рабочих температур: от -20 до +60 °С. Однако многие производители уже разработали аккумуляторы, работоспособные при -40 °С. Возможно расширение температурного интервала в область более высоких температур.

Саморазряд Li-ion аккумуляторов составляет 4-6 % за первый месяц, затем — существенно меньше: за 12 месяцев аккумуляторы теряют 10-20% запасенной емкости. Потери емкости у Li-ion аккумуляторов в несколько раз меньше, чем у никель-кадмиевых аккумуляторов, как при 20 °С, так и при 40 °С. Ресурс-500-1000 циклов.

В формате AA их найти трудно. Но есть очень интересные образцы, например, Energizer L91 AA 1.5V Lithium Ultimate. Ёмкость 4.5Wh, держат высокие токи, срок хранения 15 лет, не боятся морозов до -40С. Вполне подойдут для заначки на случай ядерной войны или долгого похода по тайге/горам. В минусе: стоят дорого и очень трудно найти в продаже. Неперезаряжаемый литий в формате 123A найти проще.

Источник

Какой КПД у аккумулятора?

Тут недавно в комментах на ютьюбе прицепился ко мне немного странный товарищ, который пытался меня уверить, что ни в коем случае нельзя использовать «связку» солнечной батареи и буферного аккумулятора 🙂 Поскольку, по его версии, в аккумуляторе теряется 30-40% энергии — прямо вот ужас-ужас! Я-то, с младых ногтей, помню про совсем иную цифру для литиевых аккумуляторов: примерно 3-5% потерь, т.е. на порядок меньше 🙂

Но все же, малость «завел» он меня — так что я поставил небольшой эксперимент. Задача простая: нужно померить КПД аккумулятора, или иными словами, посчитать разницу между энергией, израсходованной на зарядку аккумулятора и той энергией, которую мы можем потом из этого аккумулятора получить обратно.

Проще всего подобный замер было сделать с помощью универсального зарядника iMax, поскольку он умеет как заряжать, так и разряжать аккумуляторы, и при этом еще показывает, сколько в аккумулятор ушло, и сколько мы от него получили.

В общем, я взял аккумулятор, разрядил его (iMax разряжает до напряжения 3В, что меня для целей данного эксперимента вполне устраивает), потом полностью зарядил и снова разрядил. Результаты представлены на фото.

В сухом остатке имеем: отдано в аккумулятор 2565мАч, получено из него 2480мАч. Соответственно, КПД аккумулятора составил примерно 97%. Ну а потери энергии на заряде/разряде — около 3%, т.е. для практических целей пренебрежимо малая величина. В общем, все в полном соответствии с теорией 🙂

Естественно, нужно делать какую-то скидку на точность измерения, на конкретный аккумулятор, внешние факторы (например, температуру аккумулятора или качество соединительных контактов, а также временной интервал между зарядом и разрядом), но в общем-то, это все уже «ловля блох», особого смысла не имеющая. Доказано главное: потери в литиевом аккумуляторе находятся где-то в районе 5%, а уж никак не 40%, как утверждал данный товарищ! 🙂

ЗЫ: На всякий случай уточняю: здесь речь идет о потерях только в самом аккумуляторе, без учета потерь в электронике (например, контроллер заряда)! Суммарные потери, естественно, всегда будут больше.

Источник

КПД повербанков и схем заряда гаджетов

Power Bank (внешний аккумулятор, портативное зарядное устройство, повербанк) — коробочка с аккумуляторами и электроникой внутри, позволяющая заряжать гаджеты там, где нет розеток.

Производители повербанков никогда не указывают реальное количество энергии, которое может выдать power bank. Всегда указывается лишь ёмкость внутренних аккумуляторов в миллиампер-часах. Многие наивно думают, что повербанк, на котором написано 10000 mAh может зарядить смартфон с аккумулятором 2500 mAh четыре раза. На самом деле это совсем не так.

Я измерил количество энергии, которые смогли выдать пять разных повербанков и количество энергии, которое потребовалось пяти разным смартфонам и планшетам, чтобы полностью зарядить аккумулятор.

Повербанки разряжались током 950 mA.

Модель	mAh	Wh аккумулятора	Wh на выходе	КПД
Miller ML-102 V7.1	2580	9,55	8,46	88,6%
Huawei AP006	4800	17,80	16,79	94,3%
Just Mobile PP-268	6000	22,20	17,47	78,7%
Gigabyte OTG G66B1	6600	24,42	21,69	88,8%
Xiaomi NDY-02-AD	10400	37,44	34,58	92,4%

По результатам измерений КПД повербанков составил от 78.7 до 94.3%.

Необходимо заметить, что у меня была возможность измерить ёмкость внутреннего аккумулятора только в случае с Miller, в остальных четырёх случаях остаётся лишь верить (или не верить) производителю. Могу предположить, что ёмкость аккумулятора в Just Mobile реально меньше, чем заявленные 6000 mAh.

Ещё замечу, что у Xiaomi на корпусе указана ёмкость аккумулятора 37,44Wh, рассчитанная исходя из номинального напряжения 3.6V (обычно ёмкость рассчитывается исходя из напряжения 3.7V).

Теперь посмотрим, сколько энергии требуется смартфонам и планшетам, чтобы полностью зарядить аккумулятор. Перед экспериментом аккумулятор устройства полностью разряжался, затем подключалась зарядка, а через минуту включалось устройство.

Модель	mAh	Wh аккумулятора	Wh на входе	Превышение
ASUS Zenfone 5	2110	7,81	10,73	37,4%
HTC Desire Eye	2400	8,88	12,71	43,1%
Huawei Ascend P7	2500	9,25	12,57	35,9%
Samsung Galaxy Note 8.0	4600	17,02	23,54	38,3%
Apple iPad Air	32,40	41,87	29,2%

Устройствам для зарядки требуется на 29.2-43.1% больше энергии, чем энергия их аккумулятора. Для большинства устройств это превышение составляет 37-38% и только iPad имеет более совершенную схему зарядки с высоким КПД, дающую превышение 29.2%.

Таким образом, если заряжать самый неэкономный в плане зарядки смартфон HTC Desire Eye (аккумулятор 2400 mAh) от повербанка Just Mobile PP-268 (аккумулятор 6000 mAh), имеющего самый низкий КПД из протестированных, повербанка хватит лишь на 1.3 полных зарядки, а совсем не на 2.5 зарядки (6000/2400).

В среднем можно считать, что КПД всей электроники при зарядке смартфона или планшета от повербанка составляет около 65%.

Поэтому при приблизительных рассчётах, сколько раз тот или иной гаджет получится зарядить от повербанка, нужно ёмкость аккумуляторов гаджета умножить на 1.5 и разделить ёмкость аккумуляторов повербанка на получившееся число.

Пример: В смартфоне стоит аккумулятор 2000 mAh, в повербанке — 6000mAh. 6000/(2000×1.5)=2. Повербанка хватит ровно на две зарядки.

Источник