Как найти кпд цикла происходят

На этой странице вы узнаете

• В чем прелесть фазовых переходов?
• Что лучше выбрать: Mercedes или BMW?

Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов,а именно получать тепловую энергию различными доступными способами. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне. 

Тепловые машины и их КПД

Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.

Мы не почувствуем, как испарится капелька у нас на руке, потому что это не требует много тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. А зачем мы вообще рассматриваем эти фазовые переходы? Все дело в том, что именно фазовые переходы являются ключевым звеном во всех процессах, где нас просят посчитать КПД, от них нашему рабочему телу и подводится теплота нагревателя.

Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.

Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую. 

Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в автомобилях часть энергии от сгоревшего бензина идет на движение. Схематично можно изобразить так:

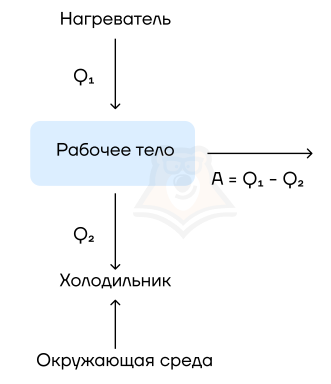
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q₁, из которой A уходит на работу механизма. Остаток теплоты Q₂ рабочее тело отдает холодильнику, по сути — это потеря энергии.

Физика не была бы такой загадочной, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:

Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.

Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери. 

Полезную работу можно расписать как Q₁ — Q₂ (по закону сохранения энергии). Тогда формула примет вид:

(eta = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})

Цикл Карно

Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже все сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат. Рассмотрим, как этот цикл выглядит в координатах p(V).

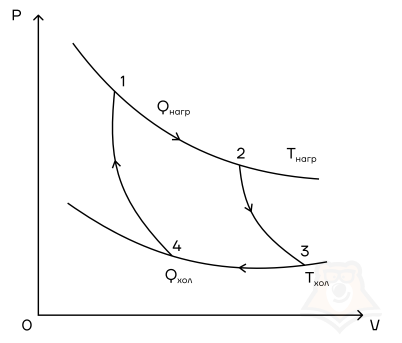
• Температура верхней изотермы 1-2 — температура нагревателя (так как теплота в данном процессе подводится).
• Температура нижней изотермы 3-4 — температура холодильника (так как теплота в данном процессе отводится).
• 2-3 и 4-1 — это адиабатические расширение и сжатие соответственно, в них газ не обменивается теплом с окружающей средой.

Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД. 

Формула, по которой можно рассчитать ее КПД выражается через температуры:

Приступим к задачам

Задачи на данную тему достаточно часто встречаются в задании 27 из КИМа ЕГЭ. Давайте разберем некоторые примеры.

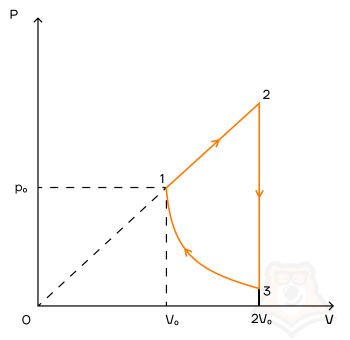
Задание 1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A₁₂ = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Q_хол| = 4780 Дж. Найдите работу газа |A₁₃| на адиабате, если количество вещества постоянно.

Решение:

Шаг 1. Первое, с чего лучше начинать задачи по термодинамике — исследование процессов. 

Посмотрим на участок 1-2 графика: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: (frac{pV}{T} = const). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем.  Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.

Участок 2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: (frac{p}{T} = const). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.

Участок 3-1: адиабата по условию, то есть количество теплоты в этом переходе равна нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем. 

Оформим все данные в таблицу. 

Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.

Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.

Шаг 2. Первый закон термодинамики для процесса 1-2 запишется в виде: 

Q₁₂ = ΔU₁₂ + A₁₂. 

Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции: 

(A_{12} = frac{p_0 + 2p_0}{2} * V0 =frac{3p_0V_0}{2}). 

Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:

(Delta U_{12} = frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = frac{9p_0V_0}{2}). 

Заметим, что это в 3 раза больше работы газа на этом участке: 

(Delta U_{12} = 3A_{12} rightarrow Q_{12} = 4A_{12}).

Шаг 3. Работа цикла — площадь фигуры, которую замыкает график, тогда . A = A₁₂ — |A₃₁|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q₁₂ — |Q₃₁|.

 Сравним эти формулы:

Q₁₂ -|Q₃₁| = A₁₂ — |A₃₁|,

подставим выражения из предыдущего пункта:

4A₁₂ — |Q₃₁| = A₁₂ — |A₃₁| (rightarrow) |A₃₁| = -3A₁₂ + |Q₃₁| = -31520 + 4780 = 220 Дж.

Ответ: 220 Дж

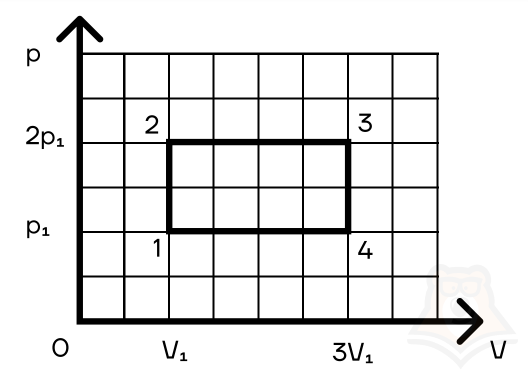
Задание 2. Найти КПД цикла для идеального одноатомного газа.

Решение:

Шаг 1. КПД цикла определим по формуле: (eta = frac{A}{Q}), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p₁ — p₁)(3V₁ — V₁) = 2p₁V₁.

Шаг 2. Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:

Посмотрим на участок 1-2 графика: давление растет, объем не меняется. По закону Шарля (frac{p}{T} = const) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.

2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака (frac{V}{T} = const) температура тоже растет, растет и внутренняя энергия.

3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.

4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.

Оформим данные в таблицу: 

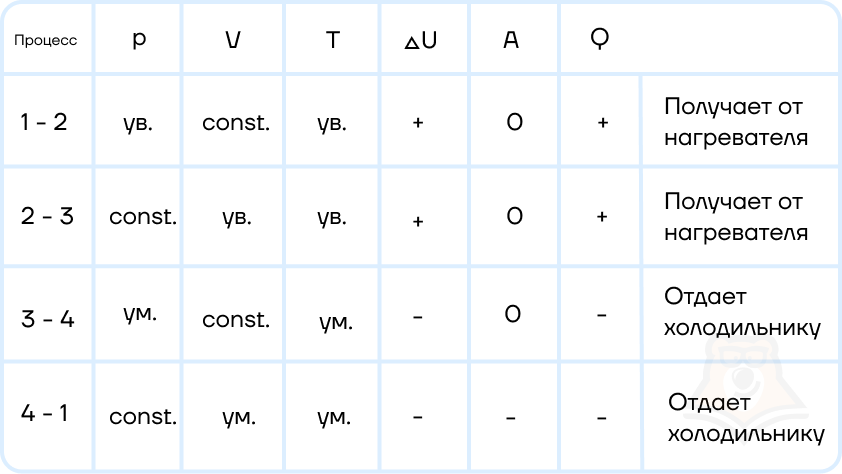
Отметим, что  необходимое Q = Q₁₂ + Q₂₃.

Шаг 3. Запишем первый закон термодинамики для процессов 1-2 и 2-3:

(Q_{12} = U_{12} + A_{12} = Delta U_{12} = frac{3}{2}(2p_1V_1 -p_1V_1) = frac{3}{2}p_1V_1).
(Q_{23} = Delta U_{23} + A_{23}), работу газа найдем как площадь под графиком: A₂₃ = 2p₁(3V₁ — V₁) = 4p₁V₁.
(Delta U_{12} = frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1).
(Q_{23} = Delta U_{23} + A_{23} = 10p_1V_1).

Шаг 4. Мы готовы считать КПД: (eta = frac{A}{Q} = frac{A}{Q_{12} + Q_{23}} = frac{2p_1V_1}{frac{3}{2}p_1V_1 + 10p_1V_1} = frac{4}{23} approx 0,17).

Ответ: 17%

Теперь вас не должно настораживать наличие графиков в условиях задач на расчет КПД тепловых машин. Продолжить обучение решению задач экзамена вы можете в статьях «Применение законов Ньютона» и «Движение точки по окружности».

Фактчек

• Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую. 
• Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
• Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
  (eta = frac{A}{Q_1} = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})  
• Цикл Карно — цикл с максимально возможным КПД: (eta = frac{T_1 — T_2}{T_1} = 1 — frac{T_2}{T_1})
• Не забываем, что работа считается, как площадь фигуры под графиком.

Проверь себя

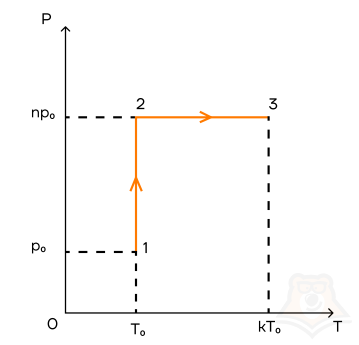
Задание 1. 
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T₀ = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.

1. 5672 Дж
2. 4731 Дж
3. 5817 Дж
4. 6393 Дж

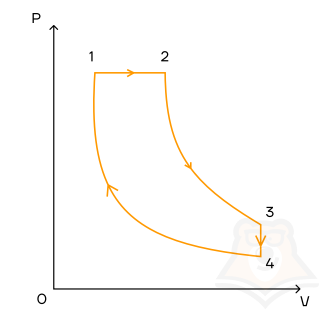
Задание 2. 
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT₁₂ к изменению его температуры ΔT₃₄ при изохорном процессе равен 1,5. Определите КПД цикла.

1. 0,6
2. 0,5
3. 0,8
4. 1

Задание 3.
В топке паровой машины сгорело 50 кг каменного угля, удельная теплота сгорания которого равна 30 МДж/кг. При этом машиной была совершена полезная механическая работа 135 МДж. Чему равен КПД этой тепловой машины? Ответ дайте в процентах.

1. 6%
2. 100%
3. 22%
4. 9%

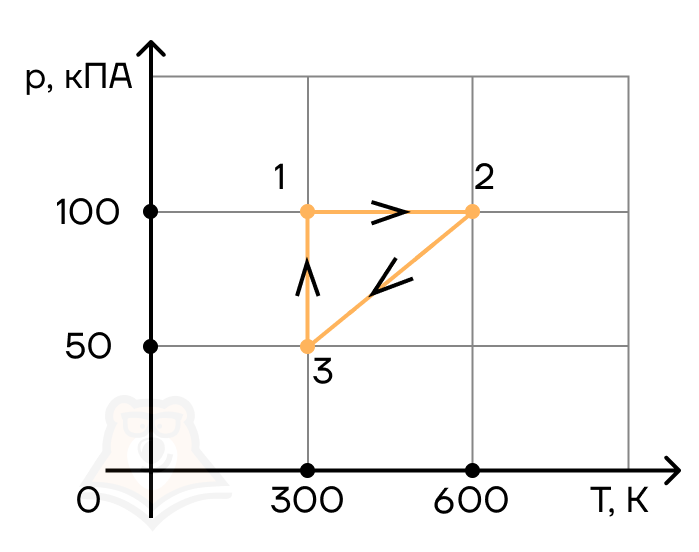
Задание 4.
С двумя молями одноатомного идеального газа совершают циклический процесс 1–2–3–1 (см. рис.). Чему равна работа, совершаемая газом на участке 1–2 в этом циклическом процессе?

1. 4444 Дж
2. 2891 Дж
3. 4986 Дж
4. 9355 Дж

Ответы:1 — 3; 2 — 1; 3 — 4; 4 — 3.

Полное условие задачи

Найдите КПД цикла, изображенного на рисунке для идеального одноатомного газа.

Краткое условие задачи

Решение задачи

КПД цикла находим по формуле:

где работа определяется как площадь прямоугольника 1234:

Для определения затраченного количества теплоты нужно выяснить, в каких процессах газ получал теплоту. Для этого воспользуемся первым законом термодинамики, формулой для изменения внутренней энергии и уравнением состояния идеального газа:

Рассмотрим каждый процесс по отдельности.

В процессе 1 – 2 начальная температура меньше конечной:

поэтому изменение внутренней энергии больше нуля:

а работа равна нулю, поскольку процесс изохорный:

Отсюда следует, что газ в процессе 1 – 2 получал тепло:

Найдем это тепло:

Разность температур найдем используя уравнение состояния идеального газа. Запишем его для состояния 1 и для состояния 2:

Вычитаем из второго уравнения первое и находим разность температур:

Подставим в формулу для теплоты:

В процессе 2 – 3 начальная температура также меньше конечной:

поэтому изменение внутренней энергии также больше нуля:

а работа в этом процессе больше нуля (газ совершает работу):

поскольку объем увеличивается:

Отсюда следует, что газ в процессе 2 – 3 тоже получал тепло:

Найдем это тепло:

Разность температур найдем используя уравнение состояния идеального газа. Запишем его для состояния 2 и для состояния 3:

Вычитаем из второго уравнения первое и находим разность температур:

Подставим в формулу для теплоты:

В процессе 3 – 4 начальная температура больше конечной:

поэтому изменение внутренней энергии меньше нуля:

а работа равна нулю, поскольку процесс изохорный:

Отсюда следует, что газ в процессе 3 – 4 отдает тепло:

В процессе 4 – 1 начальная температура также больше конечной:

поэтому изменение внутренней энергии также меньше нуля:

работа в этом процессе тоже меньше нуля (над газом совершают работу):

поскольку объем уменьшается:

Отсюда следует, что газ в процессе 4 – 1 тоже отдает тепло:

Таким образом затраченная теплота равна:

Искомый КПД равен:

Или

Ответ: 17 %.

Речь в статье пойдет о КПД различных циклов, проводимых с газом. При этом давайте помнить, что внутренняя энергия изменяется тогда, когда изменяется температура, а в адиабатном процессе передачи тепла не происходит, то есть для совершения работы в таком процессе газ “изыскивает внутренние резервы”. Кроме того, работа численно равна площади под кривой процесса, а работа за цикл – площади внутри цикла.

Задача 1.

На рисунке представлена диаграмма цикла с одноатомным идеальным газом. Участки и – адиабаты.  Вычислите КПД данной тепловой машины и максимально возможный КПД .

КПД тепловой машины можно вычислить как

Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:

Работа численно равна площади, ограниченной циклом. Поэтому

Участк и по условию – адиабаты, то есть передачи тепла газу на этих участках не происходит, следовательно, работа будет совершена за счет «внутренних резервов» – то есть внутренней энергии. Нужно, следовательно, найти, как она изменилась.

Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и , и , это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать . Но, так как , а ,то изменение внутренней энергии будет равно

Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке :

Ответ: , .

Задача 2.

Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж.  В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу кДж. Найдите КПД данной тепловой машины.

Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.

Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД

Ответ: .

Задача 3.

КПД  тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе кДж. Найдите разность максимальной и минимальной  температур  газа в цикле.

Полная площадь под кривой процесса 1-2 равна кДж. При этом, так как КПД машины 25%, то площадь внутри цикла равна , а под кривой 3-1  – .  В процессе 1-2 изменения внутренней энергии не было, так как температура не менялась, а в процессе 3-1 газу не передавали тепло, следовательно, работа совершена за счет внутренней энергии. Т.е.

Ответ: 500 K.

Термодинамические циклы
Эдвардса Аткинсона Брайтона/Джоуля Гирна Дизеля Калины Карно Ленуара Миллера Отто Ренкина Стирлинга Тринклера Хамфри Эрикссона
Статья является частью серии «Термодинамика»

В термодинамике цикл Карно́ или процесс Карно́ — это идеальный^[1] круговой процесс, состоящий из двух адиабатных и двух изотермических процессов^[2]. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником^[3].

Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году^[4][5].

Поскольку идеальные процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному процессу Карно только с большей или меньшей степенью точности.

Коэффициент полезного действия (КПД) любой тепловой машины не может превосходить КПД идеальной тепловой машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника^[6]. По этой причине, позволяя оценить верхний предел КПД тепловой машины, цикл Карно важен для теории тепловых машин. В то же время КПД цикла Карно настолько чувствителен к отклонениям от идеальности (потерям на трение), что данный цикл никогда не применяли в реальных тепловых машинах^{[K 1][8]}.

Описание цикла Карно[править | править код]

Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температурой и рабочего тела.

Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах (температура) и (энтропия).

1. Изотермическое расширение (на рис. 1 — процесс A→B). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счет передачи от нагревателя количества теплоты , то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.

2. Адиабатическое расширение (на рис. 1 — процесс B→C). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника , тело совершает механическую работу, а энтропия остаётся постоянной.

3. Изотермическое сжатие (на рис. 1 — процесс C→D). Рабочее тело, имеющее температуру , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты . Над телом совершается работа, его энтропия уменьшается.

4. Адиабатическое сжатие (на рис. 1 — процесс D→A). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.

Обратный цикл Карно[править | править код]

В термодинамике холодильных установок и тепловых насосов рассматривают обратный цикл Карно, состоящий из следующих стадий^[9][10]: адиабатического сжатия за счёт совершения работы (на рис. 1 — процесс C→B); изотермического сжатия с передачей теплоты более нагретому тепловому резервуару (на рис. 1 — процесс B→A); адиабатического расширения (на рис. 1 — процесс A→D); изотермического расширения с отводом теплоты от более холодного теплового резервуара (на рис. 1 — процесс D→C).

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику

Отсюда коэффициент полезного действия тепловой машины Карно равен

Первая и вторая теоремы Карно[править | править код]

Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно^[11]. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно^[12][13]. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.

Связь между обратимостью цикла и КПД[править | править код]

Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.

Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД^[14]. Возможны и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например цикл Эрикссона  (англ.) (рус., состоящий из двух изобар и двух изотерм^[14].

Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.

См. также[править | править код]

• Термодинамические циклы
• Первое начало термодинамики
• Второе начало термодинамики
• Термодинамическая энтропия
• Термодинамические потенциалы

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

• Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. — Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. — 102 p. (фр.)
• Бахшиева Л. Т., Кондауров Б. П., Захарова А. А., Салтыкова В. С. Техническая термодинамика и теплотехника / Под ред. проф А. А. Захаровой. — 2-е изд., испр. — М.: Академия, 2008. — 272 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-4999-1.
• Бэр Г. Д. [download1.libgen.io/ads.php?md5=F54DE2B5B715C97EA3375A180801C390 Техническая термодинамика]. — М.: Мир, 1977. — 519 с. (недоступная ссылка)
• Кинан Дж. Термодинамика / Пер с англ. А. Ф. Котина под ред. М. П. Вукаловича. — М.—Л.: Госэнергоиздат, 1963. — 280 с.
• Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V).
• Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. — 2-е изд., испр. и доп. — М.: Металлургия, 1973. — 256 с.
• Николаев Г. П., Лойко А. Э. Техническая термодинамика. — Екатеринбург: УрФУ, 2013. — 227 с.
• Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. — 2-е изд., испр. и доп. — Новосибирск: Изд-во Носиб. ун-та, 2000. — 608 с. — ISBN 5-7615-0383-2.
• Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
• Кудрявцев П. С. История физики. — М.: Гос. учебно-педагог. изд-во, 1956. — Т. 1. От античной физики до Менделеева. — 564 с. — 25 000 экз.
• Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — 5 изд., испр.. — М.: ФИЗМАТЛИТ, 2005. — 544 с. — ISBN 5-9221-0601-5.

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок download1.libgen.io/ads.php?md5=F54DE2B5B715C97EA3375A180801C390

2014-05-31   

Найдите КПД цикла, приведенного на диаграмме $p, V$ на (рис. а). Рабочим телом служит один моль идеального одноатомного газа.

Решение:

КПД цикла определяется отношением работы А, совершаемой газом за время цикла, к количеству теплоты $Q_{н}$, подведенному к газу от нагревателя за это время:

$eta = A/Q_{н}$. (1)

Работа А численно равна площади изображенного на (рис. б) треугольника ABC:

$A=frac{1}{2}p_{0}V_{0}$. (2)

Чтобы найти $Q_{н}$, рассмотрим превращения энергии, происходящие на участках АВ, ВС и СА замкнутого цикла ABCА. Используем уравнение состояния газа $pV=RT$, находим температуры газа $T_{1},T_{B}$ и $T_{C}$ в состояниях, отвечающих точкам А, В и С цикла:

$T_{A}=p_{0}V_{0}/R, T_{B}=T_{C}=2p_{0}V_{0}/R$.

На участке АВ идет изохорический процесс. Газ работы не совершает, а его внутренняя энергия изменяется на величину

$Delta U_{AB}= frac{3}{2}R(T_{B}-T_{A}) = frac{3}{2}p_{0}V_{0}/R$.

Согласно первому началу термодинамики это увеличение внутренней энергии газа происходит за счет подвода некоторого количества теплоты

$Q_{AB} = Delta U_{AB} = frac{3}{2} p_{0}V_{0} > 0$.

На участке СА идет изобарический процесс. Газ сжимается и совершает отрицательную работу

$A_{CA}=p_{0} Delta V = – p_{0}V_{0}$,

а его внутренняя энергия изменяется на величину

$Delta U_{CA}=frac{3}{2}p_{0}V_{0}<0$.

Таким образом, на участке СА имеет место неравенство $A_{CA}<0$ и $U_{CA} < 0$ и, следовательно, газ отдает тепло $(Q_{CA} < 0)$.

Выясним теперь, что происходит на участке ВО, который представляет собой часть участка ВС. Точка О (см. рис. б) текущая точка участка ВС. Обозначим параметры газа (давление, объем и температуру), отвечающие точке О, буквами $p,V$ и $T$, они

показаны уравнением состояния. На участке ВО внутренняя энергия газа изменяется на величину

$Delta U_{BO}= frac{3}{2}R(T-T_{B})=frac{3}{2}(pV-2p_{0}V_{0})$.

При этом газ совершает работу $A_{BO}$, численно равную площади заштрихованной на рис., трапеции:

$A_{BO}=(p_{0}+p/2)(V-V_{0})$.

Согласно первому началу термодинамики на изменение внутренней энергии газа $Delta U_{BO}$ и совершение работы $A_{BO}$ системе должно быть передано количество теплоты

$Q_{BO}= Delta U_{BO} +A_{BO} = frac{3}{2}(pV-2p_{0}V_{0})+ left ( p_{0} +frac{p}{2} right ) (V-V_{0})$. (3)

Hа участке ВС (в который входит и участок ВО) объем газа V и это давление р, как следует из графика, приведенного на рис. б, показаны следующей зависимостью:

$p=p_{0}(3-v/V_{0})$. (4)

Подставляя в (3) выражение для р (4), имеем

$Q_{BO}=-frac{p_{0}}{2} left ( 4frac{V^{2}}{V_{0}} – 15V +11 V_{0} right )$. (5)

Из (5) следует, что зависимость $Q_{BO}$ от $V$ представляется параболой, пересекающей ось $V$ в точках с координатами

$V_{1}=V_{0}$ и $V_{2}=frac{11}{4}V_{0} = 2,75 V_{0}$.

Вершине параболы отвечает значение

$V=V_{0} equiv frac{V_{1}+V_{2}}{2} = frac{15}{8}V_{0}$

Но время процесса ВО при изменении V от значения $V_{0}$ до значения $V_{D}$ количество теплоты, переданное газу, монотонно растет, и к моменту, когда точка О совмещается с точкой D, оно составляет

$Q_{BD} = Q_{BO}(V) |_{V=V_{D}}=frac{49}{32} p_{0}V_{0}$.

Когда точка О находится в пределах участка DC и приближается к точке С, величина $Q_{BO}$ монотонно уменьшается. Это означит, что на участке DC газ отдает тепло.

Итак, система получает тепло от нагревателя только на участке АВ и BD:

$Q_{н}=Q_{AB} +Q_{BD} = frac{97}{32} p_{0}V_{0}$. (6)

Из (1), (2) и (6) находим: $ eta = frac{16}{97} approx 16,5%$.