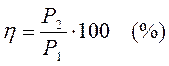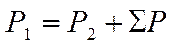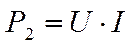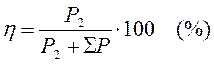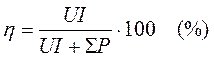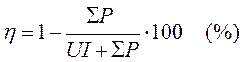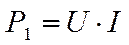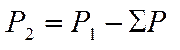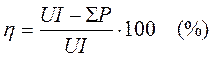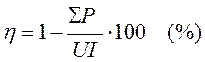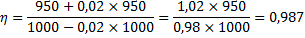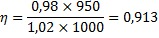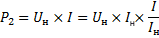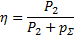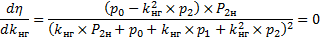Как найти кпд генератора постоянного тока

In this article, we have listed all the important formulas and equations related to DC
generators used in different electrical practices like design, simplify, and analysis. This page
can serve as a DC generator formula handbook for electrical engineering students and
professionals.

DC Generator Definition

An electromechanical energy conversion machine that converts rotational mechanical energy
into DC electrical energy is referred to as a DC generator. A DC generator consists of two
parts namely stator and rotor. The stator forms the field system of the machine, while the
rotor acts as the armature.

Types of DC Generator

Based on armature and field winding connections, generators are classified into the following
three types −

• Series DC Generator − The field winding is connected in series with the armature winding.

• Shunt DC Generator − The field winding is connected in parallel with the armature winding.

• Compound DC Generator − It has both series and shunt field windings connected with the armature winding.

Main Parts of a DC Generator

A typical DC generator consists of three-main parts namely – magnetic field system,
armature, and commutator and brushgear.

EMF Equation of DC Generator

The mathematical expression which helps to determine the induced or generated EMF of the
DC generator is known as the EMF equation of the DC generator. It is given by,

$$mathrm{E_{g}=frac{NPphi Z}{60A}}$$

Where, N is the speed of armature in RPM, P is the number of poles in the machine, ϕ is the
magnetic flux per pole, Z is the number of armature conductors, and A is the number of
parallel paths in armature winding.

The emf equation for wave wound DC generator (A = 2) is given by,

$$mathrm{E_{g}=frac{NPphi Z}{120}}$$

The EMF equation for lap wound DC generator (A = P) is given by,

$$mathrm{E_{g}=frac{Nphi Z}{60}}$$

Generated Power and Load Power of DC Generator

The power developed in the armature of a DC generator is called generated power. The
generated power by a DC generator is given by,

$$mathrm{P_{g}=E_{g}I_{a}}$$

The amount of power that is supplied to the load by a DC generator is called load power. The
load power of a DC generator is given by,

$$mathrm{P_{L}=V_{T}I_{L}}$$

Where, V_T is the terminal voltage, and IL is the load current.

Terminal Voltage of DC Generator

The part of total emf induced available at the load terminals of a DC generator is known as
the terminal voltage of the DC generator.

Terminal Voltage of Series DC Generator

For a series DC generator, the terminal voltage is given by,

$$mathrm{V_{T}=E_{g}-I_{a}left ( R_{a}+R_{se} right )}$$

Where, E_g is the total generated emf, I_a is the armature current, R_a is the armature winding
resistance, and R_se is the series field resistance.

Terminal Voltage of Shunt DC Generator

For a shunt DC generator, the terminal voltage is given by,

$$mathrm{V_{T}=E_{g}-I_{a}R_{a}}$$

Armature Current of DC Generator

The total current that flows through the armature winding when a load is connected to a DC
generator is known as the armature current of a DC generator.

Armature Current of Series DC Generator

The armature current of a series DC generator is given by,

$$mathrm{I_{a}=I_{se}=frac{E_{g}-V_{T}}{R_{a}+R_{se}}}$$

Armature Current of Shunt DC Generator

The armature current of a shunt DC generator is given by,

$$mathrm{I_{a}=I_{sh}+I_{L}}$$

Where, I_sh is the shunt field current, and I_L is the load current.

Field Current of Shunt DC Generator

In the shunt DC generator, the electric current that flows through the shunt field winding to
produce the working magnetic flux is known as its field current.

$$mathrm{I_{sh}=frac{V_{T}}{R_{sh}}}$$

Where, R_sh is the resistance of shunt field winding.

Total Output Power of DC Generator

The amount of electrical power that is delivered to the load by the DC generator is known as
the total output power of the DC generator.

The output power of a DC generator is given by,

$$mathrm{P_{out} = P_{in} – (core: losses + copper: losses + mechanical: losses + stray: losses)}$$

Where, P_in is the total input mechanical power, and P_out is the total output electrical power.

DC Generator Losses

The amount of generated power which is wasted in the form of heat and does not delivered to
the load is called power loss. In a DC generator, the total power loss is given by,

$$mathrm{Losses = P_{cu}+P_{i}+P_{m}+P_{stray}}$$

Where, P_cu is the copper loss in armature and field windings, P_i is the iron losses in iron cores
of generator, Pm is the mechanical loss (friction and windage losses), and P_stray is the stray
loss such as power loss in metal body due to induction.

Efficiency of DC Generator

The ratio of the output power to the input power to a DC generator is known as efficiency of
the DC generator.

$$mathrm{Efficiency,eta = frac{Output: power}{Input: power}}$$

For a DC generator, we have defined three efficiencies namely, mechanical efficiency,
electrical efficiency, and overall efficiency.

Mechanical Efficiency of DC Generator

The ratio of mechanical power in the armature to the total input mechanical power is referred
to as the mechanical efficiency of the DC generator. It is given by,

$$mathrm{eta_{mech} = frac{Mechanical: power: developed : in: armature}{Input:mechanical: power}}$$

$$mathrm{Rightarrow eta_{mech} = frac{E_{g}I_{a}}{omega tau }}$$

Where, ωτ is the mechanical power input through the shaft.

Electrical Efficiency of DC Generator

The ratio of output electrical power to the armature power is known as electrical efficiency of
the DC generator.

$$mathrm{eta_{elect} = frac{Output: electrical: powerleft ( V_{T}I_{L} right )}{Armature: powerleft ( E_{g}I_{a} right ) }}$$

Overall Efficiency of DC Generator

The ratio of output electrical power to the input mechanical power is known as the overall
efficiency of the dc generator.

$$mathrm{eta_{overall} = frac{Output: electrical: powerleft ( V_{T}I_{L} right )}{Input: mechanical: powerleft (omega tau right) }}$$

$$mathrm{Rightarrow eta_{overall} = frac{V_{T}I_{L}}{V_{T}I_{L}+Losses }}$$

Condition for Maximum Efficiency of DC Generator

For the maximum efficiency of a DC generator, the variable losses (copper losses in field and
armature windings) and the constant losses (core losses and mechanical losses) must be
equal, i.e.,

$$mathrm{Variable: losses = Constant: losses}$$

Conclusion

In this article, we listed all the important formulae of DC generators used for design and
analysis of the DC generator. All these formulae are very important for electrical engineering
students and practicing electrical professionals.

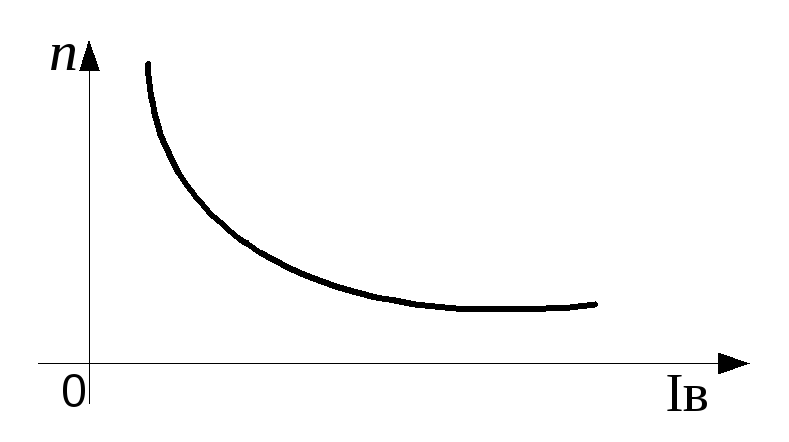
О свойствах
генератора судят по характеристикам,
показывающим зависимость между основными
величинами, определяющими работу машины.
Основные характеристики генератора:
холостого хода, внешняя, регулировочная.

Характеристика
холостого хода – это зависимость ЭДС
якоря от тока возбуждения при токе
нагрузки
и его частоте вращения(рис.1.4). При этом ЭДСпропорциональна магнитному потоку.

Благодаря
остаточному магнитному полю при
и характеристика не проходит через
начало координат.

Характеристика
состоит из трех частей: начальная
прямолинейная часть, где магнитная
система не насыщена, и при увеличении
тока возбуждения магнитный

поток
и ЭДС увеличиваются (участок);
“колено” характеристики, где магнитная
система находится в полунасыщенном
состоянии и рост магнитного потока и
ЭДС замедляются (участок 1 – 2); магнитная
система насыщена (участок 2 – 3).

Рис. 1.4

Положение точки
А, соответствующее номинальной ЭДС,
дает возможность судить об устойчивости
напряжения генератора при работе и о
пределах, в которых можно регулировать
напряжение.

Если бы точка
А находилась на прямолинейной части
характеристики, то незначительные
изменения
,
вызывали бы значительные изменения ЭДС
и напряжения. В этом случае работа
генератора была бы неустойчивой.

Если точка А
находится на участке 2 – 3, то колебания
напряжения незначительны, и генератор
работает устойчиво, но возможность
регулирования напряжения невелика, так
как магнитная система машины насыщена.
Поэтому точка А, соответствующая
номинальной ЭДС, расположена на “колене”
характеристики холостого хода.

Генераторы
независимого и параллельного возбуждения
имеют аналогичные характеристики
холостого хода.

Внешняя характеристика
– это зависимость напряжения на зажимах
генератора от тока нагрузки
при;.

Уравнение
электрического состояния цепи якоря

,
(2)

где

– внутреннее сопротивление цепи якоря,
состоящее из сопротивления обмотки
якоря, обмотки дополнительных полюсов,
сопротивления щеток и коллектора;

–для
генератора независимого возбуждения;

–для
генератора параллельного возбуждения;

–ток
нагрузки.

Как
видно из уравнения (2), напряжение на
зажимах генератора независимого
возбуждения при увеличении тока нагрузки
уменьшается по двум причинам:

1.
Увеличение падения напряжения

в цепи якоря.

2.
Возрастающее влияние потока якоря на
основной поток полюсов (размагничивающее
действие реакции якоря), приводящее к
уменьшению ЭДС
.

Внешняя
характеристика генератора независимого
возбуждения имеет вид кривой 1 (рис.5).

В генераторах
параллельного возбуждения к двум
указанным причинам добавляется третья
– уменьшение тока возбуждения
вследствие понижения напряжения,
вызванного первой и второй причинами.
Уменьшение тока возбуждения вызывает
уменьшение магнитного потока, ЭДС ()
и дополнительное уменьшение напряжения
(см. рис. 5. кривая 2) – внешняя характеристика
генератора параллельного возбуждения.
Рис. 5

Этим же объясняется
и то, что при постепенном уменьшении
сопротивления нагрузки, ток нагрузки
увеличивается лишь до критического
значения
,
а затем начинает самопроизвольно
уменьшаться до тока короткого замыкания.
При этом напряжение на зажимах генератора
и ток возбуждения резко уменьшаются и
исчезают. Ток короткого замыкания якоря
генератора параллельного возбуждения
определяется только потоком остаточной
намагниченности и поэтому мал.
Рис. 6.

Регулировочная
характеристика – это зависимость тока
возбуждения от тока нагрузки

при
,
и
.

Очень
важной характеристикой генератора
является его КПД

,
(3)

где

– полезная мощность, отдаваемая
генератором;

–мощность
потерь в цепи возбуждения;

–мощность
потерь в цепи якоря.

Формула
(3) для расчета КПД генератора является
приближенной, так как не учитывает
магнитные и механические потери. Обычно
магнитные и механические потери в
генераторах очень малы.

2 Расчет

Программа
работы:

1.) Исследовать и
построить для генератора постоянного
тока независимого возбуждения
характеристики холостого тока, внешнюю,
регулировочную.

2.) Исследовать и
построить для генератора постоянного
тока параллельного возбуждения
характеристики внешнюю, регулировочную.

3.) Рассчитать КПД
генератора.

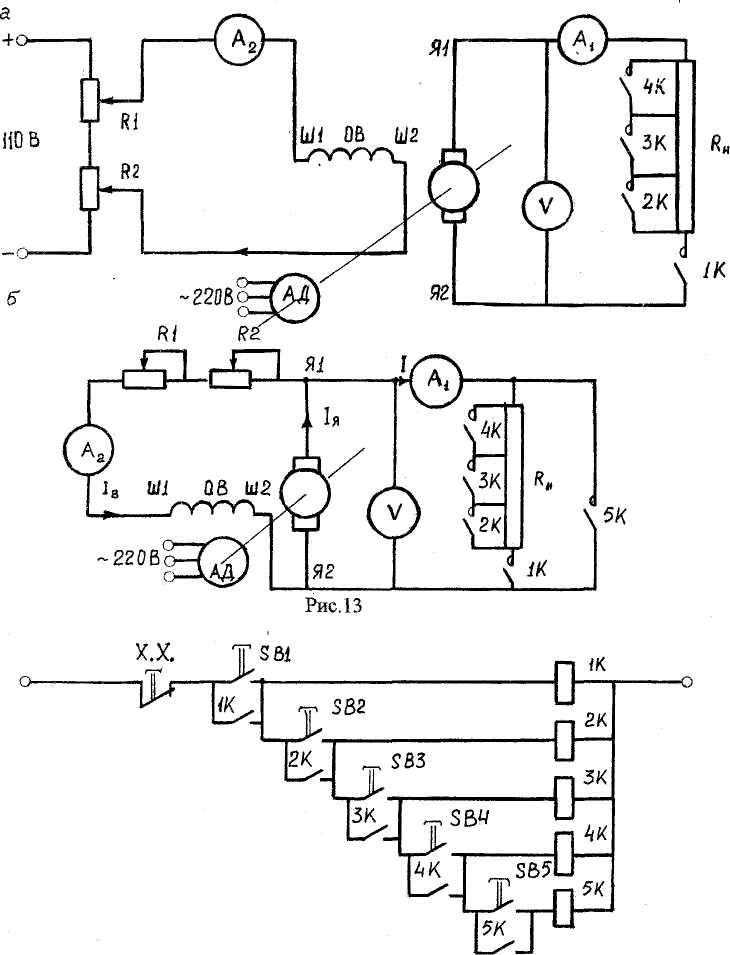
Схема включения
генератора для проведения исследований

Схема для
исследования генератора независимого
возбуждения и снятия его характеристик
приведена на рис. 2.1, а, схема для
исследования генератора параллельного
возбуждения – на рис. 2.1,б. На рис.
2.2 приведена схема управления нагрузкой
генератора.

Оборудование
электрической установки

Лабораторная
установка для исследования свойств
генераторов постоянного тока состоит
из генератора постоянного тока,
включаемого по схеме независимого или
параллельного возбуждения; нагрузочного
реостата Кн, сопротивление которого
изменяется при помощи промежуточных
реле 1К -5К (рис. 2.1); трехфазного
короткозамкнутого асинхронного двигателя
для вращения якоря генератора. Для пуска
в ход асинхронного двигателя на панели
стенда предусмотрена кнопка «пуск»

В цепь возбуждения
генератора включен регулировочный
реостат К1 для изменения тока возбуждения
и амперметр Аг на 2А для его измерения.А1
– амперметр постоянного тока на 30 А для
измерения тока нагрузки;V – вольтметр
постоянного тока на 150 В для измерения
напряжения генератора.

Порядок
выполнения работы

1. Ознакомиться с
машинами, аппаратурой, приборами и
записать технические характеристики
генератора в табл. 1.

Таблица1

Рн,кВт	Uн,В	Iн,А	nн,об/мин	Rя,Ом
0,2	110	246	3000	0,5

2.) Собратьэлектрическую
цепь по схеме (рис.2.1 а).

3.) Снять
характеристику холостого хода: пустить
в ход первичный двигатель нажатием
кнопки «пуск»; записать ЭДС, индуктируемую
в якоре полем остаточной намагниченности
(1В = 0), включить цепь возбуждения
и, не нагружая генератор, постоянно
увеличивать ток возбуждения реостатами
КЛ и К.2 от нуля до возможного максимума.

Рис 2.1

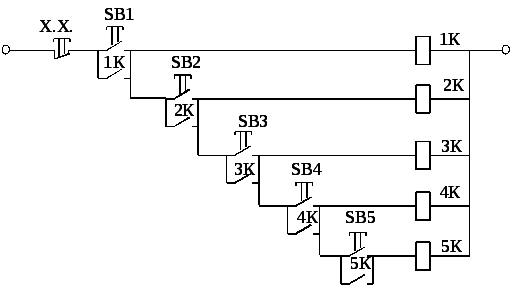
Рис 2.2

Для проведения
опыта короткого замыкания нажать на
несколько секунд кнопку 8В5, после чего
кнопкой “XX” отключить нагрузку.
Показания приборов записать в табл.2

Таблица 2

№,п/п	I,А	Iв,А	U,В
1(хх)
2
3
4
5
6
(кз)

Таблица 3

№ п/п	I,A	Iв,А	А
1
2
3

По данным табл.
5 рассчитать КПД генератора, Заполнить
табл. 4и по ее данным построить график
зависимости КПД от тока нагрузки.

Таблица 4

№ п/п	U,В	I,А	Iв,А	Iя,А	P2,Вт	∆Rя,Вт	∆Rв,Вт	ή	P1,Вт	Pn
1
2
3
4
5
6

Графики

Внешняя
характеристика

110

100

90

80

70

60

40

20

10

1
2 3

Рис. 2.3. График
зависимости U от I

Регулированная
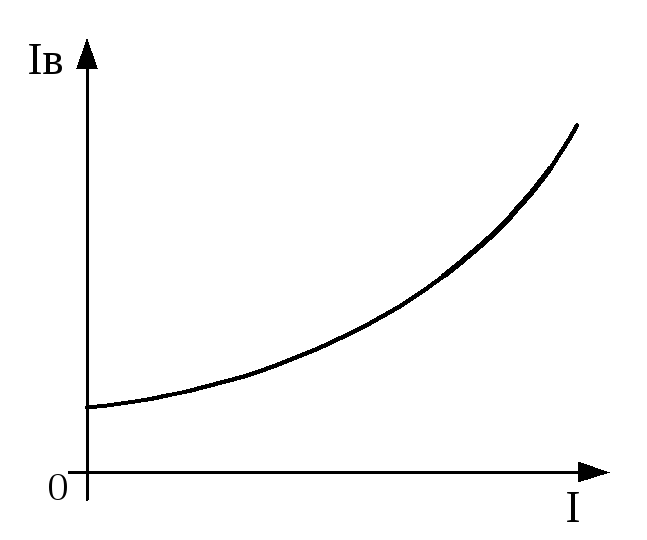
характеристика

Рис. 2.4. График
зависимости IB от I

Рабочие
характеристики

Рис. 2.5. График
зависимости Iя от P2

Механическая
характеристика

1200 –
искусственная

1000

800

–
естественная

600

200

0,5
2 4 7 11,5

Рис. 2.6. График
зависимости n от M

Регулировочная
характеристика двигателя

100

80

60

50

40

20

10

1
2 3 4

Рис. 2.7. Зависимость
частоты вращения от тока возбуждения

3 Контрольные
вопросы

Соседние файлы в папке ellaby

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Коэффициент полезного действия

Зная потери в машине, можно определить коэффициент полез­ного действия (к. п. д.) машины.

а) Коэффициент полезного действия генератора постоянного тока.

Для генераторов к. п. д. представляет собой отношение электрической полезной мощности к механической мощности на валу и определяется по формуле:

Механическую мощность на валу генератора можно представить как:

Электрическая полезная мощность генератора определяется по формуле:

где: ∑P — сумма всех потерь в машине;

U – напряжение на зажимах генератора;

I – ток, отда­ваемый генератором в сеть.

Тогда для генератора коэффициент полезного действия можно определить по формулам:

б) Коэффициент полезного действия двигателя постоянного тока.

Коэффициентом полезного действия двигателя постоянного тока называется отношение механической мощности на валу двигателя Р₂ к подводимой к двигателю электрической мощности Р₁.

В двигателях подводимая мощность Р₁ определяется по формуле:

U – напряжение на зажимах двигателя;

I – ток, потребляемый двигателем.

Механическую мощность на валу двигателя можно представить как:

где: ∑P — сумма всех потерь в машине;

Тогда для двигателя коэффициент полезного действия можно определить по формулам:

Так как к. п. д. машины зависит от суммы потерь, то он – вели­чина непостоянная, т. е. зависит от нагрузки.

При х. х. машин, когда полезная мощность равна нулю, к. п. д. = 0.

По мере увеличения нагрузки к. п. д. машины быстро увеличивается.

Наибольшее значе­ние он имеет при нагрузке, равной (0,8-1) Р_ном когда постоянные потери равны переменным.

При значительных перегрузках вслед­ствие увеличения потерь в сопротивлениях цепи якоря к. п. д. снова снижается.

Рис.20.1. Зависимость к.п.д. машины от нагрузки

Современные элек­трические машины имеют высокий к. п. д.

Так, для машин постоян­ного тока:

мощностью 10 кВт к. п. д. η = 0,83- 0,87;

мощностью 100 кВт; η =0,884-0,93;

мощностью 1000 кВт η = 0,92-0,96.

Маши­ны малой мощности имеют меньшее значе­ние к. п. д., например для двигателя мощ­ностью 10 Вт η = 0,34-0,4

Дата добавления: 2014-12-24 ; просмотров: 2425 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Коэффициент полезного действия (КПД)

О чем эта статья:

КПД: понятие коэффициента полезного действия

Представьте, что вы пришли на работу в офис, выпили кофе, поболтали с коллегами, посмотрели в окно, пообедали, еще посмотрели в окно — вот и день прошел. Если вы не сделали ни одного дела по работе, то можно считать, что ваш коэффициент полезного действия равен нулю.

В обратной ситуации, когда вы сделали все запланированное — КПД равен 100%.

По сути, КПД — это процент полезной работы от работы затраченной.

Вычисляется по формуле:

Формула КПД

η = (A_{полезная}/A_{затраченная}) · 100%

η — коэффициент полезного действия [%]

A_{полезная} — полезная работа [Дж]

A_{затраченная} — затраченная работа [Дж]

Есть такое философское эссе Альбера Камю «Миф о Сизифе». Оно основано на легенде о неком Сизифе, который был наказан за обман. Его приговорили после смерти вечно таскать огромный булыжник вверх на гору, откуда этот булыжник скатывался, после чего Сизиф тащил его обратно в гору. То есть он делал совершенно бесполезное дело с нулевым КПД. Есть даже выражение «Сизифов труд», которое описывает какое-либо бесполезное действие.

Давайте пофантазируем и представим, что Сизифа помиловали и камень с горы не скатился. Тогда, во-первых, Камю бы не написал об этом эссе, потому что никакого бесполезного труда не было. А во-вторых, КПД в таком случае был бы не нулевым.

Полезная работа в этом случае равна приобретенной булыжником потенциальной энергии. Потенциальная энергия прямо пропорционально зависит от высоты: чем выше расположено тело, тем больше его потенциальная энергия. То есть, чем выше Сизиф прикатил камень, тем больше потенциальная энергия, а значит и полезная работа.

Потенциальная энергия

Е_п = mg

Е_п — потенциальная энергия [Дж]

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g ≃ 9,8 м/с 2

Затраченная работа здесь — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

За счет чего происходит процесс?

Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы). Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

КПД в механике

Главный секрет заключается в том, что эта формула подойдет для всех видов КПД.

η = (A_{полезная}/A_{затраченная}) · 100%

η — коэффициент полезного действия [%]

A_{полезная} — полезная работа [Дж]

A_{затраченная} — затраченная работа [Дж]

Дальше мы просто заменяем полезную и затраченную работы на те величины, которые ими являются.

Давайте разберемся на примере задачи.

Задача

Чтобы вкатить санки массой 4 кг в горку длиной 12 метров, мальчик приложил силу в 15 Н. Высота горки равна 2 м. Найти КПД этого процесса. Ускорение свободного падения принять равным g ≃9,8 м/с 2

Запишем формулу КПД.

Теперь задаем два главных вопроса:

Ради чего все это затеяли?

Чтобы санки в горку поднять — то есть ради приобретения телом потенциальной энергии. Значит в данном процессе полезная работа равна потенциальной энергии санок.

Потенциальная энергия

Е_п = mg

Е_п — потенциальная энергия [Дж]

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g ≃ 9,8 м/с 2

За счет чего процесс происходит?

За счет мальчика, он же тянет санки. Значит затраченная работа равна механической работе

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

Заменим формуле КПД полезную работу на потенциальную энергию, а затраченную — на механическую работу:

η = E_п/A · 100% = mgh/FS · 100%

η = 4 · 9,8 · 2/15 · 12 · 100% = 78,4/180 · 100% ≃ 43,6 %

Ответ: КПД процесса приблизительно равен 43,6%

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

КПД в термодинамике

В термодинамике КПД — очень важная величина. Она полностью определяет эффективность такой штуки, как тепловая машина.

• Тепловой двигатель (машина) — это устройство, которое совершает механическую работу циклически за счет энергии, поступающей к нему в ходе теплопередачи.

Схема теплового двигателя выглядит так:

У теплового двигателя обязательно есть нагреватель, который (не может быть!) нагревает рабочее тело, передавая ему количество теплоты Q₁ или Q_{нагревателя} (оба варианта верны, это зависит лишь от учебника, в котором вы нашли формулу).

• Рабочее тело — это тело, на котором завязан процесс (чаще всего это газ или топливо). Оно расширяется при подводе к нему теплоты и сжимается при охлаждении. Часть переданного Q₁ уходит на механическую работу A. Из-за этого производится движение.

Оставшееся количество теплоты Q₂ или Q_{холодильника} отводится к холодильнику, после чего возвращается к нагревателю и процесс повторяется.

КПД такой тепловой машины будет равен:

КПД тепловой машины

η = (A_{полезная}/Q_{нагревателя}) · 100%

η — коэффициент полезного действия [%]

A_{полезная} — полезная работа (механическая) [Дж]

Q_{нагревателя} — количество теплоты, полученное от нагревателя[Дж]

Если мы выразим полезную (механическую) работу через Q_{нагревателя} и Q_{холодильника}, мы получим:

A = Q_{нагревателя} — Q_{холодильника}.

Подставим в числитель и получим такой вариант формулы.

КПД тепловой машины

η = Q_{нагревателя} − Q_{холодильника}/Q_{нагревателя} · 100%

η — коэффициент полезного действия [%]

Q_{нагревателя} — количество теплоты, полученное от нагревателя [Дж]

Q_{холодильника} — количество теплоты, отданное холодильнику [Дж]

А возможно ли создать тепловую машину, которая будет работать только за счет охлаждения одного тела?

Точно нет! Если у нас не будет нагревателя, то просто нечего будет передавать на механическую работу. Любой такой процесс — когда энергия не приходит из ниоткуда — означал бы возможность существования вечного двигателя.

Поскольку свидетельств такого процесса в мире не существует, то мы можем сделать вывод: вечный двигатель невозможен. Это второе начало термодинамики.

Запишем его, чтобы не забыть:

Невозможно создать периодическую тепловую машину за счет охлаждения одного тела без изменений в других телах.

Задача

Найти КПД тепловой машины, если рабочее тело получило от нагревателя 20кДж, а отдало холодильнику 10 кДж.

Решение:

Возьмем формулу для расчета КПД:

η = Q_{нагревателя} − Q_{холодильника}/Q_{нагревателя} · 100%

Решать будем в системе СИ, поэтому переведем значения из килоджоулей в джоули и затем подставим в формулу:

η = 20 000 − 10 000/20 000 · 100% = 50%

Ответ: КПД тепловой машины равен 50%.

Идеальная тепловая машина: цикл Карно

Давайте еще чуть-чуть пофантазируем: какая она — идеальная тепловая машина. Кажется, что это та, у которой КПД равен 100%.

На самом деле понятие «идеальная тепловая машина» уже существует. Это тепловая машина, у которой в качестве рабочего тела взят идеальный газ. Такая тепловая машина работает по циклу Карно. Зависимость давления от объема в этом цикле выглядит следующим образом

А КПД для цикла Карно можно найти через температуры нагревателя и холодильника.

КПД цикла Карно

η = T_{нагревателя} − T_{холодильника} / T_{нагревателя} · 100%

η — коэффициент полезного действия [%]

T_{нагревателя} — температура нагревателя [Дж]

T_{холодильника} — температура холодильника [Дж]

КПД в электродинамике

Мы каждый день пользуемся различными электронными устройствами: от чайника до смартфона, от компьютера до робота-пылесоса — и у каждого устройства можно определить, насколько оно эффективно выполняет задачу, для которой оно предназначено, просто посчитав КПД.

КПД

η = (A_{полезная}/A_{затраченная}) · 100%

η — коэффициент полезного действия [%]

A_{полезная} — полезная работа [Дж]

A_{затраченная} — затраченная работа [Дж]

Для электрических цепей тоже есть нюансы. Давайте разбираться на примере задачи.

Задачка, чтобы разобраться

Найти КПД электрического чайника, если вода в нем приобрела 22176 Дж тепла за 2 минуты, напряжение в сети — 220 В, а сила тока в чайнике 1,4 А.

Решение:

Цель электрического чайника — вскипятить воду. То есть его полезная работа — это количество теплоты, которое пошло на нагревание воды. Оно нам известно, но формулу вспомнить все равно полезно 😉

Количество теплоты, затраченное на нагревание

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг · ˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

Работает чайник, потому что в розетку подключен. Затраченная работа в данном случае — это работа электрического тока.

Работа электрического тока

A = (I 2 ) · Rt = (U 2 )/R · t = UIt

A — работа электрического тока [Дж]

U — напряжение [В]

R — сопротивление [Ом]

То есть в данном случае формула КПД будет иметь вид:

η = Q/A · 100% = Q/UIt · 100%

Переводим минуты в секунды — 2 минуты = 120 секунд. Теперь нам известны все значения, поэтому подставим их:

η = 22176/220 · 1,4 · 120 · 100% = 60%

Ответ: КПД чайника равен 60%.

Давайте выведем еще одну формулу для КПД, которая часто пригождается для электрических цепей, но применима ко всему. Для этого нужна формула работы через мощность:

Работа электрического тока

A — работа электрического тока [Дж]

Подставим эту формулу в числитель и в знаменатель, учитывая, что мощность разная — полезная и затраченная. Поскольку мы всегда говорим об одном процессе, то есть полезная и затраченная работа ограничены одним и тем же промежутком времени, можно сократить время и получить формулу КПД через мощность.

КПД

η = P_{полезная}/P_{затраченная} · 100%

η — коэффициент полезного действия [%]

P_{полезная} — полезная мощность [Дж]

P_{затраченная} — затраченная мощность [Дж]

Коэффициент полезного действия машины постоянного тока

Автор: Евгений Живоглядов.
Дата публикации: 23 января 2013 .
Категория: Статьи.

Общие положения

Коэффициент полезного действия определяется как отношение полезной, или отдаваемой, мощности P₂ к потребляемой мощности P₁:

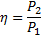(1)

или в процентах

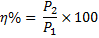(2)

Современные электрические машины имеют высокий коэффициент полезного действия (к. п. д.). Так, у машин постоянного тока мощностью 10 кВт к. п. д. составляет 83 – 87%, мощностью 100 кВт – 88 – 93% и мощностью 1000 кВт – 92 – 96%. Лишь малые машины имеют относительно низкие к. п. д.; например, у двигателя постоянного тока мощностью 10 Вт к. п. д. 30 – 40%.

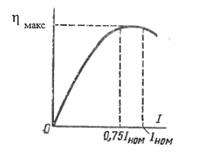
Рисунок 1. Зависимость коэффициента полезного действия электрической машины от нагрузки

Кривая к. п. д. электрической машины η = f(P₂) сначала быстро растет с увеличением нагрузки, затем к. п. д. достигает максимального значения (обычно при нагрузке, близкой к номинальной) и при больших нагрузках уменьшается (рисунок 1). Последнее объясняется тем, что отдельные виды потерь (электрические I_а 2 r_а и добавочные) растут быстрее, чем полезная мощность.

Прямой и косвенный методы определения коэффициента полезного действия

Прямой метод определения к. п. д. по экспериментальным значениям P₁ и P₂ согласно формуле (1) может дать существенную неточность, поскольку, во-первых, P₁ и P₂ являются близкими по значению и, во-вторых, их экспериментальное определение связано с погрешностями. Наибольшие трудности и погрешности вызывает измерение механической мощности.

Если, например, истинные значения мощности P₁ = 1000 кВт и P₂ = 950 кВт могут быть определены с точностью 2%, то вместо истинного значения к. п. д.

Поэтому ГОСТ 25941-83, “Машины электрические вращающиеся. Методы определения потерь и коэффициента полезного действия”, предписывает для машин с η% ≥ 85% косвенный метод определения к. п. д., при котором по экспериментальным данным определяется сумма потерь p_Σ.

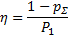(3)

Применив здесь подстановку P₁ = P₂ + p_Σ, получим другой вид формулы:

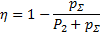(4)

Так как более удобно и точно можно измерять электрические мощности (для двигателей P₁ и для генераторов P₂), то для двигателей более подходящей является формула (3) и для генераторов формула (4). Методы экспериментального определения отдельных потерь и суммы потерь p_Σ описываются в стандартах на электрические машины и в руководствах по испытанию и исследованию электрических машин. Если даже p_Σ определяется со значительно меньшей точностью, чем P₁ или P₂, при использовании вместо выражения (1) формул (3) и (4) получаются все же значительно более точные результаты.

Условия максимума коэффициента полезного действия

Различные виды потерь различным образом зависят от нагрузки. Обычно можно считать, что одни виды потерь остаются постоянными при изменении нагрузки, а другие являются переменными. Например, если генератор постоянного тока работает с постоянной скоростью вращения и постоянным потоком возбуждения, то механические и магнитные потери являются также постоянными. Наоборот, электрические потери в обмотках якоря, добавочных полюсов и компенсационной изменяются пропорционально I_а², а в щеточных контактах – пропорционально I_а. Напряжение генератора при этом также приблизительно постоянно, и поэтому с определенной степенью точности P₂ ∼ I_а.

Таким образом, в общем, несколько идеализированном случае можно положить, что

где коэффициент нагрузки

Определяет относительную величину нагрузки машины.

Суммарные потери также можно выразить через k_нг:

где p₀ – постоянные потери, не зависящие от нагрузки; p₁ – значение потерь, зависящих от первой степени k_нг при номинальной нагрузке; p₂ – значение потерь, зависящих от квадрата k_нг, при номинальной нагрузке.

Подставим P₂ из (5) и p_Σ из (7) в формулу к. п. д.

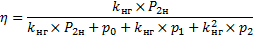(8)

Установим, при каком значении k_нг к. п. д. достигает максимального значения, для чего определим производную dη/dk_нг по формуле (8) и приравняем ее к нулю:

Это уравнение удовлетворяется, когда его знаменатель равен бесконечности, т. е. при k_нг = ∞. Этот случай не представляет интереса. Поэтому необходимо положить равным нулю числитель. При этом получим

Таким образом, к. п. д. будет максимальным при такой нагрузке, при которой переменные потери k_нг² × p₂, зависящие от квадрата нагрузки, становятся равными постоянным потерям p₀.

Значение коэффициента нагрузки при максимуме к. п. д., согласно формуле (9),

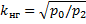(10)

Если машина проектируется для заданного значения η_макс, то, поскольку потери k_нг × p₁ обычно относительно малы, можно считать, что

Изменяя при этом соотношение потерь p₀ и p₂, можно достичь максимального значения к. п. д. при различных нагрузках. Если машина работает большей частью при нагрузках, близких к номинальной, то выгодно, чтобы значение k_нг [смотрите формулу (10)] было близко к единице. Если машина работает в основном при малых нагрузках, то выгодно, чтобы значение k_нг [смотрите формулу (10)] было соответственно меньше.

Источник: Вольдек А. И., “Электрические машины. Учебник для технических учебных заведений” – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.

[spoiler title=”источники:”]

http://skysmart.ru/articles/physics/koefficient-poleznogo-dejstviya-kpd

http://kratko-obo-vsem.ru/articles/820-efficiency-of-electric-machines.html

[/spoiler]

Мощность и потери. Характер подводимой к машине мощности зависит от ее режима работы: у генераторов это механическая мощность P₁ = k₁Mn, у двигателей – электрическая мощность P₁ =UI. Характер снимаемой с машины полезной мощности – противоположный: у генератора это электрическая мощность P₂ = UI, у двигателя – механическая P₂=k₂Mn. В машине всегда есть мощность потерь ∆Р, которая складывается из мощности электрических потерь (потери в меди) ∆Рэл = RI², идущих на нагрев обмоток, мощности магнитных потерь (потери в стали) ∆Рмаг, мощности механических потерь (потери на трение) ∆Рмех и мощности добавочных потерь  ∆Рдоб ≈ 0,01 Рном, где Рном – номинальная мощность. Таким образом, ∆Р = ∆Рмех + ∆Рмаг + ∆Рэл +∆Рдоб и  Р₁ = Р₂ + ∆Р.

КПД машины. КПД машины можно рассчитать по формуле η = P ₂ / P₁. При экспериментальном определении КПД проще и, главное, точнее измерять не механическую мощность, а электрическую, и рассчитывать потери. Поэтому для определения КПД генератора пользуются формулой

η = P₂ / (P₂ + ∆Р)

и КПД двигателя

η = (P₁ —  ∆Р) / Р₁.

КПД машин постоянного тока растет с увеличением мощности машин. Так, у микромашин мощностью до 0,1 кВт он составляет всего 30 – 40 %, у машин мощностью 10 кВт – 83 % и у машин 1000 кВт  —  96 %.

КПД меняется также в зависимости от нагрузки (рис. 1.15). Из графика следует, что при малых нагрузках КПД резко падает, поэтому недогруженную машину невыгодно эксплуатировать.