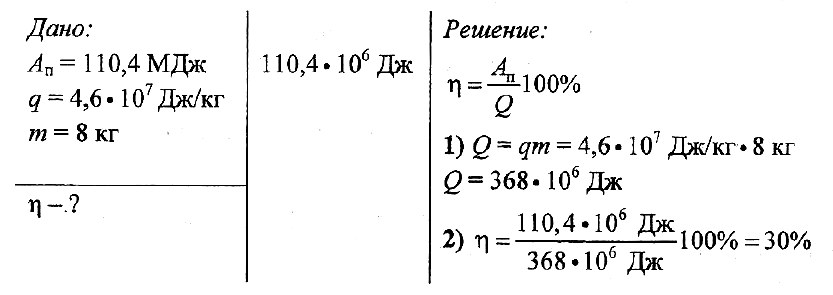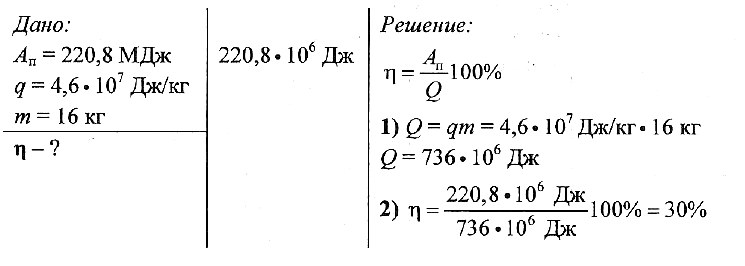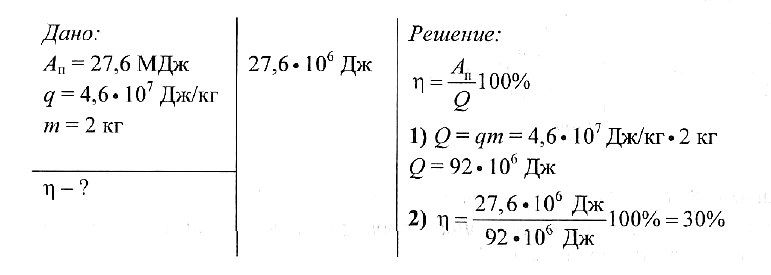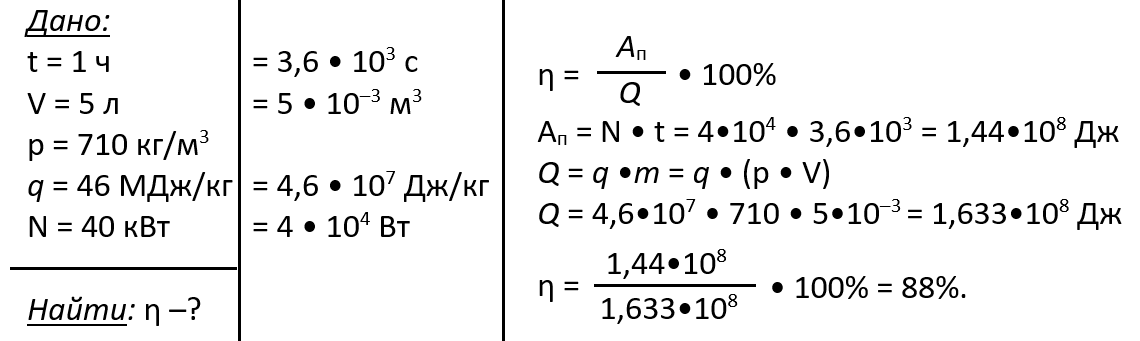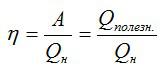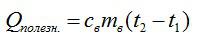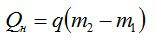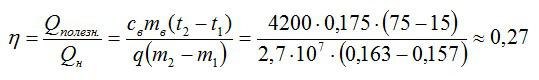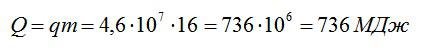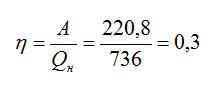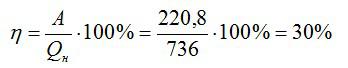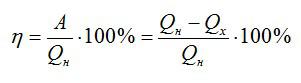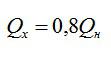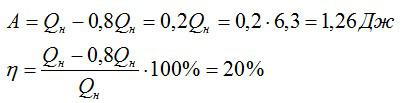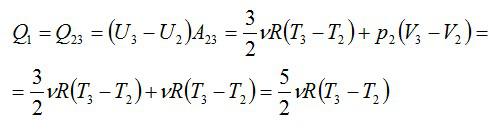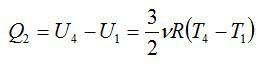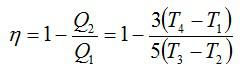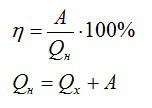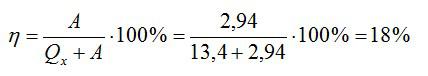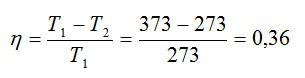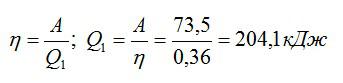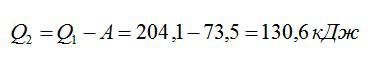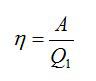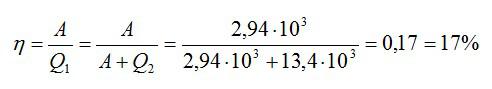Задачи на КПД тепловых двигателей с решениями
Формулы, используемые на уроках «Задачи на КПД тепловых двигателей».
Название величины |
Обозначение |
Единица измерения |
Формула |
Масса топлива |
m |
кг |
|
Удельная теплота сгорания топлива |
q |
Дж/кг |
|
Полезная работа |
Ап |
Дж |
Ап = ɳ Q |
Затраченная энергия |
Q |
Дж |
Q = qm |
КПД |
ɳ |
% |
 |
Относится ли ружьё к тепловым двигателям? Да, так как при выстреле внутренняя энергия топлива превращается в механическую энергию.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Определите КПД двигателя автомобиля, которому для выполнения работы 110,4 МДж потребовалось 8 кг бензина.
Задача № 2.
Определите КПД двигателя автомобиля, которому для выполнения работы 220,8 МДж потребовалось 16 кг бензина.
Задача № 3.
Определите КПД двигателя автомобиля, которому для выполнения работы 27,6 МДж потребовалось 2 кг бензина.
Задача № 4.
На теплоходе установлен дизельный двигатель мощностью 80 кВт с КПД 30%. На сколько километров пути ему хватит 1 т дизельного топлива при скорости движения 20 км/ч? Удельная теплота сгорания дизельного топлива 43 МДж/кг.
Задача № 5.
Патрон травматического пистолета «Оса» 18 x 45 мм, содержит резиновую пулю массой 8,4 г. Определите КПД патрона, если пуля при выстреле приобрела скорость 140 м/с. Масса порохового заряда патрона составляет 0,18 г, удельная теплота сгорания пороха 3,8 • 106 Дж/кг.
Задача № 6.
Первый гусеничный трактор конструкции А. Ф. Блинова, 1888 г., имел два паровых двигателя. За 1 ч он расходовал 5 кг топлива, у которого удельная теплота сгорания равна 30 • 106 Дж/кг. Вычислите КПД трактора, если мощность двигателя его была равна около 1,5 кВт.
Задача № 7.
Двигатель внутреннего сгорания совершил полезную работу, равную 2,3 • 104 кДж, и при этом израсходовал бензин массой 2 кг. Вычислите КПД этого двигателя.
Задача № 8.
За 3 ч пробега автомобиль, КПД которого равен 25%, израсходовал 24 кг бензина. Какую среднюю мощность развивал двигатель автомобиля при этом пробеге?
Задача № 9.
Двигатель внутреннего сгорания мощностью 36 кВт за 1 ч работы израсходовал 14 кг бензина. Определите КПД двигателя.
Задача № 10.
ОГЭ
Идеальная тепловая машина, работающая по циклу Карно, 80 % теплоты, полученной от нагревания, передаёт охладителю. Количество теплоты, получаемое рабочим телом за один цикл от нагревателя, Q1 = 6,3 Дж. Найти КПД цикла ɳ и работу А, совершаемую за один цикл.
Задача № 11.
ЕГЭ
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найти КПД цикла ɳ.
Задача № 12.
Снегоуборочная машина мощностью 40 кВт за 1 час работы расходует примерно 5 л бензина. Каков КПД снегоуборочной машины? Удельная теплота сгорания бензина 46 МДж/кг, плотность бензина — 710 кг/м3.
Краткая теория для решения Задачи на КПД тепловых двигателей.
Это конспект по теме «ЗАДАЧИ на КПД тепловых двигателей». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Закон Ома.
- Посмотреть конспект «Тепловые машины. ДВС. Удельная теплота сгорания».
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
Подставляем значения и вычисляем:
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
Теперь можно рассчитать КПД:
Или, умножая на 100, получаем значение КПД в процентах:
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
По условию:
Вычислим сначала работу, а затем КПД:
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
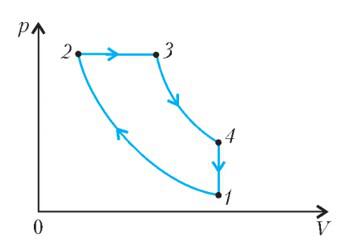
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
Аналогично:
Получим результат:
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
Отсюда:
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:
- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
На этой странице вы узнаете
- В чем прелесть фазовых переходов?
- Что лучше выбрать: Mercedes или BMW?
Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов,а именно получать тепловую энергию различными доступными способами. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне.
Тепловые машины и их КПД
Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.
Вспомним, что фазовые переходы — это переход из одного агрегатного состояния в другое. При этом может выделяться большое количество теплоты.
Именно благодаря этому они и стали такими полезными для нас. Например, в ядерных реакторах воду используют в качестве рабочего тела, то есть она нагревается вследствие энергии, полученной из ядерных реакций, доходит до температуры кипения, а затем под большим давлением уже в качестве водяного пара воздействует на ротор генератора, который вращается и дает нам электроэнергию! На этом основан принцип работы атомных электростанций.
А самый простой пример фазового перехода — образование льда на лужах в морозные ноябрьские дни. Правда о выделении тепла здесь речи не идет.
Мы не почувствуем, как испарится капелька у нас на руке, потому что это не требует много тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. А зачем мы вообще рассматриваем эти фазовые переходы? Все дело в том, что именно фазовые переходы являются ключевым звеном во всех процессах, где нас просят посчитать КПД, от них нашему рабочему телу и подводится теплота нагревателя.

Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.
Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую.
Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в автомобилях часть энергии от сгоревшего бензина идет на движение. Схематично можно изобразить так:
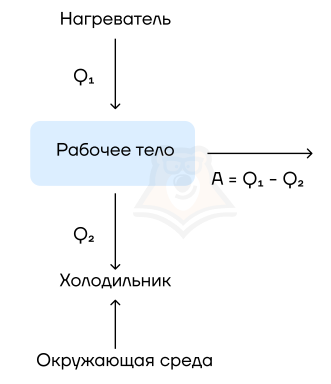
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q1, из которой A уходит на работу механизма. Остаток теплоты Q2 рабочее тело отдает холодильнику, по сути — это потеря энергии.
Физика не была бы такой загадочной, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:
Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
(eta) — КПД,
A — работа газа (Дж),
Q1 — количество теплоты, полученное от нагревателя (Дж).
Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери.
Полезную работу можно расписать как Q1 — Q2 (по закону сохранения энергии). Тогда формула примет вид:
(eta = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})
Давайте попрактикуемся в применении данной формулы на задаче номер 9 из ЕГЭ.
Задача. Тепловая машина, КПД которой равен 60%, за цикл отдает холодильнику 100 Дж. Какое количество теплоты за цикл машина получает от нагревателя? (Ответ дайте в джоулях).
Решение:
Давайте сначала вспомним нашу формулу для КПД:
(eta = frac{Q_1 — Q_2}{Q_1}),
где (Q_1) — это теплота, которую тело получает от нагревателя, (Q_2) — теплота, которая подводится к холодильнику.
Тогда отсюда можно вывести искомую теплоту нагревателя:
(eta Q_1 =Q_1-Q_2)
(eta Q_1 — Q_1= -Q_2)
(Q_1=frac{- Q_2}{eta-1}=frac{-100}{0,6-1}=250 Дж).
Ответ: 250 Дж
Цикл Карно
Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже все сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат. Рассмотрим, как этот цикл выглядит в координатах p(V).
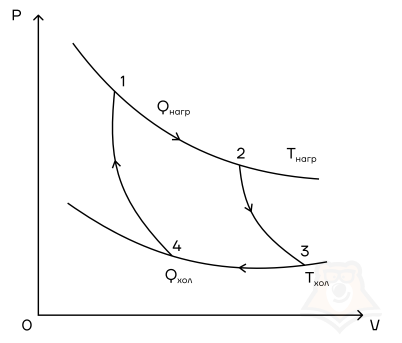
- Температура верхней изотермы 1-2 — температура нагревателя (так как теплота в данном процессе подводится).
- Температура нижней изотермы 3-4 — температура холодильника (так как теплота в данном процессе отводится).
- 2-3 и 4-1 — это адиабатические расширение и сжатие соответственно, в них газ не обменивается теплом с окружающей средой.
Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД.
Формула, по которой можно рассчитать ее КПД выражается через температуры:
T1 — температура нагревателя,
T2 — температура холодильника.
Не то круто, что красиво, а то, что по Карно работает! Поэтому присматривайте такой автомобиль, у которого высокий КПД.
Интересно, что максимальный уровень КПД двигателя внутреннего сгорания автомобилей на данный момент всего около 43%. По официальным заявлениям компания Nissan Motor с 2021 года испытывает прообраз двигателя нового поколения с планируемым КПД 50%.
Приступим к задачам
Задачи на данную тему достаточно часто встречаются в задании 27 из КИМа ЕГЭ. Давайте разберем некоторые примеры.
Задание 1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A12 = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Qхол| = 4780 Дж. Найдите работу газа |A13| на адиабате, если количество вещества постоянно.
Решение:
Шаг 1. Первое, с чего лучше начинать задачи по термодинамике — исследование процессов.
Посмотрим на участок 1-2 графика: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: (frac{pV}{T} = const). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем. Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.
Участок 2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: (frac{p}{T} = const). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.
Участок 3-1: адиабата по условию, то есть количество теплоты в этом переходе равна нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем.
Оформим все данные в таблицу.
Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.

Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.
Шаг 2. Первый закон термодинамики для процесса 1-2 запишется в виде:
Q12 = ΔU12 + A12.
Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции:
(A_{12} = frac{p_0 + 2p_0}{2} * V0 =frac{3p_0V_0}{2}).
Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:
(Delta U_{12} = frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = frac{9p_0V_0}{2}).
Заметим, что это в 3 раза больше работы газа на этом участке:
(Delta U_{12} = 3A_{12} rightarrow Q_{12} = 4A_{12}).
Шаг 3. Работа цикла — площадь фигуры, которую замыкает график, тогда . A = A12 — |A31|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q12 — |Q31|.
Сравним эти формулы:
Q12 -|Q31| = A12 — |A31|,
подставим выражения из предыдущего пункта:
4A12 — |Q31| = A12 — |A31| (rightarrow) |A31| = -3A12 + |Q31| = -31520 + 4780 = 220 Дж.
Ответ: 220 Дж
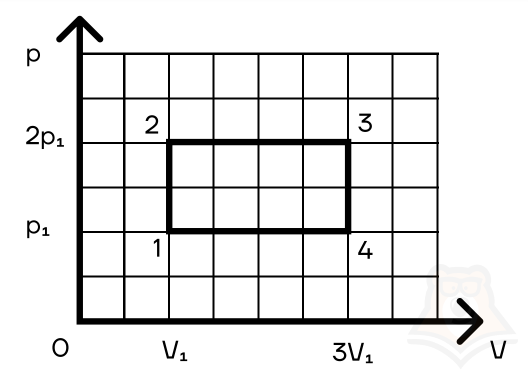
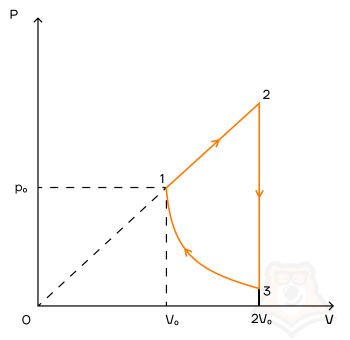
Задание 2. Найти КПД цикла для идеального одноатомного газа.
Решение:
Шаг 1. КПД цикла определим по формуле: (eta = frac{A}{Q}), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p1 — p1)(3V1 — V1) = 2p1V1.
Шаг 2. Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:
Посмотрим на участок 1-2 графика: давление растет, объем не меняется. По закону Шарля (frac{p}{T} = const) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.
2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака (frac{V}{T} = const) температура тоже растет, растет и внутренняя энергия.
3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.
4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.
Оформим данные в таблицу:
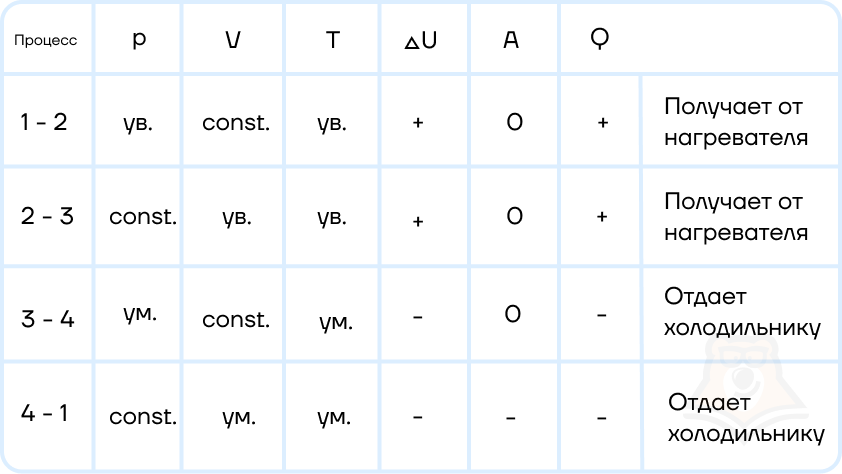
Отметим, что необходимое Q = Q12 + Q23.
Шаг 3. Запишем первый закон термодинамики для процессов 1-2 и 2-3:
(Q_{12} = U_{12} + A_{12} = Delta U_{12} = frac{3}{2}(2p_1V_1 -p_1V_1) = frac{3}{2}p_1V_1).
(Q_{23} = Delta U_{23} + A_{23}), работу газа найдем как площадь под графиком: A23 = 2p1(3V1 — V1) = 4p1V1.
(Delta U_{12} = frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1).
(Q_{23} = Delta U_{23} + A_{23} = 10p_1V_1).
Шаг 4. Мы готовы считать КПД: (eta = frac{A}{Q} = frac{A}{Q_{12} + Q_{23}} = frac{2p_1V_1}{frac{3}{2}p_1V_1 + 10p_1V_1} = frac{4}{23} approx 0,17).
Ответ: 17%
Теперь вас не должно настораживать наличие графиков в условиях задач на расчет КПД тепловых машин. Продолжить обучение решению задач экзамена вы можете в статьях «Применение законов Ньютона» и «Движение точки по окружности».
Фактчек
- Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую.
- Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
- Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
(eta = frac{A}{Q_1} = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1}) - Цикл Карно — цикл с максимально возможным КПД: (eta = frac{T_1 — T_2}{T_1} = 1 — frac{T_2}{T_1})
- Не забываем, что работа считается, как площадь фигуры под графиком.
Проверь себя
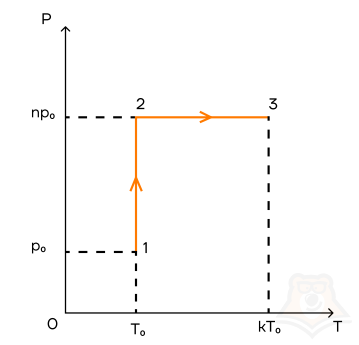
Задание 1.
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T0 = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.
- 5672 Дж
- 4731 Дж
- 5817 Дж
- 6393 Дж
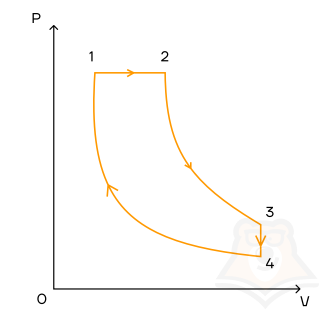
Задание 2.
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT12 к изменению его температуры ΔT34 при изохорном процессе равен 1,5. Определите КПД цикла.
- 0,6
- 0,5
- 0,8
- 1
Задание 3.
В топке паровой машины сгорело 50 кг каменного угля, удельная теплота сгорания которого равна 30 МДж/кг. При этом машиной была совершена полезная механическая работа 135 МДж. Чему равен КПД этой тепловой машины? Ответ дайте в процентах.
- 6%
- 100%
- 22%
- 9%
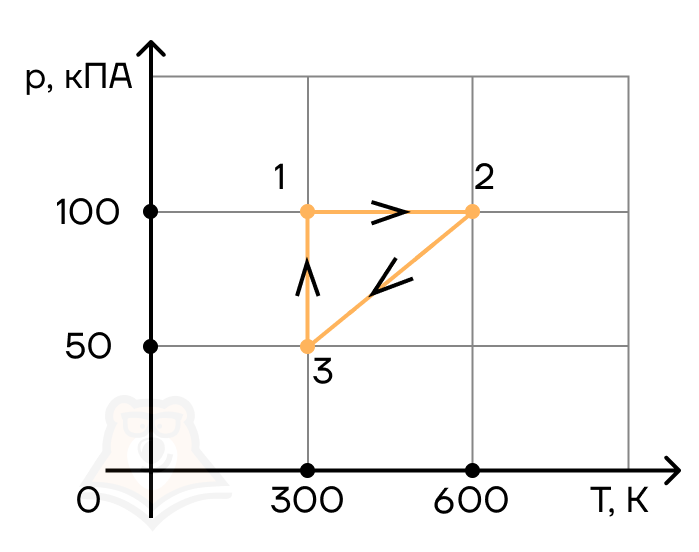
Задание 4.
С двумя молями одноатомного идеального газа совершают циклический процесс 1–2–3–1 (см. рис.). Чему равна работа, совершаемая газом на участке 1–2 в этом циклическом процессе?
- 4444 Дж
- 2891 Дж
- 4986 Дж
- 9355 Дж
Ответы:1 — 3; 2 — 1; 3 — 4; 4 — 3.
КПД теплового двигателя рассчитывается по формуле $eta = frac{A_п}{Q_1}$ или $eta = frac{Q_1 — Q_2}{Q_1} cdot 100 %$, где
$A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику.
Когда говорят о коэффициенте полезного действия теплового двигателя, часто используют понятие мощности или полезной мощности: $N = frac{A_п}{t}$. Эту величину в жизни использовать удобнее, чем говорить о полезной работе.
На данном уроке мы разберем решение задач, используя формулы, приведенные выше.
Для решения задач, в условиях которых, говорится о сжигании топлива ($Q = qm$), вам понадобятся табличные значения удельной теплоты сгорания топлива.
Задача №1
Какая работа совершена внешними силами при обработке железной заготовки массой $300 space г$, если она нагрелась на $200 degree C$?
Дано:
$m = 300 space г$
$Delta t = 200 degree C$
$c = 460 frac{Дж}{кг cdot degree C}$
СИ:
$m = 0.3 space кг$
$A — ?$
Показать решение и ответ
Скрыть
Решение:
Для того чтобы нагреть железную деталь, необходимо сообщить ей некоторое количество теплоты:
$Q = cm(t_2 — t_1) = cm Delta t$.
Рассчитаем эту энергию:
$Q = 460 frac{Дж}{кг cdot degree C} cdot 0.3 space кг cdot 200 degree C = 27 space 600 space Дж = 27.6 space кДж$.
Сообщенная энергия будет эквивалентна работе внешних сил:
$A = Q = 27.6 space кДж$.
Ответ: $A = 27.6 space кДж$.
Задача №2
Приняв, что вся тепловая энергия угля обращается в полезную работу, рассчитайте какого количества каменного угля в час достаточно для машины мощностью $733 space Вт$?
Дано:
$t = 1 space ч$
$N = 733 space Вт$
$q = 2.7 cdot 10^7 frac{Дж}{кг}$
СИ:
$t = 3600 space с$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Мощность по определению:
$N = frac{A_п}{t}$.
Выразим отсюда полезную работу, совершаемую машиной, и рассчитаем ее:
$A_п = Nt$,
$A_п = 733 space Вт cdot 3600 space с = 2 space 638 space 800 space Дж approx 0.26 cdot 10^7 space Дж$.
По условиям задачи количество теплоты, которое выделяется при сжигании каменного угля, равно полезной работе:
$A_п = Q = qm$.
Выразим отсюда массу угля и рассчитаем ее:
$m = frac{A_п}{q}$,
$m = frac{0.26 cdot 10^7 space Дж}{2.7 cdot 10^7 frac{Дж}{кг}} approx 0.1 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №3
Нагреватель за некоторое время отдает тепловому двигателю количество теплоты, равное $120 space кДж$. Тепловой двигатель совершает при этом полезную работу $30 space кДж$. Определите КПД теплового двигателя.
Дано:
$Q_1 = 120 space кДж$
$A_п = 30 space кДж$
СИ:
$Q_1 = 120 cdot 10^3 space Дж$
$A_п = 30 cdot 10^3 space Дж$
$eta — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1}$.
Рассчитаем:
$eta = frac{30 cdot 10^3 space Дж}{120 cdot 10^3 space Дж} = 0.25$,
или в процентах $eta = 25 %$.
Ответ: $eta = 25 %$.
Задача №4
Нагреватель отдает тепловому двигателю за $30 space мин$ количество теплоты, равное $460 space МДж$, а тепловой двигатель отдает количество теплоты, равное $280 space МДж$. Определите полезную мощность двигателя.
Дано:
$t = 30 space мин$
$Q_1 = 460 space МДж$
$Q_2 = 280 space МДж$
СИ:
$t = 1800 space с$
$Q_1 = 460 cdot 10^6 space Дж$
$Q_2 = 280 cdot 10^6 space Дж$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = =frac{A_п}{Q_1} = frac{Q_1 — Q_2}{Q_1}$, где
$A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику.
Из этой формулы, мы можем сделать вывод, что $Q_1 — Q_2 = A_п$ — количество теплоты, которое пошло на совершение работы.
Величина работы также присутствует в определении мощности:
$N = frac{A_п}{t}$.
Когда мощность определяется полезной работой, мы называем ее полезной мощностью.
Подставим в формулу мощности определение работы из формулы для КПД и рассчитаем ее:
$N = frac{Q_1 — Q_2}{t}$,
$N = frac{460 cdot 10^6 space Дж — 280 cdot 10^6 space Дж}{1800 space с} = frac{180 cdot 10^6 space Дж}{1800 space с} = 0.1 cdot 10^6 space Вт = 100 space кВт$.
Ответ: $N = 100 space кВт$.
Задача №5
Паровой молот мощностью $367 space кВт$ получает от нагревателя в час количество теплоты, равное $6720 space МДж$. Какое количество теплоты в час получает холодильник?
Дано:
$N = 367 space кВт$
$t = 1 space ч$
$Q_1 = 6720 space МДж$
СИ:
$N = 367 cdot 10^3 space Вт$
$t = 3600 space с$
$Q_1 = 6720 cdot 10^6 space Дж$
$Q_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Полезная работа, совершенная тепловым двигателем, определяется разностью количества теплоты, отданному холодильнику, и количества теплоты, полученного от нагревателя:
$A_п = Q_1 — Q_2$.
Тогда, количество теплоты, которое получает холодильник будет равно:
$Q_2 = Q_1 — A_п$.
Совершенную работу мы можем определить через мощность:
$N = frac{A_п}{t}$,
$A_п = Nt$.
Подставим в формулу для количества теплоты, получаемого холодильником:
$Q_2 = Q_1 — Nt$.
Рассчитаем эту энергию:
$Q_2 = 6720 cdot 10^6 space Дж — 367 cdot 10^3 space Вт cdot 3600 space с = 6720 cdot 10^6 space Дж — 1321.2 cdot 10^6 space Дж = 5398.8 cdot 10^6 space Дж approx 5400 space МДж$.
Ответ: $Q_2 approx 5400 space МДж$.
Задача №6
Мопед, едущий со скоростью $20 frac{км}{ч}$, за $100 space км$ пути расходует $1 space кг$ бензина. КПД его двигателя равен $22 %$. Какова полезная мощность двигателя?
Дано:
$upsilon = 20 frac{км}{ч}$
$s = 100 space км$
$m = 1 space кг$
$eta = 22 % = 0.22$
$q = 4.6 cdot 10^7 frac{Дж}{кг}$
СИ:
$upsilon approx 5.6 frac{м}{с}$
$s = 100 cdot 10^3 space м$
$N — ?$
Показать решение и ответ
Скрыть
Решение:
Мощность по определению:
$N = frac{A_п}{t}$.
Полезную работу мы можем выразить из формулы для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1}$.
Количество теплоты $Q_1$, выделившееся при сгорании бензина, мы можем найти по формуле:
$Q = qm$.
Подставим в формулу для расчета КПД:
$eta = frac{A_п}{qm}$.
Выразим отсюда полезную работу:
$A_п = eta cdot qm$.
Время, которое необходимо нам для расчета мощности, мы можем найти через перемещение и скорость:
$t = frac{s}{upsilon}$.
Подставим найденные формулы для величин $A_п$ и $t$ в формулу для расчета мощности:
$N = frac{eta cdot qm}{frac{s}{upsilon}} = frac{eta cdot qm cdot upsilon}{s}$.
Рассчитаем эту мощность:
$N = frac{0.22 cdot 4.6 cdot 10^7 frac{Дж}{кг} cdot 1 space кг cdot 5.6 frac{м}{с}}{100 cdot 10^3 space м} approx frac{5.67 cdot 10^7 space Дж cdot с}{0.01 cdot 10^7} approx 567 space Вт$.
Ответ: $N approx 567 space Вт$.
Задача №7
Определите КПД двигателя внутреннего сгорания мощностью $36.6 space кВт$, который сжигает в течение одного часа $10 space кг$ нефти.
Дано:
$N = 36.6 space кВт$
$t = 1 space ч$
$m = 10 space кг$
$q = 4.4 cdot 10^7 frac{Дж}{кг}$
СИ:
$N = 36.6 cdot 10^3 space Вт$
$t = 3600 space с$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1} cdot 100 %$.
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты $Q_1$, полученное от нагревателя, — это энергия, которая выделится при сгорании топлива:
$Q_1 = qm$.
Подставим эти выражения в формулу КПД и рассчитаем его:
$eta = frac{Nt}{qm} cdot 100%$,
$eta = frac{36.6 cdot 10^3 space Вт cdot 3600 space с}{4.4 cdot 10^7 frac{Дж}{кг} cdot 10 space кг} cdot 100 % = frac{13.176 cdot 10^7 space Дж}{44 cdot 10^7 space Дж} cdot 100 % approx 30 %$.
Ответ: $eta approx 30 %$.
Паровая машина мощностью $220 space кВт$ имеет КПД $15 %$. Сколько каменного угля сгорает в ее топке за $8 space ч$?
Дано:
$N = 220 space кВт$
$t = 8 space ч$
$eta = 15 % = 0.15$
$q = 2.7 cdot 10^7 frac{Дж}{кг}$
СИ:
$N = 220 cdot 10^3 space Вт$
$t = 28.8 cdot 10^3 space с$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД:
$eta = frac{A_п}{Q_1}$.
Полезную работу $A_п$ мы можем выразить через мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты, полученное от нагревателя — это энергия, выделившаяся при сгорании каменного угля:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$eta = frac{Nt}{qm}$.
Выразим отсюда массу каменного угля:
$m = frac{Nt}{q eta}$.
Рассчитаем ее:
$m = frac{220 cdot 10^3 space Вт cdot 28.8 cdot 10^3 space с}{2.7 cdot 10^7 frac{Дж}{кг} cdot 0.15} = frac{633.6 cdot 10^7 space Дж}{0.405 cdot 10^7 frac{Дж}{кг}} approx 1564 space кг$.
Ответ: $m approx 1564 space кг$.
Задача №9
Современные паровые механизмы расходуют $12.57 space МДж$ в час на $735 space Вт$. Вычислите КПД таких механизмов.
Дано:
$Q_1 = 12.57 space МДж$
$t = 1 space ч$
$N = 735 space Вт$
СИ:
$Q_1 = 12.57 cdot 10^6 space Дж$
$t = 3600 space с$
$eta- ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1} cdot 100 %$.
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты $Q_1$, полученное от нагревателя, нам дано в условиях задачи.
Подставим выражение для полезной работы в формула для КПД и рассчитаем его:
$eta = frac{Nt}{Q_1} cdot 100 %$,
$eta = frac{735 space Вт cdot 3600 space с}{12.57 cdot 10^6 space Дж} cdot 100 % approx 21 %$.
Ответ: $eta approx 21 %$.
Задача №10
Мощность дизельного двигателя $367 space кВт$, КПД $30 %$. На сколько суток непрерывной работы хватит запаса нефти $60 space т$ такому двигателю?
Дано:
$N = 367 space кВт$
$m = 60 space т$
$eta = 30 % = 0.3$
$q = 4.4 cdot 10^7 frac{Дж}{кг}$
СИ:
$N = 367 cdot 10^3 space Вт$
$m = 60 cdot 10^3 space кг$
$t — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1}$.
Полезную работу $A_п$ мы можем выразить через мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты, полученное от нагревателя — это энергия, выделившаяся при сгорании нефти:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$eta = frac{Nt}{qm}$.
Выразим отсюда время, за которое была совершена полезная работа:
$t = frac{qm eta}{N}$.
Рассчитаем его:
$t = frac{4.4 cdot 10^7 frac{Дж}{кг} cdot 60 cdot 10^3 space кг cdot 0.3}{367 cdot 10^3 space Вт} = frac{79.2 cdot 10^7 space Дж}{367 space Вт} approx 2.16 cdot 10^6 space с$.
Переведем в сутки. В одном дне $60 cdot 60 cdot 24 space с = 86 space 400 space с$. Тогда,
$t = frac{2.16 cdot 10^6}{86 space 400} = 25 space сут$.
Ответ: $t = 25 space сут$.
п.1. Полезная работа и затраченная работа
Полезной называется работа по подъёму грузов или преодолению какого-либо сопротивления.
Затраченной (полной) называется работа, совершённая приложенной силой.
Примеры полной и полезной работы
Затраченная работа равна сумме:
- полезной работы;
- работы против силы трения в различных частях механизма;
- работы по перемещению различных составных элементов механизма.
Поэтому всегда (A_text{полезная}lt A_text{затраченная})
п.2. КПД механизма
Коэффициент полезного действия механизма – это отношение его полезной работы к затраченной работе. $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%} $$
Поскольку в реальных механизмах всегда (A_text{п}lt A_text{з}), $$ frac{A_text{п}}{A_text{з}}lt 1. $$
Следовательно КПД реальных механизмов (etalt 100text{%}).
Только в идеальном механизме, в котором нет потерь на трение, и все составные элементы не имеют веса, (A_text{п}=A_text{з}) и (eta=100text{%}).
КПД никогда не может быть выше (100text{%}).
КПД реальных механизмов можно увеличить за счет снижения трение в подвижных узлах и уменьшения веса всех составных элементов конструкции.
Для этого нужны новые смазочные вещества и лёгкие, но прочные конструкционные материалы.
п.3. Задачи
Задача 1. По наклонной плоскости поднимают груз массой 50 кг, прикладывая к нему силу 250 Н, направленную вдоль плоскости. Чему равен КПД плоскости, если её длина 10 м, а высота 3 м?
Дано:
(m=50 text{кг})
(gapprox 10 text{м/с}^2)
(F=250 text{Н})
(L=10 text{м})
(h=3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза begin{gather*} A_text{п}=mgh. end{gather*} Затраченная работа на перемещение груза вдоль наклонной плоскости begin{gather*} A_text{з}=FL. end{gather*} КПД плоскости: begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{FL}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{50cdot 10cdot 3}{250cdot 10}cdot 100text{%}=60text{%} end{gather*} Ответ: 60%
Задача 2. С помощью подвижного блока поднимают груз массой 200 кг, прикладывая силу 1200 Н. Чему равен КПД блока?
Дано:
(m=200 text{кг})
(gapprox 10 text{м/с}^2)
(F=1200 text{Н})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза и проигрыш в расстоянии. Т.е. при работе нужно вытянуть трос длиной (2h). Затраченная работа: begin{gather*} A_text{з}=Fcdot 2h. end{gather*} КПД блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{2Fh}cdot 100text{%}=frac{mg}{2F}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{200cdot 10}{2cdot 1200}cdot 100text{%}approx 83,3text{%} end{gather*} Ответ: 83,3%
Задача 3. Груз массой 245 кг с помощью рычага равномерно подняли на высоту 6 см. При этом к длинному плечу рычага была приложена сила 500 Н, а точка приложения силы опустилась на 30 см. Найдите КПД рычага.
Дано:
(m=245 text{кг})
(gapprox 10 text{м/с}^2)
(h_2=6 text{см}=0,6 text{м})
(F_1=500 text{Н})
(h_1=30 text{см}=0,3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию длинного плеча рычага: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД рычага begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{245cdot 10cdot 0,06}{500cdot 0,3}cdot 100text{%}=frac{147}{150}cdot 100text{%}=98text{%} end{gather*} Ответ: 98%
Задача 4. Чему равен КПД гидравлической машины, если для равномерного подъема груза массой 1,2 т к меньшему поршню прикладывают силу 160 Н? Площади поршней равны 5 см2 и 500 см2.
Дано:
(m=1,2 text{т}=1200 text{кг})
(gapprox 10 text{м/с}^2)
(F_1=160 text{Н})
(S_1=5 text{см}^2=5cdot 10^{-4} text{м}^2)
(S_2=500 text{см}^2=5cdot 10^{-2} text{м}^2)
__________________
(eta-?)
При опускании малого поршня на высоту (h_1) из малого в большой цилиндр вытекает объем жидкости равный $$ V=S_1h_1=S_2h_2Rightarrow frac{h_2}{h_1}=frac{S_1}{S_2} $$ Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию поршня малого цилиндра: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД гидравлической машины begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%}=frac{mgS_1}{F_1S_2}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{1200cdot 10cdot 5cdot 10^{-4}}{160cdot 5cdot 10^{-2}}cdot 100text{%}=frac{600}{800}cdot 100text{%}=75text{%} end{gather*} Ответ: 75%
Задача 5*. Груз массой 12 кг поднимают с помощью подвижного блока массой 3 кг. Чему равен КПД блока?
Дано:
(M=12 text{кг})
(m=3 text{кг})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза. Поэтому достаточно приложить силу, равную половине суммы весов груза и блока: begin{gather*} F=frac 12(M+m)g end{gather*} При этом будет проигрыш в расстоянии. Потребуется вытянуть трос длиной (2h). Затраченная работа, приложенная к тросу: begin{gather*} A_text{з}=Fcdot 2h=frac 12(M+m)gcdot 2h=(M+m)gh. end{gather*} КПД подвижного блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Mgh}{(M+m)gh}cdot 100text{%}=frac{M}{M+m}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{12}{12+3}cdot 100text{%}=80text{%} end{gather*} Ответ: 80%
Задача 6. Сколько воды можно поднять из колодца глубиной 36 м за 1 ч, если мощность электродвигателя равна 5 кВт, КПД всей установки равно 70%?
Дано:
(N=5 text{кВт}=5cdot 10^3 text{Вт})
(eta=70text{%}=0,7)
(h=36 text{м})
(t=1 text{ч}=3600 text{с})
(gapprox 10 text{м/с}^2)
__________________
(m-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Затраченная работа электродвигателя: begin{gather*} A_text{з}=Nt. end{gather*} КПД установки begin{gather*} eta=frac{A_text{п}}{A_text{з}}=frac{mgh}{Nt} end{gather*} Масса воды begin{gather*} m=frac{eta Nt}{gh} end{gather*} Получаем: begin{gather*} m=frac{0,7cdot 5cdot 10^3cdot 3600}{10cdot 36}=35cdot 10^3 (text{кг})=35 text{т} end{gather*} Ответ: 35 т
Задача 7*. КПД подвижного блока при подъеме первого груза равен 80%, а при подъеме второго груза – 90%. Масса какого груза больше и во сколько раз? Трением в блоке можно пренебречь.
Дано:
(eta_1=80text{%}=0,8)
(eta_2=90text{%}=0,9)
__________________
(frac{M_2}{M_1}-?)
КПД подвижного блока массой (m), с помощью которого поднимают груз массой (M) begin{gather*} eta=frac{M}{M+m} end{gather*} (см. Задачу 5 выше). Масса груза begin{gather*} eta(M+m)=MRightarrow eta m=(1-eta)MRightarrow M=frac{eta}{1-eta}m end{gather*} Получаем: begin{gather*} M_1=frac{0,8}{1-0,8}m=4m,\[6pt] M_2=frac{0,9}{1-0,9}m=9m end{gather*} Масса второго груза больше.
Отношение масс begin{gather*} frac{M_2}{M_1}=frac{9m}{4m}=2,25 (text{раз}) end{gather*} Ответ: масса второго груза больше в 2,25 раз
п.4. Лабораторная работа №13. Определение КПД наклонной плоскости
Цель работы
Научиться проводить измерения и рассчитывать КПД простого механизма на примере наклонной плоскости. Исследовать зависимость КПД наклонной плоскости от высоты.
Теоретические сведения
Работа по подъему тела весом (P) вертикально на высоту (h) (из точки C в точку B): $$ A_text{CB}=Ph $$
Работа по перемещению того же тела силой (F), направленной вдоль наклонной плоскости длиной (L) (из точки A в точку B): $$ A_text{AB}=FL $$
В обоих случаях тело перемещается с нулевого уровня AC, где (h_0=0), на уровень с высотой (h) в точку B. Работа сторонних сил в этом случае равна изменению потенциальной энергии тела: $$ A=A_text{CB}=A_text{AB}=Delta E_p $$
Получаем уравнение для идеальной наклонной плоскости (без трения): $$ Ph=FL $$
При наличии трения получаем неравенство: $$ Phlt FL $$
Полезная и затраченная работа для наклонной плоскости: $$ A_text{п}=Ph, A_text{з}=FL $$
КПД наклонной плоскости: $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Ph}{FL}cdot 100text{%} $$
Затраченная работа равна сумме полезной работы и работы по преодолению силы трения: $$ A_text{з}=A_text{п}+F_text{тр}L $$
Откуда сила трения равна: $$ F_text{тр}=frac{A_text{з}-A_text{п}}{L}=frac{FL-Ph}{L}=F-Pfrac hL $$
Вес (P) и сила (F) определяются в работе с помощью динамометра с ценой деления (d=0,1 text{Н}).
Абсолютная погрешность прямых измерений $$ Delta_F=Delta_P=frac d2=0,05 text{Н}. $$
Сила (F) определяется в серии из пяти опытов с вычислением средних величин.
Высота наклонной плоскости (h) и длина наклонной плоскости (L) определяются с помощью мерной ленты с ценой деления (d=5 text{мм}). Абсолютная погрешность (Delta_L=2,5 text{мм}).
Относительные погрешности измерений вычисляются как обычно.
Относительная погрешность расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L $$
Абсолютная погрешность расчета КПД: $$ Delta_eta=etacdot delta_eta $$
Приборы и материалы
Доска длиной от 70 см, штатив с муфтой и лапкой, брусок массой не менее 300 г, мерная лента, динамометр.
Ход работы
1. Измерьте мерной лентой длину доски (L).
2. Определите вес бруска (P) с помощью динамометра.
3. Соберите наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L3.)
4. Положите брусок на наклонную плоскость, прикрепите к нему динамометр и равномерно тяните по наклонной плоскости. Следите, чтобы динамометр располагался параллельно наклонной плоскости. Запишите измеренное значение (F). Повторите измерение (F) в серии из пяти опытов.
5. Соберите новую наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L4). Перейдите на шаг 4 и повторите серию опытов для определения (F).
6. Рассчитайте КПД для двух исследованных наклонных плоскостей. Найдите относительные и абсолютные погрешности расчетов КПД.
7. Для каждой из наклонных плоскостей укажите величину полезной и затраченной работы, найдите силу трения.
8. Сделайте выводы о зависимости силы трения и КПД от высоты наклонной плоскости.
Результаты измерений и вычислений
Длина наклонной плоскости (доски) begin{gather*} L=80 text{см}=800 text{мм},\[7pt] Delta_L=2,5 text{мм},\[6pt] delta_L=frac{Delta_L}{L}=frac{2,5}{800}approx 0,0031=0,31text{%} end{gather*}
Вес бруска begin{gather*} P=4,4 text{Н},\[7pt] Delta_P=0,05 text{Н},\[6pt] delta_P=frac{Delta_P}{P}=frac{0,05}{4,4}approx 0,0011=1,1text{%} end{gather*}
1. Наклонная плоскость высотой (h=27 text{см})
Высота наклонной плоскости begin{gather*} h=27 text{см}=270 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{270}approx 0,0093=0,93text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,9 | 2,8 | 3,0 | 2,7 | 2,8 | 14,2 |
| $$ Delta_F, H $$ | 0,06 | 0,04 | 0,16 | 0,14 | 0,04 | 0,44 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{14,2}{5}=2,84 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,44}{5}approx 0,09 (text{Н}),\[6pt] F=(2,84pm 0,09) text{Н},\[7pt] delta_F=frac{0,09}{2,84}approx 0,032=3,2text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,27=1,188 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,84cdot 0,8=2,272 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,84-4,4cdot frac{0,27}{0,8}approx 1,36 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{1,188}{2,272}approx 0,523=52,3text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,032+0,011+0,0093+0,0031=0,0554approx 0,056=5,6text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,523cdot 0,056approx 0,029=2,9text{%} $$
Окончательно получаем: $$ eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%} $$
2. Наклонная плоскость высотой (h=20 text{см})
Высота наклонной плоскости begin{gather*} h=20 text{см}=200 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{200}approx 0,013=1,3text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,4 | 2,6 | 2,5 | 2,6 | 2,5 | 12,6 |
| $$ Delta_F, H $$ | 0,12 | 0,08 | 0,02 | 0,08 | 0,02 | 0,32 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{12,6}{5}=2,52 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,32}{5}approx 0,06 (text{Н}),\[6pt] F=(2,52pm 0,06) text{Н},\[7pt] delta_F=frac{0,06}{2,52}approx 0,024=2,4text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,2=0,88 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,52cdot 0,8=2,016 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,52-4,4cdot frac{0,2}{0,8}approx 1,42 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{0,88}{2,016}approx 0,437=43,7text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,024+0,011+0,013+0,0031=0,0511approx 0,052=5,2text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,437cdot 0,052approx 0,023=2,3text{%} $$
Окончательно получаем: $$ eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%} $$
Выводы
На основании полученных результатов можно сделать следующие выводы.
В работе проводился расчет КПД наклонной плоскости постоянной длины, но разной высоты.
Для высоты около (h=frac L3):
- полезная и затраченная работы: (A_text{П}=1,188 (text{Дж}), A_text{З}=2,272 (text{Дж}))
- сила трения: (F_text{тр}=1,36 (text{Н}))
- КПД: (eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%})
Для высоты около (h=frac L4):
- полезная и затраченная работы: (A_text{П}=0,88 (text{Дж}), A_text{З}=2,016 (text{Дж}))
- сила трения: (F_text{тр}=1,42 (text{Н}))
- КПД: (eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%})
Таким образом, с уменьшением высоты:
- сила трения растет;
- КПД наклонной плоскости падает.
Все задачи, поставленные перед исследованием, успешно выполнены.