п.1. Полезная работа и затраченная работа
Полезной называется работа по подъёму грузов или преодолению какого-либо сопротивления.
Затраченной (полной) называется работа, совершённая приложенной силой.
Примеры полной и полезной работы
Затраченная работа равна сумме:
- полезной работы;
- работы против силы трения в различных частях механизма;
- работы по перемещению различных составных элементов механизма.
Поэтому всегда (A_text{полезная}lt A_text{затраченная})
п.2. КПД механизма
Коэффициент полезного действия механизма – это отношение его полезной работы к затраченной работе. $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%} $$
Поскольку в реальных механизмах всегда (A_text{п}lt A_text{з}), $$ frac{A_text{п}}{A_text{з}}lt 1. $$
Следовательно КПД реальных механизмов (etalt 100text{%}).
Только в идеальном механизме, в котором нет потерь на трение, и все составные элементы не имеют веса, (A_text{п}=A_text{з}) и (eta=100text{%}).
КПД никогда не может быть выше (100text{%}).
КПД реальных механизмов можно увеличить за счет снижения трение в подвижных узлах и уменьшения веса всех составных элементов конструкции.
Для этого нужны новые смазочные вещества и лёгкие, но прочные конструкционные материалы.
п.3. Задачи
Задача 1. По наклонной плоскости поднимают груз массой 50 кг, прикладывая к нему силу 250 Н, направленную вдоль плоскости. Чему равен КПД плоскости, если её длина 10 м, а высота 3 м?
Дано:
(m=50 text{кг})
(gapprox 10 text{м/с}^2)
(F=250 text{Н})
(L=10 text{м})
(h=3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза begin{gather*} A_text{п}=mgh. end{gather*} Затраченная работа на перемещение груза вдоль наклонной плоскости begin{gather*} A_text{з}=FL. end{gather*} КПД плоскости: begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{FL}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{50cdot 10cdot 3}{250cdot 10}cdot 100text{%}=60text{%} end{gather*} Ответ: 60%
Задача 2. С помощью подвижного блока поднимают груз массой 200 кг, прикладывая силу 1200 Н. Чему равен КПД блока?
Дано:
(m=200 text{кг})
(gapprox 10 text{м/с}^2)
(F=1200 text{Н})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза и проигрыш в расстоянии. Т.е. при работе нужно вытянуть трос длиной (2h). Затраченная работа: begin{gather*} A_text{з}=Fcdot 2h. end{gather*} КПД блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{2Fh}cdot 100text{%}=frac{mg}{2F}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{200cdot 10}{2cdot 1200}cdot 100text{%}approx 83,3text{%} end{gather*} Ответ: 83,3%
Задача 3. Груз массой 245 кг с помощью рычага равномерно подняли на высоту 6 см. При этом к длинному плечу рычага была приложена сила 500 Н, а точка приложения силы опустилась на 30 см. Найдите КПД рычага.
Дано:
(m=245 text{кг})
(gapprox 10 text{м/с}^2)
(h_2=6 text{см}=0,6 text{м})
(F_1=500 text{Н})
(h_1=30 text{см}=0,3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию длинного плеча рычага: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД рычага begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{245cdot 10cdot 0,06}{500cdot 0,3}cdot 100text{%}=frac{147}{150}cdot 100text{%}=98text{%} end{gather*} Ответ: 98%
Задача 4. Чему равен КПД гидравлической машины, если для равномерного подъема груза массой 1,2 т к меньшему поршню прикладывают силу 160 Н? Площади поршней равны 5 см2 и 500 см2.
Дано:
(m=1,2 text{т}=1200 text{кг})
(gapprox 10 text{м/с}^2)
(F_1=160 text{Н})
(S_1=5 text{см}^2=5cdot 10^{-4} text{м}^2)
(S_2=500 text{см}^2=5cdot 10^{-2} text{м}^2)
__________________
(eta-?)
При опускании малого поршня на высоту (h_1) из малого в большой цилиндр вытекает объем жидкости равный $$ V=S_1h_1=S_2h_2Rightarrow frac{h_2}{h_1}=frac{S_1}{S_2} $$ Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию поршня малого цилиндра: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД гидравлической машины begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%}=frac{mgS_1}{F_1S_2}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{1200cdot 10cdot 5cdot 10^{-4}}{160cdot 5cdot 10^{-2}}cdot 100text{%}=frac{600}{800}cdot 100text{%}=75text{%} end{gather*} Ответ: 75%
Задача 5*. Груз массой 12 кг поднимают с помощью подвижного блока массой 3 кг. Чему равен КПД блока?
Дано:
(M=12 text{кг})
(m=3 text{кг})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза. Поэтому достаточно приложить силу, равную половине суммы весов груза и блока: begin{gather*} F=frac 12(M+m)g end{gather*} При этом будет проигрыш в расстоянии. Потребуется вытянуть трос длиной (2h). Затраченная работа, приложенная к тросу: begin{gather*} A_text{з}=Fcdot 2h=frac 12(M+m)gcdot 2h=(M+m)gh. end{gather*} КПД подвижного блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Mgh}{(M+m)gh}cdot 100text{%}=frac{M}{M+m}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{12}{12+3}cdot 100text{%}=80text{%} end{gather*} Ответ: 80%
Задача 6. Сколько воды можно поднять из колодца глубиной 36 м за 1 ч, если мощность электродвигателя равна 5 кВт, КПД всей установки равно 70%?
Дано:
(N=5 text{кВт}=5cdot 10^3 text{Вт})
(eta=70text{%}=0,7)
(h=36 text{м})
(t=1 text{ч}=3600 text{с})
(gapprox 10 text{м/с}^2)
__________________
(m-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Затраченная работа электродвигателя: begin{gather*} A_text{з}=Nt. end{gather*} КПД установки begin{gather*} eta=frac{A_text{п}}{A_text{з}}=frac{mgh}{Nt} end{gather*} Масса воды begin{gather*} m=frac{eta Nt}{gh} end{gather*} Получаем: begin{gather*} m=frac{0,7cdot 5cdot 10^3cdot 3600}{10cdot 36}=35cdot 10^3 (text{кг})=35 text{т} end{gather*} Ответ: 35 т
Задача 7*. КПД подвижного блока при подъеме первого груза равен 80%, а при подъеме второго груза – 90%. Масса какого груза больше и во сколько раз? Трением в блоке можно пренебречь.
Дано:
(eta_1=80text{%}=0,8)
(eta_2=90text{%}=0,9)
__________________
(frac{M_2}{M_1}-?)
КПД подвижного блока массой (m), с помощью которого поднимают груз массой (M) begin{gather*} eta=frac{M}{M+m} end{gather*} (см. Задачу 5 выше). Масса груза begin{gather*} eta(M+m)=MRightarrow eta m=(1-eta)MRightarrow M=frac{eta}{1-eta}m end{gather*} Получаем: begin{gather*} M_1=frac{0,8}{1-0,8}m=4m,\[6pt] M_2=frac{0,9}{1-0,9}m=9m end{gather*} Масса второго груза больше.
Отношение масс begin{gather*} frac{M_2}{M_1}=frac{9m}{4m}=2,25 (text{раз}) end{gather*} Ответ: масса второго груза больше в 2,25 раз
п.4. Лабораторная работа №13. Определение КПД наклонной плоскости
Цель работы
Научиться проводить измерения и рассчитывать КПД простого механизма на примере наклонной плоскости. Исследовать зависимость КПД наклонной плоскости от высоты.
Теоретические сведения
Работа по подъему тела весом (P) вертикально на высоту (h) (из точки C в точку B): $$ A_text{CB}=Ph $$
Работа по перемещению того же тела силой (F), направленной вдоль наклонной плоскости длиной (L) (из точки A в точку B): $$ A_text{AB}=FL $$
В обоих случаях тело перемещается с нулевого уровня AC, где (h_0=0), на уровень с высотой (h) в точку B. Работа сторонних сил в этом случае равна изменению потенциальной энергии тела: $$ A=A_text{CB}=A_text{AB}=Delta E_p $$
Получаем уравнение для идеальной наклонной плоскости (без трения): $$ Ph=FL $$
При наличии трения получаем неравенство: $$ Phlt FL $$
Полезная и затраченная работа для наклонной плоскости: $$ A_text{п}=Ph, A_text{з}=FL $$
КПД наклонной плоскости: $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Ph}{FL}cdot 100text{%} $$
Затраченная работа равна сумме полезной работы и работы по преодолению силы трения: $$ A_text{з}=A_text{п}+F_text{тр}L $$
Откуда сила трения равна: $$ F_text{тр}=frac{A_text{з}-A_text{п}}{L}=frac{FL-Ph}{L}=F-Pfrac hL $$
Вес (P) и сила (F) определяются в работе с помощью динамометра с ценой деления (d=0,1 text{Н}).
Абсолютная погрешность прямых измерений $$ Delta_F=Delta_P=frac d2=0,05 text{Н}. $$
Сила (F) определяется в серии из пяти опытов с вычислением средних величин.
Высота наклонной плоскости (h) и длина наклонной плоскости (L) определяются с помощью мерной ленты с ценой деления (d=5 text{мм}). Абсолютная погрешность (Delta_L=2,5 text{мм}).
Относительные погрешности измерений вычисляются как обычно.
Относительная погрешность расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L $$
Абсолютная погрешность расчета КПД: $$ Delta_eta=etacdot delta_eta $$
Приборы и материалы
Доска длиной от 70 см, штатив с муфтой и лапкой, брусок массой не менее 300 г, мерная лента, динамометр.
Ход работы
1. Измерьте мерной лентой длину доски (L).
2. Определите вес бруска (P) с помощью динамометра.
3. Соберите наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L3.)
4. Положите брусок на наклонную плоскость, прикрепите к нему динамометр и равномерно тяните по наклонной плоскости. Следите, чтобы динамометр располагался параллельно наклонной плоскости. Запишите измеренное значение (F). Повторите измерение (F) в серии из пяти опытов.
5. Соберите новую наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L4). Перейдите на шаг 4 и повторите серию опытов для определения (F).
6. Рассчитайте КПД для двух исследованных наклонных плоскостей. Найдите относительные и абсолютные погрешности расчетов КПД.
7. Для каждой из наклонных плоскостей укажите величину полезной и затраченной работы, найдите силу трения.
8. Сделайте выводы о зависимости силы трения и КПД от высоты наклонной плоскости.
Результаты измерений и вычислений
Длина наклонной плоскости (доски) begin{gather*} L=80 text{см}=800 text{мм},\[7pt] Delta_L=2,5 text{мм},\[6pt] delta_L=frac{Delta_L}{L}=frac{2,5}{800}approx 0,0031=0,31text{%} end{gather*}
Вес бруска begin{gather*} P=4,4 text{Н},\[7pt] Delta_P=0,05 text{Н},\[6pt] delta_P=frac{Delta_P}{P}=frac{0,05}{4,4}approx 0,0011=1,1text{%} end{gather*}
1. Наклонная плоскость высотой (h=27 text{см})
Высота наклонной плоскости begin{gather*} h=27 text{см}=270 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{270}approx 0,0093=0,93text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,9 | 2,8 | 3,0 | 2,7 | 2,8 | 14,2 |
| $$ Delta_F, H $$ | 0,06 | 0,04 | 0,16 | 0,14 | 0,04 | 0,44 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{14,2}{5}=2,84 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,44}{5}approx 0,09 (text{Н}),\[6pt] F=(2,84pm 0,09) text{Н},\[7pt] delta_F=frac{0,09}{2,84}approx 0,032=3,2text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,27=1,188 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,84cdot 0,8=2,272 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,84-4,4cdot frac{0,27}{0,8}approx 1,36 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{1,188}{2,272}approx 0,523=52,3text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,032+0,011+0,0093+0,0031=0,0554approx 0,056=5,6text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,523cdot 0,056approx 0,029=2,9text{%} $$
Окончательно получаем: $$ eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%} $$
2. Наклонная плоскость высотой (h=20 text{см})
Высота наклонной плоскости begin{gather*} h=20 text{см}=200 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{200}approx 0,013=1,3text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,4 | 2,6 | 2,5 | 2,6 | 2,5 | 12,6 |
| $$ Delta_F, H $$ | 0,12 | 0,08 | 0,02 | 0,08 | 0,02 | 0,32 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{12,6}{5}=2,52 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,32}{5}approx 0,06 (text{Н}),\[6pt] F=(2,52pm 0,06) text{Н},\[7pt] delta_F=frac{0,06}{2,52}approx 0,024=2,4text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,2=0,88 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,52cdot 0,8=2,016 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,52-4,4cdot frac{0,2}{0,8}approx 1,42 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{0,88}{2,016}approx 0,437=43,7text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,024+0,011+0,013+0,0031=0,0511approx 0,052=5,2text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,437cdot 0,052approx 0,023=2,3text{%} $$
Окончательно получаем: $$ eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%} $$
Выводы
На основании полученных результатов можно сделать следующие выводы.
В работе проводился расчет КПД наклонной плоскости постоянной длины, но разной высоты.
Для высоты около (h=frac L3):
- полезная и затраченная работы: (A_text{П}=1,188 (text{Дж}), A_text{З}=2,272 (text{Дж}))
- сила трения: (F_text{тр}=1,36 (text{Н}))
- КПД: (eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%})
Для высоты около (h=frac L4):
- полезная и затраченная работы: (A_text{П}=0,88 (text{Дж}), A_text{З}=2,016 (text{Дж}))
- сила трения: (F_text{тр}=1,42 (text{Н}))
- КПД: (eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%})
Таким образом, с уменьшением высоты:
- сила трения растет;
- КПД наклонной плоскости падает.
Все задачи, поставленные перед исследованием, успешно выполнены.
Задачи на КПД простых механизмов с решениями
Формулы, используемые на уроках «Задачи на КПД простых механизмов».
Название величины |
Обозначение |
Единица измерения |
Формула |
Сила |
F |
Н |
|
Полезная работа |
Ап |
Дж |
Ап = mgh1 |
Затраченая работа |
Аз |
Дж |
Аз = Fh2 |
КПД |
ɳ |
% |
ɳ = Ап / Аз * 100% |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Груз массой 3,6 кг равномерно переместили к вершине наклонной плоскости длиной 2,4 м и высотой 0,6 м. При этом была приложена сила 15 Н. Каков КПД установки?
Задача № 2.
Вычислите КПД рычага, с помощью которого груз массой 200 кг равномерно подняли на высоту 0,03 м, при этом к длинному плечу рычага была приложена сила 400 Н, а точка приложения силы опустилась на 0,2 м.
Задача № 3.
Груз массой 30 кг поднимают на высоту 12 м с помощью неподвижного блока, действуя на веревку силой 400 Н. Вычислите КПД установки.
Задача № 4.
Высота наклонной плоскости 1,2 м, а длина 12 м. Для подъема по ней груза весом 2000 Н потребовалась сила 250 Н. Определите КПД этой наклонной плоскости.
Задача № 5.
Груз массой 15 кг равномерно перемещают по наклонной плоскости, прикладывая при этом силу в 40 Н. Чему равно КПД наклонной плоскости, если длина ее 1,8 м, а высота — 30 см?
Краткая теория для решения задачи на КПД простых механизмов.
Конспект урока «Задачи на КПД простых механизмов с решениями».
Следующая тема: «».
В данном разделе вы уже познакомились с устройством и принципом работы двух простых механизмов: рычага и блока. Используя эти механизмы, мы совершаем какую-то работу.
До этого мы рассматривали идеализированные условия. Учитывали только следующие величины: приложенная к механизму сила, вес поднимаемого тела, плечи сил рычага.
Мы не учитывали ни силу трения между деталями механизмов, ни веса самого рычага, ни веса веревки в блоке, с помощью которой мы поднимаем груз. Если в лабораторных условиях эти величины могут показаться незначительными, то, например, вес каната в блоке подъемного крана уже сложно назвать незначительной величиной.
Следовательно, и работу таких механизмов тогда нужно рассчитывать по-другому. Для этого в физике разделяют работу на полную и полезную, вводят понятие коэффициента полезного действия (КПД) механизма. На данном уроке мы познакомимся с этими величинами и рассмотрим решение задач с использованием КПД.
Затраченная и полезная работы
Введем новые определения. Какую работу называют полезной, какую — полной?
Полная (затраченная) работа ($A_з$) — это работа, совершенная приложенной силой.
Полезная работа ($A_п$) — это работа по поднятию груза или преодолению какого-либо сопротивления.
В идеальных условиях (какие мы рассматривали в прошлых уроках) полная работа будет равна полезной. Но на практике между этими величинами есть разница.
На практике совершенная с помощью механизма полная работа всегда несколько больше полезной работы:
$A_п < A_з$, или $frac{A_п}{A_з} < 1$.
Почему при применении механизмов для подъема грузов и преодоления какого-либо сопротивления полезная работа не равна полной?
Например, при использовании подвижного блока (рисунок 1) мы будем дополнительно совершать работу по поднятию самого блока, веревки, ее креплений, а также по преодолению силы трения в оси блока.
КПД механизма
Что такое коэффициент полезного действия механизма?
Коэффициент полезного действия механизма (КПД) — это отношение полезной работы к полной работе:
$КПД = frac{A_п}{A_з}$.
КПД выражают в процентах и обозначают греческой буквой $eta$ (“эта”):
$eta = frac{A_п}{A_з} cdot 100%$.
Из этого определения следует, что КПД механизма всегда будет меньше $100%$.
Ученые и инженеры при конструировании механизмов всегда стремятся увеличить их КПД.
Как можно увеличить коэффициент полезного действия?
Первое, что для этого делают — стремятся уменьшить вес механизмов и трение в их осях.
В ходе истории и научно-технического прогресса коэффициент полезного действия механизмов постепенно возрастал:
- парового двигателя — $1−8%$;
- бензинового двигателя — $20−25%$;
- электрического двигателя — $90−95%$.
Как вы видите, на данный момент современные технологии обеспечивают достаточно высокий уровень КПД.
Примеры задач
Задача №1
Для поднятия груза массой $150 space кг$ используют рычаг. Груз подняли на высоту $h_1 = 0.15 space м$, приложив к длинному плечу рычага силу в $320 space Н$. При этом точка приложения этой силы опустилась на $h_2 =0.8 space м$. Рассчитайте коэффициент полезного действия рычага.
Дано:
$m = 150 space кг$
$h_1 = 0.15 space м$
$h_2 = 0.8 space м$
$F = 320 space Н$
$g = 9.8 frac{Н}{кг}$
$eta — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для нахождения КПД:
$eta = frac{A_п}{A_з} cdot 100%$.
Полная (затраченная) работа будет определяться приложенной силой:
$A_з = Fh_2 = 320 space Н cdot 0.8 space м = 256 space Дж$.
Полезная работа будет определяться работой по подъему груза весом $P = gm$ на высоту $h_1$:
$A_п = Ph_1 = gmh_1 = 9.8 frac{Н}{кг} cdot 150 space кг cdot 0.15 space м = 220.5 space Дж$.
Тогда:
$eta = frac{220.5 space Дж}{256 space Дж} cdot 100% approx 0.86 cdot 100% = 80%$.
Ответ: $eta = 80%$.
Задача №2
Используя неподвижный блок рабочий поднял груз массой $80 space кг$ на высоту $7 space м$ (рисунок 2). Найдите полную работу, совершенную рабочим, если КПД этого механизма $75%$.
Дано:
$m = 80 space кг$
$h = 7 space м$
$eta = 75%$
$g = 9.8 frac{Н}{кг}$
$A_з — ?$
Показать решение ответ
Скрыть
Решение:
Запишем формулу для нахождения КПД:
$eta = frac{A_п}{A_з} cdot 100%$.
Выразим из нее полную (затраченную) работу:
$A_з = frac{A_п cdot 100%}{eta}$.
Полезная работа — это работа по подъему груза:
$A_п = Ph = gmh = 9.8 frac{Н}{кг} cdot 80 space кг cdot 7 space м = 5488 space Дж$.
Найдем полную работу:
$A_з = frac{A_п}{eta} cdot 100%= frac{5488 space Дж}{75%} cdot 100%= frac{5488 space Дж}{0.75} approx 7300 space Дж = 7.3 space кДж$.
Ответ: $A_з = 7.3 space кДж$.

При перемещении тела с помощью простых механизмов (рычагов, блоков, наклонной плоскости) приложенной силе приходится преодолевать не только вес самого груза.
Например: Надо поднять груз с помощью подвижного блока на высоту. Для поднятия груза человек прикладывает к веревке силу (F тяги). Какую работу он при этом совершает? Надо поднять непосредственно груз весом Р. Кроме груза надо поднять еще веревку и блок весом Р бл. Надо преодолеть трение о воздух и в осях блока, мешающее подьему.
1. Какую работу называют полной? Полная ( или иначе затраченная) работа – это работа, совершенная приложенной силой, и равная работе по подъему груза и преодолению какого-либо сопротивления подъему.
Полную (затраченную) работу обычно обозначают — А.
1. Какую работу называют полезной? Полезная работа – это работа приложенной силы, совершенная для подъема непосредственно груза. Полезную работу обычно обозначают — Ап.
Совершаемая с помощью механизма полная работа всегда больше полезной работы.
Часть затрачиваемой работы расходуется на преодоление трения в оси механизма и сопротивления воздуха, а также на движение самого механизма. .
3. Что такое коэффициент полезного действия механизма? Отношение полезной работы к полной работе называется коэффициентом полезного действия. Сокращенно коэффициент полезного действия обозначается КПД.
КПД обычно выражают числом или в процентах и обозначают греческой буквой, которая читается как «эта».
4. Может ли КПД быть больше единицы? Полезная работа всегда меньше затраченной работы. Поэтому КПД любого механизма всегда меньше 100% ( или меньше 1).
Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их вес. 4. Пример решения задачи на расчет КПД. Задача. На коротком плече рычага подвешен груз массой 100 кг. Для его подъема к длинному плечу приложили силу 250 Н. Груз подняли на высоту h1 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h2 = 0,4 м.
Найти КПД рычага. Следующая страница – смотретьНазад в “Оглавление” – смотреть
Вся та энергия, которая потребляется механизмами, расходуется для того, чтобы преодолевать как полезные, так и вредные сопротивления.
Под полезными в технике подразумеваются те сопротивления, преодоление которых и является основным предназначением машины. Например, для металлообрабатывающих станков таковым является сопротивление резанию металла, в подъемных механизмах и машинах – масса поднимаемого груза и т.п.
Под вредными в технике подразумеваются те сопротивления, которые для своего преодоления требуют расходования энергии не дающей полезного эффекта. Таковыми являются, например, сила трения, возникающая при функционировании механизмов между их составными частями, а также сопротивление той среды, в которой происходит полезное движение.
Принято считать, что чем большую часть потребляемой энергии механизм затрачивает для того, чтобы преодолевать полезные сопротивления, тем более совершенным он является. Если выражать степень совершенства механизма математически, то можно использовать следующее соотношение:
где: η – коэффициент полезного действия (КПД); An – работа, которая расходуется машиной для того, чтобы преодолеть полезное сопротивление; Aз – работа движущих сил или та энергия, которая затрачивается (потребляется) машиной.
В большинстве случаев коэффициент полезного действия (КПД) выражают в процентах, и для этого для его вычисления используют следующую формулу:
Такой показатель, как коэффициент полезного действия, на практике применяется отнюдь не только для того, чтобы оценивать степень совершенства машин. КПД используют и для того, чтобы определять эффективность любых сложных механических устройств, а также тех приспособлений, которые не относятся к машинам, однако воспринимают, потребляют и отдают энергию. К таковым относятся, к примеру, топки паровых котлов (в них осуществляется преобразование энергии химической в энергию тепловую), электрических двигателей (в них электрическая энергия преобразуется в механическую), электрических осветительных приборов (в них электрическая энергия преобразовывается в световую) и т.п.
Когда возникает задача определения коэффициента полезного действия сложного по своей конструкции устройства, которое состоит из некоторого количества узлов, агрегатов и механизмов, потребляющих энергию, то наиболее целесообразно вычислять не только общий КПД, но и КПД всех отдельных составных частей.
В качестве примера можно рассмотреть установку, которая предназначается для освещения различных помещений и состоит из следующих частей: станция, вырабатывающая электроэнергию; электрические провода; лампы накаливания.
С практической точки зрения интересно выяснить не только то, какой именно коэффициент полезного действия имеет эта конструкция в целом, но и то, каков именно КПД двигателя, передающего вращение электрогенератору; самого электрогенератора; проводников электрической сети; ламп накаливания. Это позволяет, помимо всего прочего, определить наименее эффективные с точки зрения затрат энергии компоненты системы и, по возможности, использовать вместо них те, которые имеют более высокий КПД (например, светодиодные светильники вместо ламп накаливания).
Коэффициент полезного действия машины, механизма или любого другого устройства, отдельные части которого последовательно потребляют передаваемую от одного компонента к другому энергию, равняется произведению КПД этих компонентов. Что касается коэффициента полезного действия механизмов, то он всегда тем ниже, чем выше потери на трение.
Известно, что вечный двигатель невозможен. Это связано с тем, что для любого механизма справедливо утверждение: совершённая с помощью этого механизма полная работа (в том числе на нагревание механизма и окружающей среды, на преодоление силы трения) всегда больше полезной работы.
Например, больше половины работы двигателя внутреннего сгорания совершается впустую тратится на нагревание составных частей двигателя; некоторое количество теплоты уносят выхлопные газы.
Часто необходимо оценивать эффективность механизма, целесообразность его использования. Поэтому, чтобы рассчитывать, какая часть от совершённой работы тратится впустую и какая часть с пользой, вводится специальная физическая величина, которая показывает эффективность механизма.
Эта величина называется коэффициентом полезного действия механизма
Коэффициент полезного действия механизма равен отношению полезной работы к полной работе. Очевидно, коэффициент полезного действия всегда меньше единицы. Эту величину часто выражают в процентах.
Обычно её обозначают греческой буквой η (читается «эта»). Сокращённо коэффициент полезного действия записывают КПД.
η = (А_полн /А_полезн) * 100 %,где η КПД, А_полн полная работа, А_полезн полезная работа.
Среди двигателей наибольший коэффициент полезного действия имеет электрический двигатель (до 98 %). Коэффициент полезного действия двигателей внутреннего сгорания 20 % – 40 %, паровой турбины примерно 30 %. Отметим, что для увеличения коэффициента полезного действия механизма часто стараются уменьшить силу трения. Это можно сделать, используя различные смазки или шарикоподшипники, в которых трение скольжения заменяется трением качения.
[custom_ads_shortcode1]
Примеры расчета КПД
Рассмотрим пример. Велосипедист массой 55 кг поднялся на велосипеде массой 5 кг на холм, высота которого 10 м, совершив при этом работу 8 кДж. Найдите коэффициент полезного действия велосипеда. Трение качения колёс о дорогу не учитывайте.
Решение. Найдём общую массу велосипеда и велосипедиста:
None P = mg = 60 кг * 10 Н/кг = 600 ННайдём работу, совершённую на подъём велосипеда и велосипедиста:
None = А_полн /А_полезн * 100 % = 6 кДж / 8 кДж * 100 % = 75 %Ответ: КПД велосипеда равен 75 %.
Рассмотрим ещё один пример. На конец плеча рычага подвешено тело массой m. К другому плечу прилагают силу F, направленную вниз, и его конец опускается на h. Найдите, насколько поднялось тело, если коэффициент полезного действия рычага равен η %.
Решение. Найдём работу, совершённую силой F:
None Ответ: тело поднялось на высоту Fhη / 100 / mg.
[custom_ads_shortcode2]
Нужна помощь в учебе?
Предыдущая тема: Приложение закона равновесия рычага к блоку: золотое правило механики
Следующая тема: Энергия: потенциальная и кинетическая энергия
| Твитнуть | Нравится | Нравится |
Все неприличные комментарии будут удаляться.
Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу Aз и полезную работу Aп. Если, например, наша цель — поднять груз массой m на высоту h, то полезная работа — это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:
Aп = Fтh = mgh. (24.1)Если же мы применяем для подъема груза блок или какой-либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже), что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:
Aз > AпПолезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.
Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.
Сокращенное обозначение коэффициента полезного действия — КПД. Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма. Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой η (читается «эта»):
η =* 100% (24.2)Поскольку числитель Aп в этой формуле всегда меньше знаменателя Aз, то КПД всегда оказывается меньше 1 (или 100%).
Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их массу. В тех случаях, когда трение ничтожно мало и используемые механизмы имеют массу, пренебрежимо малую по сравнению с массой поднимаемого груза, коэффициент полезного действия оказывается лишь немного меньше 1. В этом случае затраченную работу можно считать примерно равной полезной работе:
Aз ≈ Aп (24.3)Следует помнить, что выигрыша в работе с помощью простого механизма получить нельзя.
Поскольку каждую из работ в равенстве (24.3) можно выразить в виде произведения соответствующей силы на пройденный путь, то это равенство можно переписать так: F1s1 ≈ F2s2 (24.4)Отсюда следует, что,выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот.
Этот закон называют «золотым правилом» механики. Его автором является древнегреческий ученый Герон Александрийский, живший в I в. н. э.
«Золотое правило» механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
Так, например, благодаря этому правилу мы сразу можем сказать, что рабочему, изображенному на рисунке 47, при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см.
1. Почему затраченная при использовании механизмов работа оказывается все время больше полезной работы? 2.
Что называют коэффициентом полезного действия механизма? 3. Может ли КПД механизма быть равным 1 (или 100%)?
Почему? 4. Каким образом увеличивают КПД?
5. В чем заключается «золотое правило» механики? Кто его автор?
6. Приведите примеры проявления «золотого правила» механики при использовании различных простых механизмов.
Источники:
- class-fizika.ru
- gk-drawing.ru
- www.nado5.ru
- phscs.ru
Методика расчета
-
Мощность,
затрачиваемая электродвигателем
механизма подъёма крана, определяется
по формуле
где
Gгр
– сила тяжести поднимаемого груза
(равна десятикратной массе груза,
выраженной в кг.) (Н)
Vпод
– скорость подъёма груза м/сек
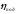
КПД механизма подъёма груза – 0,8
-
Мощность,
затрачиваемая электродвигателем
механизма передвижения крана, определяется
по формуле
где
Vпер
– скорость передвижения крана м/сек

КПД механизма передвижения крана

полное статистическое сопротивление,
определённое как сумма сопротивления
от сил трения Wтр
и от ветровой нагрузки Wв
(Н)
Сопротивление
сил трения Wтр
складывается
из следующих составляющих

сопротивления трения, возникающие при
качении колеса по рельсу Н
где
Gкр
– сила тяжести крана Н

коэффициент трения качения стального
колеса по рельсу

0,08;
Дп
–
диаметр ходового колеса – 60 см

сопротивление трения, возникающие в
ступице колёс
где
f
–
коэффициент трения в подшипниках ступицы
колеса = 0,02
d
–
диаметр ступицы колеса = 12см
Кр
–
коэффициент, учитывающий трения реборд
колёс о рельсы – 1,8
Wв
–
сила сопротивления ветра
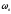
удельное сопротивление от лобового
ветра

30 Н/т
М-
масса крана
-
Определение
технической производительности крана

(m/час)
где
Тц
– время одного цикла крана

tз
–
время застропки груза с
tо
– время отстропки груза с
Н
–
средняя высота подъёма груза (м)

среднее расстояние перемещение крана
м

среднее расстояние перемещение тележки
м
Vгр
–
скорость подъёма груза м/c
Vпр
–скорость
перемещения крана м/с
Vт
–
скорость передвижения тележки м/с

коэффициент совмещения операций = 0,85
-
Определение
сменной эксплуатационной производительности
кран

где
Т –
число часов в смену
Квр
–
коэффициент использования машины по
времени.
Вопросы
91 по 100
Расчёт
площади склада для тарно-штучных грузов.
|
Варианты |
Годовой |
Коэффициент Кв |
Количество П |
Средняя |
||||
|
Повагонные Qг |
Мелкие Qг |
|||||||
|
Прибытие |
Отправление |
Прибытие |
Отправление |
|||||
|
Повагонные
q |
Мелкие |
|||||||
|
91 |
80 |
90 |
30 |
20 |
1.1: |
2 |
30 |
25 |
|
92 |
100 |
70 |
15 |
40 |
1.2 |
3 |
36 |
26 |
|
93 |
90 |
60 |
25 |
30 |
1.1 |
2 |
38 |
28 |
|
94 |
110 |
100 |
20 |
20 |
1.2 |
3 |
40 |
30 |
|
95 |
120 |
70 |
35 |
25 |
1.1 |
2 |
37 |
25 |
|
96 |
130 |
50 |
40 |
10 |
1.2 |
3 |
40 |
28 |
|
97 |
80 |
100 |
30 |
40 |
1.1 |
2 |
38 |
25 |
|
98 |
60 |
110 |
20 |
35 |
1.2 |
3 |
40 |
30 |
|
99 |
90 |
120 |
35 |
25 |
1.1 |
2 |
36 |
25 |
|
100 |
130 |
70 |
50 |
25 |
1.2 |
3 |
39 |
25 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #








![[eta =frac{A_{pol1}+A_{pol2}+dots +A_{poln}}{A}=frac{A_1{eta }_1+A_2{eta }_2+dots A_n{eta }_2}{A_1+A_2+dots A_n}left(6right)]](https://fizikinfo.ru/wp-content/uploads/2019/07/Koeffitsient-poleznogo-dejstvija-mehanizma1.png)









![[eta =frac{A_1}{W}cdot 100% ]](https://fizikinfo.ru/wp-content/uploads/2019/07/Koeffitsient-poleznogo-dejstvija-mehanizma12.png)


![[frac{{N-N}_{potr}}{N}=1-eta left(4right),]](https://fizikinfo.ru/wp-content/uploads/2019/07/Koeffitsient-poleznogo-dejstvija-mehanizma15.png)