Как найти кпд наклонной поверхности

Как найти кпд наклонной поверхности

п.1. Полезная работа и затраченная работа

Полезной называется работа по подъёму грузов или преодолению какого-либо сопротивления.
Затраченной (полной) называется работа, совершённая приложенной силой.

Примеры полной и полезной работы

Затраченная работа равна сумме:

  • полезной работы;
  • работы против силы трения в различных частях механизма;
  • работы по перемещению различных составных элементов механизма.

Поэтому всегда (A_text{полезная}lt A_text{затраченная})

п.2. КПД механизма

Коэффициент полезного действия механизма – это отношение его полезной работы к затраченной работе. $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%} $$

Поскольку в реальных механизмах всегда (A_text{п}lt A_text{з}), $$ frac{A_text{п}}{A_text{з}}lt 1. $$

Следовательно КПД реальных механизмов (etalt 100text{%}).

Только в идеальном механизме, в котором нет потерь на трение, и все составные элементы не имеют веса, (A_text{п}=A_text{з}) и (eta=100text{%}).

КПД никогда не может быть выше (100text{%}).

КПД реальных механизмов можно увеличить за счет снижения трение в подвижных узлах и уменьшения веса всех составных элементов конструкции.

Для этого нужны новые смазочные вещества и лёгкие, но прочные конструкционные материалы.

п.3. Задачи

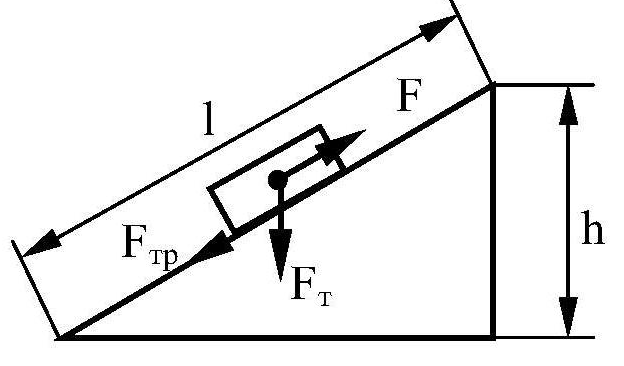
Задача 1. По наклонной плоскости поднимают груз массой 50 кг, прикладывая к нему силу 250 Н, направленную вдоль плоскости. Чему равен КПД плоскости, если её длина 10 м, а высота 3 м?

Дано:
(m=50 text{кг})
(gapprox 10 text{м/с}^2)
(F=250 text{Н})
(L=10 text{м})
(h=3 text{м})
__________________
(eta-?)

Полезная работа по подъему груза begin{gather*} A_text{п}=mgh. end{gather*} Затраченная работа на перемещение груза вдоль наклонной плоскости begin{gather*} A_text{з}=FL. end{gather*} КПД плоскости: begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{FL}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{50cdot 10cdot 3}{250cdot 10}cdot 100text{%}=60text{%} end{gather*} Ответ: 60%

Задача 2. С помощью подвижного блока поднимают груз массой 200 кг, прикладывая силу 1200 Н. Чему равен КПД блока?

Дано:
(m=200 text{кг})
(gapprox 10 text{м/с}^2)
(F=1200 text{Н})
__________________
(eta-?)

Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза и проигрыш в расстоянии. Т.е. при работе нужно вытянуть трос длиной (2h). Затраченная работа: begin{gather*} A_text{з}=Fcdot 2h. end{gather*} КПД блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{2Fh}cdot 100text{%}=frac{mg}{2F}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{200cdot 10}{2cdot 1200}cdot 100text{%}approx 83,3text{%} end{gather*} Ответ: 83,3%

Задача 3. Груз массой 245 кг с помощью рычага равномерно подняли на высоту 6 см. При этом к длинному плечу рычага была приложена сила 500 Н, а точка приложения силы опустилась на 30 см. Найдите КПД рычага.

Дано:
(m=245 text{кг})
(gapprox 10 text{м/с}^2)
(h_2=6 text{см}=0,6 text{м})
(F_1=500 text{Н})
(h_1=30 text{см}=0,3 text{м})
__________________
(eta-?)

Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию длинного плеча рычага: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД рычага begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{245cdot 10cdot 0,06}{500cdot 0,3}cdot 100text{%}=frac{147}{150}cdot 100text{%}=98text{%} end{gather*} Ответ: 98%

Задача 4. Чему равен КПД гидравлической машины, если для равномерного подъема груза массой 1,2 т к меньшему поршню прикладывают силу 160 Н? Площади поршней равны 5 см2 и 500 см2.

Дано:
(m=1,2 text{т}=1200 text{кг})
(gapprox 10 text{м/с}^2)
(F_1=160 text{Н})
(S_1=5 text{см}^2=5cdot 10^{-4} text{м}^2)
(S_2=500 text{см}^2=5cdot 10^{-2} text{м}^2)
__________________
(eta-?)

При опускании малого поршня на высоту (h_1) из малого в большой цилиндр вытекает объем жидкости равный $$ V=S_1h_1=S_2h_2Rightarrow frac{h_2}{h_1}=frac{S_1}{S_2} $$ Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию поршня малого цилиндра: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД гидравлической машины begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%}=frac{mgS_1}{F_1S_2}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{1200cdot 10cdot 5cdot 10^{-4}}{160cdot 5cdot 10^{-2}}cdot 100text{%}=frac{600}{800}cdot 100text{%}=75text{%} end{gather*} Ответ: 75%

Задача 5*. Груз массой 12 кг поднимают с помощью подвижного блока массой 3 кг. Чему равен КПД блока?

Дано:
(M=12 text{кг})
(m=3 text{кг})
__________________
(eta-?)

Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза. Поэтому достаточно приложить силу, равную половине суммы весов груза и блока: begin{gather*} F=frac 12(M+m)g end{gather*} При этом будет проигрыш в расстоянии. Потребуется вытянуть трос длиной (2h). Затраченная работа, приложенная к тросу: begin{gather*} A_text{з}=Fcdot 2h=frac 12(M+m)gcdot 2h=(M+m)gh. end{gather*} КПД подвижного блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Mgh}{(M+m)gh}cdot 100text{%}=frac{M}{M+m}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{12}{12+3}cdot 100text{%}=80text{%} end{gather*} Ответ: 80%

Задача 6. Сколько воды можно поднять из колодца глубиной 36 м за 1 ч, если мощность электродвигателя равна 5 кВт, КПД всей установки равно 70%?
Дано:
(N=5 text{кВт}=5cdot 10^3 text{Вт})
(eta=70text{%}=0,7)
(h=36 text{м})
(t=1 text{ч}=3600 text{с})
(gapprox 10 text{м/с}^2)
__________________
(m-?)

Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Затраченная работа электродвигателя: begin{gather*} A_text{з}=Nt. end{gather*} КПД установки begin{gather*} eta=frac{A_text{п}}{A_text{з}}=frac{mgh}{Nt} end{gather*} Масса воды begin{gather*} m=frac{eta Nt}{gh} end{gather*} Получаем: begin{gather*} m=frac{0,7cdot 5cdot 10^3cdot 3600}{10cdot 36}=35cdot 10^3 (text{кг})=35 text{т} end{gather*} Ответ: 35 т

Задача 7*. КПД подвижного блока при подъеме первого груза равен 80%, а при подъеме второго груза – 90%. Масса какого груза больше и во сколько раз? Трением в блоке можно пренебречь.
Дано:
(eta_1=80text{%}=0,8)
(eta_2=90text{%}=0,9)
__________________
(frac{M_2}{M_1}-?)

КПД подвижного блока массой (m), с помощью которого поднимают груз массой (M) begin{gather*} eta=frac{M}{M+m} end{gather*} (см. Задачу 5 выше). Масса груза begin{gather*} eta(M+m)=MRightarrow eta m=(1-eta)MRightarrow M=frac{eta}{1-eta}m end{gather*} Получаем: begin{gather*} M_1=frac{0,8}{1-0,8}m=4m,\[6pt] M_2=frac{0,9}{1-0,9}m=9m end{gather*} Масса второго груза больше.
Отношение масс begin{gather*} frac{M_2}{M_1}=frac{9m}{4m}=2,25 (text{раз}) end{gather*} Ответ: масса второго груза больше в 2,25 раз

п.4. Лабораторная работа №13. Определение КПД наклонной плоскости

Цель работы
Научиться проводить измерения и рассчитывать КПД простого механизма на примере наклонной плоскости. Исследовать зависимость КПД наклонной плоскости от высоты.

Теоретические сведения

Теоретические сведения
Работа по подъему тела весом (P) вертикально на высоту (h) (из точки C в точку B): $$ A_text{CB}=Ph $$

Работа по перемещению того же тела силой (F), направленной вдоль наклонной плоскости длиной (L) (из точки A в точку B): $$ A_text{AB}=FL $$

В обоих случаях тело перемещается с нулевого уровня AC, где (h_0=0), на уровень с высотой (h) в точку B. Работа сторонних сил в этом случае равна изменению потенциальной энергии тела: $$ A=A_text{CB}=A_text{AB}=Delta E_p $$

Получаем уравнение для идеальной наклонной плоскости (без трения): $$ Ph=FL $$

При наличии трения получаем неравенство: $$ Phlt FL $$

Полезная и затраченная работа для наклонной плоскости: $$ A_text{п}=Ph, A_text{з}=FL $$

КПД наклонной плоскости: $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Ph}{FL}cdot 100text{%} $$

Затраченная работа равна сумме полезной работы и работы по преодолению силы трения: $$ A_text{з}=A_text{п}+F_text{тр}L $$

Откуда сила трения равна: $$ F_text{тр}=frac{A_text{з}-A_text{п}}{L}=frac{FL-Ph}{L}=F-Pfrac hL $$

Вес (P) и сила (F) определяются в работе с помощью динамометра с ценой деления (d=0,1 text{Н}).

Абсолютная погрешность прямых измерений $$ Delta_F=Delta_P=frac d2=0,05 text{Н}. $$

Сила (F) определяется в серии из пяти опытов с вычислением средних величин.

Высота наклонной плоскости (h) и длина наклонной плоскости (L) определяются с помощью мерной ленты с ценой деления (d=5 text{мм}). Абсолютная погрешность (Delta_L=2,5 text{мм}).

Относительные погрешности измерений вычисляются как обычно.

Относительная погрешность расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L $$

Абсолютная погрешность расчета КПД: $$ Delta_eta=etacdot delta_eta $$

Приборы и материалы
Доска длиной от 70 см, штатив с муфтой и лапкой, брусок массой не менее 300 г, мерная лента, динамометр.

Ход работы
1. Измерьте мерной лентой длину доски (L).
2. Определите вес бруска (P) с помощью динамометра.
3. Соберите наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L3.)
4. Положите брусок на наклонную плоскость, прикрепите к нему динамометр и равномерно тяните по наклонной плоскости. Следите, чтобы динамометр располагался параллельно наклонной плоскости. Запишите измеренное значение (F). Повторите измерение (F) в серии из пяти опытов.
5. Соберите новую наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L4). Перейдите на шаг 4 и повторите серию опытов для определения (F).
6. Рассчитайте КПД для двух исследованных наклонных плоскостей. Найдите относительные и абсолютные погрешности расчетов КПД.
7. Для каждой из наклонных плоскостей укажите величину полезной и затраченной работы, найдите силу трения.
8. Сделайте выводы о зависимости силы трения и КПД от высоты наклонной плоскости.

Результаты измерений и вычислений

Длина наклонной плоскости (доски) begin{gather*} L=80 text{см}=800 text{мм},\[7pt] Delta_L=2,5 text{мм},\[6pt] delta_L=frac{Delta_L}{L}=frac{2,5}{800}approx 0,0031=0,31text{%} end{gather*}

Вес бруска begin{gather*} P=4,4 text{Н},\[7pt] Delta_P=0,05 text{Н},\[6pt] delta_P=frac{Delta_P}{P}=frac{0,05}{4,4}approx 0,0011=1,1text{%} end{gather*}

1. Наклонная плоскость высотой (h=27 text{см})

Высота наклонной плоскости begin{gather*} h=27 text{см}=270 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{270}approx 0,0093=0,93text{%} end{gather*}

Определение силы тяги (F) в серии опытов

№ опыта 1 2 3 4 5 Сумма
$$ F, H $$ 2,9 2,8 3,0 2,7 2,8 14,2
$$ Delta_F, H $$ 0,06 0,04 0,16 0,14 0,04 0,44

begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{14,2}{5}=2,84 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,44}{5}approx 0,09 (text{Н}),\[6pt] F=(2,84pm 0,09) text{Н},\[7pt] delta_F=frac{0,09}{2,84}approx 0,032=3,2text{%} end{gather*}

Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,27=1,188 (text{Дж}) $$

Затраченная работа: $$ A_text{З}=FL=2,84cdot 0,8=2,272 (text{Дж}) $$

Сила трения: $$ F_text{тр}=F-Pfrac hL=2,84-4,4cdot frac{0,27}{0,8}approx 1,36 (text{Н}) $$

КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{1,188}{2,272}approx 0,523=52,3text{%} $$

Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,032+0,011+0,0093+0,0031=0,0554approx 0,056=5,6text{%} $$

При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,523cdot 0,056approx 0,029=2,9text{%} $$

Окончательно получаем: $$ eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%} $$

2. Наклонная плоскость высотой (h=20 text{см})

Высота наклонной плоскости begin{gather*} h=20 text{см}=200 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{200}approx 0,013=1,3text{%} end{gather*}

Определение силы тяги (F) в серии опытов

№ опыта 1 2 3 4 5 Сумма
$$ F, H $$ 2,4 2,6 2,5 2,6 2,5 12,6
$$ Delta_F, H $$ 0,12 0,08 0,02 0,08 0,02 0,32

begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{12,6}{5}=2,52 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,32}{5}approx 0,06 (text{Н}),\[6pt] F=(2,52pm 0,06) text{Н},\[7pt] delta_F=frac{0,06}{2,52}approx 0,024=2,4text{%} end{gather*}

Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,2=0,88 (text{Дж}) $$

Затраченная работа: $$ A_text{З}=FL=2,52cdot 0,8=2,016 (text{Дж}) $$

Сила трения: $$ F_text{тр}=F-Pfrac hL=2,52-4,4cdot frac{0,2}{0,8}approx 1,42 (text{Н}) $$

КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{0,88}{2,016}approx 0,437=43,7text{%} $$

Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,024+0,011+0,013+0,0031=0,0511approx 0,052=5,2text{%} $$

При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,437cdot 0,052approx 0,023=2,3text{%} $$

Окончательно получаем: $$ eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%} $$

Выводы
На основании полученных результатов можно сделать следующие выводы.

В работе проводился расчет КПД наклонной плоскости постоянной длины, но разной высоты.

Для высоты около (h=frac L3):

  • полезная и затраченная работы: (A_text{П}=1,188 (text{Дж}), A_text{З}=2,272 (text{Дж}))
  • сила трения: (F_text{тр}=1,36 (text{Н}))
  • КПД: (eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%})

Для высоты около (h=frac L4):

  • полезная и затраченная работы: (A_text{П}=0,88 (text{Дж}), A_text{З}=2,016 (text{Дж}))
  • сила трения: (F_text{тр}=1,42 (text{Н}))
  • КПД: (eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%})

Таким образом, с уменьшением высоты:

  • сила трения растет;
  • КПД наклонной плоскости падает.

Все задачи, поставленные перед исследованием, успешно выполнены.

Источник

КПД плоскости, блока, рычага

В этой статье научимся определять КПД наклонной плоскости, блоков и рычагов.

КПД неподвижного блока равен отношению полезной работы к затраченной, высоту подъема можно сократить:

КПД плоскости, блока, рычага

Подвижный блок дает выигрыш в силе в два раза, поэтому для него

КПД плоскости, блока, рычага

КПД рычага равен, аналогично, отношению полезной работы к затраченной:

КПД плоскости, блока, рычага

рычаг

КПД наклонной плоскости равен:

КПД плоскости, блока, рычага

наклонная плоскость1

И по-прежнему это то же отношение полезной работы к затраченной.

Задача 1.

С помощью подвижного блока поднимают груз весом 400 Н на высоту 4 м, действуя на веревку с силой 220 Н. Чему равен КПД блока?

Так как блок по условию подвижный, то дает выигрыш в силе в 2 раза:

КПД плоскости, блока, рычага

Ответ: 91%.

Задача 2.

С помощью рычага груз массой 150 кг подняли на высоту 0,2 м. При этом к длинному плечу была приложена сила 600 Н, под действием которой конец этого плеча опустился на 0,6 м. Найдите КПД рычага.

КПД плоскости, блока, рычага

Ответ: 83 %

Задача 3.

С помощью рычага, КПД которого 80%, подняли груз массой 120 кг на высоту 40 см. На какое` расстояние опустилось длинное плечо рычага, если к нему была приложена сила 500 Н?

КПД рычага:
КПД плоскости, блока, рычага

Отсюда

КПД плоскости, блока, рычага
Ответ: 1,2 м.

Задача 4.

Определить КПД наклонной плоскости при подъеме тела, если учащийся с помощью динамометра и линейки получил такие результаты: вес тела 1,4 Н; высота плоскости 0,2 м; длина плоскости 0,56 м; сила, приложенная к телу, 1 Н.

КПД плоскости, блока, рычага
Ответ: 50%.

Задача 5.

 Бетонную плиту объемом 0,5 мКПД плоскости, блока, рычага поднимают из воды с помощью подвижного блока. Какую силу необходимо прикладывать, когда плиту поднимают в воде и над поверхностью воды?

Плотность бетона равна КПД плоскости, блока, рычага кг/мКПД плоскости, блока, рычага.

Найдем массу бетонной плиты: КПД плоскости, блока, рычага кг. Вес плиты 11 кН. Поэтому, если блок подвижный, то достаточно развивать силу 5,5 кН, чтобы поднять эту плиту на воздухе с помощью подвижного блока. В воде нам будет помогать сила Архимеда:

КПД плоскости, блока, рычага

Таким образом, в воде вес плиты станет меньше на 5000 Н и станет равен 6000 Н. Поэтому достаточно 3000 Н для подъема плиты в воде при помощи такого блока.

Ответ: 5,5 кН на воздухе, 3 кН в воде.

Задача 6.

По наклонной плоскости длиной 5 м и высотой 1,5 м поднимают равномерно груз массой 180 кг. Какую силу нужно приложить к грузу, если КПД плоскости 60%?

КПД наклонной плоскости равен:

КПД плоскости, блока, рычага

Откуда

КПД плоскости, блока, рычага

Ответ: 900 Н.

Задача 7.

Какую работу необходимо совершить для подъема гранитной плиты объемом 4 мКПД плоскости, блока, рычага на высоту 2 м с помощью механизма с КПД 60%?

Полезная работа равна

КПД плоскости, блока, рычага

КПД механизма равен:

КПД плоскости, блока, рычага

Полная работа тогда
КПД плоскости, блока, рычага

Ответ: 347 кДж.

Задача 8.

С помощью подвижного блока поднимают груз массой 75 кг на высоту 10 м. КПД равен 60%. Определить полезную работу и силу, необходимую для подъема груза.
КПД подвижного блока:
КПД плоскости, блока, рычага

Отсюда

КПД плоскости, блока, рычага

КПД плоскости, блока, рычага

Ответ: КПД плоскости, блока, рычагаДж, КПД плоскости, блока, рычага Н.

Источник

нужны формулы КПД,полезной,затраченной работы наклонной плоскости



Ученик

(202),
закрыт



15 лет назад

Q

Знаток

(335)


15 лет назад

КПД = работа полезная / работа затраченная *100% (n=(Aп/Аз)*100%)
работа полезная = масса * ускорение свободного падения * высоту подъема (Aп=F*h=m*g*h)
работа затраченная = сила с которой тянут * длину наклонной плоскости (Аз=F*l)

учись студент) кинематика это 8 или 9 класс, в учебниках есть это все.

Сонечка Ржавина

Ученик

(207)


3 года назад

КПД = работа полезная / работа затраченная *100% (n=(Aп/Аз) *100%)
работа полезная = масса * ускорение свободного падения * высоту подъема (Aп=F*h=m*g*h)
работа затраченная = сила с которой тянут * длину наклонной плоскости (Аз=F*l)

Источник
Предмет: Физика.
Класс: 7 класс.
Учебник: Перышкин, А. В. Физика. 7 кл. [Текст]
: учеб. для общеобразоват. учебн. заведений / А. В.
Перышкин, – М. : Дрофа, 2010. – 192 с.
Тема урока: Определение коэффициента
полезного действия наклонной плоскости.
Цель урока: Знакомство обучающихся с новой
физической величиной – коэффициентом полезного
действия механизма.
Задачи урока: Обучающие:

  • Дать определение КПД механизма.
  • Убедиться на опытах, что полезная работа,
    выполненная с помощью наклонной плоскости,
    меньше затраченной работы.
  • Определить КПД при подъеме тела по наклонной
    плоскости.
  • Выяснить, от чего зависит КПД при подъеме тела
    по наклонной плоскости.
  • Показать связь изученного материала с жизнью.

Развивающие:

  • Создать условия для развития личности учеников
    в процессе их деятельности.
  • Способствовать развитию практических навыков
    измерения силы с помощью динамометра, выполнения
    схемы эксперимента.
  • Продолжить формирование умения выделять
    главное, выдвигать гипотезу и проверять её на
    опыте.

Воспитательные:

  • Продолжить развитие коммуникативных навыков
    работы в команде (взаимоуважение, взаимопомощь и
    поддержка).
Планируемые результаты: Предметные: обучающиеся
научатся измерять характеристики  наклонной
плоскости, рассчитывать полезную и затраченную
работу, КПД простого механизма; выяснят, что
полезная работа всегда меньше затраченной и,
следовательно,  КПД меньше 100 % и не зависит от
веса поднимаемого тела, но его можно увеличить,
увеличивая угол наклона плоскости к горизонту.

Формируемые
УУД:

  • Личностные: установление учащимися связи
    между целью учебной деятельности и ее мотивом
    (смыслообразование).
  • Регулятивные:
    • Выработка способности к мобилизации сил и
      энергии.
    • Умение постановки учебной задачи на основе
      соотнесения известного и неизвестного
      материала, прогнозирования результата,
    • Составления плана и последовательности
      действий, оценивания и контроля полученного
      результата, корректировки плана и способов
      действия в случае расхождения эталона  и
      полученного результата.
  • Коммуникативные: умение слушать,
    участвовать в коллективном обсуждении проблемы,
    вступать в диалог, точно выражать свои мысли,
    владение монологической и диалогической формами
    речи в соответствии с нормами родного языка,
     интегрироваться в группу сверстников и
    строить продуктивное сотрудничество со
    сверстниками и взрослыми.
  • Познавательные:
    • Умение осознанно строить речевое высказывание
      в устной и письменной форме, структурировать
      знания.
    • Постановка и решение проблемы, выбор наиболее
      эффективных способов выхода из проблемной
      ситуации в зависимости от конкретных условий,
      создание алгоритмов деятельности при решении
      проблем поискового характера.
    • Формирование знаково-символических УУД.
    • Самостоятельное формулирование познавательной
      цели,  выдвижение гипотезы.
    • Рефлексия способов и условий действия, контроль
      и оценка процесса и результатов деятельности.
    • Выделение необходимой информации.
Тип урока: Урок отработки специальных
умений и навыков.
Форма урока: Исследовательская работа
обучающихся.
Оборудование:
  • Компьютер, проектор, экран.
  • Комплект приборов для выполнения лабораторной
    работы: направляющая рейка, динамометр,
    измерительная лента, брусок, груз массой 100 г,
    штатив с муфтой и лапкой (14 шт.).
Материалы к уроку
  • Инструкция по  охране  труда  при
    выполнении лабораторной работы  «Измерение
    КПД при подъеме тела по наклонной плоскости» (14
    шт.) (Приложение 1).
  • Технологическая карта выполнения лабораторной
    работы «Измерение КПД при подъеме тела по
    наклонной плоскости» (14 шт.) (Приложение
    2    ).
  • Технологическая карта урока (Приложение
    3    ).
Авторский медиапродукт:
  • Презентация «Определение коэффициента
    полезного действия наклонной плоскости»,
    выполненная в программе Microsoft PowerPoint 2010, состоит
    из 28 слайдов, включая титульный.
Программное обеспечение: MS Office 2010, KMPlayer или другая
программа, поддерживающая файлы с расширением swf.

Сценарий урока состоит из  семи этапов.

1. Организационный (2 мин.): Учитель
отмечает отсутствующих на уроке обучающихся,
напоминает присутствующим на уроке, что они
продолжают изучать простые механизмы и уже знают
их определение, виды, «Золотое правило» механики,
правило равновесия рычага, а сегодня ребята
могут познакомиться еще с одной характеристикой
простого механизма, но после того, как откроют
закрытое пазлами послание.

2. Актуализация знаний (8 мин.):
 Учитель выводит на экран слайд 2 презентации к
уроку «Определение коэффициента полезного
действия наклонной плоскости». Программа
составлена следующим образом: по щелчку мыши,
точно подведенной к номеру вопроса, раскрывается
слайд с самим вопросом, на нем размещается текст
вопроса. Проверить правильность ответа можно по
щелчку мыши. По управляющей кнопке можно
вернуться на слайд № 2. Щелчком мыши по полю
правильно отвеченного вопроса пазл убирается и
открывается часть послания. Выбирается
следующий вопрос и все повторяется. Интереснее
выбирать вопросы в произвольной
последовательности. После ответа на последний
вопрос на экране открывается послание ребятам:
«Скажи мне – и я забуду. Покажи мне – и я запомню.
Дай мне действовать самому –  и я научусь!».

3. Создание проблемной ситуации (4 мин.):
Учитель создает и предлагает обучающимся найти
выход из проблемной ситуации: рабочему
необходимо загрузить тяжелую бочку на корабль,
но чтобы это сделать, надо приложить очень
большую силу – силу, равную весу бочки. Такую
силу рабочий приложить не может. Ребята
предлагают применить наклонную плоскость. Учитель
выводит на экран слайд 3 презентации к уроку
«Определение коэффициента полезного действия
наклонной плоскости» (на  него вставлена
 flash-модель Единой коллекции ЦОР «Простые
механизмы. Наклонная плоскость»), раскрывает
сцену 5. задает вопрос: только ли на подъем
груза расходуется затраченная рабочим энергия?
Обучающиеся предполагают, что часть энергии
расходуется на преодоление силы трения. Учитель
выводит на экран слайд 4 презентации к уроку
«Определение коэффициента полезного действия
наклонной плоскости», (на  него вставлена 
flash-модель Единой коллекции ЦОР «Коэффициент
полезного действия механизма»), раскрывает сцену
3. Обсуждается вопрос о возможности разного
соотношения работы, совершенной механизмом, и
энергии, которая расходуется на преодоление силы
трения. Ученики выдвигают предположения о
существовании физической величины,
характеризующей эффективность простого
механизма.

4. Изучение нового материала (8 мин.):
Учитель демонстрирует подъем тела с помощью
наклонной плоскости, измеряет вес тела и силу
трения, высоту и длину наклонной плоскости.
Обучающиеся сравнивают вес тела с силой трения,
высоту наклонной плоскости с ее длиной, делают
вывод о выигрыше в силе и проигрыше в расстоянии
при использовании наклонной плоскости.
Учитель  выводит на экран слайды 5-6
презентации к уроку «Определение коэффициента
полезного действия наклонной плоскости», дает
характеристику КПД  простого механизма.
Обучающиеся выполняют чертеж наклонной
плоскости с обозначением ее длины, высоты,
записывают определение и расчетную формулу КПД
простого механизма.

5. Исследовательская практическая работа
(17 мин.):  Учитель организует обсуждение плана
исследования. Обучающиеся составляют план и
последовательность действий для определения КПД
наклонной плоскости:

  1. Измерить вес бруска (Р).
  2. Измерить высоту наклонной плоскости (h).
  3. Рассчитать полезную работу по формуле
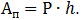
  4. Измерить силу трения (Fтр).
  5. Измерить длину наклонной плоскости (l).
  6. Рассчитать затраченную работу по формуле
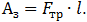
  7. Рассчитать КПД наклонной плоскости по
    формуле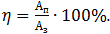 

Учитель выводит на экран слайды 7-11 презентации
к уроку «Определение коэффициента полезного
действия наклонной плоскости», проводит
инструктаж по безопасному выполнению
лабораторной работы, формулирует проблемный
вопрос: от каких параметров зависит КПД
наклонной плоскости. Обучающиеся
самостоятельно формулируют познавательную
задачу: проверить как зависит КПД наклонной
плоскости от веса поднимаемого тела и угла
наклонной плоскости? Выдвигают гипотезу: КПД
наклонной плоскости зависит от угла наклона и не
зависит от веса поднимаемого тела.

Учитель раздает ученикам комплекты приборов
для выполнения лабораторной работы, инструкцию
по  охране  труда  (Приложение
1), технологическую карту выполнения
лабораторной работы № 14  «Измерение
КПД при подъеме тела по наклонной плоскости» (Приложение 2),
 оказывает помощь группам обучающихся  в
выполнении работы. Обучающиеся выполняют
лабораторную работу при разном угле наклона
плоскости к горизонту и разном весе поднимаемого
груга.

6. Рефлексия (4 мин.): Обучающиеся
оценивают и анализируют полученные результаты
работы: Ап должна быть меньше Аз; высота
наклонной плоскости должна быть меньше ее длины,
полученный КПД должен быть меньше 100%. Если
полученный результат не верен, находят ошибку в
измерении или расчетах. Оформляют результаты
работы, делают вывод: в ходе лабораторной работы
КПД наклонной плоскости при угле наклона 20° к
горизонту оказался равным 45%, он всегда меньше
100%,  зависит от угла наклона (чем больше угол
наклона плоскости, тем больше ее КПД) и не зависит
от веса поднимаемого тела.

7. Домашнее задание (2 мин.): Учитель
выводит на экран слайд 12 презентации к уроку
«Определение коэффициента полезного действия
наклонной плоскости», озвучивает,
комментирует,  дает рекомендации по
эффективному выполнению домашнего задания:

  • § 61;
  • Подготовить сообщения (по желанию): 
  • Простые механизмы дома, на даче.
  • Простые механизмы в строительстве.
  • Простые механизмы и тело человека.

Адреса используемых ресурсов Интернет

  • http://files.school-collection.edu.ru/dlrstore/669b5266-e921-11dc-95ff-0800200c9a66/5_8.swf
  • http://files.school-collection.edu.ru/dlrstore/669b526a-e921-11dc-95ff-0800200c9a66/5_
    12.swf
Источник

Цель работы:
Убедиться на опыте в том, что полезная работа, выполненная с помощью простого механизма (наклонной плоскости), меньше полной.
Приборы и материалы:
Доска, динамометр, измерительная лента или линейка, брусок, штатив с муфтой и лапкой (рис. 206).
Указания к работе:
1. Повторите по учебнику § 65 “Коэффициент полезного действия механизма”.
2. Определите с помощью динамометра вес бруска.
3. Закрепите доску в лапке штатива в наклонном положении.
4. Положите брусок на доску, прикрепив к нему динамометр.
5. Перемещайте брусок с постоянной скоростью вверх по наклонной доске.
6. Измерьте с помощью линейки путь s, который проделал брусок, и высоту наклонной плоскости h.
7. Измерьте силу тяги F.
8. Вычислите полезную работу по формуле

А

п

=
P
h
, а затраченную − по формуле

А

з

=
F
s
.
9. Определите КПД наклонной плоскости:

η

=

А

п

А

з

.
10. Результаты измерений и вычислений занесите в таблицу 15.
Дополнительное задание.
1. Используя “золотое правило” механики, рассчитайте, какой выигрыш в силе даёт наклонная плоскость, если не учитывать трение.
2. Измените высоту наклонной плоскости и для неё определите полезную, полную работу и КПД.
Задание рисунок 1
рис. 206.
Таблица 15.
Задание рисунок 2

reshalka.com

ГДЗ учебник по физике 7 класс Перышкин. №11 Определение КПД при подъеме тела по наклонной плоскости. Номер №1

Решение

При выполнении данной работы необходимо вспомнить «золотое правило» механики. А именно, работа по равномерному перемещению тела по на­клонной плоскости без трения на высоту h равна ра­боте, совершенной при подъеме тела на высоту h по вертикали.
При подъеме по вертикали на высоту h, полезная работа равна:

А

п

=
m
g
h
.
При подъеме по плоскости работа равна:

А

з

=
F
s
, где F− сила, с которой груз поднимается равномерно, l — пройденный телом путь,

А

з

— затраченная работа.
В идеальном случае, когда нет силы трения,

А

п

=

А

з

.
Но поскольку при движении тела по плоскости возникает сила трения, то

А

п

<

А

з

.
Коэффициент полезного действия наклон­ной плоскости равен:

η

=

А

п

А

з

∗
100
.

Ход работы.
1. Определим с помощью динамометра вес бруска. Вес равен 2,2 Н.
2. Закрепим доску в лапке штатива в наклонном положении.
3. Положим брусок на доску, прикрепив к нему динамометр.
4. Переместим брусок с постоянной скоростью вверх по наклонной доске.
5. Измерим с помощью линейки путь s, который проделал брусок. Он равен 0,4 м. Измерим также высоту наклонной плоскости h, она равна 0,2 м.
6. Измерим силу тяги F. Сила тяги по показаниям динамометра равна 1,8 Н.
7. Вычислим полезную работу по формуле

А

п

=
P
h
, а затраченную − по формуле

А

з

=
F
s
.

А

п

=
2
,
2
∗
0
,
2
=
0
,
44
Дж;

А

з

=
1
,
8
∗
0
,
4
=
0
,
72
Дж.
8. Определим КПД наклонной плоскости:

η

=

А

п

А

з

∗
100
;

η

=

0
,
44

0
,
72

∗
100
%;
9. Результаты измерений и вычислений занесём в таблицу 15.

Таблица 15.

h, м Р, Н

А

п

, Дж

А

п

=
P
h

 s, м F, Н

А

з

, Дж

А

з

=
F
s

η

=

А

п

А

з

* 100%
0,2 2,2 0,44 0,4 1,8 0,72 61

Дополнительное задание.
1. В соответствии с “золотым правилом” механики:

А

п

=

А

з

;

Ph = Fs;

P
F

=

s
h

=

0
,
4

0
,
2

= 2.
Наклонная плоскость при отсутствии силы трения дала бы выигрыш в силе в 2 раза.
2. Изменим высоту наклонной плоскости и для неё определим полезную, полную работу и КПД.

А

п

=
2
,
2
∗
0
,
3
=
0
,
66
Дж;

А

з

=
1
,
9
∗
0
,
4
=
0
,
76
Дж;

η

=

0
,
66

0
,
76

∗
100
=
87
%;
3. Результаты измерений и вычислений занесём в таблицу.

h, м Р, Н

А

п

, Дж

А

п

=
P
h

 s, м F, Н

А

з

, Дж

А

з

=
F
s

η

=

А

п

А

з

* 100%
0,3 2,2 0,66 0,4 1,9 0,76 87

Решение рисунок 1

Источник

Добавить комментарий