Как найти кпд паровой турбины

Первые паровые двигатели не отличались универсальностью и эффективностью. Несовершенство конструкции приводило к высоким затратам на горючее при низком коэффициенте полезного действия.

В статье дан подробный разбор, что такое КПД паровых машин, от чего зависит этот параметр и как он рассчитывается. Дополнительно приведено сравнение КПД двигателей внешнего и внутреннего сгорания и примеры решения задач по расчетам КПД.

Каков средний коэффициент полезного действия?

КПД паровой машины зависит от степени выброса отработанного пара и конструктивных особенностей самой машины. В разные годы средняя характеристика машин постоянно увеличивалась:

1. Первые паровые машины Папена, Савери, Ньюкомена имели КПД 0,5-1%.

   У них была простая конструкция, которая не предусматривала конденсацию отработанного пара в отдельный котел.

2. Универсальная машина Уатта работала с КПД 8-25%. Она оснащалась 2 поршнями, золотниковым клапаном и конденсатором.
3. Тепловые электростанции с системой множественного расширения, конденсации, отсечкой работают с КПД 30-40%.
4. Современные парогазовые турбины работают с максимальным коэффициентом до 60 — 90%.

Стоит учесть, что рассматриваемая характеристика также зависит от общих габаритов устройства, в качестве привода какого устройства используются машины, и сколько процентов пара выводится в атмосферу.

Например, КПД тепловых станций, паровозов и пароходов увеличивается до 70-90 % в зимнее время, так как отработанный пар переводится в систему обогрева.

Каков КПД идеальной конструкции?

Идеальной паровой машиной считается двигатель, в котором температура подаваемого котлом пара, равна температуре используемого. При этом температура рабочего пара не должна снижаться за счет разницы с температурой внешней среды.

КПД идеальной паровой машины не может быть выше 50%. Данная характеристика рассчитывается по принципу Карно и его идеальной машины.

Также характеристика учитывает только работу с выпускаемым в атмосферу избытком отработанного пара. Если отработанный пар перенаправляется на работу иных механизмов или отопления, КПД повышается на 10-15%.

Почему устройства обладают невысоким параметром?

Причина кроется в технических особенностях каждого устройства и зависимости температуры пара в конденсаторе от внешней температуры среды. Разность температур называют температурным напором.

Для снижения зависимости применяется система из нескольких конденсаторов. Величина КПД зависит также от цикличности использования пара. Чем количество циклов больше, тем выше коэффициент полезной работы.

Какие способы используют для увеличения?

На величину КПД паровой машины влияют многие факторы. К ним можно отнести:

1. Производительность котла. Высокая производительность обеспечивает бесперебойное поступление пара без скачков температуры.
2. Компрессия цилиндров. Высокая компрессия позволяет использовать весь объем и давление впускного пара для смещения поршня.
3. Количество расширений. Множественное расширение (несколько цилиндров с увеличенным объемом) позволяют использовать пар в несколько циклов. Тем самым один объем пара доводится с высокого до низкого давления, осуществляя работу поршней.
4. Температура пара и цилиндров. Должна быть всегда высокой и стабильной. Если температура цилиндров ниже температуры пара, то часть энергии уходит на разогрев гильз, что снижает КПД.
5. Система распределения пара с отсечкой. Позволяет использовать только заданный объем пара. Система отсечки представляет собой впускной клапан. Он открывается на определенное время только для перемещения поршня.

   Как только пар с заданным давление впрыскивается в гильзу, клапан закрывается. Почему отсечка пара увеличивает показатель? Отсечка позволяет экономить общий объем пара и поддерживать стабильное давление в системе.

6. Система конденсации. Позволяет сохранять отработанный пар, конденсируя его в воду для повторного использования. Чем больше конденсаторов установлено на двигателе, тем выше температура отработанного пара и меньше объем конденсированной воды.

Еще одним фактором является применение использованного «мятого» пара. Если он переводится на работу вспомогательных систем, то КПД увеличивается, так как меньше пара выводится в атмосферу.

Как определить, чему равен показатель?

Рассмотрим, как рассчитать КПД парового двигателя.

Формула и алгоритм расчета

Коэффициент полезного действия для паровых двигателей определяет соотношение между выполненной механической работой и теплом, выделенным для производства пара. В физике данное значение обозначается буквой «n». Для расчета КПД паровой машины используется формула:

Формула состоит из следующих параметров:

• «η» — КПД машины.
• «W» — выполненная механическая работа (Дж).
• «Q» — объем затраченного тепла (Дж).

При расчете необходимо учитывать, что начальная температура пара всегда отличается от температуры используемого пара. При создании парового двигателя учитывается зависимость КПД от наличия конденсатора. Из этого следует, что начальная температура впрыска всегда выше температуры при конденсации.

Для его расчета применяется формула:

Выражение состоит из:

• «η» — КПД машины;
• «≤1» — отношение к циклу Карно. КПД парового двигателя всегда меньше 1 или 100%.
• «T2» — температура конечного цикла.
• «T1» — температура начального цикла.

Данная формула не применима для расчета КПД паровых машин без конденсатора и с прямым выводом отработанного пара в атмосферу. При расчете КПД паровых двигателей также учитывается масса сгораемого топлива и количество часов работы на этом топливе.

Несколько примеров

Далее будут даны 2 примера расчета величины КПД разных двигателей.

Задача:

1. Мощность паровой машины 220 кВт.
2. Получаемое для работы в течении 1 часа тепло 25,2 МДж.
3. КПД машины -?

Для расчета используется формула η= N/Q, где:

• «N» — мощность машины 220 кВт.
• «Q» — используемая теплота 25,2 МДж.
• Время работы 1 час или 3600 секунд.

Ответ: КПД парового двигателя мощностью 220 кВт равен 31,4%.

Задача:

1. Мощность парового двигателя 550 кВт.
2. Рабочее тепло 70,5 МДж.
3. Время работы 2 часа.
4. Отведенный пар используется в качестве отопления.
5. КПД -?

Ответ: КПД парового двигателя с последующим отводом на отопление равен 56,1%.

Что это означает: КПД равен 25 и 20%?

КПД 20 и 25% — это процентное соотношение полученной работы от использованной энергии. Иными словами, двигатель потребляет на работу всего 20-25% энергии пара от 100% сожженного горючего.

Остальные 80% уходят на:

• обогрев цилиндров,
• конденсацию,
• вывод в атмосферу,
• поддержание температуры и давления.

Сравнение с КПД бензинового двигателя

Прежде чем сравнивать два типа двигателей, необходимо учесть, что паровой двигатель -внешнего сгорания, а бензиновый — внутреннего. Также учитывается сложность конструкции и тип топлива.

Приведем сравнение:

1. КПД современных паровых машин может доходить до 60%, а турбин, работающих на ТЭЦ, до 90%.

   Но это параметры с учетом системы последующего использования пара в качестве отопления.

2. КПД бензиновых моторов зависит от качества сгораемого топлива и степени его воспламенения. Современные двигатели обладают КПД до 35%. Проблема заключается в потерях тепла на обогрев смежных механизмов и выбросах неотработанного топлива в атмосферу.
3. КПД дизельных двигателей достигает 55-60%. Этот тип мотора схож с паровым двигателем зависимостью от температуры рабочих цилиндров. При поддержании рабочей температуры топливо сгорает эффективнее, а значит без потери КПД.

При сравнении также стоит учитывать давление на вал и механическую работу иных механизмов.

Паровой двигатель не нуждается в установке коробки передач, раздаточной коробке и дифференциала. Отсюда следует, что вся полученная энергия тратится только на работу вала или махового колеса.

Заключение

Паровые машины способны показывать максимальную эффективность только при идеальной конструкции с учетом поддержания давления и температуры пара. Если эти критерии не соблюдаются, двигатель теряет значительную часть полезной работы.

При всей своей простоте, паровые двигатели остаются востребованными в энергетике, транспорте и производстве.

Кпд
турбины.
Потери тепловой энергии внутри паровой
турбины оцениваются относительным
внутренним кпд турбины,
который представляет собой отношение
использованного теплоперепада H_i
к
располагаемому теплоперепаду в турбине
Н₀,т.
е.

η_0i=H_i/H₀=(i₀-i_к)/(i₀-i_к.а), (3.30)

где
i₀
— энтальпия пара при начальных параметрах
пара, кДж/к i_к.а
— энтальпия пара при адиабатном
расширении пара от начального его
состояния до конечного, кДж/кг; i_к
— энтальпия пара при конечных параметрах
пара, кДж/кг. Значения относительного
внутреннего кпд паровых турбин находятся
в пределах 0,7…0,88.

Потери
теплоты на трение в подшипниках и на
привод вспомогательных механизмов
(механические потери) оценивают
механическим
кпд η_м,
который
представляет собой отношение эффективной
мощности N_e
к
внутренней N_i,
т.
е.

η_м=N_e/N_i. (3.31)

Значения
механического кпд турбин находятся в
пределах 0,97…0,99.

Потери
теплоты внутри турбины и механические
потери оцениваются относительным
эффективным кпд турбины,
который равен произведению относительного
внутреннего кпд турбины на механический
кпд, т. е.

η_о.е=η_оiη_м. (3.32)

Значения
η_о.е
турбин в зависимости от их мощности
находят в пределах 6,68…0,87.

Если
паровая турбина непосредственно
присоединена к электрическому генератору,
то электрическая мощность будет меньше
эффективной вследствие потерь в
генераторе, которые оцениваются кпд
генератора η_г.
Кпд электрического генератора представляет
собой отношение электрической мощности
N_э
к
эффективной N_e,
т.
e.

η_г=N_э/N_е. (3.33)

Значения кпд
генератора находятся в пределах
0,96…0,99.

Относительный
электрический кпд турбогенератора

η_о.э=η_о.еη_г=η_оiη_мη_г
(3.34)

Коэффициент
возврата теплоты турбины.
Коэффициент возврата теплоты α
характеризует относительное увеличение
располагаемого теплоперепада за счет
частичного возврата тепловых потерь и
определяется по формуле

; (3.35)

где
Σh₀
— сумма располагаемых во всех ступенях
турбины теплоперепадов, кДж/кг.

Коэффициент
возврата теплоты турбины при равенстве
от­носительных внутренних кпд отдельных
ступеней находится по формуле

(3.36)

Значения
коэффициента возврата теплоты турбины
в зависимости от числа ступеней находятся
в пределах 0,04…0,06.

Характеристический
коэффициент турбины.
Характеристический коэффициент турбины
Y[кг·м²/(кДж·с²)],
подобно отноше­нию и/с₁
для
ступеней, характеризует экономичность
турбины и в целом и определяется по
формуле

, (3.37)

где z
– количество
ступеней турбины; и_ср
—
средняя окружная скорость на середине
лопатки, м/с.

Мощности
турбины.
Эффективной
мощностью N_e
(кВт)
называют мощность, снимаемую с вала или
соединительной муфты турбины:

N_e=DH₀η_oe. (3.38)

Эффективная
мощность N_e
меньше
внутренней (индикатор­ной) мощности
N_i
на
величину мощности механических потерь
N_м,
т. е.

N_e=N_i–N_м. (3.39)

Внутренняя
(индикаторная)
мощность
N_i
(кВт)
находится из формулы (3.31).

Электрическая
мощность N_э
(кВт)
определяется из формулы (3.33).

Расход
пара турбины.
Экономичность паровой турбины оценивается
как кпд, так и удельным расходом пара.

Удельный
эффективный расход пара [кг/(кВт·ч)]
представляет собой отношение секундного
расхода пара D
к
эффективной мощности N_e,
т.
е.

d_e=D/N_e=3600/(η_oeН₀). (3.40)

Удельный
эффективный расход пара мощных
конденсационных турбин при полной
нагрузке составляет 3…4 кг/(кВтч).

Расход пара (кг/с)
на турбину с отбором пара находится по
формуле

, (3.41)

где
D_п
— отбор пара, кг/с; i₀
—
энтальпия пара при начальных параметрах
пара, кДж/кг; i_п
— энтальпия пара, поступающего из
отбора, кДж/кг; i_к
—
энтальпия пара в конденсаторе, кДж/кг.

Энтальпия пара,
поступающего из отбора:

i_п=i₀–(i₀–i_п.а)η, (3.42)

где
i_п.а
— энтальпия пара при адиабатном
расширении пара от начального состояния
до давления, при котором обеспечивается
отбор, кДж/кг;
η
—
относительный внутренний кпд части
высокого давления (до отбора).

Энтальпия пара в
конденсаторе

i_к=i_п–(i_п–i_к.а)η, (3.43)

где
i_к.а
—
энтальпия пара при адиабатном расширении
пара от давления отбора до давления в
конденсаторе, кДж/кг; η
– относительный
внутренний кпд части низкого давления
(после отбора).

Давление
и расход пара в ступенях турбины при
переменном режиме. Изменение
расхода пара через турбину вызывает
перераспределение давлений и теплоперепадов
в ее ступенях. Зависимость между расходом
и давлением пара в ступенях турбины для
скоростей пара в соплах ниже критических
выражается уравнением

, (3.44)

где
D₀
и
D
—
расходы пара через турбину соответственно
расчетном и рассматриваемом режимах,
кг/с; р₀
и
р₀₁
—
давления пара перед соплами первой или
любой ступени соответственно при
расчетном
и рассматриваемом режимах, Па; р₂
и
р₀₂
—
давления пара за рабочими лопатками
последней или любой ступени соответственно
при расчетном и рассматриваемом режимах,
Па. Изменение давления в ступени
конденсационной турбины в зависимости
от расхода пара

p₀₁=р₀D/D₀. (3.45)

Изменение
давления в ступени турбины с противодавлением
в зависимости от расхода пара

. (3.46)

Задача
3.49. Определить
относительный внутренний и эффективный
кпд турбины, если параметры пара перед
турбиной р₀=3,4
МПа,
t₀=440°C,
за турбиной р₂=0,4
МПа,
t₂=220°C
и
механический кпд турбины η_м=0,98.

Ответ:
η_oi=0,77;
η_o.e=0,755.

Задача
3.50.
Определить
относительный электрический кпд
турбогенератора, если параметры пара
перед турбиной р₀=4
МПа,
t₀=
390°C,
за турбиной р₂=1
МПа, t₂=240°С,
механический кпд турбины η_м=0,97
и кпд электрического генератора η_г=0,95.

Ответ:
η_оэ
= 0,71.

Задача
3.51.
При испытании турбины были измерены
параметры пара перед турбиной р₀=3,5
МПа, t₀=410°C
и за турбиной p₂=1,2
МПа и t₂=290°C.
Определить
коэффициент возврата теплоты, если
турбина имеет семь ступеней с одинаковыми
относительными внутренними кпд η=0,73.

Ответ:
α=0,057.

Задача
3.52.
Для турбины с начальными параметрами
пара р₀=0
МПа,
t₀=500°С
и противодавлением р₂=1,5
МПа определить коэффициент возврата
теплоты, если использованный теплопорепад
регулирующей ступени h=
102
кДж/кг и относительный внутренний кпд
регулирующей ступени η=0,68.
Турбина имеет шесть нерегулируемых
ступеней с одинаковыми располагаемыми
теплоперепадами h₀=62
кДж/кг.

Ответ:
α=0,053.

Задача
3.53.
Конденсационная турбина работает с
начальными параметрами пара р₀=9
МПа,
t₀=500°С
и давлением пара в конденсаторе р_к=4·10³
Па. Определить характеристический
коэффициент турбины, если коэффициент
возврата теплоты α=0,05
и средняя окружная скорость на середине
лопатки и_ср=220
м/с. Турбина имеет десять ступеней.

Ответ:
Y=334
кг·м²/(кДж·с²).

Задача
3.54.
Турбина работает с начальными параметрами
пара р₀=4
МПа,
t₀=440°C
и давлением пара в конденсаторе р_к=4·10³
Па. Определить эффективную мощность
турбины, если расход пара D=5,2
кг/с
и относительный эффективный кпд турбины
η_ос=0,71.

Ответ:
N_e=4560
кВт.

Задача
3.55. Турбина
работает с начальными параметрами пара
р₀=8
МПа, t₀=480°С
и давлением пара в конденсаторе р_к=3,5·10³
Па. Определить внутреннюю (индикаторную)
мощности турбины и мощность механических
потерь, если расход паpа
D=5,4
кг/с, относительный эффективный кпд
турбины η_ое=0,73
и механический кпд турбины η_м=0,97.

Ответ:
N_i=5527
кВт; N_м=166
кВт.

Задача
3.56.
Турбина работает с начальными параметрами
пара р₀=3,5
МПа, t₀=435°С
и давлением пара в конденсаторе
р_к=4·10³.
Определить
эффективную мощность турбины и удельный
эффективный расход пара, если расход
пара
D=5
кг/с и относительный эффективный кпд
турбины η_ое=0,72.

Решение:
Располагаемый теплоперепад Н₀=i₀–i_к.а
находим,
пользуясь is-диаграммой
(рис. 3.12). Энтальпия пара при заданных
начальных параметрах р₀
и
t₀
составляет
i₀=3315кДж/кг,
а энтальпия пара после адиабатного
расширения пара до р_к=4·10³
Па составляет i_к.а=2095
кДж/кг.

Н₀=i₀–i_к.а=3315-2095=1220
кДж/кг.

Эффективная
мощность турбины по формуле (3.38),

N_e=DH₀η_ое=5·1220·0,72=4392
кВт.

Удельный
эффективный расход пара, по формуле
(3.40),

d_e=3600/(η_oeН₀)=3600/(0,72·1220)=4,1
кг/(кВт·ч).

Задача
3.57. Турбина
с начальными параметрами пара р₀=1,6
МПа, t₀=350°C
и давлением пара в конденсаторе р_к=5·10³
Па переведена на работу при давлении в
конденсаторе р=9·10³
Па. На сколько уменьшится эффективная
мощность турбины, если при одном и том
же расходе пара (D=5,5
кг/с) относительный эффективный кпд
уменьшится с η_ое=0,66
до η_ое=
0,61.

Ответ:
ΔN_e
=489 кВт.

Задача
3.58. Турбина,
работающая с начальными параметрами
пара р₀=2,6
МПа, t₀=360°C
при
давлении пара в конденсаторе р_к=4,5·10³
Па, имеет относительный эффективный
кпд η_ое=0,68.
На сколько увеличится удельный эффективный
расход пара, если давление в конденсаторе
повысится до р=8·10³
Па, а относительный эффективный кпд
понизится до η_ое=0,63.

Ответ:
Δd_e=0,14
кг/(кВт·ч).

Задача
3.59. Конденсационная
турбина эффективной мощностью N_e=12000
кВт работает при начальных параметрах
р₀=2,8
МПа, t₀=400°C
и давлении пара в конденсаторе р_к=4,5·10³
Па. Определить удельный эффективный
расход пара и относительный эффективный
кпд турбины, если расход пара D=15
кг/с.

Ответ:
d_e=4,5
кг/(кВт·ч); η_ое=0,708.

Задача
3.60. Конденсационная
турбина работает при начальных параметрах
пара р₀=3,5
МПа,
t₀=435°С
и давлении пара в конденсаторе р_к=4·10³
Па. Определить секундный и удельный
расходы пара на турбину, если электрическая
мощность турбогенератора N_е=24000
кВт, относительный эффективный кпд
турбины η_ое=0,76
и кпд электрического генератора η_г=0,96.

Ответ:
D=21,7
кг/с;
d_e=3,9
кг/(кВт·ч).

Задача
3.61.
Турбина с регулируемым производственным
от­бором пара, работающая при начальных
параметрах пара р₀=3,5
МПа, t₀=435°С
и давлении пара в конденсаторе р_к=4·10³
Па, обеспечивает отбор пара D_n=5
кг/с
при давлении р_п=0,2
МПа. Определить расход пара на турбину,
если электрическая мощность турбогенератора
N_э=4000
кВт, относитель­ный внутренний кпд
части высокого давления (до отбора)
η=0,74,
относительный внутренний кпд части
низкого давления (после отбора) η=0,76,
механический кпд η_м=0,98
и кпд элект­рического генератора
η_г=0,96.

Решение:
Энтальпию пара i₀
при
заданных начальных параметрах пара р₀
и
t₀
находим
по is-диаграмме
(рис. 3.13): i₀=3315
кДж/кг. Энтальпии пара i_па
и i_ка,
получаемые при адиабатном расширении
от состояния р₀,
t₀
до
р_п
и
от р_п,
i_n
до
р_к,
находим, построив процесс адиабатного
расширения пара на
is-диаграмме
(рис. 3.13): i_па=2640
кДж/кг; i_ка=2240
кДж/кг.

Энтальпию
пара, поступающего из отбора, определяем
по формуле (3.42):

i_п=i₀-(i₀–i_па)η=3315-(3315-2640)0,74=2815
кДж/кг.

Энтальпия пара в
конденсаторе, по формуле (3.43),

i_к=i_п-(i_п–i_ка)η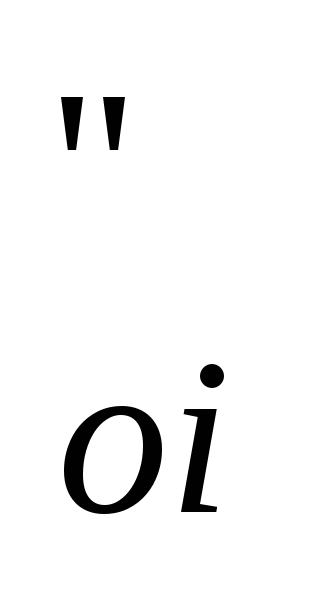=2815-(2815-2240)0,76=2378
кДж/кг.

Расход пара на
турбину, по формуле (3.41),

D=6,87
кг/с.

Задача
3.62. Турбина
с регулируе­мым производственным
отбором, ра­ботающая при начальных
параметрах пара р₀=3,5
МПа,
t₀=435°С
и давле­нии пара в конденсаторе
р_к=5·10³
Па, обеспечивает отбор пара D_n=11,1
кг/с при давлении р_п=0,5
МПа.
Определить удельный эффективный расход
пара, если элект­рическая мощность
турбогенератора N_э=6000
кВт, относительный внутренний кпд части
высокого давления (до отбора) η=0,78,
относительный внутренний кпд части
низкого давления (после отбора) η=0,65,
механический кпд η_м=0,98
и кпд электрического генератора η_г=0,95.

Ответ:
d_e=7,12
кг/(кВтч).

Задача
3.63. Турбина
с производственным отбором пара
работающая при начальных параметрах
пара р₀=3,5
МПа,
t₀=350°С
и давлении пара в конденсаторе р_к=4·10³
Па обеспечивает отбор пара D_п=4
кг/с
при давлении р_п=0,4
МПа.
Определить электрическую мощность
турбогенератора, если расход пара на
турбину D=8
кг/с, относительный внутренний кпд части
высокого давления (до отбора) η=0,75,
относительный в внутренний кпд части
низкого давления (после отбора) η=0,77,
механический кпд η_м=0,97
и кпд электрического генератора η_г=0,97.

Решение:
Энтальпию пара i₀
находим
по is-диаграмме
( 3.14): i₀=3110
кДж/кг. Энтальпии пара i_па
и i_ка
находим,
построив на is-диаграмме
(рис.3.14) процесс адиабатного расширения
пара от начального его состояния до
конечного, т. е.

i_па=2645
кДж/кг; i_ка=2095
кДж/кг.

Энтальпию
пара, поступающего из отбора, определяем
формуле (3.42):

i_п=i₀-(i₀–i_па)η=3110-(3110-2645)0,75=2761
кДж/кг.

Энтальпия
пара в конденсаторе, по формуле (3.43),

i_к=i_п-(i_п–i_ка)η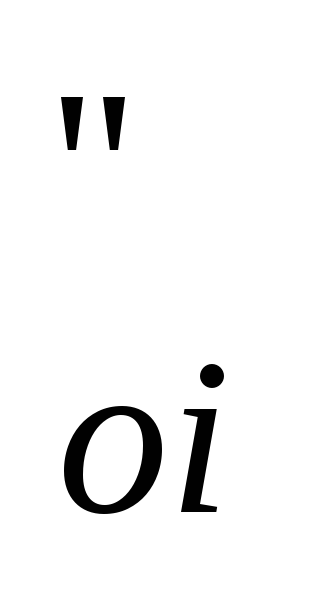=2761-(2761-2095)0,77=2248
кДж/кг.

Электрическая
мощность турбины, по формуле (3.41),

N_э=[D(i₀-i_к)-D_n(i_n-i_к)]η_мη_г=
=[8(3110-2248)-4(2761-2248)0,97·0,97=4553
кВт.

Задача
3.64. Турбина
с производственным отбором пара,
работающая при начальных параметрах
пара р₀=3,5
МПа,
t₀=350°С
и давлении пара в конденсаторе р_к=5·10³
Па, обеспечивает отбор пара D_п=5
кг/с при давлении р_п=0,4
МПа.
Определить эффективную мощность турбины,
если расход пара на турбину D=10
кг/с, относительный внутренний кпд части
высокого давления (до отбора) η=0,75,
относительный внутренний кпд части
низкого давления (после отбора) η=0,78
и механический кпд η_м=0,98.

Ответ:
N_e=5792
кВт.

Задача
3.65.
Конденсационная турбина, работающая
при на­чальных параметрах пара
р₀=3
МПа,
t₀=380°C
и
давлении пара в конденсаторе р_к=4·10³
Па, имеет один промежуточный отбор пара
при давлении р_п=0,4
МПа. Определить секундный и удель­ный
эффективный расходы пара на турбину,
если электрическая мощность турбогенератора
N_э=2500
кВт, относительный внутренний кпд части
высокого давления (до отбора) η=0,74,
относительный внутренний кпд части
низкого давления (после отбора) η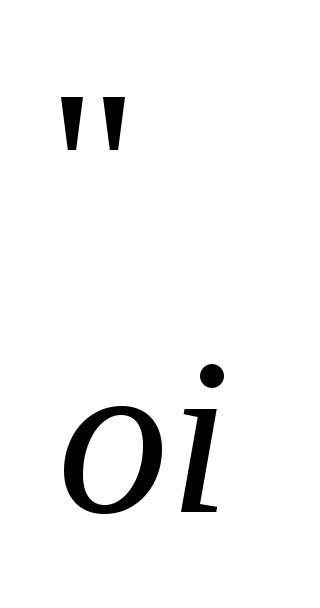=0,16,
механический
кпд турбины η_м=0,97,
кпд электрического генератора η_г=0,97
и доля расхода пара, отбираемого из
промежуточного отбора на производство,
α_п=D_п/D=0,5.

Решение:
Энтальпию пара i₀
находим
по is-диаграмме
(рис. 3.15): i₀=3190
кДж/кг.

Энтальпии
пара i_па
и i_ка
находим, построив процесс адиабатного
расширения пара на is-диаграмме
от начального его состояния до конечного:
i_па=2720
кДж/кг,
i_ка=2145
кДж/кг.

Энтальпию
пара, поступающего из отбора, определяем
по формуле (3.42):

i_п=i₀-(i₀–i_па)η=3190-(3190-2720)0,74=2842
кДж/кг.

Энтальпию
пара в конденсаторе находим по (3.43):

i_к=i_п-(i_п–i_ка)η=2842-(2842-2145)0,76=2312
кДж/кг.

Эффективная
мощность турбины, по формуле (3.33),

N_e=N_э/η_г=2500/0,97
= 2577 кВт.

Расход
пара на турбину, по формуле (3.41),

D=N_э/[(i₀-i_к)–α_n(i_n-i_к)]η_мη_г=2500/[(3190-2312)-0,5(2842-2312)]0,97·0,97=4,34
кг/с.

Удельный
расход пара на турбину, по формуле
(3.40),

d_е=D/N_e=4,34·3600/2577=6,06
кг/(кВт·ч).

Задача
3.66.
Конденсационная Турбина, работающая
при начальных параметрах пара р₀=3
МПа, t₀=380°С
и давлении пара в конденсаторе р_к=3·10³
Па, имеет один промежуточный отбор пара
давлении р₀=0,5
МПа. Определить эффективную мощность
турбины, если расход пара D=4,65
кг/с, относительный внутренний кпд части
высокого давления (до отбора) η=0,73,
относительный внутренний кпд части
низкого давления (после отбора) η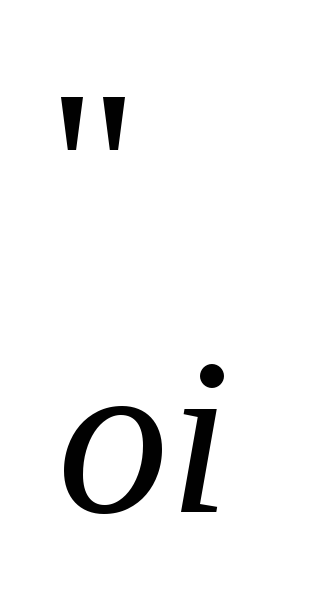=0,75,
механический кпд турбины η_м=0,96,
кпд электрического генератора η_г=0,97
и доля расхода пара, отбираемая из
промежуточного отбора на производство,
α_п=0,5.

Ответ:
N_e=2700
кВт.

Задача
3.67. Турбина
высокого давления с теплофикационным
отбором при давлении р_п=0,14
МПа работает при начальных параметрах
пара р₀=8
МПа, t₀=500°C
и имеет на одном из режимов работы
относительный внутренний кпд части
высокого давления η=0,8.
При изменении пропуска пара через
турбину при постоянном давлении отбора
относительный внутренний кпд части
высокого давления уменьшился до η=0,74.
На сколько
изменился
располагаемый теплоперепад части
низкого давления, если давление пара в
конденсаторе осталось постоянным и
равным р_к=6·10³
Па?

Ответ:
ΔН=10
кДж/кг.

Задача
3.68.
Определить
давление пара перед соплами первой
ступени при половинном пропуске пара
для турбины с противодавлением малой
мощности, выполненной с дроссельным
парораспределением, если давление пара
перед соплами первой ступени при полном
пропуске пара р₀=1,5
МПа и противодавление р₂=0,3
МПа.

Ответ:
р₀₁=0,794
МПа.

Задача
3.69. Определить
давление пара перед соплами регулирующей
ступени для турбины с противодавлением
при расходе пара D=82
кг/с, если при расходе пара D₀=102кг/с
давление пара перед соплами регулирующей
ступени р₀=7
МПа и противодавление р₂=3
МПа. Давление за турбиной неизменно.

Ответ:
р₀₁=6,45
МПа.

Задача
3.70. Конденсационная
турбина с начальным давлением пара
р₀=2,9
МПа
и расчетным расходом пара D₀=28
кг/с выполнена с дроссельным
парораспределением. Определить расход
пара через перегрузочный клапан, если
после его открытия общий расход увеличился
до D₁=32,2
кг/с. Давление пара за перегрузочным
клапаном в момент его открытия р₁=2
МПа. Перегрузка турбины осуществляется
обводным клапаном.

Решение:
Давление пара в перегрузочной камере
турбины определяем по формуле (3.45):

р₁₁=р₁D₁/D₀=2·32,2/28=2,3
МПа.

Так
как проходные площади в обведенной
группе ступеней не меняются и при данных
соотношениях давлений в этих ступенях
не возникает критическая скорость, то
расход пара через обведенную группу
ступеней находим по формуле (3.44):

=20
кг/с.

Расход пара через
перегрузочный клапан

D_n=D₁-D=32,2-20=12,2
кг/с.

In general, the thermal efficiency, η_th, of any heat engine is defined as the ratio of the work it does, W, to the heat input at the high temperature, Q_H.

The thermal efficiency, η_th, represents the fraction of heat, Q_H, that is converted to work. Since energy is conserved according to the first law of thermodynamics and energy cannot be converted to work completely, the heat input, Q_H, must equal the work done, W, plus the heat that must be dissipated as waste heat Q_C into the environment. Therefore we can rewrite the formula for thermal efficiency as:

This is a very useful formula, but here we express the thermal efficiency using the first law in terms of enthalpy.

Typically most nuclear power plants operate multi-stage condensing steam turbines. In these turbines, the high-pressure stage receives steam (this steam is nearly saturated steam – x = 0.995 – point C at the figure; 6 MPa; 275.6°C) from a steam generator and exhausts it to moisture separator-reheater (point D). The steam must be reheated to avoid damages caused to the steam turbine blades by low-quality steam. The reheater heats the steam (point D), and then the steam is directed to the low-pressure stage of the steam turbine, where it expands (point E to F). The exhausted steam then condenses in the condenser. It is at a pressure well below atmospheric (absolute pressure of 0.008 MPa) and is in a partially condensed state (point F), typically of a quality near 90%.

In this case, steam generators, steam turbine, condensers, and feedwater pumps constitute a heat engine that is subject to the efficiency limitations imposed by the second law of thermodynamics. In an ideal case (no friction, reversible processes, perfect design), this heat engine would have a Carnot efficiency of

= 1 – T_cold/T_hot = 1 – 315/549 = 42.6%

where the temperature of the hot reservoir is 275.6°C (548.7K), the temperature of the cold reservoir is 41.5°C (314.7K). But the nuclear power plant is the real heat engine, in which thermodynamic processes are somehow irreversible. They are not done infinitely slowly. In real devices (such as turbines, pumps, and compressors), mechanical friction and heat losses cause further efficiency losses.

To calculate the thermal efficiency of the simplest Rankine cycle (without reheating), engineers use the first law of thermodynamics in terms of enthalpy rather than in terms of internal energy.

The first law in terms of enthalpy is:

dH = dQ + Vdp

In this equation, the term Vdp is a flow process work. This work,  Vdp, is used for open flow systems like a turbine or a pump in which there is a “dp”, i.e., change in pressure. There are no changes in the control volume. As can be seen, this form of the law simplifies the description of energy transfer. At constant pressure, the enthalpy change equals the energy transferred from the environment through heating:

Isobaric process (Vdp = 0):

dH = dQ     →     Q = H₂ – H₁

At constant entropy, i.e., in isentropic process, the enthalpy change equals the flow process work done on or by the system:

Isentropic process (dQ = 0):

dH = Vdp     →     W = H₂ – H₁

Obviously, it will be very useful in the analysis of both thermodynamic cycles used in power engineering, i.e., in the Brayton and Rankine cycles.

The enthalpy can be made into an intensive or specific variable by dividing by the mass. Engineers use the specific enthalpy in thermodynamic analysis more than the enthalpy itself, and it is tabulated in the steam tables along with specific volume and specific internal energy. The thermal efficiency of such a simple Rankine cycle and in terms of specific enthalpies would be:

It is a very simple equation, and for the determination of the thermal efficiency, you can use data from steam tables.

Thermal Efficiency of Steam Turbine

In modern nuclear power plants, the overall thermal efficiency is about one-third (33%), so 3000 MWth of thermal power from the fission reaction is needed to generate 1000 MWe of electrical power. The reason lies in relatively low steam temperature (6 MPa; 275.6°C). Higher efficiencies can be attained by increasing the temperature of the steam. But this requires an increase in pressures inside boilers or steam generators. However, metallurgical considerations place upper limits on such pressures. Compared to other energy sources, the thermal efficiency of 33% is not much. But it must be noted that nuclear power plants are much more complex than fossil fuel power plants, and it is much easier to burn fossil fuel than to generate energy from nuclear fuel. Sub-critical fossil fuel power plants operated under critical pressure (i.e., lower than 22.1 MPa) can achieve 36–40% efficiency.

Causes of Inefficiency

As was discussed, an efficiency can range between 0 and 1. Each heat engine is somehow inefficient. This inefficiency can be attributed to three causes.

• Irreversibility of Processes. There is an overall theoretical upper limit to the efficiency of conversion of heat to work in any heat engine. This upper limit is called the Carnot efficiency. According to the Carnot principle, no engine can be more efficient than a reversible engine (Carnot heat engine) operating between the same high temperature and low-temperature reservoirs. For example, when the hot reservoir has T_hot of 400°C (673K) and T_cold of about 20°C (293K), the maximum (ideal) efficiency will be: = 1 – T_cold/T_hot = 1 – 293/673 = 56%. But all real thermodynamic processes are somehow irreversible, and they are not done infinitely slowly. Therefore, heat engines must have lower efficiencies than limits on their efficiency due to the inherent irreversibility of the heat engine cycle they use.
• Presence of Friction and Heat Losses. In real thermodynamic systems or real heat engines, a part of the overall cycle inefficiency is due to the losses by the individual components. In real devices (such as turbines, pumps, and compressors), mechanical friction, heat losses, and losses in the combustion process cause further efficiency losses.
• Design Inefficiency. Finally, the last and important source of inefficiencies is the compromises made by engineers when designing a heat engine (e.g., power plant). They must consider cost and other factors in the design and operation of the cycle. As an example, consider the design of the condenser in the thermal power plants. Ideally, the steam exhausted into the condenser would have no subcooling. But real condensers are designed to subcool the liquid by a few degrees of Celsius to avoid the suction cavitation in the condensate pumps. But, this subcooling increases the inefficiency of the cycle because more energy is needed to reheat the water.

Thermal Efficiency Improvement – Steam Turbine

There are several methods, how can be the thermal efficiency of the Rankine cycle improved. Assuming that the maximum temperature is limited by the pressure inside the reactor pressure vessel, these methods are:

Boiler and Condenser Pressures

As in the Carnot, Otto, and Brayton cycle, the thermal efficiency tends to increase as the average temperature at which energy is added by heat transfer increases and/or the average temperature at which energy is rejected decreases. This is the common feature of all thermodynamic cycles.

Condenser Pressure

The case of the decrease in the average temperature at which energy is rejected requires a decrease in the pressure inside the condenser (i.e., the decrease in the saturation temperature). The lowest feasible condenser pressure is the saturation pressure corresponding to the ambient temperature (i.e., the absolute pressure of 0.008 MPa, which corresponds to 41.5°C). The goal of maintaining the lowest practical turbine exhaust pressure is a primary reason for including the condenser in a thermal power plant. The condenser provides a vacuum that maximizes the energy extracted from the steam, resulting in a significant increase in network and thermal efficiency. But also this parameter (condenser pressure) has its engineering limits:

• Decreasing the turbine exhaust pressure decreases the vapor quality (or dryness fraction). At some point, the expansion must be ended to avoid damages that could be caused to blades of steam turbine by low-quality steam.
• Decreasing the turbine exhaust pressure significantly increases the specific volume of exhausted steam, which requires huge blades in the last rows of a low-pressure stage of the steam turbine.

In typical wet steam turbines, the exhausted steam condenses in the condenser, and it is at a pressure well below atmospheric (absolute pressure of 0.008 MPa, which corresponds to 41.5°C). This steam is in a partially condensed state (point F), typically of a quality near 90%. Note that there is always a temperature difference between (around ΔT = 14°C) the condenser temperature and the ambient temperature, which originates from the finite size and efficiency of condensers.

Boiler Pressure

The case of the increase in the average temperature at which energy is added by heat transfer requires either superheating of steam produced or an increase in the pressure in the boiler (steam generator). Superheating is not typical for nuclear power plants.

Typically most nuclear power plants operate multi-stage condensing steam turbines. In these turbines, the high-pressure stage receives steam (this steam is nearly saturated steam – x = 0.995 – point C at the figure; 6 MPa; 275.6°C). Since neither the steam generator is 100% efficient, there is always a temperature difference between the saturation temperature (secondary side) and the temperature of the primary coolant.

In a typical pressurized water reactor, the hot primary coolant (water 330°C; 626°F) is pumped into the steam generator through the primary inlet. This requires maintaining very high pressures to keep the water liquid. To prevent boiling of the primary coolant and provide a subcooling margin (the difference between the pressurizer temperature and the highest temperature in the reactor core), pressures around 16 MPa are typical for PWRs. The reactor pressure vessel is the key component that limits the thermal efficiency of each nuclear power plant since the reactor vessel must withstand high pressures.

Superheat and Reheat

As for the Carnot cycle, the thermal efficiency tends to increase as the average temperature at which energy is added by heat transfer increases. This is the common feature of all thermodynamic cycles.

One possible way is to superheat or reheat the working steam. Both processes are very similar in their manner:

• Superheater – increases the steam temperature above the saturation temperature
• Reheater – removes the moisture and increases steam temperature after a partial expansion.

The superheating process is the only way to increase the peak temperature of the Rankine cycle (and to increase efficiency) without increasing the boiler pressure. This requires the addition of another type of heat exchanger called a superheater, which produces the superheated steam.

Superheated vapor or superheated steam is a vapor at a temperature higher than its boiling point at the absolute pressure where the temperature is measured.

Reheat allows delivering more of the heat at a temperature close to the peak of the cycle. This requires the addition of another type of heat exchanger called a reheater. The use of the reheater involves splitting the turbine, i.e., using a multi-stage turbine with a reheater. It was observed that more than two stages of reheating are unnecessary since the next stage increases the cycle efficiency only half as much as the preceding stage.

The high pressure and low-pressure stages of the turbine are usually on the same shaft to drive a common generator, but they have separate cases. The flow is extracted with a reheater after a partial expansion (point D), run back through the heat exchanger to heat it back up to the peak temperature (point E), and then passed to the low-pressure turbine. The expansion is then completed in the low-pressure turbine from point E to point F.

In the superheater, further heating at fixed pressure increases both temperature and specific volume. The process of superheating water vapor in the T-s diagram is provided in the figure between state E and the saturation vapor curve. As can also be seen, wet steam turbines (e.g., used in nuclear power plants) use superheated steam, especially at the inlet of low-pressure stages. Typically most nuclear power plants operate multi-stage condensing wet steam turbines (the high-pressure stage runs on saturated steam). In these turbines, the high-pressure stage receives steam (this steam is nearly saturated steam – x = 0.995 – point C at the figure) from a steam generator and exhausts it to a moisture separator-reheater (point D). The steam must be reheated or superheated to avoid damages that could be caused to the blades of the steam turbine by low-quality steam. High content of water droplets can cause rapid impingement and erosion of the blades, which occurs when condensed water is blasted onto the blades. To prevent this, condensate drains are installed in the steam piping leading to the turbine. The reheater heats the steam (point D), and then the steam is directed to the low-pressure stage of the steam turbine, where it expands (point E to F). The exhausted steam is at a pressure well below atmospheric, and, as can be seen from the picture, the steam is in a partially condensed state (point F), typically of a quality near 90%. Still, it is much higher vapor quality than it would be without reheat. Accordingly, superheating also tends to alleviate the problem of low vapor quality at the turbine exhaust.

Since the temperature of the primary coolant is limited by the pressure inside the reactor, superheaters (except a moisture separator reheater) are not used in nuclear power plants, and they usually operate a single wet steam turbine.

Heat Regeneration

Significant increases in the thermal efficiency of steam turbine power plants can be achieved by reducing the amount of fuel that must be added to the boiler. This can be done by transferring heat (partially expanded steam) from certain steam turbine sections, which is normally well above the ambient temperature, to the feedwater. This process is known as heat regeneration, and a variety of heat regenerators can be used for this purpose. Sometimes engineers use the term economizer, which is a heat exchanger intended to reduce energy consumption, especially in preheating a fluid.

As can be seen in the article “Steam Generator”, the feedwater (secondary circuit) at the inlet of the steam generator may have about ~230°C (446°F) and then is heated to the boiling point of that fluid (280°C; 536°F; 6,5MPa) and evaporated. But the condensate at the condenser outlet may have about 40°C, so the heat regeneration in typical PWR is significant and very important:

• Heat regeneration increases the thermal efficiency since more of the heat flow into the cycle occurs at a higher temperature.
• Heat regeneration causes a decrease in the mass flow rate through a low-pressure stage of the steam turbine, thus increasing LP Isentropic Turbine Efficiency. Note that the steam has a very high specific volume at the last stage of expansion.
• Heat regeneration causes an increase in working steam quality since the drains are situated at the periphery of the turbine casing, where is a higher concentration of water droplets.

Regeneration vs. Recuperation of Heat

In general, the heat exchangers used in regeneration may be classified as either regenerators or recuperators.

• A regenerator is a heat exchanger where heat from the hot fluid is intermittently stored in a thermal storage medium before it is transferred to the cold fluid. It has a single flow path where the hot and cold fluids alternately pass through.

• A recuperator is a heat exchanger with separate flow paths for each fluid along its own passages, and heat is transferred through the separating walls. Recuperators (e.g., economizers) are often used in power engineering to increase the overall efficiency of thermodynamic cycles, for example, in a gas turbine engine. The recuperator transfers some of the waste heat in the exhaust to the compressed air, thus preheating it before entering the combustion chamber. Many recuperators are designed as counterflow heat exchangers.

Supercritical Rankine Cycle

As was discussed, the thermal efficiency can be improved “simply” by increasing the temperature of the steam entering the turbine. But this temperature is restricted by metallurgical limitations imposed by the materials and design of the reactor pressure vessel and primary piping. The reactor vessel and the primary piping must withstand high pressures and great stresses at elevated temperatures. But currently, improved materials and fabrication methods have permitted significant increases in the maximum pressures, with corresponding increases in thermal efficiency. The thermal power plants are currently designed to operate on the supercritical Rankine cycle (i.e., steam pressures exceeding the critical pressure of water 22.1 MPa, and turbine inlet temperatures exceeding 600 °C). Supercritical fossil fuel power plants that are operated at supercritical pressure have efficiencies of around 43%. Most efficient and complex coal-fired power plants operate at “ultra critical” pressures (i.e., around 30 MPa) and use multiple stage reheat to reach about 48% efficiency.

Supercritical Water Reactor – SCWR

The supercritical Rankine cycle is also the thermodynamic cycle of supercritical water reactors. The supercritical water reactor (SCWR) is a concept of Generation IV reactor that is operated at supercritical pressure (i.e., greater than 22.1 MPa). The term supercritical in this context refers to the thermodynamic critical point of water (T_CR = 374 °C;  p_CR = 22.1 MPa) and must not be confused with the criticality of the reactor core, which describes changes in the neutron population in the reactor core.

For SCWRs, a once-through steam cycle has been envisaged, omitting any coolant recirculation inside the reactor. It is similar to boiling water reactors, steam will be supplied directly to the steam turbine, and the feed water from the steam cycle will be supplied back to the core.

As well as, the supercritical water reactor may use light water or heavy water as a neutron moderator. As can be seen, there are many SCWR designs, but all SCWRs have a key feature, which is the use of water beyond the thermodynamic critical point as primary coolant. Since this feature allows to increase the peak temperature, the supercritical water reactors are considered a promising advancement for nuclear power plants because of their high thermal efficiency (~45 % vs. ~33 % for current LWRs).

Isentropic Efficiency – Turbine, Pump

In previous chapters, we assumed that the steam expansion is isentropic, and therefore we used T_4,is  as the outlet temperature of the gas. These assumptions are only applicable with ideal cycles.

Most steady-flow devices (turbines, compressors, nozzles) operate under adiabatic conditions, but they are not truly isentropic but are rather idealized as isentropic for calculation purposes. We define parameters η_T,  η_P, η_N, as a ratio of real work done by the device to work by the device when operated under isentropic conditions (in the case of the turbine). This ratio is known as the Isentropic Turbine/Pump/Nozzle Efficiency. These parameters describe how efficiently a turbine, compressor, or nozzle approximates a corresponding isentropic device. This parameter reduces the overall efficiency and work output. For turbines, the value of η_T is typically 0.7 to 0.9 (70–90%).

See also: Isentropic Process.

Steam Turbine – Problem with Solution

Let us assume the Rankine cycle, one of the most common thermodynamic cycles in thermal power plants. In this case, assume a simple cycle without reheat and without condensing steam turbine running on saturated steam (dry steam). In this case, the turbine operates at a steady state with inlet conditions of  6 MPa, t = 275.6°C, x = 1 (point 3). Steam leaves this turbine stage at a pressure of 0.008 MPa, 41.5°C, and x = ??? (point 4).

Calculate:

1. the vapor quality of the outlet steam
2. the enthalpy difference between these two states (3 → 4) corresponds to the work done by the steam, W_T.
3. the enthalpy difference between these two states (1 → 2) corresponds to the work done by pumps, W_P.
4. the enthalpy difference between these two states (2 → 3) corresponds to the net heat added to the steam generator
5. the thermodynamic efficiency of this cycle and compare this value with Carnot’s efficiency

1)

Since we do not know the same vapor quality of the outlet steam, we must determine this parameter. State 4 is fixed by the pressure p₄ =  0.008 MPa and the fact that the specific entropy is constant for the isentropic expansion (s₃ = s₄ = 5.89 kJ/kgK for 6 MPa). The specific entropy of saturated liquid water (x=0) and dry steam (x=1) can be picked from steam tables. In the case of wet steam, the actual entropy can be calculated with the vapor quality, x, and the specific entropies of saturated liquid water and dry steam:

s₄ = s_v x + (1 – x ) s_l              

where

s₄ = entropy of wet steam (J/kg K) = 5.89 kJ/kgK

s_v = entropy of “dry” steam (J/kg K) = 8.227 kJ/kgK (for 0.008 MPa)

s_l = entropy of saturated liquid water (J/kg K) = 0.592 kJ/kgK (for 0.008 MPa)

From this equation the vapor quality is:

x₄ =  (s₄ – s_l) / (s_v – s_l) = (5.89 – 0.592) / (8.227 – 0.592) = 0.694 = 69.4%

2)

The enthalpy for the state 3 can be picked directly from steam tables, whereas the enthalpy for the state 4 must be calculated using vapor quality:

h_{3, v} = 2785 kJ/kg

h_{4, wet} = h_4,v x + (1 – x ) h_4,l  = 2576 . 0.694 + (1 – 0.694) . 174 = 1787 + 53.2 = 1840 kJ/kg

Then the work done by the steam, W_T, is

W_T = Δh = 945 kJ/kg

3)

Enthalpy for state 1 can be picked directly from steam tables:

h_{1, l} = 174 kJ/kg

State 2 is fixed by the pressure p₂ =  6.0 MPa and the fact that the specific entropy is constant for the isentropic compression (s₁ = s₂ = 0.592 kJ/kgK for 0.008 MPa). For this entropy s₂ = 0.592 kJ/kgK and p₂ =  6.0 MPa we find h_{2, subcooled} in steam tables for compressed water (using interpolation between two states).

h_{2, subcooled} = 179.7 kJ/kg

Then the work done by the pumps, W_P, is

W_P = Δh = 5.7 kJ/kg

4)

The enthalpy difference between (2 → 3), which corresponds to the net heat added in the steam generator, is simply:

Q_add = h_{3, v}  – h_{2, subcooled} = 2785 – 179.7 =  2605.3 kJ/kg

Note that there is no heat regeneration in this cycle. On the other hand, most of the heat added is for the enthalpy of vaporization (i.e., for the phase change).

5)

In this case, steam generators, steam turbine, condensers, and feedwater pumps constitute a heat engine that is subject to the efficiency limitations imposed by the second law of thermodynamics. In the ideal case (no friction, reversible processes, perfect design), this heat engine would have a Carnot efficiency of

η_Carnot = 1 – T_cold/T_hot = 1 – 315/549 = 42.6%

where the temperature of the hot reservoir is 275.6°C (548.7 K), the temperature of the cold reservoir is 41.5°C (314.7K).

The thermodynamic efficiency of this cycle can be calculated by the following formula:

thus
η_th = (945 – 5.7) / 2605.3 = 0.361 = 36.1%