Подскажите пожалуйста формулу, как найти КПД удара, зная массы тел?
Ученик
(131),
закрыт
9 лет назад
Трудное детство
Оракул
(70151)
9 лет назад
КПД=(Е1-Е2)/Е1=1-Е2/Е1, где Е1 и Е2 суммарные кинетические энергии системы (молоток+наковальня) до и после удара. пусть начальная скорость молотка v1, а наковальни v2, конечная скорость молотка u1, а наковальни u2. решая совместно уравнения закона сохранения импульса и закона сохранения энергии находим u1=((m1-m2)v1+2m2v2)/(m2+m1), u2=((m2-m1)+2m1v1)/(m2+m1). учитывая что v2=0, получаем u1=-v1(m2-m1)/(m2+m1), u2=2m1v1/(m2+m1). тогда E2/E1=((m2-m1)^2+4m1^2)/m1(m2+m1)^2=0,17. и КПД=1-0,17=0,83.

Пример решения задачи по определению коэффициента полезного действия (КПД) при соударении свободных твердых тел.
Задача
Молот весом G1 = 40 кН падает на наковальню с высоты h = 2 м. Вес наковальни вместе с куском металла, подвергающимся ковке, равен G2 = 360 кН.
Рассматривая удар молота о наковальню как удар свободных тел, найти коэффициент полезного действия молота.
Другие примеры решений >
Помощь с решением задач >
Решение
Коэффициент полезного действия равен отношению полезной работы к работе, затрачиваемой на приведение механизма в движение.
В данном случае полезной является работа, израсходованная на деформацию металла. Эта работа равна потере кинетической энергии тел при ударе T0−T.
Работа, затрачиваемая на подъем молота, равна увеличению его потенциальной энергии G1h. При падении молота его потенциальная энергия переходит в кинетическую.
Таким образом, затрачиваемая работа равна кинетической энергии тел до удара T0.
Коэффициент полезного действия молота:
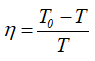
или
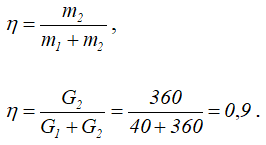
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
-
Кпд удара
Физический
удар
– совокупность явлений, возникающих при
столкновении твердых тел в условиях
изменения их скоростей от начальных до
конечных за малый промежуток времени,
исчисляемый тысячными (или менее) долями
секунды. В процессе деформации тел при
ударе развиваются ударные силы. Импульсы
этих сил за время удара во много раз
больше импульсов всех внешних сил,
приложенных к системе соударяющихся
тел. Поэтому в процессе удара влиянием
внешних сил можно пренебречь и
считать, что система соударяющихся тел
является замкнутой, а ударные силы
-внутренними. В такой системе обязательно
выполняется закон сохранения количества
движения.
Процесс
физического удара двух твердых тел
разделяется на две фазы. В течение первой
– нагрузочной
– происходит монотонное нарастание
ударных сил, так как кинетическая энергия
преобразуется в энергию упругого
деформирования сталкивающихся тел в
месте их контакта. После максимального
сближения, соответствующего максимуму
ударной силы, начинается вторая фаза
процесса –разгрузочная
– с монотонным спадом ударных сил вплоть
до прекращения контакта тел. Размеры и
форма тел восстанавливаются. За счет
возврата упругой энергии происходит
восстановление уровня кинетической
энергии, полное в идеальной и ограниченное
в реальной системе.
Математические
соотношения, базирующиеся на представлениях
о физическом ударе, достаточно просты.
Так, для центрального удара двух свободных
масс m
и М
с
нормальными скоростями v0
и vM
в начале соударения, скоростью vc
в конце первой фазы, когда обе массы
двигаются как единая система, vk
и vMk
в конце второй фазы условие неизменности
количества движения запишем в виде
m
v0
+ М
vM
= (m
+ М)
vc
= mvK
+ МvMk
. (1.1)
При идеально
упругом ударе (без учета каких-либо
потерь), когда нагрузочный и разгрузочный
импульсы равны, дополнительным уравнением
для определения скоростей является
условие сохранения величины кинетической
энергии:
![]() . (1.2)
. (1.2)
Указанные
соотношения раскрывают только скоростное
состояние соударяющихся тел и ничего
не говорят о силах (функция Р
(t)
остается неизвестной), деформациях, или
волнах напряжений, порождаемых этими
силами и приводящих к колебательным
процессам.
Динамика системы
из двух сталкивающихся масс молота в
условиях так называемого «жесткого»
удара лишь с определенной степенью
приближения может быть охарактеризована
скоростными соотношениями (1.1). В
нормальных условиях эксплуатации
между сталкивающимися массами
закладывается металл и развивающиеся
ударные силы вызывают в нем пластическое
течение. Происходит рабочий ход с
заданным технологическим нагружением.
Это уже не соударение твердых упругих
тел, а упругопластический удар со своими
закономерностями. Тем не менее можно
считать, что система по-прежнему замкнута,
так как усилие, действующее на металл,
уравновешено реакцией связи основания
(шабота), встречных подвижных частей
или рамы. Следовательно, можно считать,
что количество движения осталось без
изменения, произошло только его
перераспределение между столкнувшимися
массами. Однако в итоге удара общий
уровень кинетической энергии в
системе уменьшается вследствие
необратимых потерь, обусловленных
пластической деформацией (не учитывая
рассеяния энергии на колебания и т.
п.). Необратимость потерь сразу же
устраняет возможность однозначного
определения конечных скоростей, так
как исчезло дополнительное условие
(1.2). Поэтому для реального удара вводят
эмпирический коэффициент восстановления
(отскока), устанавливающий соотношение
между проекциями скоростей на линию
центров до и после удара:
![]() (1.3)
(1.3)
При пользовании
формулой (1.3) необходимо помнить о системе
отсчета и полярности скоростей.
Для
идеально упругого удара разгрузочный
импульс равен нагрузочному и k0
= 1.
Для
шаботного молота начальная скорость
шабота vM
= 0, поскольку последний опирается на
подшаботную прокладку, фундамент и
грунт. Подшаботная прокладка, обладая
определенной жесткостью, вызывает
отпор, однако опыт показывает, что
влияние отпорного импульса невелико,
поэтому при анализе энергетики им можно
пренебречь и считать шабот свободным.
Тогда получаем систему уравнений:
m
v0
= (m
+ М)
vc
= mvk
+ МvMk
. (1.4)
k0
v0
= vMk
– vk
,
на основании
которой определяем конечные скорости:
 (1.5)
(1.5)
Поскольку
кинетическая энергия к началу удара
![]() (1.6)
(1.6)
а после его окончания
![]() (1.7)
(1.7)
устанавливаем
работу пластической деформации
![]() (1.8)
(1.8)
Следовательно,
энергетический к. п. д. удара, т. е.
отношение полезно используемой энергии
к ее начальной величине,
![]() (1.9)
(1.9)
г де
де![]() — коэффициент масс.
— коэффициент масс.
Зависимость
коэффициента kM
от соотношения масс М
и
m
имеет резко затухающий до нуля характер
при М/m
< 10 (рис. 1.5). Такова же и зависимость у
= f(М/m)
при k0
= const. Поэтому более чем десяти-пятнадцатикратное
превышение массы шабота над массой
падающих частей не дает экономически
целесообразного выигрыша в расходе
энергии.
Рис. 1.5. Зависимость КПД удара от
соотношения масс
Потенциал
упругой энергии в молоте зависит от
того, как происходит перераспределение
кинетической энергии при ударе. При
большом поглощении энергии на упругое
деформирование интенсивнее происходит
и разгрузка, следовательно, сильнее
восстанавливается вновь уровень
кинетической энергии и больше коэффициент
восстановления. Непосредственное
влияние на этот процесс оказывает
соотношение между упругими и пластическими
свойствами системы. Например, если бы
обрабатываемый металл обладал идеальной
пластичностью, а элементы конструкции
молота были абсолютно твердыми, то
разгрузочный импульс отсутствовал и
вторая фаза удара характеризовалась
бы условием k0
= 0. В действительности k0
> 0 и тем больше, чем выше усилие
деформации, необходимое для осуществления
технологического нагружения. В интервале
температур ковки-штамповки для схем
деформации с невысокой резкостью
напряженного состояния (операции ковки,
заготовительные переходы объемной
штамповки) k0
= 0,15… 0,40, тогда как при доштамповке в
окончательном ручье молотового штампа
k0
= 0,50….0,65, а при очень жестких ударах
штампа по штампу увеличивается до k0
= 0,75….0,80.
Для бесшаботных
молотов удар является столкновением
двух свободных масс и поэтому
![]() (1.10)
(1.10)
где
 (1.11)
(1.11)
Соседние файлы в папке Молоты
- #
- #
- #
- #
- #
Технологии машиностроения
УДК 621.735.004:621.974.001
ВАРИАНТ ВЫЧИСЛЕНИЯ КПД УДАРА ПРИ ДЕФОРМИРОВАНИИ МЕТАЛЛА И.А. Чечета, В.В. Долгополова, А.Е. Чечета
Изложен порядок вычисления КПД удара при высокоскоростной штамповке сплошного металла и сыпучего материала в виде измельченной металлической стружки Ключевые слова: штамповка, удар, КПД
1. Исходные предпосылки. В заготовительном производстве перечнем оборудования ударного действия охвачены высокоскоростные молоты (ВСМ), машины импульсного брикетирования (МИБ) металлической стружки и другие копры и испытательные стенды, располагающие диапазоном скорости удара 10 -^50 м/с [1]. Отличительной особенностью такого технологического оборудования является формирование энергии удара за счёт работы расширения накапливаемого в приводе газа высокого давления. В общем случае накапливаемым газом может быть сжатый азот или газообразные продукты преобразований вводимого энергоносителя, например, в результате сгорания стехиометрической смеси пропана с баллонным кислородом или воздухом. Известно, что моли газов, составляющих горючую газовую смесь, занимают равные объёмы при равных давлениях и температуре, а объём газа обратно пропорционален давлению, Это даёт возможность устанавливать требуемое количество заряда топливной смеси по показаниям манометров, располагаемых на магистралях подачи топливных компонент.
Отечественные ВСМ и МИБ, ориентированные на применение именно этой горючей газовой смеси, показали приемлемую для практики работоспособность. Поэтому исследование эффективности удара, характерного для машин упомянутого назначения, продолжает оставаться актуальным.
Известно [2], что скорость силового воздействия является наиболее существенным фактором, предопределяющим поведение материалов при ударе. При этом замечено [3], что сопротивление скоростному удару резко перераспределяет положение металлов в ряду,
Чечета Иван Алексеевич – ВГТУ, д-р техн. наук, профессор, тел. (473) 222-53-85
Долгополова Валерия Валерьевна – ВГТУ, инженер, тел. (473) 220-92-68
Чечета Антон Евгеньевич – ВГУ, инженер, тел. (473) 272-26-77
который они образуют по результатам обычных (статических) испытаний на прочность.
В число основных показателей эффективности высокоскоростного оборудования входит коэффициент полезного действия (КПД) п удара.
1.1. Общее понятие о КПД удара. Обычно количественную величину КПД п удара оценивают отношением энергии Ед, по назначению затрачиваемой на пластическое деформирование, к исходному запасу эффективной энергии Ео до удара:
П = Ед / Е0. (1)
При этом имеют в виду, что баланс расходования энергии Ео представляется в виде:
Ео = Ед + Еу + Еп , (2)
где Еу – энергия на упругое деформирование, сопровождающее удар; это деформирование по эксплуатационным соображениям, касающихся работоспособности энергетически активных масс ВСМ, полностью отнесено к элементам, передающим силу Р удара, а после удара за счёт этой доли энергии возникает подскок бойка – верхней энергетически активной массы (эффект частичного восстановления кинетической энергии, затрачиваемой на удар);
Еп – доля теряемой энергии (диссипация энергии). Эта доля в рассматриваемых условиях достаточно мала и отдельно в расчётах не учитывалась.
В результате баланс расходования энергии принят в виде:
Ео = Ед + Еу. (3)
Тогда уравнение для вычисления КПД удара получает вид:
П=(Ео-Еу)/Ео=1-(Еу /Ео). (4)
Так как Ео = 0,5Муо2, а Еу = 0,5Муп2, и приведенная массаМ = т1 т2/(т1+ т2), то уравнение (4) преобразуется к виду:
П=1- Уп2/Уо2 , (5)
где уо, уп – начальная скорость удара и скорость подскока после соударения.
Поскольку объектом пластического деформирования может быть и сплошной материал (при объёмной штамповке на ВСМ), и сыпучее тело в виде дроблённой металлической стружки (при брикетировании на МИБ), то представляется необходимым конкретно проанализировать КПД удара для каждого из этих случаев.
1.1.1.КПД удара при скоростной штамповке сплошного материала. Числовое соотношение между скоростями уо и п являющимися основными показателями уравнения (5), представляется возможным установить экспериментально. Для такого эксперимента надо:
– вдоль рабочего хода бойка установить линейку с метрической шкалой;
– назначить базовое расстояние S, на котором скорость уо можно считать постоянной, например, 5 мм между нижним торцем подлетающего бойка, наносящего удар, и верхним торцем образца, подлежащего пластическому деформированию;
– одновременно включить рабочий ход бойка и высокоскоростную кинокамеру;
– зафиксировать число фотокадров, отражающих прохождение бойком базового расстояния S, а также – высоты подскока бойка относительно метрической шкалы установленной линейки;
– зная частоту и количество кадров, величину базового пути S, вычислить скорость уо, а скорость уп – по частоте и количестве кадров, на которых зафиксирован путь подскока бойка относительно метрической шкалы установленной линейки;
– найденные величины скоростей использовать для вычисления КПД удара по уравнению (5).
Экспериментальные исследования, выполненные в ЭНИКМАШе по изложенной методике [4], показали, что КПД удара имевшихся ВСМ при холодной динамической осадке стальных и алюминиевых образцов находится в диапазоне 0,91^0,98. При этом отмечено, что более высокое значение КПД характерно для высокоскоростной штамповки алюминиевых образцов.
Основные недостатки экспериментальной проверки КПД удара по изложенной методике:
– неприемлемость реализации экспериментального способа в производственных условиях;
– исключена возможность предварительной оценки КПД на этапе проектирования как ВСМ, так и технологического процесса высокоскоростной штамповки.
1.1.2. Теоретический анализ КПД удара.
Для выполнения теоретического анализа КПД удара приняты следующие основные предпосылки и условия.
а) Силовая система молота имеет замкнутую схему, при которой пластически деформируемый объект (образец) одновременно подвергается удару сверху и снизу энергетически активными массами (т1 и т2).
б) Масса пластически деформируемого образца очень мала (<<3% по сравнению с энергетически активными массами) и в расчётах не принята во внимание.
в) Упругие деформации отнесены к энергетически активным массам, передающим деформирующую силу, а весь объём пластической деформации сосредоточен в образце, материал которого ведёт себя как идеальное жестко пластичное тело [5].
Для замкнутой силовой системы рассматриваемых ВСМ уравнения движения энергетически активных масс имеют вид:
т1^1М^=-Р; (6)
т2(ёу2/&) =-Р. (7)
С учётом одновременного соударения энергетически активных масс мгновенная скорость V удара является суммой у=у1+у2, а в каждый момент деформирования
v=dh/dt, (8)
где h текущая высота образца за единицу времени t.
Тогда математическими преобразованиями уравнений (6), (7), (8) уравнение деформирования приводится к виду:
vdv=-(P/M)dh. (9)
Сила, предопределяющая упругую деформацию сжатия:
р=°£ , (10)
где &(=£вЕ – напряжение, предопределяемое текущей степенью £в деформации восстановления и модулем упругости Е;
^=У/Ь – площадь поперечного сечения;
V, Ь – объём и текущая высота деформируемого образца, соответственно.
Предельное значение истинной относительной деформации 8$ на этапе упругого восстановления высоты образца h0ст, соответствующего моменту прекращения контакта между бойком и пластически деформируемым образцом:
8$ ln(hост/hmin), (11)
где hmin – высота образца в момент, когда величина внешней деформирующей силы имела своё максимальное значение при скорости удара v=0, то есть в конце удара.
Соответственно,
Кст^е^^Ло)^^. (12)
Текущее значение истинной относительной деформации на этапе восстановления кинетической энергии;
8в=1п(Ьост/Ь), (13)
а с учётом уравнения (12) –
8iв 8 (8т-8$). (14)
В результате текущее значение силы подскока на рассматриваемом участке деформирования:
Р = УЕ[8-(8т- 8)]/К (15)
С учётом уравнения (15) уравнение (9) приводится к виду:
vdv=-(VE/M)[8i-(8m- 8s)]d8l.. (16)
Решение уравнения (16) с условием, что 81=8т при ^0, представляет собой закон изменения скорости на этапе восстановления кинетической энергии:
V = {(VE/M)[(8m2- 82) -(8т- 8^- 8г)]}°5 . (17)
В момент времени, когда 81=8п-8$, скорость достигает своего предельного значения v=vп (скорость подскока бойка после соударения с пластически деформируемым образцом) и уравнение (17) преобразуется к виду:
Vп= Vо(8s/28m)a5, или vП2 Ыо =8$./28ш (18)
С учётом найденного соотношения квадратов скоростей уравнение (5) получает вид: П=1-8Д8т (19)
Поскольку 8$=о/Е, уравнение (19) преобразуется к виду:
П=1- о/28„Е. (20)
Пользуясь уравнением (20), не следует забывать, что величина не является пределом текучести (или близкими к нему пределами упругости и пропорциональности). Все эти пределы условны и характерны только для статических испытаний материалов на прочность. Статические испытания, во избежание появления инерционных сил, реализуют при очень медленном росте прикладываемой деформирующей силы. Попутно в процессе испытаний постоянно автоматически взвешивают прикладываемую силу и измеряют удлинение образца. Результатом статических испытаний является создаваемая кривая упрочнения в координатах «о-8», где 8=!п^(уЪ). Здесь hо и h
– начальный и текущий размеры длины испытываемого образца.
Статические испытания, как правило, ведут при растяжении образца.
Динамические испытания материалов на прочность ориентированы только на сжатие образца. Деформирующую силу прикладывают с большой скоростью, которую измеряют на базовом участке S и, отсчитав время прохождения бойком этого базового участка, вычисляют начальную скорость vо удара. Зная массу
m1 бойка, вычисляют энергию удара
Ео=0,5m1vо2, считая, что M~m1 (из-за малости массы m1 по сравнению с массой т2). Применительно к объёму V испытываемого образца вычисляют величину приходящейся на него удельной энергии еуд=Е/V, а измерениями испытанного образца определяют 8т=1п(Ъ^т1п) Выполнив серию ударов с очередными значениями vо, вычерчивают график в координатах
«еуд 8т».
Так как еуд=а$8т, то на основании полученного графика для каждого значения скорости vо вычисляют величину динамического напряжение а6.. В свою очередь, следует принимать во внимание, что модуль упругости Е в динамических условиях деформирования не изменяется, а сам пластически деформируемый материал ведёт себя как идеальное жёстко пластичное тело, но есть возможность вычислять величину 8х=ах/Е.
В качестве примера в таблице представлены результаты вычисления КПД п удара для алюминиевого сплава Д16Т и меди М3.
Алюминиевый сплав Д16′
Ув, м/с eуд, МПа 8т п
13,33 0,502 0,12 0,975
15,68 0,687 0,14 0,975
18,18 0,920 0,19 0,981
20,00 1,113 0,25 0,987
21,74 1,329 0,28 0,986
23,22 1,505 0,32 0,989
25,10 1,760 0,37 0,991
Медь МЗ
14,20 0,470 0,13 0,988
14,28 0,475 0,14 0,989
19,43 0,880 0,27 0,995
22,22 1,150 0,35 0,996
22,50 1,180 0,36 0,996
24,28 1,362 0,43 0,996
26,23 1,603 0,49 0,997
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Вывод. Основным достоинством выполненного математического анализа КПД удара является то, что, зная величину упругой предельной деформации 8$ обрабатываемого материала и требуемое значение максимальной истинной относительной деформации 8п1 проектируемого технологического процесса высокоскоростной штамповки, есть возможность предварительно получать представление о степени полноты использования вводимой энергии в технологическую систему.
1.1.3. КПД удара при брикетировании стружки. Для анализа процесса брикетирования приняты условия, достаточные для приемлемого выбора начальной высоты hо брикета, начальной скорости vо удара и степени а пористости получаемого брикета.
Необходимость выбора начальных величин hо и vо обусловлена тем обстоятельством, что брикетирующий пуансон (масса т1 машины МИБ), соприкоснувшийся с поверхностью стружки, свободно засыпанной в матрицу, на некотором дальнейшем отрезке своего пути имеет практически незаметное сопротивление со стороны стружки. Поэтому для составления методики к вычислению КПД брикетирующего удара принята экспериментально обоснованная рекомендация [6], состоящая в том, что для брикетирования, например, алюминиевой стружки начальную высоту hо приемлемо отсчитывать с момента, когда пуансон проходит 40% своего пути, начиная от первичного контакта между пуансоном и свободно лежащей в матрице стружкой. Это даёт основание считать, что найденному таким образом значению hо соответствует начальная скорость vо перемещающегося пуансона.
Понятием о степени а пористости оценивается возможность брикета не разрушаться в процессе транспортировки и не сгорать, а плавиться при загрузке в плавильную высокотемпературную ёмкость. Исходя из таких соображений, степень а пористости брикета в среднем должна составлять а=0,5^0,7 по сравнению со сплошным материалом, для которого считают а=1.
Одним из вариантов получения брикетов с достаточной для практики степенью а пористости является брикетирование стружки в матрице с цилиндрической рабочей поверхностью. В этом случае ликвидация пористости в изготовляемом брикете идёт исключительно за счёт осадки стружки в осевом направлении. То есть, величина истинной относительной деформации 8 всегда остаётся численно равной степени а пористости брикета.
Сила Р, затрачиваемая на осадку стружки, в определённой мере расходуется на упругое деформирование силопередающих элементов (стяжных шпилек МИБ). Энергия, расходуемая на это деформирование, впоследствии предопределяет некоторое восстановление кинетической энергии соударяющихся масс (подскок). Если абсолютное изменение линейного Ahу размера силопередающих элементов выражено в долях высоты осаживаемого брикета, то соотношение работы, выполняемой силой Р, и энергии Еу имеет вид:
РАЬу =0, 5Му2 . (21)
Так как упругая относительная деформация составляет определённую долю £ от деформации 8т =1п(Ъ^т1п), то д=А^ /Ъо= &т. Следовательно,
Аhу = &тК. (22)
Тогда уравнение (21) принимает вид:
Р =0,5 Шп2/&„}10. (23)
Для сплошного материала напряжение на участке упругого деформирования составляет а=&тЕ, где Е – модуль упругости материала силопередающих элементов МИБ. Следовательно, при брикетировании для оценки величины деформирующей силы Р необходимая корректировка обеспечивается введением степени а пористости брикета:
Р=&тЕа^К, (24)
где V – объём брикета.
(Здесь и далее по тексту все геометрические размеры, касающиеся деформирования, отнесены к геометрическим размерам получаемого брикета). В свою очередь, степенью а пористости скорректирована и величина удельной энергии еудбр брикетирования:
еуд.бр. Ео!аУ. (25)
Поскольку для сплошного материала еуд=Е/V, то для пористого еудбр=еуд/а=о!18т/а, а так как 8т=а, удельная энергия брикетирования, равная динамическому напряжению возни-
кающему в сплошном материале при ударе.
Сила удара для получения брикета составляет:
Р=а^/^. (26)
Тогда сопоставление энергии, вычисляемых по уравнениям (23) и (26) даёт результат;
/ v02=Gs/Е. (27)
В итоге с учётом уравнения (5) КПД удара при брикетировании стружки составляет: ц=1-о/Е (28)
Реализуемые в современном производстве технологии брикетирования стружки содержат в себе исходные условия, пригодные для конкретизации требований к выбору величины динамического напряжения сплошного материала, из которого получена стружка. Так, в процессе подготовки стружки к брикетированию стружку дробят, очищают с промывкой, сушат, термически обрабатывают для снятия наклёпа, появившегося в процессе стружкооб-разования. Дополнительной операцией в подготовке стружки должна быть выборочная проверка на твёрдость элементов стружки. Такая проверка необходима для того, чтобы формировать представление о средней твёрдости стружечного материала. С учётом этого из сплошного металла, такого же, как металл стружки, при такой же его твёрдости следует изготовлять стандартизованные образцы для испытаний на динамическое сжатие (осадку).
Методика таких испытаний известна [7,
8]. Последовательно наносят на каждый образец по удару в диапазоне скорости намечаемого брикетирования.
По результатам испытаний составляют график в координатах «еуд-8», а по соотношению еуд=о!!8т вычисляют величину возникающего динамического напряжения а6..
Вывод. Для вычисления КПД удара при брикетировании используется степень деформации 8т изготавливаемого брикета и динамическое напряжение сплошного металла, из которого получена брикетируемая стружка, а также имеющийся в справочниках модуль упругости Е материала, из которого изготовлены конструктивные элементы МИБ, передающие силу удара.
Литература
1. Кононенко В.Г. Высокоскоростное формоизменение и разрушение металлов. – Харьков: Изд. «Вища школа». 1980. – 232 с.
2. Давиденков Н.Н. Динамические испытания матал-лов. – М.: ОНТИ, 1936.
3. Высокоскоростное деформирование металлов /Под редакцией А.М. Шахназарова. – М.: Машиностроение. -1966. – 175 с.
4. Согришин Ю.П., Гришин Л.Г., Воробьёв В.М. Штамповка на высокоскоростных молотах. – М.: Машиностроение, 1978, 167 с.
5. Орленко Л.П. Поведение материалов при интенсивных динамических нагрузках.- М.: Машиностроение, 1964, 242 с.
6. Букин Ю.М,,Шалбоян А., Филянов А.,Райзман Д.А Определение энергетических параметров импульсной брикетировочной машины типа МИБ-165Т. /Обработка металлов давлением в машиностроении, вып.9. – Харьков: Изд. ХГУ. 1973, с.100-103.
7. Чечета И.А. Способ динамической тарировки датчиков усилия / А.с. СССР № 828014, 1981. Бюл. № 17.
8. Чечета И.А. , Бородкин В.В. Определение технологических возможностей высокоскоростных молотов /Пластическое формообразование деталей авиационной техники. Межвуз. сб. – Казань: КАИ. 1983. Стр. 110-115.
Воронежский государственный технический университет Воронежский государственный университет
THE VERSION OF CALCULATION THE EFFICITNCY AT HIGT SPEED METALS
DEFORMATION ГА. Checheta, V.V. Dolgopolova, A^. Checheta
The versions of calculation the laboratory devices of efficiency at high speed metals deformation are discussed end
calculated
Key words: deformation, impact, efficiency
Решение.
Кинетическая энергия бойка перейдет в кинетическую энергию совместного движения бойка и сваи. В результате неупругого взаимодействия бойка и сваи часть энергии пойдет на нагревание тел. Запишем формулу для определения КПД неупругого удара.
[ eta =frac{{{W}_{KBC}}}{{{W}_{KB}}} (1). ]
WКВ – кинетическая энергия бойка, WКВС – кинетическая энергия бойка и сваи.
Для определения скорости совместного движения бойка и сваи используем закон сохранения импульса для неупругого взаимодействия. Покажем рисунок.
[ {{m}_{1}}cdot {{vec{upsilon }}_{1}}=({{m}_{1}}+{{m}_{2}})cdot vec{upsilon }. ]
Находим проекции на ось Ох:
[ {{m}_{1}}cdot {{upsilon }_{1}}=({{m}_{1}}+{{m}_{2}})cdot upsilon , upsilon =frac{{{m}_{1}}cdot {{upsilon }_{1}}}{{{m}_{1}}+{{m}_{2}}} (2). ]
Запишем формулы для определения кинетической энергии бойка и сваи.
[ {{W}_{KB}}=frac{{{m}_{1}}cdot upsilon _{1}^{2}}{2} (3), {{W}_{KBC}}=frac{({{m}_{1}}+{{m}_{2}})cdot {{upsilon }^{2}}}{2} (4). ]
(2) подставим в (4) (3) и (4) подставим в (1) определим КПД.
[ begin{align}
& {{W}_{KBC}}=frac{({{m}_{1}}+{{m}_{2}})cdot m_{1}^{2}cdot upsilon _{1}^{2}}{2cdot {{({{m}_{1}}+{{m}_{2}})}^{2}}}=frac{m_{1}^{2}cdot upsilon _{1}^{2}}{2cdot ({{m}_{1}}+{{m}_{2}})} (5). \
& eta =frac{frac{m_{1}^{2}cdot upsilon _{1}^{2}}{2cdot ({{m}_{1}}+{{m}_{2}})}}{frac{{{m}_{1}}cdot upsilon _{1}^{2}}{2}}=frac{{{m}_{1}}}{({{m}_{1}}+{{m}_{2}})} (6). \
end{align} ]
η = 80 %.
« Последнее редактирование: 06 Апреля 2015, 06:34 от alsak »

Записан
