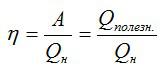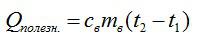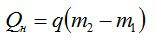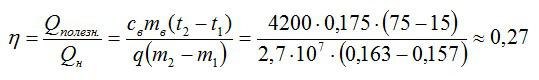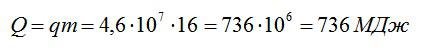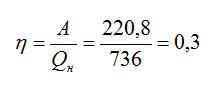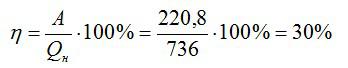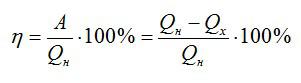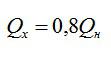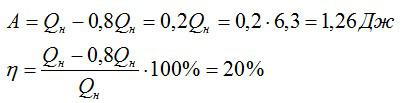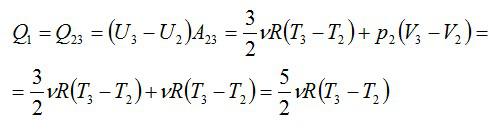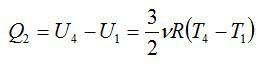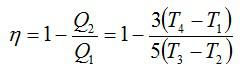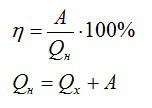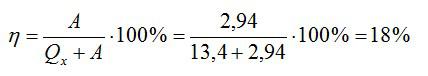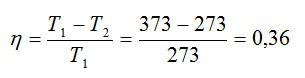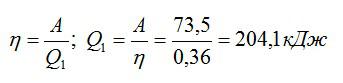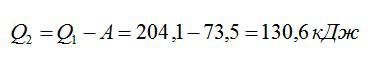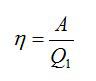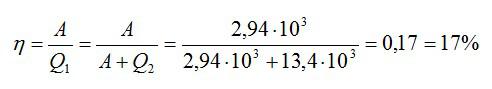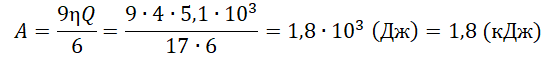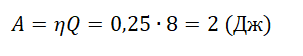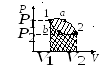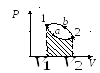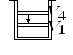Как найти кпд за цикл работы получает

На этой странице вы узнаете

• В чем прелесть фазовых переходов?
• Что лучше выбрать: Mercedes или BMW?

Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов,а именно получать тепловую энергию различными доступными способами. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне. 

Тепловые машины и их КПД

Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.

Мы не почувствуем, как испарится капелька у нас на руке, потому что это не требует много тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. А зачем мы вообще рассматриваем эти фазовые переходы? Все дело в том, что именно фазовые переходы являются ключевым звеном во всех процессах, где нас просят посчитать КПД, от них нашему рабочему телу и подводится теплота нагревателя.

Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.

Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую. 

Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в автомобилях часть энергии от сгоревшего бензина идет на движение. Схематично можно изобразить так:

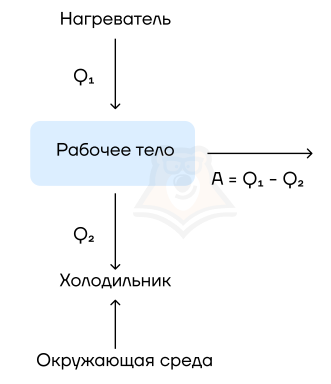
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q₁, из которой A уходит на работу механизма. Остаток теплоты Q₂ рабочее тело отдает холодильнику, по сути — это потеря энергии.

Физика не была бы такой загадочной, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:

Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.

Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери. 

Полезную работу можно расписать как Q₁ — Q₂ (по закону сохранения энергии). Тогда формула примет вид:

(eta = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})

Цикл Карно

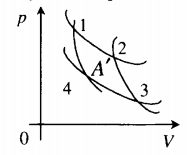
Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже все сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат. Рассмотрим, как этот цикл выглядит в координатах p(V).

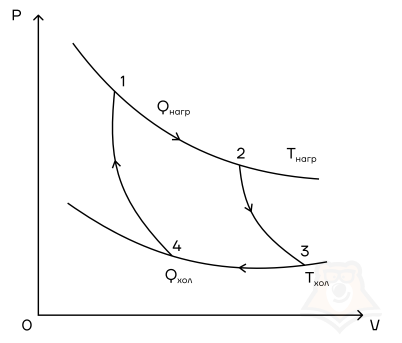
• Температура верхней изотермы 1-2 — температура нагревателя (так как теплота в данном процессе подводится).
• Температура нижней изотермы 3-4 — температура холодильника (так как теплота в данном процессе отводится).
• 2-3 и 4-1 — это адиабатические расширение и сжатие соответственно, в них газ не обменивается теплом с окружающей средой.

Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД. 

Формула, по которой можно рассчитать ее КПД выражается через температуры:

Приступим к задачам

Задачи на данную тему достаточно часто встречаются в задании 27 из КИМа ЕГЭ. Давайте разберем некоторые примеры.

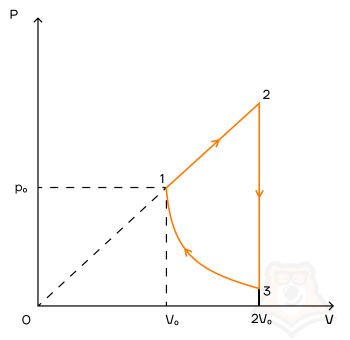
Задание 1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A₁₂ = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Q_хол| = 4780 Дж. Найдите работу газа |A₁₃| на адиабате, если количество вещества постоянно.

Решение:

Шаг 1. Первое, с чего лучше начинать задачи по термодинамике — исследование процессов. 

Посмотрим на участок 1-2 графика: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: (frac{pV}{T} = const). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем.  Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.

Участок 2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: (frac{p}{T} = const). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.

Участок 3-1: адиабата по условию, то есть количество теплоты в этом переходе равна нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем. 

Оформим все данные в таблицу. 

Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.

Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.

Шаг 2. Первый закон термодинамики для процесса 1-2 запишется в виде: 

Q₁₂ = ΔU₁₂ + A₁₂. 

Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции: 

(A_{12} = frac{p_0 + 2p_0}{2} * V0 =frac{3p_0V_0}{2}). 

Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:

(Delta U_{12} = frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = frac{9p_0V_0}{2}). 

Заметим, что это в 3 раза больше работы газа на этом участке: 

(Delta U_{12} = 3A_{12} rightarrow Q_{12} = 4A_{12}).

Шаг 3. Работа цикла — площадь фигуры, которую замыкает график, тогда . A = A₁₂ — |A₃₁|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q₁₂ — |Q₃₁|.

 Сравним эти формулы:

Q₁₂ -|Q₃₁| = A₁₂ — |A₃₁|,

подставим выражения из предыдущего пункта:

4A₁₂ — |Q₃₁| = A₁₂ — |A₃₁| (rightarrow) |A₃₁| = -3A₁₂ + |Q₃₁| = -31520 + 4780 = 220 Дж.

Ответ: 220 Дж

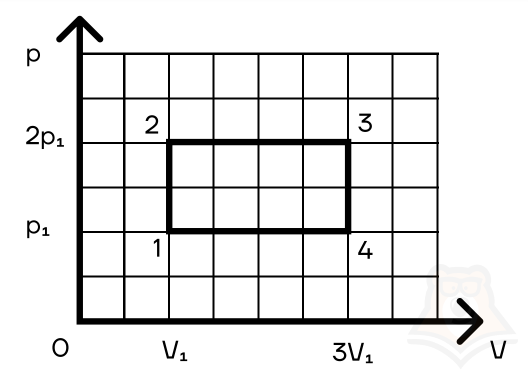
Задание 2. Найти КПД цикла для идеального одноатомного газа.

Решение:

Шаг 1. КПД цикла определим по формуле: (eta = frac{A}{Q}), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p₁ — p₁)(3V₁ — V₁) = 2p₁V₁.

Шаг 2. Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:

Посмотрим на участок 1-2 графика: давление растет, объем не меняется. По закону Шарля (frac{p}{T} = const) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.

2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака (frac{V}{T} = const) температура тоже растет, растет и внутренняя энергия.

3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.

4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.

Оформим данные в таблицу: 

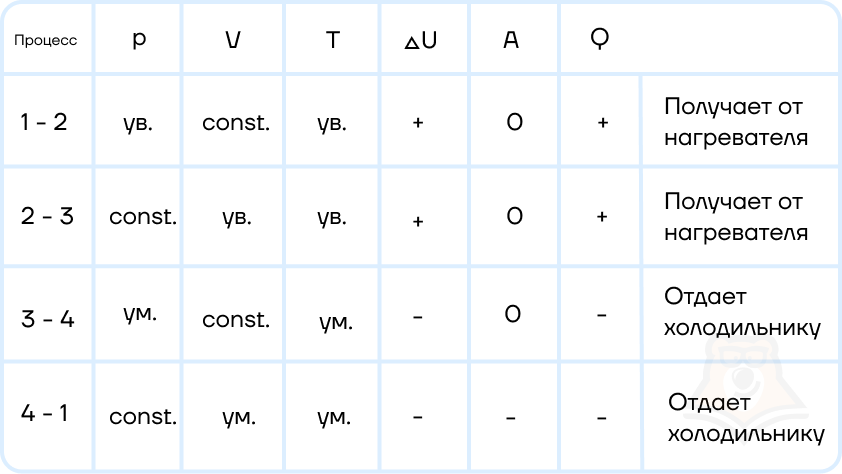
Отметим, что  необходимое Q = Q₁₂ + Q₂₃.

Шаг 3. Запишем первый закон термодинамики для процессов 1-2 и 2-3:

(Q_{12} = U_{12} + A_{12} = Delta U_{12} = frac{3}{2}(2p_1V_1 -p_1V_1) = frac{3}{2}p_1V_1).
(Q_{23} = Delta U_{23} + A_{23}), работу газа найдем как площадь под графиком: A₂₃ = 2p₁(3V₁ — V₁) = 4p₁V₁.
(Delta U_{12} = frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1).
(Q_{23} = Delta U_{23} + A_{23} = 10p_1V_1).

Шаг 4. Мы готовы считать КПД: (eta = frac{A}{Q} = frac{A}{Q_{12} + Q_{23}} = frac{2p_1V_1}{frac{3}{2}p_1V_1 + 10p_1V_1} = frac{4}{23} approx 0,17).

Ответ: 17%

Теперь вас не должно настораживать наличие графиков в условиях задач на расчет КПД тепловых машин. Продолжить обучение решению задач экзамена вы можете в статьях «Применение законов Ньютона» и «Движение точки по окружности».

Фактчек

• Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую. 
• Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
• Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
  (eta = frac{A}{Q_1} = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})  
• Цикл Карно — цикл с максимально возможным КПД: (eta = frac{T_1 — T_2}{T_1} = 1 — frac{T_2}{T_1})
• Не забываем, что работа считается, как площадь фигуры под графиком.

Проверь себя

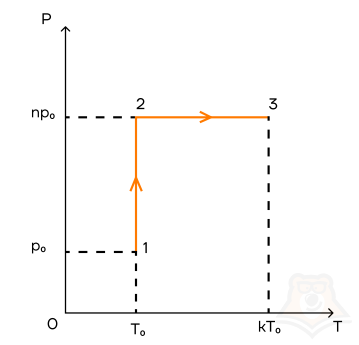
Задание 1. 
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T₀ = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.

1. 5672 Дж
2. 4731 Дж
3. 5817 Дж
4. 6393 Дж

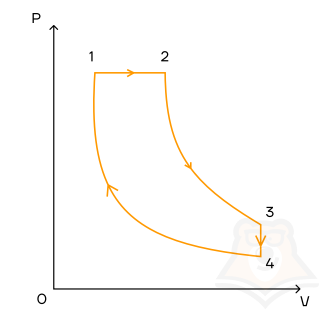
Задание 2. 
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT₁₂ к изменению его температуры ΔT₃₄ при изохорном процессе равен 1,5. Определите КПД цикла.

1. 0,6
2. 0,5
3. 0,8
4. 1

Задание 3.
В топке паровой машины сгорело 50 кг каменного угля, удельная теплота сгорания которого равна 30 МДж/кг. При этом машиной была совершена полезная механическая работа 135 МДж. Чему равен КПД этой тепловой машины? Ответ дайте в процентах.

1. 6%
2. 100%
3. 22%
4. 9%

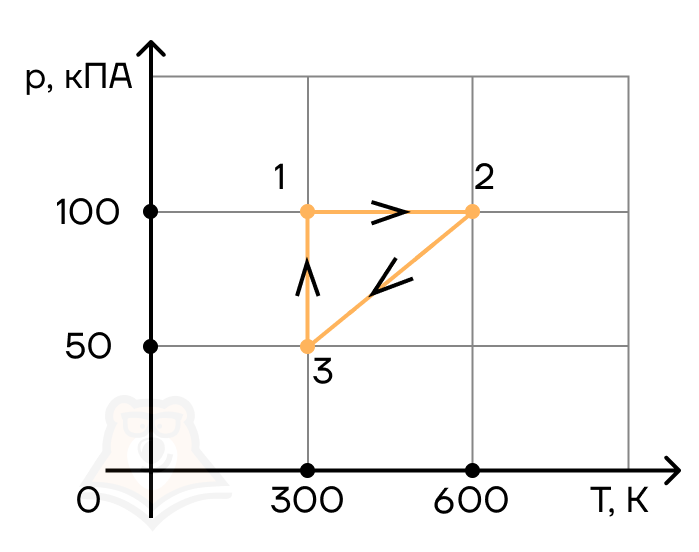
Задание 4.
С двумя молями одноатомного идеального газа совершают циклический процесс 1–2–3–1 (см. рис.). Чему равна работа, совершаемая газом на участке 1–2 в этом циклическом процессе?

1. 4444 Дж
2. 2891 Дж
3. 4986 Дж
4. 9355 Дж

Ответы:1 — 3; 2 — 1; 3 — 4; 4 — 3.

У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.

Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.

Задачи по физике на КПД теплового двигателя

Задача на вычисление КПД теплового двигателя №1

Условие 

Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.

Решение

Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:

Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:

Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.

Подставляем значения и вычисляем:

Ответ: 27%

Задача на вычисление КПД теплового двигателя №2

Условие

Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.

Решение

Найдем общее количество теплоты, которое произвел двигатель:

Теперь можно рассчитать КПД:

Или, умножая на 100, получаем значение КПД в процентах:

Ответ: 30%.

Задача на вычисление КПД теплового двигателя №3

Условие

Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.

Решение

КПД идеальной тепловой машины:

По условию:

Вычислим сначала работу, а затем КПД:

Ответ: 20%; 1,26 Дж.

Задача на вычисление КПД теплового двигателя №4

Условие

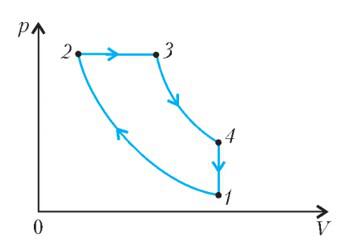
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.

Решение

Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.

Аналогично:

Получим результат:

Ответ: См. выше.

Задача на вычисление КПД теплового двигателя №5

Условие

Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.

Решение

Запишем формулу для КПД:

Отсюда:

Ответ: 18%

Вопросы на тему тепловые двигатели

Вопрос 1. Что такое тепловой двигатель?

Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.

Вопрос 2. Приведите примеры тепловых двигателей.

Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:

• ракетный двигатель;
• авиационный двигатель;
• газовая турбина.

Вопрос 3. Может ли КПД двигателя быть равен единице?

Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.

КПД реальных двигателей редко превышает 30%.

Вопрос 4. Что такое КПД?

Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.

Вопрос 5. Что такое удельная теплота сгорания топлива?

Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.

Задачи и вопросы на цикл Карно

Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.

Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).

Задача на цикл Карно №1

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.

Решение

Рассчитаем КПД цикла: 

С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:

Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:

Ответ: 0,36; 204,1 кДж; 130,6 кДж.

Задача на цикл Карно №2

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.

Решение

Формула для КПД цикла Карно:

Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:

Ответ: 17%.

Задача на цикл Карно №3

Условие

Изобразите цикл Карно на диаграмме и опишите его

Решение

Цикл Карно на диаграмме PV выглядит следующим образом:

• 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
• 2-3. Адиабатическое расширение, тепло не подводится;
• 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
• 4-1. Адиабатическое сжатие.

Ответ: см. выше.

Вопрос на цикл Карно №1

Сформулируйте первую теорему Карно

Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.

Вопрос на цикл Карно №2

Может ли коэффициент полезного действия в цикле Карно быть равным 100%?

Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.

Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.

Определение

Тепловые машины — устройства, в которых за счет внутренней энергии топлива совершается механическая работа. Чтобы тепловая машина работала циклически, необходимо, чтобы часть энергии, полученной от нагревателя, она отдавала холодильнику.

Второе начало термодинамики

В циклически действующем тепловом двигателе невозможно преобразовать все количество теплоты, полученное от нагревателя, в механическую работу.

В тепловых машинах тепловые процессы замыкаются в цикле Карно. Так называют цикл, или идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В цикле Карно термодинамическая система выполняет механическую работу за счет обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры.

На графике цикл Карно представляется как две адиабаты и две изотермы:

• 1–2 — изотермическое расширение;
• 2–3 — адиабатное расширение;
• 3–4 — изотермическое сжатие;
• 4–1 — адиабатное сжатие.

КПД тепловой машины

Максимальный КПД соответствует циклу Карно.

Второе начало термодинамики

η=Qн−QхQн100%=Qн−PхtQн100%

Преобразовывая формулу, получим:

η=A‘Qн100%

η=NtQн100%

η=A‘A‘+Qх100%

η=Tн−TхTн100%

1. Q_н (Дж) — количество теплоты, полученное от нагревателя (полученное количество теплоты);
2. Q_х (Дж) — количество теплоты, отданное холодильнику (отданное количество теплоты);
3. A’ (Дж) — работа, совершенная газом;
4. N (Вт) — полезная мощность;
5. t (с) — время;
6. T_н (К) — температура нагревателя;
7. T_х (К) — температура холодильника.

Важно! Температуру следует выражать только в кельвинах (К) и КПД не бывает больше 100%.

Алгоритм решения задач на определение КПД теплового процесса

Рассмотрим решение на примере конкретной задачи:

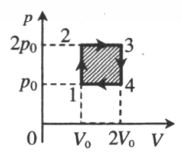
На p-V-диаграмме изображен цикл, проводимый с одноатомным идеальным газом. Определите КПД этого цикла.

• Определить работу газа.

Если тепловой процесс представлен в осях (p, V), то можно определить работу, вычислив площадь фигуры, ограниченной замкнутым циклом:

A‘=p0V0

Если тепловой процесс представлен в других осях координат, то сначала следует его перестроить в осях (p, V) и только потом определять работу.

• Выяснить, на каких этапах повышается температура газа. Именно здесь газ получает энергию:

1–2: V = const, давление увеличивается, температура увеличивается.

2–3: p = const, объем увеличивается, температура увеличивается.

3–4: V = const, давление понижается, температура понижается.

4–1: p = const, объем уменьшается, температура уменьшается.

Отсюда следует, что газ получает энергию только на первом и втором этапах.

• Определить с помощью первого начала термодинамики количество теплоты, полученное газом:

1–2: V = const, A₁₂’ = 0,

Q12=ΔU12=32ΔpV=32Δp0V0=1,5p0V0

1–2: p = const,

ΔU23=Q23−A23; 

ΔU23=32ΔpV=322Δp0V0=3p0V0

A23=pΔV=2p0V0

Q23=3p0V0+2p0V0=5p0V0

Общее количество теплоты:

Qполуч=Q12+Q23=6,5p0V0

• Вычислить КПД, используя основную формулу:

η=A‘Qполуч100%

η=p0V06,5p0V0100%=15,4%

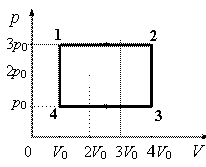
Задание EF17648

За цикл, показанный на рисунке, газ получает от нагревателя количество теплоты Q_нагр = 5,1кДж. КПД цикла равен 4/17. Масса газа постоянна. На участке 1–2 газ совершает работу

Ответ:

а) 1,2 кДж

б) 1,8 кДж

в) 2,6 кДж

г) 3,9 кДж

---

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Определить работу газа на заданном участке.

3.Выполнить решение в общем виде.

4.Выполнить вычисления, подставив известные данные.

Решение

Запишем исходные данные:

• Количество теплоты, переданное газу от нагревателя: Q_нагр = 5,1 кДж.

• Масса постоянна: m = const.

5,1 кДж = 5,1∙10³ Дж

Согласно графику, на участке 1–2 газ совершает работу, равную:

A=3p0(4V0−V0)=9p0V0

Полезная работа ограничивается площадью фигуры внутри циклического графика. Она равна:

Aползн=9p0V0−p0(4V0−V0)=6p0V0

Отсюда:

A=9Aползн6

КПД тепловой машины есть отношение полезной работы к количеству теплоты, полученному от нагревателя:

η=AползнQ

Отсюда:

Aползн=ηQ

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18295

Температура нагревателя идеального теплового двигателя, работающего по циклу Карно, равна T₁, а температура холодильника равна T₂. За цикл двигатель получает от нагревателя количество теплоты Q₁. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

---

Алгоритм решения

1.Определить, от чего зависит КПД двигателя. Выбрать верную формулу.

2.Определить, как вычисляется работа, совершаемая за цикл. Выбрать верную формулу.

Решение

КПД двигателя определяется отношением разности температур нагревателя и холодильника к температуре нагревателя:

η=T1−T2T1=1−T2T1

Верный ответ для «А» — 1.

Работа, совершаемая за цикл, определяется произведением КПД на количество теплоты, полученного от нагревателя:

A=Qη=Q(T1−T2T1)

Верный ответ для «Б» — 2.

Ответ: 12

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18994

Рабочее тело идеальной тепловой машины с КПД, равным 0,25, за цикл своей работы получает от нагревателя количество теплоты, равное 8 Дж. Какова работа, совершаемая за цикл этой машиной?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу КПД тепловой машины.

3.Записать решение в общем виде.

4.Выполнить вычисление искомой величины.

Решение

Запишем исходные данные:

• КПД тепловой машины: η = 0,25.

• Количество теплоты, полученное газом от нагревателя за цикл: Q = 8 Дж.

Формула КПД тепловой машины:

η=AQ

Отсюда:

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 4.6k

Спрятать решение

Спрятать критерии

142

ЛЕКЦИЯ 13

ТЕПЛОВЫЕ МАШИНЫ

13.1. Обратимые и
необратимые процессы

Круговой процесс
– процесс, при котором система, пройдя
через ряд состояний, возвращается в
исходное состояние. На диаграмме
состояний цикл изображается замкнутой
кривой.

Прямой цикл
– это цикл, за который совершается
положительная работа:
.
Цикл протекает по часовой стрелке.

Цикл, совершаемый
идеальным газом можно разбить на процессы
расширения и сжатия. Работа расширения
()
определяется площадью фигуры


положительная ().

Работа сжатия ()
определяется площадью фигуры


отрицательная ().

Работа, совершаемая
газом за цикл, определяется площадью,
охватываемой замкнутой кривой.

Обратный цикл
– цикл, за который совершается
отрицательная работа
.
Цикл протекает против часовой стрелки.

Работа расширения
1а2
положительная
.
Работа сжатия 2b1
отрицательна
.
Работа, совершаемая газом за цикл,
определяется площадью, охватываемой
замкнутой кривой.

Коэффициент
полезного действия (КПД) для кругового
процесса. В
результате кругового процесса система
возвращается в исходное состояние, т.е.
изменение внутренней энергии газа равно
нулю. Запишем первое начало термодинамики:
.
Так как
,
следовательно
,
т.е. работа, совершаемая за цикл, равна
количеству полученной извне теплоты.
Но в результате кругового процесса
система может теплоту как получать, так
и отдавать, тогда

,

где


количество теплоты, полученное о
нагревателя, а


количество теплоты, отданное системой
охладителю.

КПД для кругового
процесса:

.

Процесс называется
обратимым,
если он может происходить как в прямом,
так и в обратном направлении, и система
возвращается в исходное состояние, т.е.
в окружающей среде и в системе не
возникает никаких изменений. Всякий
иной процесс называется необратимым.

Все реальные
процессы сопровождаются диссипацией
энергии (из-за трения, теплопроводности).
Таким образом, обратные процессы – это
идеализированные реальные процессы.
Они более экономичные и имеют максимальный
КПД. Мы их рассматриваем по двум причинам:
1) многие процессы в природе и технике
практически обратимы; 2) можно увидеть
пути повышения КПД реальных двигателей.

Круговые процессы
лежат в основе работы тепловых двигателей
и холодильных машин.

13.2. Тепловые
двигатели и холодильные машины

Тепловой двигатель
‑ это периодически действующий
двигатель, совершающий работу за счет
полученной извне теплоты. В тепловых
двигателях используют прямой цикл.

Принцип действия
теплового двигателя.
От термостата с более высокой температурой
,
называемого нагревателем,
за цикл отнимается количество теплоты
,
а термостату с более низкой температурой
,
называемому холодильником, за цикл
передается количество теплоты
,
при этом совершается работа

(рис. 13.1).

Рис. 13.1 Тепловая
машина

КПД теплового
двигателя ‑ это отношение работы А,
совершаемой двигателем, к затраченной
энергии, т.е. к количеству теплоты, взятой
от нагревателя:

.

Из этого выражения
видно, что даже у идеального теплового
двигателя КПД меньше 1, т.е. меньше 100 %.
Карно показал, что для работы теплового
двигателя необходимо не менее двух
источников теплоты с различными
температурами, т.к. в процессе сжатия
нужно охлаждать рабочее тело. В противном
случае никакой работы совершаться не
будет.

Теорема Карно.
Из всех периодических действующих
тепловых машин, имеющих одинаковые
температуры нагревателей ()
и холодильников (),
наибольшим КПД обладают обратимые
машины. При этом, КПД обратимых машин,
работающих при одинаковых температурах
нагревателей ()
и холодильников (),
равны друг другу и не зависят от природы
рабочего тела (тела, совершающего
круговой процесс и обменивающейся
энергией с другими телами), а определяется
только температурами нагревателя и
холодильника.

.

Холодильные
машины ‑
периодически действующие установки, в
которых за счет работы внешних сил,
теплота переносится к телу с более
высокой температурой.

Принцип действия
холодильных машин.
Системой за цикл от термостата с более
низкой температурой

отнимается количество теплоты

и отдается термостату с более высокой
температурой

количество теплоты

(рис. 13.2).

Рис. 13.2. Холодильная
машина

Поскольку этот
процесс неестественен (теплота не может
самопроизвольно переходить от холодного
тела к горячему) приходится над системой
совершить работу.

.

Таким образом,
количество теплоты Q₁,
отданное системой термостату с более
высокой температурой Т₁,
больше теплоты Q₂,
полученной от термостата с более низкой
температурой Т₂,
на величину работы А,
совершенной над системой.

КПД холодильной
машины (холодильный коэффициент):

.

Вывод:
холодильный коэффициент характеризует
эффективность холодильной машины и
определяется как отношение отнятой от
термостата с более низкой температурой
количества теплоты

к работе А,
которая затрачивается на приведение
холодильной машины в действие. Без
совершения работы нельзя отбирать
теплоту от менее нагретого тела и
передавать ее более нагретому телу.

13.3 Цикл Карно и
работа за цикл

Цикл Карно наиболее
экономичный обратимый круговой цикл,
состоящий из двух изотерм и двух адиабат.
Рассмотрим прямой цикл Карно с идеальным
газом в качестве рабочего тела (рис.
13.3).

Рис. 13.3. Цикл Карно
в диаграмме P,
V

Процесс 1-2
изотермическое расширение; процесс 2-3
адиабатное расширение; процесс 3-4
изотермическое сжатие; процесс 4-1
адиабатное сжатие.

1-2
2-3 3-4
4-1

изотермическое
адиабатное изотермическое
адиабатное

расширение
расширение сжатие сжатие

Рассмотрим
термодинамические процессы и работу в
них.

 изотермическое
расширение
,
,
;

 адиабатное
расширение
,
,
;


изотермическое сжатие
,
,
;


адиабатное сжатие
,
,
.

Работа за цикл:

.

Вывод:
работа за цикл определяется площадью,
ограниченной изотермами и адиабатами
цикла Карно.

Термический КПД
цикла Карно:

.

Используем рис.
13.3 и запишем уравнение адиабатического
процесса в виде
:

;

;

.

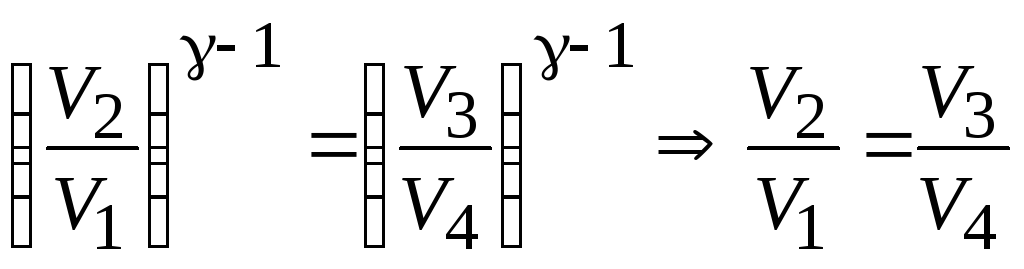
Подставим эти
выражения в формулу для термического
КПД кругового процесса:

.

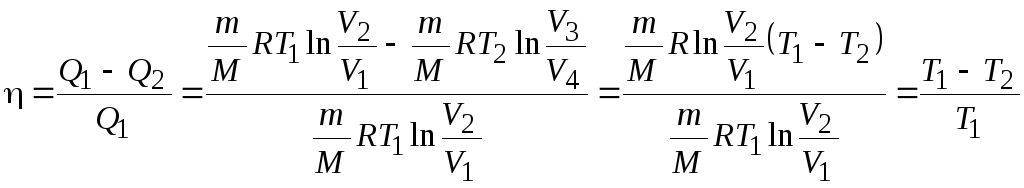
Вывод:
для цикла Карно КПД действительно
определяется только температурами
нагревателя и холодильника.

Контрольные
вопросы

1. Что такое круговой
   процесс?

2. Что такое прямой
   и обратный цикл? Где они применяются?

3. Что такое тепловые
   двигатели и каков принцип их действия?

4. Что такое холодильные
   машины и каков принцип их действия?

5. Что собой
   представляет цикл Карно? Чему равна
   работа за цикл?

6. Получите выражение
   для термического коэффициента полезного
   действия цикла Карно.

Задачи

1. Идеальный тепловой
   двигатель, работающий по циклу Карно,
   совершает за цикл работу 2,94 кДж и отдает
   охладителю количество теплоты 13,4 кДж.
   Найдите КПД цикла. [≈ 18 %].

2. Идеальный тепловой
   двигатель работает по циклу Карно. При
   этом 80% количества теплоты, получаемого
   от нагревателя, передается холодильнику.
   Количество теплоты, полученное от
   нагревателя, 6,28 кДж. Найдите КПД цикла
   и работу, совершаемую за цикл. [0,2;
   ≈ 1,26 кДж].

3. Холодильник,
   работающий по обратному циклу Карно,
   совершает за цикл работу 37 кДж. При этом
   он отбирает тепло от тела отела с
   температурой ‑10 С
   и передает тепло телу с температурой
   17 С.
   Найти холодильный коэффициент
   холодильника и количество теплоты,
   отнятое у холодного тела за цикл. [≈
   9,74; 360 кДж].

ЛЕКЦИЯ 14

ЭНТРОПИЯ. ВТОРОЕ
НАЧАЛО ТЕРМОДИНАМИКИ

14.1. Энтропия и
ее изменение при некоторых термодинамических
процессах

Качественное
отличие теплового движения молекул от
других форм движения ‑ его
беспорядочность, хаотичность. Поэтому
для описания теплового движения молекул
вводят количественную меру степени
молекулярного беспорядка – энтропию.

Соседние файлы в папке 432_lecfiz

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #