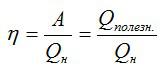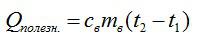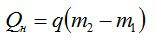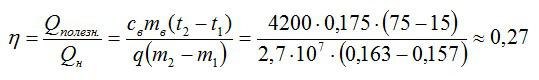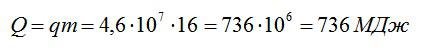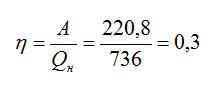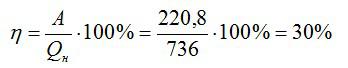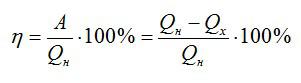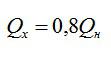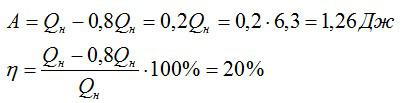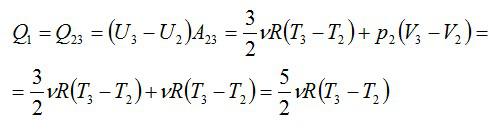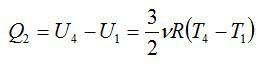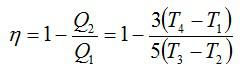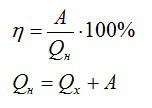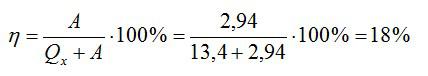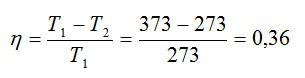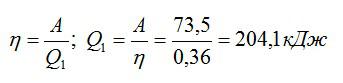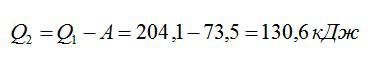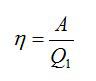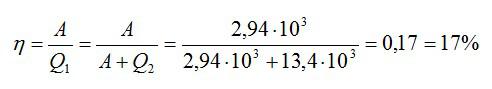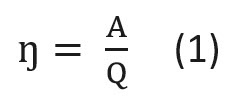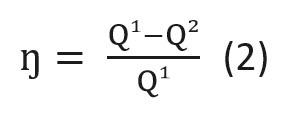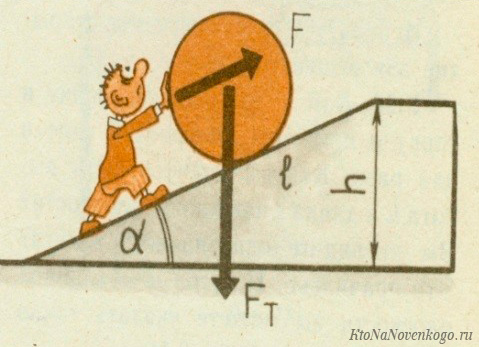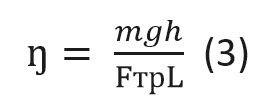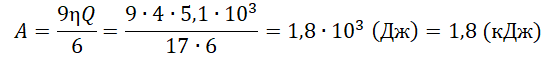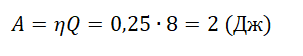Как найти кпд зная теплоту

У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.

Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.

Задачи по физике на КПД теплового двигателя

Задача на вычисление КПД теплового двигателя №1

Условие 

Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.

Решение

Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:

Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:

Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.

Подставляем значения и вычисляем:

Ответ: 27%

Задача на вычисление КПД теплового двигателя №2

Условие

Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.

Решение

Найдем общее количество теплоты, которое произвел двигатель:

Теперь можно рассчитать КПД:

Или, умножая на 100, получаем значение КПД в процентах:

Ответ: 30%.

Задача на вычисление КПД теплового двигателя №3

Условие

Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.

Решение

КПД идеальной тепловой машины:

По условию:

Вычислим сначала работу, а затем КПД:

Ответ: 20%; 1,26 Дж.

Задача на вычисление КПД теплового двигателя №4

Условие

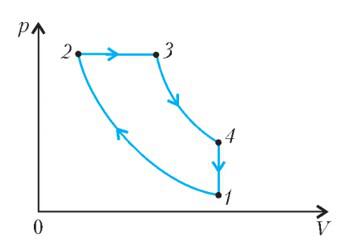
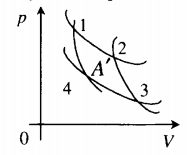
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.

Решение

Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.

Аналогично:

Получим результат:

Ответ: См. выше.

Задача на вычисление КПД теплового двигателя №5

Условие

Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.

Решение

Запишем формулу для КПД:

Отсюда:

Ответ: 18%

Вопросы на тему тепловые двигатели

Вопрос 1. Что такое тепловой двигатель?

Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.

Вопрос 2. Приведите примеры тепловых двигателей.

Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:

• ракетный двигатель;
• авиационный двигатель;
• газовая турбина.

Вопрос 3. Может ли КПД двигателя быть равен единице?

Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.

КПД реальных двигателей редко превышает 30%.

Вопрос 4. Что такое КПД?

Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.

Вопрос 5. Что такое удельная теплота сгорания топлива?

Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.

Задачи и вопросы на цикл Карно

Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.

Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).

Задача на цикл Карно №1

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.

Решение

Рассчитаем КПД цикла: 

С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:

Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:

Ответ: 0,36; 204,1 кДж; 130,6 кДж.

Задача на цикл Карно №2

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.

Решение

Формула для КПД цикла Карно:

Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:

Ответ: 17%.

Задача на цикл Карно №3

Условие

Изобразите цикл Карно на диаграмме и опишите его

Решение

Цикл Карно на диаграмме PV выглядит следующим образом:

• 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
• 2-3. Адиабатическое расширение, тепло не подводится;
• 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
• 4-1. Адиабатическое сжатие.

Ответ: см. выше.

Вопрос на цикл Карно №1

Сформулируйте первую теорему Карно

Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.

Вопрос на цикл Карно №2

Может ли коэффициент полезного действия в цикле Карно быть равным 100%?

Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.

Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.

Вычисление полезной работы через КПД

Измерять КПД принято в процентах. Например, КПД 35%, означает, что почти две трети энергии пошли на ненужные траты, стали рассеянным в пустую теплом, были потрачены на истирание деталей машины, образование искр и т. п.

Важно. 35% совсем не плохой КПД. У паровозов первой половины 20 века он составлял всего 10%. Лишь одна десятая образующегося при сгорании топлива тепла шла на перемещение состава, остальное рассеивалось в атмосфере. Среднеэксплуатационный КПД у современных тепловозов 20-22%. КПД машин на бензиновом ДВС равен 25%. КПД дизеля – 33%. Хорошо на этом фоне выглядит КПД электромобилей. Он у них около 90%.

В формуле нахождения полезной работы да в физике в основном КПД обозначают буквой из греческого алфавита η (эта).

Полезная работа в физике и ненужные траты энергии

Прежде чем говорить о том, как найти полезную работу в физике, следует сказать о ней самой. Дело в том что полезная работа в физике – величина очень даже субъективная. Она напрямую связана с человеческим восприятием, с тем, чего нам нужно получить от системы. Поэтому часто, когда говорят о КПД, имеют в виду различные технические устройства, а не природные объекты.

Хотя технологии постоянно развиваются избежать значительных потерь энергии всё же не удаётся. Получается, что:

Aзатр > Aполез

Aзатр – затраченная работа, Aполез – полезная работа, та что идёт на осуществление нужного нам процесса.

Как бы мы ни пытались уменьшить ненужные потери энергии, полностью от них избавиться не получиться. Непреодолимой преградой для этого является первый закон термодинамики. Из него явственно следует, что КПД любого устройства и механизма ни при каких обстоятельствах не может быть больше единицы и даже стать равным ей.

Мощность представляет собой работу, совершённую за единицу времени. В связи с этим КПД можно посчитать как отношение входной мощности системы к выходной. Т. е.

η = Pвх/Pвых.

Как найти полезную работу в физике используя формулы для разных физических процессов

Вид формул, как найти полезную работу в физике, зависит от природы физических явлений, использующихся для преобразования затраченной энергии в нужную.

Как найти полезную работу в физике механической системы

Лучше всего это показать на конкретном примере. Допустим, нам требуется найти КПД процесса, при котором мальчик вкатывает санки весом 4 кг на горку длиной 12, высотой 2 м. Он прикладывает для этого силу, равную 15 Н.

Решение:

Напомним, что общая формула для КПД

η = (Aполез/Aзатр) * 100%

Aполез в нашем случае равна потенциальной энергии (Eп), которую нужно потратить на то, чтобы поднять санки на высоту, т. е.  Aполез = m*g*h.

Затраченная мальчиком работа равна произведению силы на перемещение, т. е. Aзатр = F*S.

Подставляем в общую формулу для КПД

η = (m*g*h*100)/(F*S)

При подстановке численных значений получаем

η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %

Из этого примера ясно, чему равна полезная работа в физике механической системы, выраженная через КПД.

Формула полезной работы в физике термодинамической системы

Именно по ней судят об эффективности тепловых машин. Допустим, нам нужно отыскать КПД тепловой машины, рабочее тело которой берёт от нагревателя 20кДж, а холодильнику отдаёт 10кДж.

Решение:

Тепловая машина работает следующим образом: нагреватель передаёт определённое количество теплоты рабочему телу, оно из-за этого расширяется, совершая тем самым механическую работу. Однако в последнюю переходит далеко не вся часть переданной тепловой энергии. Чтобы вернуть систему в исходное состояние и начать новый цикл приходится использовать холодильник.

Из выше сказанного можно сделать вывод, что Aполез равна разности энергии взятой от нагревателя и энергии, забранной холодильником, т. е.

Aполез = Qнагревателя – Qхолодильника

Затраченная работа равняется количеству той теплоты, которая была сообщена нагревателю.

Если всё это подставим в формулу для КПД, то получим

[eta=(text { Qнагревателя }-text { Qхолодильника })^{*} 100 / text { Qнагревателя }]

После подстановки численных значений будем иметь

η = (20 – 10)/20*100% = 50%

Теперь ясно, как определить полезную работу в физике термодинамической системы.

Формула полезной работы в физике электродинамической системы

Очень важный класс явлений. Каждый день все пользуются самыми разными электрическими устройствами: телевизором, компьютером, телефоном и т. д. Но мы рассмотрим случай попроще. Вычислим КПД электрического чайника. Допустим воде было передано 22176 Дж тепла за 2 мин. Напряжение в электросети стандартное 220 В. Сила тока равняется 1,4 А.

Решение:

Aполез будем считать работу, которая пошла на нагрев воды. Хотя она нам и дана из условия, формулу вспомнить всё равно не будет лишним.

• Q = cm(tконечная-tначальная)
• Q — количество теплоты [Дж]
• c — удельная теплоёмкость вещества [Дж/кг*˚C]
• m — масса [кг]
• tконечная — конечная температура [˚C]
• tначальная — начальная температура [˚C]
• Работа тока вычисляется по формуле
• A = (I^2)*Rt = (U^2)/R *t = UIt
• A — работа электрического тока [Дж]
• I — сила тока [А]
• U — напряжение [В]
• R — сопротивление [Ом]
• t — время [c]

В нашем примере она примет вид

η = Q/A *100% = Q/UIt *100%

Переводим минуты в секунды и, подставляя численные значения, получаем

η = 22176/220*1,4*120 *100% = 60%

Формула полезной работы электродинамической системы будет:

Формула КПД и как его вычислить для тепловой машины или механизма

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта аббревиатура вряд ли требует расшифровки: она неизвестна разве что тем, у кого в школе был «неуд» по физике.

Но для забывчивых всё же напомним, что под этим сокращением скрывается коэффициент полезного действия. Что же собой представляет эта величина?

Поговорим о ней простым и понятным языком – это может пригодиться даже в повседневной жизни.

Что такое КПД в физике и какова его формула

Для выполнения какой-либо работы необходимо затратить определённое количество энергии. Чтобы ехал велосипед, вы тратите мышечную энергию крутя педали. Чтобы двигался автомобиль, используется энергия сжигаемого топлива (бензина, солярки или газа).

Для горения лампочки требуется энергия электрического тока. Список можно продолжать до бесконечности. Точку можно поставить на солнечной энергии, благодаря которой существует жизнь на Земле.

Далее возникает логичный вопрос: а насколько эффективно расходуется эта энергия? В идеале хотелось бы, чтобы вся она шла «в дело», то есть использовалась только по прямому назначению. Но, к сожалению, на практике такого не бывает.

Затраченная энергия будет всегда больше, чем полезная работа, так как для достижения основной цели (движение, подъём груза, освещение, отопление и т.д.) часть энергии неизбежно уйдёт на неустранимые потери (преодоление силы трения, нагрев электропроводки, выброс продуктов горения в атмосферу и т.д.). Понятно, что чем меньше такие потери, тем лучше.

Критерием того, насколько эффективно работает система (устройство, агрегат, двигатель, машина и т.д.), служит показатель, получивший название коэффициент полезного действия (КПД).

Иными словами, коэффициент полезного действия показывает, какова доля полезной работы в общих энергозатратах. Математически КПД (чаще всего обозначается символом ŋ) определяется по формуле:

где A — полезная энергия (работа);
Q — энергия, затраченная на совершение полезной работы.

Понятно, что ŋ – величина безразмерная и не может быть больше единицы (да и равной единице она может быть чисто теоретически).

Выражается она в виде десятичной дроби либо в процентах (в последнем случае в формулу вставляется множитель х100).

Так, если КПД равен 0,9 (90%), то это значит, что 10% полезной мощности составили безвозвратные потери.

КПД теплового двигателя (машины)

Под тепловым двигателем понимается машина (агрегат), в которой энергия, высвобождающаяся в процессе расширения рабочего тела, преобразуется в механическую работу.

В качестве рабочего тела обычно выступает газ или газообразные вещества (пары бензина, водяной пар и т.п.).

Тепловые машины работают по замкнутому циклу. Это значит, что процесс преобразования энергии и сопутствующей теплопередачи периодически повторяется, а рабочее тело совершает круговой цикл, возвращаясь в исходное состояние.

К тепловым двигателям относятся:

1. поршневые (паровые машины, двигатели внутреннего сгорания);
2. роторные/турбинные (газовые или паровые турбины АЭС и ТЭЦ);
3. реактивные (авиация);
4. ракетные (космическая техника).

Используя положения предыдущего параграфа, КПД тепловой машины можно сформулировать как отношение полезной работы, совершённой за один цикл, к энергии (количеству теплоты), поступившей от энергоносителя (нагревателя).

Тогда формулу (1) можно преобразовать следующим образом:

где Q1 — количество теплоты, полученное двигателем от нагревателя за цикл;
Q2 — количество теплоты, отданное двигателем охладителю (холодильнику) за цикл;
Q1 – Q2 – количество теплоты, которое пошло на совершение работы.

Предположим, что Q1 = Q2, то есть на совершение полезной работы ничего не осталось – вся энергия «ушла в трубу». Тогда и КПД будет нулевым. Если же Q2 = 0, то есть вся энергия отдана полезной работе (потери отсутствуют), то коэффициент полезного действия будет равен 1.

Но это теория, на практике ни то ни другое нереалистично. В первом случае двигатель просто бесполезен, во втором – идеален, но недосягаем.

Значения КПД для различных типов тепловых двигателей приведены ниже.

Самым большим КПД обладают тепловые двигатели, работающие на основе цикла Карно (процесс назван в честь французского инженера, открывшего это явление в 1824 г.). В термодинамике оно характеризует круговой цикл, включающий в себя две стадии: расширение и сжатие рабочего тела.

Причём на протяжении обеих стадий попеременно проходят два процесса: изотермический (протекающий при постоянной температуре), и адиабатический (протекающий без теплообмена с окружающей средой). Максимальное значение КПД здесь достигается за счёт того, что тела с разной температурой не контактируют, а значит, без осуществления работы теплопередача исключается.

КПД механизма — по какой формуле вычисляют

Человек придумал разнообразные механизмы, с помощью которых можно поднимать тяжёлые грузы на определённую высоту. Так, для подъёма ведра с водой из колодца изобрели ворот, для подъёма автомобиля – домкрат. При помощи лебёдки и наклонной плоскости египтяне построили свои грандиозные пирамиды.

Пользуясь этими приспособлениями, человек редко вспоминает об их КПД. В качестве примера рассмотрим этот показатель для наклонной плоскости.

Принцип расчёта КПД остаётся неизменным: нужно найти отношение полезной работы ко всей затраченной энергии. То есть опять-таки используем общую формулу (1), сделав соответствующие преобразования.

Предположим, тело массой m нужно поднять (точнее затолкать или затянуть) на высоту h. При постоянной скорости подъёма полезная работа будет равна произведению силы тяжести (mg) на высоту (h).

Затраченная работа определяется произволением силы толчка или тяги F на длину наклонной плоскости L. Заметим, что толчковое (тяговое) усилие идёт на преодоление силы трения Fтр.

Таким образом, КПД такого простейшего механизма можно посчитать по формуле:

Несложный анализ показывает, что коэффициент полезного действия наклонной плоскости обратно пропорционален силе трения и длине аппарели. Последняя, в свою очередь, зависит от угла наклона: чем он больше, тем короче аппарель.

Как можно увеличить КПД

Современная наука постоянно ищет пути повышения коэффициента полезной модности двигателей и отдельных механизмов, внедряя новые технические решения и технологические инновации.

Чем выше будет КПД, тем экономичней будет двигатель, тем больше энергоресурсов удастся сберечь.

Тепловой двигатель

Из формулы (2) следует, что для увеличения КПД есть два пути: а) повышение температуры нагревателя; б) понижение температуры холодильника. Оба пути малоперспективны.

Нагреватель нельзя разогревать до бесконечности, так как любой материал имеет предел жаропрочности. Холодильником почти всегда служит окружающая среда, а внедрение в систему дополнительного теплообменника (например, баллона с жидким азотом) нецелесообразно: это резко увеличит вес, габариты и стоимость двигателя.

Установлено, что на коэффициент полезного действия не влияют характеристики рабочего тела. Что же остаётся?

А остаётся немало практически реализуемых способов, таких как уменьшение трения в механических узлах, минимизация теплопотерь путём достижения максимально полного сгорания топлива, создание обтекаемых форм для снижения лобового сопоставления (воздуха или воды) и т.д.

Учитывая, что в механике хорошим показателем на сегодняшний день считается КПД 30-40%, учёным и практикам есть над чем работать.

Наклонная плоскость

Из формулы (3) следует, что для повышения КПД нужно снижать силу трения (прежде всего, путём создания гладких соприкасающихся поверхностей) и увеличивать угол наклона. Но! При крутом уклоне силёнок для поднятия тяжёлого груза может и не хватить.

В заключение отметим, что в электротехнике ситуация с КПД обстоит гораздо лучше (показатель в 95% для электродвигателя – норма). На то есть объективные причины, объяснение которых выходит за рамки рассматриваемой темы.

Определение

Тепловые машины — устройства, в которых за счет внутренней энергии топлива совершается механическая работа. Чтобы тепловая машина работала циклически, необходимо, чтобы часть энергии, полученной от нагревателя, она отдавала холодильнику.

Второе начало термодинамики

В циклически действующем тепловом двигателе невозможно преобразовать все количество теплоты, полученное от нагревателя, в механическую работу.

В тепловых машинах тепловые процессы замыкаются в цикле Карно. Так называют цикл, или идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В цикле Карно термодинамическая система выполняет механическую работу за счет обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры.

На графике цикл Карно представляется как две адиабаты и две изотермы:

• 1–2 — изотермическое расширение;
• 2–3 — адиабатное расширение;
• 3–4 — изотермическое сжатие;
• 4–1 — адиабатное сжатие.

КПД тепловой машины

Максимальный КПД соответствует циклу Карно.

Второе начало термодинамики

η=Qн−QхQн100%=Qн−PхtQн100%

Преобразовывая формулу, получим:

η=A‘Qн100%

η=NtQн100%

η=A‘A‘+Qх100%

η=Tн−TхTн100%

1. Q_н (Дж) — количество теплоты, полученное от нагревателя (полученное количество теплоты);
2. Q_х (Дж) — количество теплоты, отданное холодильнику (отданное количество теплоты);
3. A’ (Дж) — работа, совершенная газом;
4. N (Вт) — полезная мощность;
5. t (с) — время;
6. T_н (К) — температура нагревателя;
7. T_х (К) — температура холодильника.

Важно! Температуру следует выражать только в кельвинах (К) и КПД не бывает больше 100%.

Алгоритм решения задач на определение КПД теплового процесса

Рассмотрим решение на примере конкретной задачи:

На p-V-диаграмме изображен цикл, проводимый с одноатомным идеальным газом. Определите КПД этого цикла.

• Определить работу газа.

Если тепловой процесс представлен в осях (p, V), то можно определить работу, вычислив площадь фигуры, ограниченной замкнутым циклом:

A‘=p0V0

Если тепловой процесс представлен в других осях координат, то сначала следует его перестроить в осях (p, V) и только потом определять работу.

• Выяснить, на каких этапах повышается температура газа. Именно здесь газ получает энергию:

1–2: V = const, давление увеличивается, температура увеличивается.

2–3: p = const, объем увеличивается, температура увеличивается.

3–4: V = const, давление понижается, температура понижается.

4–1: p = const, объем уменьшается, температура уменьшается.

Отсюда следует, что газ получает энергию только на первом и втором этапах.

• Определить с помощью первого начала термодинамики количество теплоты, полученное газом:

1–2: V = const, A₁₂’ = 0,

Q12=ΔU12=32ΔpV=32Δp0V0=1,5p0V0

1–2: p = const,

ΔU23=Q23−A23; 

ΔU23=32ΔpV=322Δp0V0=3p0V0

A23=pΔV=2p0V0

Q23=3p0V0+2p0V0=5p0V0

Общее количество теплоты:

Qполуч=Q12+Q23=6,5p0V0

• Вычислить КПД, используя основную формулу:

η=A‘Qполуч100%

η=p0V06,5p0V0100%=15,4%

Задание EF17648

За цикл, показанный на рисунке, газ получает от нагревателя количество теплоты Q_нагр = 5,1кДж. КПД цикла равен 4/17. Масса газа постоянна. На участке 1–2 газ совершает работу

Ответ:

а) 1,2 кДж

б) 1,8 кДж

в) 2,6 кДж

г) 3,9 кДж

---

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Определить работу газа на заданном участке.

3.Выполнить решение в общем виде.

4.Выполнить вычисления, подставив известные данные.

Решение

Запишем исходные данные:

• Количество теплоты, переданное газу от нагревателя: Q_нагр = 5,1 кДж.

• Масса постоянна: m = const.

5,1 кДж = 5,1∙10³ Дж

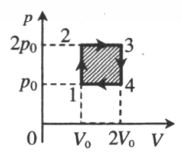
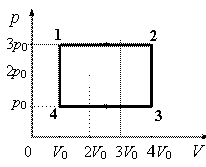
Согласно графику, на участке 1–2 газ совершает работу, равную:

A=3p0(4V0−V0)=9p0V0

Полезная работа ограничивается площадью фигуры внутри циклического графика. Она равна:

Aползн=9p0V0−p0(4V0−V0)=6p0V0

Отсюда:

A=9Aползн6

КПД тепловой машины есть отношение полезной работы к количеству теплоты, полученному от нагревателя:

η=AползнQ

Отсюда:

Aползн=ηQ

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18295

Температура нагревателя идеального теплового двигателя, работающего по циклу Карно, равна T₁, а температура холодильника равна T₂. За цикл двигатель получает от нагревателя количество теплоты Q₁. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

---

Алгоритм решения

1.Определить, от чего зависит КПД двигателя. Выбрать верную формулу.

2.Определить, как вычисляется работа, совершаемая за цикл. Выбрать верную формулу.

Решение

КПД двигателя определяется отношением разности температур нагревателя и холодильника к температуре нагревателя:

η=T1−T2T1=1−T2T1

Верный ответ для «А» — 1.

Работа, совершаемая за цикл, определяется произведением КПД на количество теплоты, полученного от нагревателя:

A=Qη=Q(T1−T2T1)

Верный ответ для «Б» — 2.

Ответ: 12

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18994

Рабочее тело идеальной тепловой машины с КПД, равным 0,25, за цикл своей работы получает от нагревателя количество теплоты, равное 8 Дж. Какова работа, совершаемая за цикл этой машиной?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу КПД тепловой машины.

3.Записать решение в общем виде.

4.Выполнить вычисление искомой величины.

Решение

Запишем исходные данные:

• КПД тепловой машины: η = 0,25.

• Количество теплоты, полученное газом от нагревателя за цикл: Q = 8 Дж.

Формула КПД тепловой машины:

η=AQ

Отсюда:

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 4.6k

Полное условие задачи

Найдите КПД цикла, изображенного на рисунке для идеального одноатомного газа.

Краткое условие задачи

Решение задачи

КПД цикла находим по формуле:

где работа определяется как площадь прямоугольника 1234:

Для определения затраченного количества теплоты нужно выяснить, в каких процессах газ получал теплоту. Для этого воспользуемся первым законом термодинамики, формулой для изменения внутренней энергии и уравнением состояния идеального газа:

Рассмотрим каждый процесс по отдельности.

В процессе 1 – 2 начальная температура меньше конечной:

поэтому изменение внутренней энергии больше нуля:

а работа равна нулю, поскольку процесс изохорный:

Отсюда следует, что газ в процессе 1 – 2 получал тепло:

Найдем это тепло:

Разность температур найдем используя уравнение состояния идеального газа. Запишем его для состояния 1 и для состояния 2:

Вычитаем из второго уравнения первое и находим разность температур:

Подставим в формулу для теплоты:

В процессе 2 – 3 начальная температура также меньше конечной:

поэтому изменение внутренней энергии также больше нуля:

а работа в этом процессе больше нуля (газ совершает работу):

поскольку объем увеличивается:

Отсюда следует, что газ в процессе 2 – 3 тоже получал тепло:

Найдем это тепло:

Разность температур найдем используя уравнение состояния идеального газа. Запишем его для состояния 2 и для состояния 3:

Вычитаем из второго уравнения первое и находим разность температур:

Подставим в формулу для теплоты:

В процессе 3 – 4 начальная температура больше конечной:

поэтому изменение внутренней энергии меньше нуля:

а работа равна нулю, поскольку процесс изохорный:

Отсюда следует, что газ в процессе 3 – 4 отдает тепло:

В процессе 4 – 1 начальная температура также больше конечной:

поэтому изменение внутренней энергии также меньше нуля:

работа в этом процессе тоже меньше нуля (над газом совершают работу):

поскольку объем уменьшается:

Отсюда следует, что газ в процессе 4 – 1 тоже отдает тепло:

Таким образом затраченная теплота равна:

Искомый КПД равен:

Или

Ответ: 17 %.